Верификация компьютерного кода ГРАТ методом Сизых

Верификация программного обеспечения компьютерной модели - это «процесс определения соответствия ПО КМ (компьютерной модели, программы) математической модели. Верификация обеспечивает обоснование того, что ПО КМ при определенных параметрах рассчитывает математическую модель правильно и с соответствующей точностью» (ГОСТ Р 57700.2 - 2017). В условиях отсутствия нетривиальных точных решений для некоторых типов задач аэромеханики верификация соответствующих кодов проводится путем сравнения численных решений с решениями, полученными хорошо зарекомендовавшими себя кодами. Однако в отсутствие точных решений для верификации могут быть использованы свойства, которые должны выполняться на всех точных решениях, например сохранение отношения завихренности к давлению (инвариант Крокко) на линиях тока в плоских стационарных изоэнергетических течениях [1]. В работах [2, 3] предложен новый способ верификации, состоящий в проверке выполнения неизвестных ранее закономерностей, полученных аналитически непосредственно из уравнений соответствующих математических моделей и не заложенных, в отличие от известных законов сохранения, в численные схемы. В частности, предложено использовать неизвестный ранее дозвуковой принцип максимума давления (ДПМД) для стационарных течений идеального газа [3]. В условия этого принципа максимума входит параметр Q (так называемый Q-параметр), который можно записать в виде

Q = 0.5 (ft2 - (Vu)2 - (Vv)2 - (Vw)2} , где u, v и w ~ компоненты скорости V в прямоугольной декартовой системе координат, П = |Q|. Q = rotV.

ДПМД формулируется следующим образом.

Пусть G - ограниченная область дозвукового стационарного течения идеального совершенного газа, в которой давление не постоянно.

Тогда в зависимости от знака Q во всех точках G справедливы три следующих утверждения.

• 1.    Если Q <  0, то давление р достигает на G минимума на границе и только на границе области G.

• 2.    Если Q >  0, то давление р достигает на G максимума на границе и только на границе области G.

• 3.    Если Q = 0, то давление р достигает на G минимума и максимума на границе и только на границе области G.

В серии работ В. В. Вышинского с соавторами [4-10] для верификации дозвуковых расчетов использовалась проверка выполнения следующего следствия ДПМД.

Если давление не постоянно всюду и достигает строгого или нестрогого минимума во внутренней точке течения, то Q-параметр в этой точке должен быть неотрицательным, а во внутренней точке максимума давления Q-параметр должен быть неположительным.

Это следствие ДПМД позволяет для верификации ограничиться вычислением Q- параметра только в точке экстремума давления, вычисляя только первые производные компонент скорости. В упомянутых выше работах [4-10] параметры сетки улучшались (сетка измельчалась и модифицировалась) до тех пор, пока следствие ДПМД не оказывалось выполненным. После этого авторы [4-10] считали свои расчеты удовлетворяющими «критерию независимой верификации» (термин предложен В. В. Вышинским в работе [4]).

Одна из важнейших задач прикладной аэромеханики состоит в вычислении сил, действующих на тело в потоке газа. Поэтому расчет распределения давления по поверхности тела является одной из важнейших задач вычислительной аэромеханики. В этой связи настоящая статья посвящена представлению нового способа верификации и оценки точности кода путем проверки выполнения в расчете одной закономерности, которая наблюдалась в некоторых численных расчетах и в эксперименте [11], но до 2019 года не была обоснована теоретически. Она состоит в том, что при сверхзвуковом обтекании тела вращения энтропия максимальна на поверхности тела при любых углах атаки. В 2019 году для тел с гладкой выпуклой носовой частью, при обтекании которых сверхзвуковым потоком формируется отошедший головной скачок, эта закономерность была теоретически обоснована в [12]. Если осесимметричное тело с гладкой выпуклой носовой частью расположено так, что ось симметрии параллельна скорости набегающего сверхзвукового потока (нулевой угол атаки), то эту закономерность легко объяснить. Действительно, в силу симметрии линия тока АВ, лежащая на оси симметрии (рис. 1а), заканчивается на теле в критической точке В. При этом точка А расположена на скачке там, где касательная к скачку плоскость перпендикулярна скорости набегающего потока. Поэтому параметры течения в критической точке В можно рассчитывать по параметрам набегающего потока. Для этого достаточно использовать условия Ренкина - Гюгонио на прямом скачке в точке А и условие сохранения энтропии на критической линии тока. Согласно условиям Ренкина - Гюгонио для произвольного угла наклона скачка, сразу за скачком энтропия принимает максимальное значение в точке, где угол наклона прямой. Поэтому энтропия принимает максимальное значение на критической линии тока и на поверхности тела.

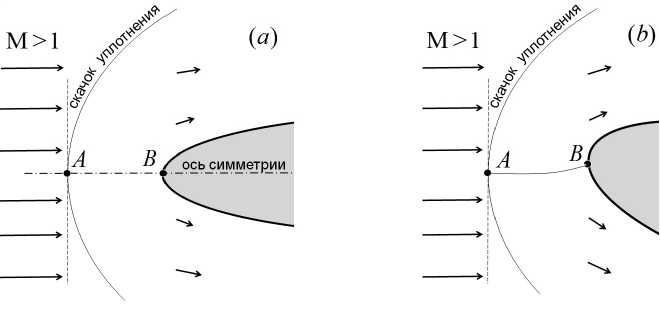
Рис. 1. Гладкая выпуклая носовая часть в сверхзвуковом потоке: (а) - осесимметричное обтекание; (6) - не осесимметричное обтекание [12]

В статье [12] рассмотрен ЗВ-случай, когда есть угол атаки или тело не осесимметрично. Доказано, что, как и в осесимметричном случае, точка А расположена на скачке там, где касательная к скачку плоскость перпендикулярна направлению набегающего потока (рис. 1Ъ). Как следствие, энтропия принимает максимальное значение на критической линии тока и на поверхности тела, а поэтому давление торможения минимально на критической линии тока и на поверхности тела и равно давлению торможения, вычисленному по формулам Рэнкина - Гюгонию для давления торможения Во за прямым скачком через давление Р^ и число Маха М_ю невозмущенного набегающего сверхзвукового потока [13]:

7 +1              — 1

■ ■ = (^ ) ^7—1 (^) ^7—1 м^ В м~ -1)

где у - показатель адиабаты (для воздуха у = 1 . 4).

В настоящей статье проверка выполнения теоретически установленной закономерности [12] используется для верификации кода ГРАТ и оценки точности расчета обтекания тела сверхзвуковым потоком совершенного газа с отошедшим скачком при различных параметрах расчетной сетки.

2.    Физико-математическая постановка задачи

В данном разделе представлено описание физико-математической постановки задачи как примера применения предложенного Г. Б. Сизых подхода к верификации и к оценке точности компьютерного кода ГРАТ, предназначенного для суперкомпьютерного моделирования аэротермогазодинамики высокоскоростных реагирующих течений с сильными ударными волнами [14-16]. В основе данного компьютерного кода лежит численное решение методом конечного объема трехмерной нестационарной системы уравнений движения вязкого, теплопроводного, химически реагирующего газа, дополненной двухпараметрической RANS-моделью турбулентности к — ш SST вида дw ^ 3Fхw । 3Fу w । 3Fz w 3GX w ^ 3Gy w ^ 3GZw где w - столбец консервативных переменных, Fх. Fу. Fz - компоненты вектора конвективного потока, Gx, Gy, Gz - компоненты вектора вязкого потока.

Численное интегрирование системы уравнений газовой динамики проводилось с использованием модифицированного метода AUSM+ [17]. Используемый для численного интегрирования метод AUSM+ является методом расщепления потоков на конвективную и акустическую составляющие в зависимости от числа Маха. Такой подход является альтернативой методам, основанным на идее вычисления потоков через грани конечного объема из решения задачи о распаде произвольного разрыва, предложенной С. К. Годуновым [18]. Для получения более высокого порядка точности численного решения по пространству проводилась процедура линейной реконструкции распределения газодинамических параметров внутри ячейки по неконсервативным переменным. Значения газодинамических параметров, используемые для вычисления потоков через грани конечного объема, определяются на каждой грани из задаваемого распределения, что приводит к схеме второго порядка в областях, где решение гладкое. Но при этом для сохранения свойства монотонности численной схемы на газодинамических разрывах необходимо использовать ограничитель задаваемого распределения. Численное интегрирование системы уравнений газовой динамики проводилось до установления стационарного решения.

На рис. 2 представлена трехмерная поверхность осесимметричного тела, затупленного по эллипсоиду с соотношением 1:2:2, созданная для проведения аэродинамических расчетов.

Рис. 2. Трехмерная модель осесимметричного затупленного тела

Численное моделирование трехмерного поля течения проводилось с использованием неструктурированных сеток, важным преимуществом которых является автоматизация построения для сложных геометрических форм. Расчетная сетка состояла из тетраэдральных и призматических элементов, фрагмент которой представлен на рис. 3.

Для более детального описания поля течения в области отошедшей ударной волны и для исследования влияния подробности расчетной сетки на изменение давления в области точки торможения потока проводилось сгущение призматическими элементами. Сгущение расчетной сетки осуществлялось путем увеличения количества призматических элементов в нормальном направлении к поверхности осесимметричного затупленного тела, что позволило сохранить топологию расчетной сетки для дальнейшего анализа сходимости решения по сетке и оценки величины отклонения рассчитанного давления в точке торможения потока на теле от точного теоретического значения.

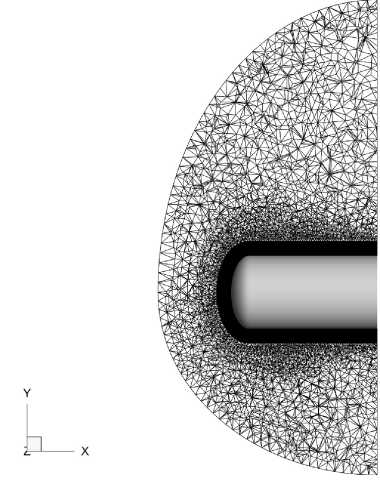
Рис. 3. Фрагмент расчетной сетки в сечении z = 0

Количество призматических ячеек в нормалвном направлении к поверхности осесимметричного затупленного тела задавалосв равным 25, 50 и 100 элементам. В итоге были построены три расчетные сетки разного уровня подробности в области отошедшей ударной волны, представленные на рис. 4.

Рис. 4. Расчетные сетки с возрастающим количеством призматических элементов в нормалвном направлении к поверхности затупленного тела

Общее количество ячеек в расчетной области для сеток составило 1 102 305, 1 774 055 и 3 117 555 элементов.

На поверхности обтекаемого тела задавалисв граничные условия проскальзывания с теплоизолированной поверхностью вследствие того, что обтекание при моделировании осесимметричного затупленного тела проводилось сверхзвуковым потоком невязкого, совершенного газа, вследствие чего компоненты вектора вязкого потока в системе уравнений газовой динамики полагались равными нулю.

3.    Результаты численного моделирования

В данном разделе представлены результаты, полученные при помощи компьютерного кода ГРАТ. На рис. 5-8 представлены распределения давления, полученные на сетках разного уровня подробности в результате численного моделирования невязкого обтекания сверхзвуковым потоком осесимметричного тела затупленного по эллипсоиду для двух чи- сел Маха 3 и 4 под двумя углами атаки: 15 и 30 градусов. Погрешности (отклонения) расчетного значения давления в точке торможения от теоретического значения приведена! в табл. 1 и 2.

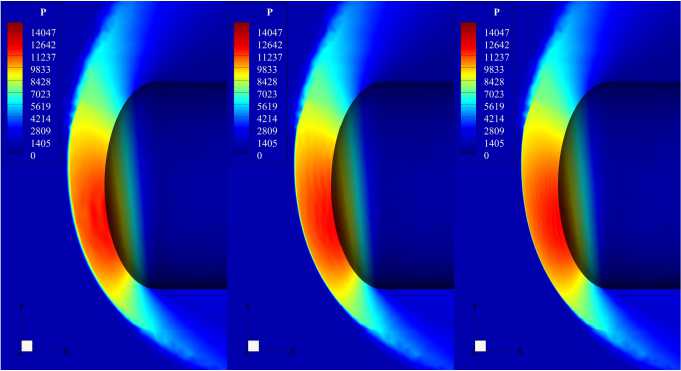
Рис. 5. Распределения давления в окрестности затупленного тела на сетках разного уровня подробности, M = 3, угол атаки а = 15°

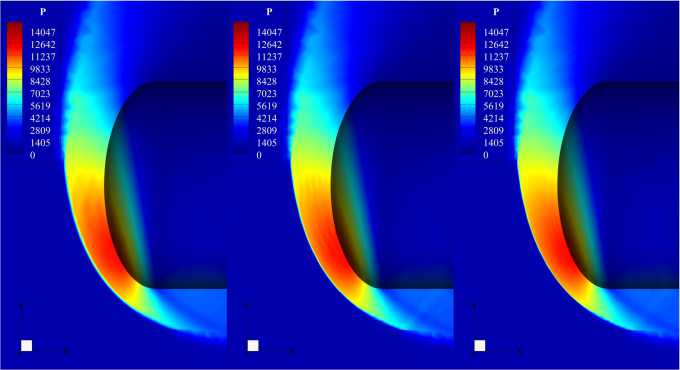
Рис. 6. Распределения давления в окрестности затупленного тела на сетках разного уровня подробности, M = 3, угол атаки а = 30°

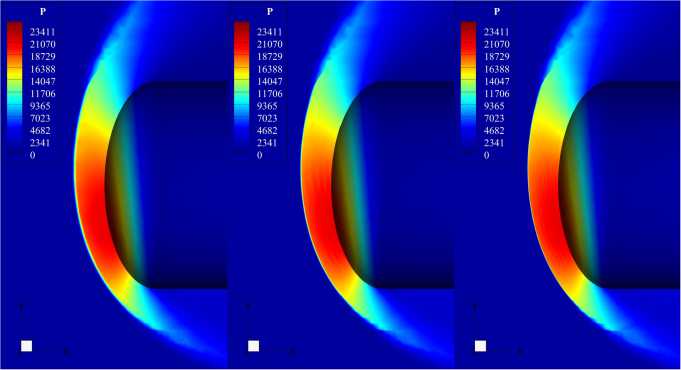
Рис. 7. Распределения давления в окрестности затупленного тела на сетках разного уровня подробности, M = 4, угол атаки а = 15°

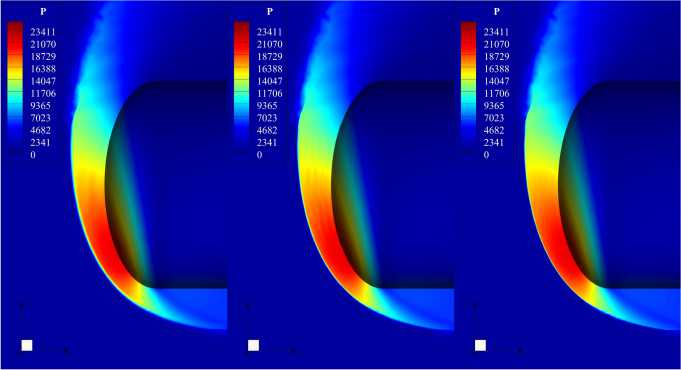
Рис. 8. Распределения давления в окрестности затупленного тела на сетках разного уровня подробности, M = 4, угол атаки a = 30°

Таблица!

Сравнение давления в области точки торможения потока при числе Маха 3 с теоретическим значением полного давления, равного 12 061 Па

Число призматических ячеек в нормальном направлении	Угол атаки 15°		Угол атаки 30°
	Расчетное значение	Погрешность	Расчетное значение	Погрешность
25	12 246 Па	1.53%	11899 Па	1.34%
50	12194 Па	1.10%	11915 Па	1.21%
100	12 060 Па	0.00%	11977 Па	0.70%

Таблица2

Сравнение давления в области точки торможения потока при числе Маха 4 с теоретическим значением полного давления, равного 21 068 Па

Число призматических ячеек в нормальном направлении	Угол атаки 15°		Угол атаки 30°
	Расчетное значение	Погрешность	Расчетное значение	Погрешность
25	20 735 Па	1.58%	20 886 Па	0.86%
50	20 920 Па	0.70%	20 902 Па	0.79%
100	21105 Па	0.18%	21069 Па	0.00%

4.    Заключение

Для верификации компьютерного кода ГРАТ методом Сизых проведены расчеты обтекания под углом атаки сверхзвуковым потоком идеального совершенного газа тела вращения с гладкой выпуклой носовой частью.

В качестве критерия оценки качества кода рассматривалась степень отклонения величины давления на теле в передней точке торможения, полученной в расчетах, от точного значения, которое согласно [12] равно давлению торможения за прямым скачком.

Анализ результатов расчетов, выполненных на сетках с измельчением для двух значений угла атаки и числа Маха, показал тенденцию уменьшения отклонения вычисленного давления от точного по мере измельчения расчетной сетки.

Проведенное исследование дает основание утверждать, что метод Сизых дает возможность провести верификацию и получить объективную количественную оценку точности компьютерного кода.