Верификация математической модели процесса промерзания с уравнением сопряжения на подвижной границе

В классической постановке задачи Стефана [1] на подвижной границе промерзания влажного материала записывают граничное условие четвертого рода (ГУ IV) с источником теплоты или так называемое условие Стефана:

- - - 7 d t  у д t       d ^

tf   tth = tph;   ^ f       ^ th     = Qph , д n д n      dт где tf, th, tph - соответственно температура мерзлой, талой зон влажного грунта и фазового превращения воды в лед, °С; λf, λth соответственно коэффициенты теплопроводности грунта в мерзлой и талой зонах, W/(m-K); n - нормаль к поверхности раздела фаз; £ - координата подвижной границы раздела фаз, м; т - время, с; Qph = qph р W- скрытая теплота фазового превращения влажного грунта, Дж/м3; qph, р, W- соответственно удельная скрытая теплота фазового превращения, Дж/кг, плотность грунта в сухом состоянии, кг/м3, и весовая влажность грунта в долях единицы.

Задача Стефана с ГУ IV рода (1) относится к классу сопряженных задач теплообмена в гетерогенных системах с подвижными и неподвижными границами раздела фаз. Однако существует иной подход к описанию задачи Стефана, суть которого заключается в одинаковом представлении процессов переноса теплоты в сопряженных телах и на границах их раздела. К подобному заключению пришли авторы работ [2–4], объединив уравнение теплопроводности с ГУ IV рода (1). Полученное таким образом обобщенное уравнение теплопроводности с эффективной сглаженной теплоемкостью становится пригодным для описания всей расчетной области. Это позволило в сопряженной задаче теплообмена с фазовыми превращениями вещества на подвижной границе применить метод сквозного счета.

Но к этому заключению о едином математическом описании гетерогенной системы можно прийти прямым путем, непосредственно наблюдая природу процессов переноса теплоты и фазовых превращений вещества. Действительно, теплофизические свойства веществ на границах раздела и внутри взаимодействующих тел по природе своей одинаковы, отличаются друг от друга лишь количественно. Механизмы переноса теплоты в этих телах и на их границах раздела также происходят по одним и тем же законам природы: теплопроводность, конвекция и излучение. Подобное единство свойств веществ и механизмов переноса теплоты предполагает одинаковое формализованное описание процессов теплообмена в виде уравнений энергии, в частном случае теплопроводности [5-7]. При этом в уравнении теплопроводности на подвижной границе, назовем его уравнением сопряжения, для влажного вещества ( W > 0) появится источник теплоты в виде фазовых превращений влаги.

На первом этапе проверки адекватности математической модели в новой постановке реальному процессу нами был проведен вычислительный эксперимент по изучению процесса промерзания влажного грунта [8]. Для сравнения данная задача была реализована в традиционной постановке с ГУ IV (1) с использованием известных численных методов решения: метода ловли фронта в узел сетки (МЛФУС) и метода выпрямления фронтов (МВФ) [4, 9-13]. Срав- нение результатов моделирования в указанных постановках показало их удовлетворительное совпадение между собой и с величиной максимальной глубины сезонного промерзания влажного песчаного грунта в г. Новосибирске1.

Необходимо отметить, что численное решение задачи с уравнением сопряжения на подвижной границе [8] обладает рядом достоинств перед известными методами. Во-первых, модель с уравнением сопряжения позволяет реализовать метод сквозного счета , как в работах [2–4], но в отличие от них в авторской модели представляется возможность явно выделять местоположение подвижной границы. Во-вторых, местоположение подвижной границы устанавливается без перестройки пространственно-временной сетки на каждом новом шаге по времени в отличие от методов МЛФУС и МВФ [9–13]. И, в-третьих, фазовое превращение влаги на подвижной границе рассматривается как процесс с непрерывным отслеживанием агрегатного состава вода-лед от начального до его конечного значения W₀ >  W > 0 [8], где W ₀, W - соответственно начальная и текущая весовая влажность материала в долях единицы. Тогда как в известных методах фазовое превращение влаги на подвижной границе «проглатывается» за один шаг по времени с фиксированием только крайних значений влажности: начальной W = W ₀ и конечной W = 0 [2-4, 9-13].

Для дальнейшей проверки адекватности математической модели в новой постановке наряду с проведенным вычислительным экспериментом [8] мы сравнили результаты численного решения задачи с результатами наблюдений за процессом промерзания влажного материала на физической модели.

В качестве испытуемого материала был использован шлак жидкого шлакоудаления с частицами 2 – 4 мм, полученный при сжигании бурого угля Ирша-Бородинского месторождения со следующими теплофизическими свойствами: W ₀ = 0,065; р th = 1350 кг/м³; Z th = 0,25 Вт/(м\К); C th = 1090 кДж/(м³К); р _f = 1348 кг/м³; Z _f = 0,27 Вт/(мК); C th = 988 кДж/(м³^К).

Физическое моделирование процесса промерзания влажного шлака проведено на экспериментальной установке (рис. 1), воспроизводящей климатические условия г. Красноярска:

• •    продолжительность среднемноголетнего зимнего сезона составляет пять месяцев: с ноября по март включительно;

• •    среднезимняя температура наружного воздуха t out = минус 11 °С;

• •    сезонное промерзание грунтов в г. Красноярске составляет ξ _s∙ f = 2 м.

Геометрический масштаб моделирования в экспериментальной установке принят равным Г = 1/10. При этом толщина слоя шлака в установке с учетом величины сезонного промерзания грунтов составила h _s = Г • ^ _s. f = 20 [2].

Для обеспечения временного подобия процессов теплообмена в модели и реальном шлакоотвале использован критерий тепловой гомохронности Фурье:

_    a • т

Fo = .2 ⁽ h )

11                        .                                                      3 1

где a - коэффициент температуропроводности шлака, м²/с.

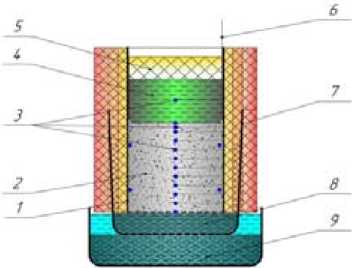
Рис. 1. Экспериментальная установка: 1 - корпус установки с перфорированным дном; 2 - слой шлака; 3 – датчики температуры; 4 – емкость с антифризом; 5 – крышка емкости с антифризом; 6 – кабель датчиков температуры; 7 – внешняя теплоизоляция; 8 – водонасыщенный дренаж; 9 – емкость с крупнообломочным материалом, залитым водой

Согласно этому критерию (2), учитывая, что a' = a , соотношение между временем развития процесса в модели и реальном шлакоотвале составит

т‘

V

2 hsa ^s.f J

т = 0,01 • т

Протяженность зимнего периода в г. Красноярске, как отмечалось выше, составляет пять месяцев, или 3625 ч (725 ч в месяце). Согласно соотношению (3) протяженность «зимнего периода» в эксперименте на физической модели составит 36,25 ч (7,25 ч в месяце).

В качестве корпуса экспериментальной установки использован пластмассовый цилиндрический сосуд диаметром 200 и высотой 300 мм с перфорированным дном (рис. 1). Для устранения влияния бокового теплового потока со стороны стенок внешняя поверхность цилиндрического сосуда была тщательно теплоизолирована.

В сосуд плотно укладывался влажный шлак высотой h'_s = 0,20 м, а под перфорированным днищем сосуда слой дренажа толщиной hd = 0,01 м. В процессе укладки шлака устанавливали десять цифровых термометров DS18В20 с шагом 0,02 м по высоте, а в приповерхностном слое - два термометра с шагом 0,01 м (рис. 1). Контактные выводы термометров витой парой присоединялись к интерфейсной плате персонального компьютера.

Сосуд после засыпки дренажа и шлака был установлен в емкость диаметром 270 мм с гравием на дне, залитым водой до контакта шлак-дренаж. Установка в собранном виде помещалась в холодильную камеру.

Граничное условие I рода на верхней поверхности слоя шлака воспроизводилось путем размещения на этой поверхности тонкостенного алюминиевого цилиндрического сосуда с залитым в него антифризом «IceStream - 45°», охлажденным до минус 12 °С (рис. 1). Когда антифриз в ходе эксперимента нагревался до минус 7–9 °С, его замещали новой порцией охлажденного до минус 12 °С антифриза и т. д. В результате на верхней поверхности шлака воспроизводилось ГУ I рода в виде «пилообразной функции» (рис. 2, кривая 1).

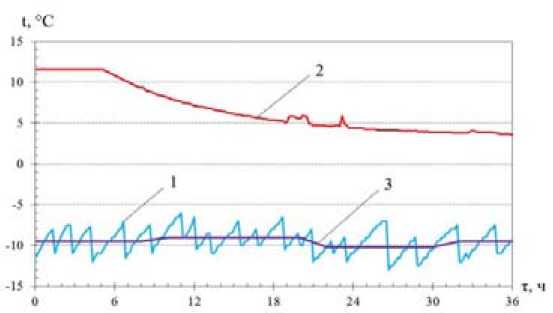
Рис. 2. Температура на внешних поверхностях слоя шлака (ГУ I рода): 1 – температура на верхней поверхности слоя шлака t (0, τ); 2 – температура на донной поверхности слоя t (20, τ) (шлак-дренаж); 3 – средняя по интервалам времени температура наружной поверхности

Математическую модель вышеописанной физической постановки задачи можно представить в виде следующих дифференциальных уравнений:

• •    для внутренних точек мерзлого и талого слоев влажного шлака уравнения теплопроводности вида

. еЧ      8£_   дЧ.

'f = ^л f ,’ ^Cth = ^л th 2 ;

• •    уравнение сопряжения на подвижной границе

  0 =

  
  

  х 7

  I ^д У ² )

  
  

  § * ( т ) + о

  
  

  + [

  I f 5 У²

  
  

  § * ( т )-0

  
  

  ^^^^^^е

  
  

  д W

  q ph ρ

  д т

  
  
  
  

  '

  
  

  ξ^*(τ ),

  
  

  W о >  W >  0 ;

  
  

  ^ (т ) ± dy, W = 0

  
  

  *

  
  
  
  

В уравнении сопряжения (5), представляющем собой уравнение теплопроводности на подвижной границе, отсутствует локальная производная, характеризующая изменение температуры во времени ( ∂ t / ∂ τ). Вода во влажном шлаке находится в свободном, а не в связанном состоянии, как, например, в глинистых грунтах. Поэтому температура фазового превращения воды в лед на подвижной границе - величина постоянная, отсюда ( d t / д т) = 0, и уравнение сопряжения на подвижной границе принимает вид (5).

Для замыкания системы дифференциальных уравнений (4) - (6) были приняты следующие краевые условия:

• •    начальное условие

t (y0) = f (y,0), W(y0j) = Wo, 0 < y < H0 (7)

• •    граничные условия I рода на верхней и донной поверхностях слоя шлака (рис. 2)

t (0 t) = f l (t) ; (8)

t ( h s , t) = f 2 (t) . (9)

Пилообразная функция температуры на верхней (8) и донной (9) поверхностях слоя шлака (рис. 2, кривые 1, 2) в алгоритме задачи были представлены кусочно-линейными функциями вида

f(t) = t0n + kn (Tn+1 - Ti), где t0n - температура на поверхности слоя в начале п-го интервала времени, °С; kn - угловой коэффициент на п-м интервале; тп+1 - конечное значение времени п-го интервала, с; тi - текущее время, с.

Таким образом, процесс теплообмена во всей гетерогенной системе с подвижной границей описывается с помощью уравнений единой физической природы - уравнений теплопроводности вида (4, 5). Единообразие математической модели (4)–(9) позволило применить метод сквозного счета без перестройки пространственно-временной сетки (Δ y = const, Δτ = const) с явным выделением подвижной границы промерзания [8].

В вычислительном эксперименте была использована достаточно подробная пространственно-временная сетка. Шаг по пространственной координате принят равным Δ y = 0,002 м, что для слоя шлака толщиной 0,20 м (рис. 1) соответствовало ста узловым точкам. Величина шага по времени выбрана наименьшей из двух возможных значений для мерзлой и талой зон слоя:

^{А т} = ^{min { A T} 1 ^} , ⁽¹⁰⁾

где Ат < A y ²/2 a i , i = 1, 2 - условие устойчивости для мерзлого i = 1 и талого i = 2 слоев шлака; a i = X i / C i - коэффициент температуропроводности мерзлой или талой зон слоя шлака, м²/с. Таким образом, шаг временной сетки согласно (10) составил Δτ = 6,19 с.

Анализируя результаты математического и физического моделирования (рис. 3), можно отметить, что математическая модель с уравнением сопряжения на подвижной границе достаточно точно, с расхождением 6 – 9 %, описывают общий ход процесса промерзания.

Первоначально в период от 0 до 8,75 ч наблюдалось быстрое промерзание влажного шлака (рис. 3). Это объясняется высокими градиентами температуры, когда на верхней поверхности слоя шлака установилась температура в среднем на уровне минус 9,5 °С (рис. 2, кривая 3) при относительно тонком промерзающем слое шлака.

Затем с 9 до 21 ч температура на поверхности слоя шлака стала несколько выше, чем в первоначальный период, и установилась на уровне минус 9,0 °С (рис. 2, кривая 3) при продолжающемся нарастании ξ(τ). При этом градиенты температуры в промерзающем слое снизились.

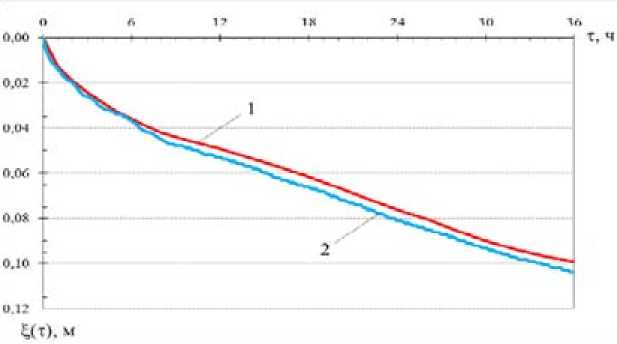
Рис. 3. Вычислительный эксперимент по промерзанию слоя влажного шлака: 1 – кривая промерзания на физической модели; 2 – кривая промерзания в математической модели с уравнением сопряжения на подвижной границе

В результате процесс промерзания замедлился, кривые промерзания 1 и 2 стали более пологими (рис. 3).

На следующей стадии с 21 до 32 ч температура на поверхности шлака понизилась и установилась на уровне минус 10,5 °С. В результате темп промерзания слоя влажного шлака сохранился. Затем с 32 ч до конца эксперимента в 36,25 ч температура на поверхности шлака снова повысилась до минус 9,5 °С (рис. 2, кривая 3), что привело к снижению интенсивности промерзания (рис. 3).

Реализация математической модели с использованием уравнения сопряжения на подвижной границе дает достаточно хорошее совпадение с результатами физического эксперимента. Предложенный метод решения задачи Стефана, прошедший экспериментальную проверку методом физического моделирования и ранее выполненной проверкой известными методами численного решения [8], может быть применен в практических расчетах при изучении процессов теплообмена в гетерогенных системах, сопровождаемых фазовыми превращениями вещества.

• ¹    СНиП 2.02.01-83 " «Основания зданий и сооружений».

• ²    Физические величины, принятые со штрихами, относятся к модели.

• [1]    Основы мерзлотного прогноза при инженерно-геологических исследованиях / под ред. В. А. Кудрявцева. М.: Изд-во МГУ, 1974, 431 с. [ The basics of prognosis of permafrost engineering geological studies. Ed. By V.A.Kudriavtsev. Moscow State University, 1974, 431 p. (in Russian)]

• [2]    Самарский А. А., Моисеенко Б. Д. Журн. вычисл. математики и мат. физики , 1965. 5(5), 816-827 [Samarskii A.A., Moiseenko B.D. Computational Mathematics and Mathematical Physics, 1965. 5(5), 816-827 (in Russian)]

• [3]    Будак Б. М., Соловьева Е. Н., Успенский А. Б. Журн. вычисл. математики и мат. физики , 1965, 5(5), 828-840 [Budak B.M., Solov’eva E.N., Uspenskii A.B. Computational Mathematics and Mathematical Physics , 1965, 5(5), 828-840 (in Russian)]

• [4]    Самарский А. А., Вабищевич П. Н. Вычислительная теплопередача . М.: Едиториал УРСС, 2003. 784 с. [Samarskii A.A., Vabishchevuch P.N. Computational heat transfer , Moscow, Editorial URSS, 2003. 784 p. (in Russian)]

• [5]    Хаглеев, Е. П., Хаглеев Ф. П. Гидродинамика больших скоростей : межвуз. сб. КрПИ. Красноярск, 1992, 63-69 [Khagleev E.P., Khagleev P.F . Hydrodynamics of high speeds , Krasnoyarsk, 1992, 63-69 (in Russian)]

• [6]    Хаглеев Е. П., Хаглеев П. Е. Труды II Российской национальной конференции по теплообмену . Т. 6. Интенсификация теплообмена. Радиационный и сложный теплообмен. М.: Изд-во МЭИ, 1998, 216–219 [Khagleev E.P., Khagleev P.F. Proceedings of II Russian national conference on heat transfer, Vol. 6, Moscow, National Research University “MPEI”, 1998, 216-219 (in Russian)]

• [7]    Khagleev E. P. J. Sib. Fed. Univ. Eng. technol., 2013, 5(6), 485–497.

• [8]    Khagleev E. P. J. Sib. Fed. Univ. Eng. technol., 2014, 7 (8), 894–910.

• [9]    Будак Б. М., Гольдман Н. Л., Успенский А. Б. Решения задач типа Стефана . М.: Изд-во МГУ, 1972, вып. 2, 3-23 [Budak B.M., Goldman N.L., Uspenskii A.B. Solving Stefan-type problems, Moscow State University, 1972, vol. 2, 3-23 (in Russian)]

• [10]    Crank J. Free and Moving Boundary Problems . Oxford, Clarendon Press, 1984, 425 p.

• [11]    Douglas J, Gallie G. M. On the numerical integration of a parabolic differential equation subject to a moving boundary condition. Duke Math. J., 1955, 22(4), 557-572.

• [12]    Javierre-Perez E. Literature Study: Numerical methods for solving Stefan problems Delft University of Technology, Report 03-16, 2003, 94 p.

• [13]    Красношлык Н. А., Богатырев А. О. Вiсник Черкаського унiверситету. Серiя При-кладна математика. Iнформатика , 2011, 194, 11–31 [Krasnoshlyk N.A., Bogatyrev A.O. Herald of Cherkasy University. Applied mathematics, computer science , 2011, 194, 11–31 (in Ukrainian)]