Верификация математической модели виброакустического датчика

ческое исследование поведения датчика в исследуемой жидкой среде и, следовательно, необходимо совместное решение уравнений теории упругости и гидромеханики. Это требует разработки специальных математических моделей, так как решение подобных задач в известных вычислительных системах зачастую содержит непреодолимые трудности, связанные, например, с изменением области определения задачи гидромеханики до 90– 99 % за период колебаний, что приводит к потере сходимости численной схемы.

Математическая модель виброакустического датчика

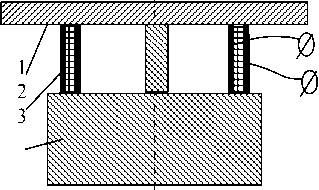
Простейшая модель датчика состоит из пластины 1, пьезоактивного элемента 2 и концевой массы 3, как показано на рис. 1.2

Разобьем упругодеформированную систему на рис. 1 на элементарные подсистемы: пластина – стержень – цилиндр – инерционная масса и запишем уравнения движения каждой из них. Уравне-

а)

б)

Рис. 1. Модель виброакустического датчика: а) клеевая, б) сборная ние малых поперечных колебаний [2] круглой изотропной пластины 1 запишем в виде:

D A r ^ A _{r 0} w + р h ( d ² w I' d t ²) = Ф ( r , 0 , t ),           (1)

где A _{r e} = [( d ²I d r ²) + (1I r )( d I d r ) + (1I r ²)( d ²I d0 ²)] -оператор Лапласа; Ф ( r , 0 , t ) - функция возмущений; D = Eh ³I[12(1- ct ²)] - цилиндрическая жесткость; р - плотность материала; E - модуль Юнга; ст - коэффициент Пуассона; h - толщина; r - радиус; 0 - окружная координата.

В качестве краевых условий используются условия свободного края, которые определяют равенство нулю изгибающих моментов и перерезывающих сил на граничном контуре пластины:

M_r = - D {( d ² w I d r ²) + ст [(11 r )( d w I d r ) +

+ (1I r ²)( d ² w I de ²)]} = 0, при r = R 1 ,            (2)

Q_r = - D {( d i d r )( A _{r 0} w ) - (1I r ) ( d I d0 ) X

X [(1- CT )( d i d r ) (1I r )( d w I d0 )]} = 0, при r = R 1 . (3) Начальные условия имеют вид:

w ( r , 0 , t = 0) = w i ( r , 0 ); d w ( r , 0 , t = 0)I d t = w ₂( r , 0 ).

Функция Ф ( r , 0 , t ) включает возмущения, наложенные на пластину со стороны внешней среды, в том числе через краевые и начальные условия. В соответствии с работой [3] имеем:

Ф ( r , 0 , t ) = P ( r , 0 , t ) - G 1 S ( r - r 0 ) - F 1 8' ( r ) +

+ p h [ w 1 ( r , 0 ) 8 ( t ) + w 2( r , 0 ) 8' ( t )].              (4)

В этом выражении P ( r , 0 , t ) - распределенная по площади нагрузка со стороны жидкости, заключенной или в тонком прилегающем слое, или в неограниченном пространстве; G 1 - интенсивность реакции связи со стороны цилиндрического пьезоэлемента, равномерно распределенная по окружности радиуса r 0 ; F 1 - сосредоточенная реакция связи со стороны пьезоактивного стержня; R ₁ -внешний радиус пластины; 8 , 8 _r ', 8 _t ' - дельтафункция и ее производная по координате r и времени t .

Уравнение продольных колебаний пьезоэлемента 2 в виде цилиндра или стержня приближен- но описывается волновым уравнением (модель тонкого стержня):

d ² u i I d t ² = c i ² k f ² d ² u i I d x ²,                           (5)

где i = 1 относится к стержню, i = 2 - к цилиндру; C j ²= E Ui I p i - скорость распространения звука в пьезоактивном материале; р i - плотность, k f - коэффициент поправки на конечное значение толщины столбика и цилиндра.

Условия на краях пьезоэлемента 2:

E U 1 A r ₀ d u 1 I d x = G 1 + G ₀ ( x = 0),

EU1A rndu 1Idx = - G 2-G 0 (x = l),(6)

E U ₂ S d u ₂I d x = F 1 + F ₀ ( x = 0),

EU2Sdu2Idx = -F2-F0 (x = l).(7)

Уравнение движения концевой массы 3 имеет вид:

d2 vIdt2 = 2л r0 G 2 + F2.(8)

Уравнения пьезоэффекта запишем в форме с константой Г [4]:

d u 2 I d x = ( G 0 + Г 12 P )I S P ,

P = e( U + Г 12d u 2Idx),(9)

где s^P = s^U + е Г₁₂ - упругость пьзоэлемента 2 при постоянной поляризации P ; s^U - упругость пьзо-элемента при постоянном электрическом поле ( U - напряженность поля); E^U i - модуль упругости первого рода при постоянном электрическом поле; F ₀ и G ₀ - эквивалентные пьезоактивные сила и интенсивность силы, приложенные к концам стержня и цилиндра и определяемые через уравнения пьезоэффекта (9).

Условия сопряжения по перемещениям:

u 1 (0) = w (0), u 2 (0) = w ( r 0 ), u 1 (l) = u 2 (l) = v .

Часто в измерительной практике приходится создавать излучатели или приемники со сферической излучающей (принимающей) поверхностью, что обеспечивает высокую пространственную избирательность измерительного сигнала и получение более детальной информации. Математическая модель такого датчика аналогична вышеизложенной модели (1)-(9), однако уравнение поперечных колебаний пластины надо заменить на уравнения колебаний пологой сферической оболочки, которые в обозначениях работы [2] имеют следующий вид:

D A _{r 0}A _{r 0} w + R ^-1 A , еф + p h ( d ² w I d t ²) = Ф ( r , 0 , t ), (10) A 11 A r eA ^ф - R 1 A ^ 0 w = 0,                        (11)

где R - радиус сферы и ф - угловая координата сферической оболочки. Очевидно, что при радиусе R ^ ^ уравнения (10) и (11) переходят в уравнение (1). Метод решения основан на использовании функций Грина пластины и сферической оболочки, а собственно модель датчика формируется на основе структурной теории распределенных систем [3], аналогично работе [1].

Используемые модели содержат ряд ограничений, связанных с приближениями теории пластин и оболочек, неточностью описания колебаний стержня и пьезоцилиндра 2 волновым уравнением, отсутствием учета влияния смежных форм колебаний другого типа, которые приводят к появлению комбинационных частот, и т. д. Возникает также вопрос о методической погрешности вычисления собственных частот и форм колебаний, который можно снять верификацией разработанной модели на основе численного и натурного эксперимента. В качестве численного верификатора выбрана вычислительная среда SolidWorks со встроенным конечно-элементным приложением CosmosWorks, имеющая сертификат качества американского и европейского образца. Предлагаемая модель датчика реализована c использованием вычислительных возможностей пакета Matlab.

На рис. 2 представлена амплитудночастотная характеристика датчика, полученная на основе расчетных амплитуд колебаний на краю пластины по разработанной нами модели. Зависимости получены при следующих параметрах датчика: радиус пластины – 30 мм; толщина – 3 мм; модуль упругости пластины и стержня – 2,1·1011 Н/м2, модуль упругости пьезокерамического материала цилиндра – 2,21·1011 Н/м2, длина стержня – 30 мм, длина пьезоэлемента – 15 мм, масса концевого элемента – 300 г, плот- ность материала пластины и стержня – 7,8·103кг/м3, плотность пьезокерамики – 2,3·103кг/м3, коэффициент Пуассона материалов – 0,29. На рис. 2 можно увидеть, что значение второй резонансной частоты составляет f02 = 7460 Гц. Сравнивая рис. 2 и 3, видим, что амплитуда колебаний датчика в окрестности третьей резонансной частоты примерно в 2,5 раза меньше, чем в окрестности второй. Этот же факт отражен и на рис. 5, где диаметр диаграммы кругового кинетического импеданса [4] для 3 резонансной частоты существенно больше диаметра в окрестности второй частоты. Фазочастотная характеристика представлена на рис. 4 и необходима для построения диаграмм кинетического импеданса. Диаграмма кругового кинетического импеданса в околорезонансной области показана на рис. 5, вторая и третья формы колебаний представлены на рис. 6.

Частотные характеристики и околорезонанс-ные диаграммы кинетического импеданса содержат в себе необходимые идентификационные признаки, на основе которых решается задача определения состава жидких сред. Например, анализируя

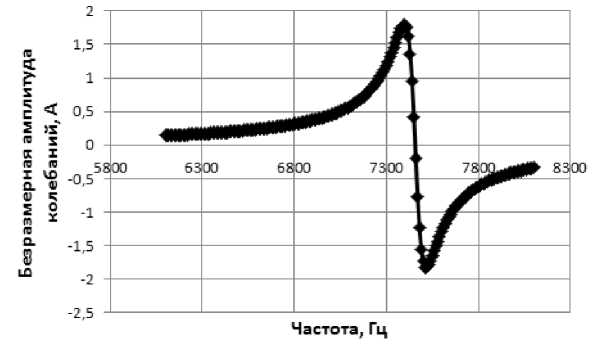
Рис. 2. Частотная характеристика амплитуды колебаний на краю пластины в окрестности второй резонансной частоты ( f 02 = 7460 Гц)

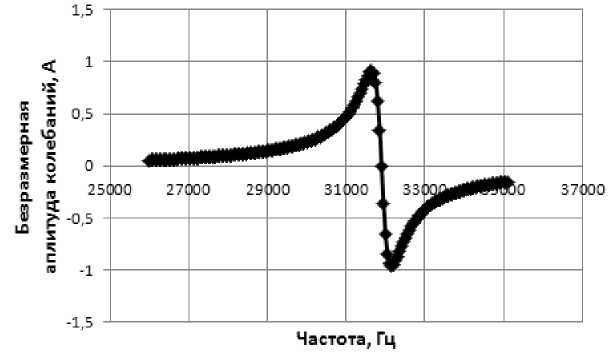
Рис. 3. Частотная характеристика амплитуды колебаний на краю пластины в окрестности третьей резонансной частоты ( f 03 = 31900 Гц)

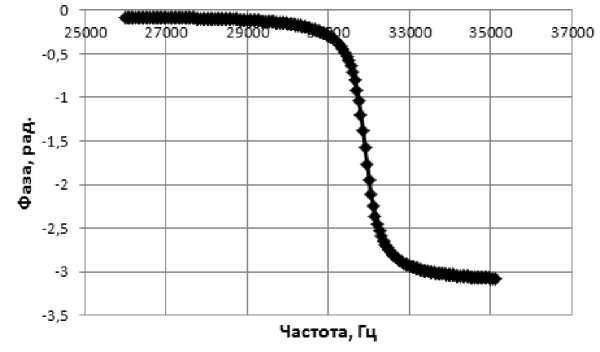
Рис. 4. Фазочастотная характеристика в окрестности третьей резонансной частоты колебаний f 03

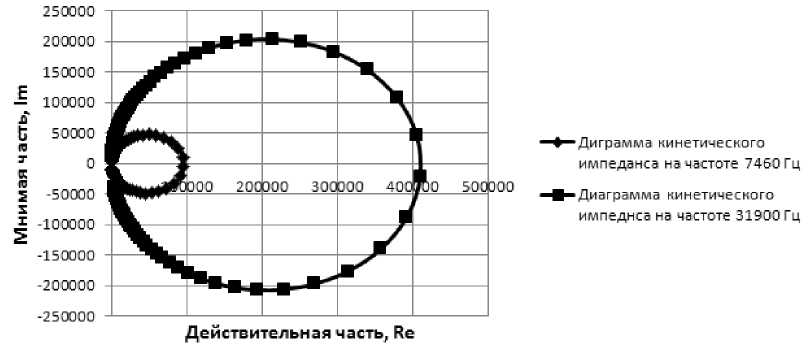
Рис. 5. Диаграммы кругового кинетического импеданса в окрестности частот f 02 = 7,46 кГц и f 03 = 31,9 кГц

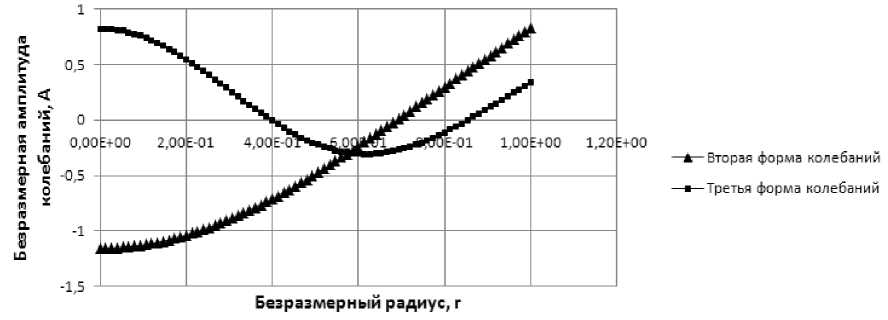
Рис. 6. Вторая и третья формы колебаний

диаграмму кинетического импеданса, можно выделить следующие параметры: резонансная частота; квадрантные частоты; диаметр круговой диаграммы кинетического импеданса. Здесь резонансная частота связана с параметрами пластины и жидкости по формуле f0 " 21Г ' (12)

где r - радиус пластины; E - модуль Юнга; р - плотность пластины, которые функционально связаны с параметрами элементов датчика и присоединенной массы жидкой среды, и установление этой связи является одной из решаемых задач.

а)

Рис. 7. Натурная (a) и численная (б) модель виброакустичсекого датчика, полученная в среде Cosmos Works

б)

Альтернативные статистические методы не дают требуемой точности идентификации жидких сред и, особенно, при сложном, динамически изменяемом составе.

Сравнение результатов расчета на основе сопоставления величин собственных частот и форм колебаний, полученных с помощью разработанной и конечно-элементной модели CosmosWorks, дает погрешность вычислений на уровне 5,3 %. Данная погрешность является следствием описанных выше допущений теоретической модели. Был изготовлен также натурный макет датчика (рис. 7, а). Исследование этого макета было проведено с использованием фигур Хладни, которые на частоте резонанса позволяют увидеть реальную форму колебаний с помощью сыпучей среды, нанесенной на поверхность пластины. Форма колебаний соответствует теоретической, при этом третья резонансная частота составила 30,366 кГц, что также достаточно близко лежит к расчетной частоте и совпадает с частотой численного верификатора 30,190 кГц с относительной погрешностью 0,6 %.

Заключение

Разработана распределенная модель виброа-кустического датчика, которая показала хорошее совпадение с данными натурного и численного эксперимента. Дальнейшая работа должна привести к появлению методики и программного обеспечения для идентификации жидких сред на основе околорезонансных измерений, а также устройств для измерения парциальных значений плотности, вязкости и расхода.