Вероятность нарушения связи в сотовой сети мобильной радиосвязи в условиях замираний сигнала и помехи

Вероятность нарушения связи является основным эксплуатационным показателем качества обслуживания в сотовых системах подвижной радиосвязи. Для выполнения инженерных расчетов при проектировании сотовых систем часто используются модели распространения радиоволн, основанные на эмпирических зависимостях Хаты и Окамуры. Однако для теоретического анализа вероятности нарушения связи целесообразно использовать строгую и достаточно общую модель замираний сигналов в канале радиосвязи, основанную на четырехпараметрическом распределении комплексного коэффициента передачи каждого учитываемого сигнала. Проявляющиеся на практике виды замираний (райсовские, рэлеевские и более глубокие замирания) характеризуются определенным и фиксированным набором параметров используемого четырехпараметрического распределения. В статье представлена методика анализа, основанная на четырехпараметрическом описании замираний сигнала и помехи. Получены точные формулы для вероятности нарушения связи.

Постановка задачи

Рассмотрим сотовую сеть мобильной радиосвязи, в которой передаваемый сигнал испытывает многолучевое распространение в замирающем канале. В месте приема наряду с полезным сигналом присутствуют L сигналов соканальной помехи от БС, в которые используют одинаковые частотные группы:

L

z (t) = Yoei80 so (t)+ Ё Ykei9k sk (t),        (1)

k= 1

где s ₀ ( t ) - полезный сигнал,а { s k ( t ) , k = 1, L } - со-канальные помехи, γ _k и θ _k – амплитуда и фаза комплексного коэффициента передачи у _k k -го канала.

Ограничимся рассмотрением только амплитудных характеристик каналов, считая, что:

• -    случайные величины Y k , k = 0, L статистически независимы;

• -    з акон распределения случайных величин γ _k , k = 0, L , четырехпараметрический [1] с функциями

плотности вероятности f_k ( у ) , математическими _ 2    _2

ожиданиями m x _k , my _k и дисперсиями о x , _k , о y , _k квадратурных компонент X _k и Y _k вел ич ин γ _k .

Пусть ^ о = |Y o|² и ^ k = |Y k|2 , ^k = 1L — мгновенные значения мощности полезного сигнала и соканальных помех в месте приема, тогда для удовлетворительногоприема необходимо[2],что-бы мощность ξ 0 гарантированно (скажем, _L в r -раз) превосходила суммарную мощность ^ = E ^ k .С k=1 этой точки зрения выражение для вероятности нарушения связи имеет вид:

P out = Pr { r^ >  ^ 0 } .               (2)

V1 - 2i< k t

Теперь задача сводится к статистическому исследованию случайной величины а = r ^ - ^ 0 и определению вероятности ситуаций, когда

≥0 ⇒ прекращение связи;

<0 ⇒ удовлетворительный прием.

Вероятность нарушения связи

Задачу отыскания вероятности нарушения связи можно считать решенной, если будет найден закон распределения случайной величины α . Для этого воспользуемся аппаратом характеристических функций. По определению того       L L         \

V a ( t ) = J •••/exP i I r E ^ k — ^ 0 I t

0   0 L V k = 1            7

X f ( ^ 0 ^ ,...,^ L ) d ^ 0 d^ ... d ^ L

X

где f ( ^ 0 Л1 ,...,^ _L ) - функция распределения вероятностей случайных величин ^ ₀Л1 ’.-ЛL . Пусть v _k ( t ) — характеристическая функция ^ _k , к = 0, L , тогда, учитывая свойство характеристической функции суммы независимых случайных величин [3], получим:

L

V a ^{( t} ) = V ^ o ⁽ "t ) П ^k ⁽ rt ) ■         ⁽5)

k= 1

В условии справедливости четырехпараметрической модели квадратурные компо нен ты X _k и Y k коэффициента передачи Y k , k = 0, L , считаются нормальными случайными величинами. При этом характеристические функции величин X _k и Y _k имеют вид:

V X k ( t ) = exp ( ^im x,k t - <_kt ² /2 ) , Wk ( t ) = exp ( ^im y,k t - ° y,k t ² 12 ) .

Учитывая, что

^ k = |Y k I² = X 2 + Y k ² ,              (7)

характеристическая функция величины ξ _k (аналогично (5)) запишется как

V^ ⁽ t ) = V X 2 ^{( t} ) V ^ ⁽ t ) ,            (8)

где v X 2 ( t ) , V_Y 2 ( t ) — характеристические функции величин X _k ² , Y _k ² ,

V X ^{2 ( t} ) =

exp [ im ² k V ( 1 — 2 i ^ Xj, t ) ]

V Y _k 2 ^{( t} ) =

exp [ im y , k у ( 1 - 2 i ^ y , k t ) ] V1 - 2i^ y t

Далее определим функцию распределения

F ( a ) величины a по известной характеристической функции v _a ( t ) . Согласно [4]

F ( x ) = 1 - ¹ J im [ _V ( t ) e- itx ] dt ,     (10)

2π0         t где F (x) и V (t) — функция распределения и характеристическая функция величины x; Im [z] -функция мнимой части от z.

С учетом (3) и (10) формула (2) примет вид:

P out = Pr { a >  0 } = 1 - Pr { a <  0 } =

= 1 — F ⁽ 0 ) = 2 ₊ П J Im [ ^ a ( t ) ]^tt ■    ^(П)

Подставляя (5) в (11) с учетом (8) и (9), итоговое выражение для вероятности нарушения связи, когда в месте приема присутствуют полезный сигнал и L -сигналов интерференции, замирающих по закону (2), примет вид (12) – см. с. 29.

Анализ формулы (12)

Исследуем влияние замирающих параметров на вероятность нарушения связи. Ограничимся случаем семиэлементной структуры размещения сот с шестью источниками помех по основному каналу приема ( L = 6). Кроме того, вместо m _x , m _y , σ ² _x , σ ² _y введем иные параметры, имеющие более наглядный физический смысл [1]

Y = a _r + a, + m, + m„ xy x y

– средний коэффициент передачи канала по мощности (средний квадрат модуля коэффициента передачи канала).

exp

Pout=1+1

2π0

×sin

L

I

k = 1

² ( m x,0 ° x,0 t ) ²

1 + (2c2 ot) x,0

² ( m y,0 ° y ,0 t ) ²

1 + (2° t)2

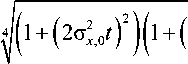
2=V«t ) 2 ) П [ ( 1 + ( ' k = 1 L\

⎛ 2

^⎛⎜       rm x , k ^t

^⎜1+ 2 r σ ² t ⎝ x , k

2 rm y , k ^t

1+ 2 r σ ² t y , k

m x ,0 ^t            m y ,0 ^t

2 ^- 2

1 + (2°2 ot)    1 + (2°2 ot)

x ,0                     y ,0

-

L

I

k = 1

² ( rm x,k ° x,k t )      ² ( rm y,k ° y , k t )

2 +                 \2

2 r σ ² t 1+2 r σ ² t ^⎟ x , ky , k ⎠

×

) 2                       2

1 + (2r° kt)

y ,

-

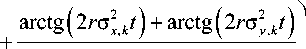
arctg (2°2,ot)+ arctg (2° yot)

dt

. t

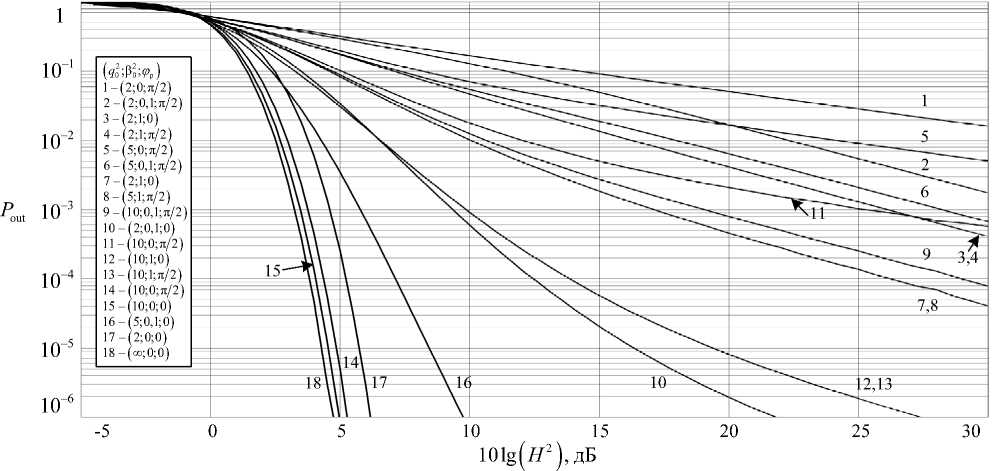
Рис. 1. Зависимость вероятности нарушения связи при различных параметрах q 0 , в 0 , ^ _р0

22   2

2   m x ⁺ m y    Y р     2_

q =——г=——-, q ^0

^ x ⁺ ^ у    ^ х ⁺ С у

– отношение средних мощностей регулярной и флуктуирующей частей сигнала;

в2 = а2/ay , 0 < в2 < 1           (15)

– отношение, характеризующее степень асимметрии канала по ортогональным компонентам;

^ р = arctg ( m y /m x ) , ⁰ ^ ^ p ^ ^П/^{2 (16)} – фазовый угол вектора γ _р (регулярной части сигнала) в системе координат XY .

Для L = 6 параметры распределений сигналов интерференции имеют вид:

⎛ ⎜ γ 12 ⎜⎜ γ 22 ⎜⎜ γ 32	q 12 q 22 q 32	β 12 ϕ р,1 ⎞ β 2 ϕ р,2 β 3 ϕ р,3		⎛5,5 4,2 0,56 π 4 3,2 2,0 0,30 π 2
				⎜5,1	4,1 0,59 π 4
⎜⎜ γ 24	q 42	β 4 ϕ р,4		⎜3,8	2,2 0,28 π 2
⎜ 2	2	2		⎜⎜4,9	3,9 0,50 π 4
⎜γ 5	q 5	β 5 ϕ р,5		⎜⎝3,6	2,5 0,35 π 2
⎜⎝γ 26	2 q 6	β 6 ϕ р,6 ⎠

.

Поскольку ная структура

рассматриваемая семиэлемент-размещения сот уже обеспечи- вает разницу в мощности сигнала и помех по основному каналу приема в 15 дБ [2], примем, что коэффициент r = 1. Зависимость вероятности нарушения связи Pout (H2) от значения

H 2 при различных параметрах q 0 , в 0 , ^ _р , _о полезного сигнала представлена на рис. 1. Под величиной H ² будем понимать отношение средней мощности сигнала в месте приема к суммарной средней мощности сигналов интерференции

часто используется двухпараметрическое m -распределение Накагами

f ⁽ Y ) =

m′ 2m′-1

2m Y     -™у/ у2

e m′

Г (m') Y

H ²

^γ 0 ²

L

Z Yk

k =1

•

где m >  1(2 - параметр, выражающий отношение квадрата средней мощности принимаемого сигнала к дисперсии его мгновенной мощности

Из кривых на рис. 1 видно, что при достаточно большом значении параметра q ₀ ² ≥ 10 можно обеспечить вероятность нарушения связи, не превышающую 10^-2, при значении H ² <  25 . Коэффициент асимметрии β ² ₀ в меньшей степени влияет на вероятность нарушения связи, чем параметр ^ _р , ₀ .

Уменьшение q 0 ведет к повышению вероятности нарушения связи, однако при наличии сильной асимметрии по ортогональным компонентам ( β ₀ ² → 0 ) все же возможно обеспечить прием и в каналах, где q 0 >  2 .

Когда q 2 близко к нулю (подрэлеевский канал [1]) удовлетворительное значение вероятности нарушения связи можно обеспечить значением H ² >  30 .

Обобщение результатов

Для описания распределения амплитуд γ наряду с четырехпараметрическим распределением

m

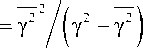
В [4] для случая, когда в месте приема наряду с полезным сигналом присутствует L сигналов интерференции, выражение для P _out имеет вид:

Pout=1+1∞⎡⎢1+

2π0 ⎢⎣

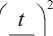
⎝λ0 ⎠

^m 0 ^′

2L

п

k=1

1+

2 ⎛rt⎞

λ

k

^m k ^′

×

× sin

L

Z mk arctg k=1

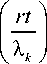
m ₀ ′ arctg

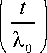
dt

, t

где X k = m k/Yk , k = 0,L •

Известно [1], что распределение (18) удовлетворительно аппроксимирует четырехпараметрическое распределение в опреде ле нной области изменения четырех параметров Y 2 , q 2 , в 2 , Ф р , поэтому представляется интересным сравнение соответствующих вероятностей (12) и (20).

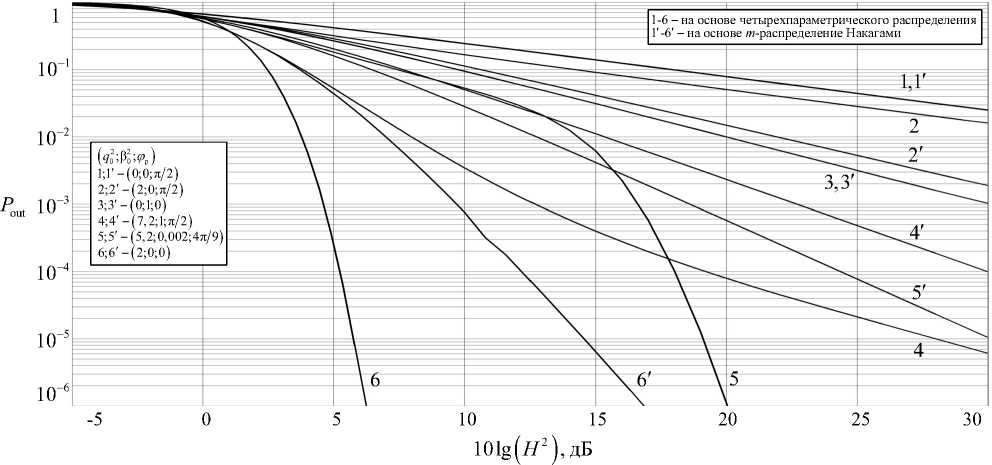
Рис. 2. Зависимость вероятности нарушения связи при четырехпараметрическом распределении и m -распределении Накагами для различных параметров q 0 , в о , ф р о

Исходя из определения (19), найдем m′ для канала с четырехпараметрическим распределением амплитуд о, + о„ + mx + mv) xy x y

44  22  22

2(ог + о,, + 2огmr + 2о,,m„ ) xy  xx  yy

__________________(1 + q2 +e" )2__________________ 2[1 + e4 + 2q2 (1 + e2 )(e2 cos2 фр + sin2 фр )]

Зависимость P out ( H ² ) при четырехпараметрическом распределении и m -распределении На-кагами для различных параметров q 2 , в 0 и ^ _р,о полезного сигнала представлена на рис. 2.

Как видно из рис. 2, степень расхождения кривых, построенных по формулам (12) и (20), колеблется в значительных пределах. Совпадение кривых наблюдается в случаях рэлеевского и усе-ченно-нормальногоканалов(кривые 1 , 1′ и 3 , 3′ соответственно). При неравных дисперсиях орто- гональных компонент расхождение значительно усиливается. В силу того, что двухпараметрическое m-распределении не в состоянии воспроизвести всю тонкую структуру четырехпараметрического распределения, результат (12) следует рассматривать как обобщение результата (20).

Выводы

В статье решена задача определения вероятности нарушения связи в условиях справедливости четырехпараметрического распределения амплитуд сигналов мобильной радиосвязи. Данная модель является общей моделью радиоканала, позволяющая исследовать практически любые виды замираний сигнала, встречающихся в реальных условиях. Поэтому результаты статьи обобщают результаты, ранее полученные в [4, 5]. Следует отметить также,что при использовании четырехпараметрического распределения появляется возможность учитывать фазовые замирания. Это обстоятельство оказывается весьма полезным, если при расчете вероятности нарушения связи использовать характеристики алгоритма обработки принимаемого сигнала, в том числе и оптимального, использующего интерференцию полезного сигнала.