Вероятностная модель процесса продольной ориентации стеблей соломы зерновых культур
Автор: Ермольев Юрий Иванович, Бутовченко Андрей Владимирович, Белов Сергей Владимирович, Фоменко Роман Евгеньевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 6 (67) т.12, 2012 года.
Бесплатный доступ
Приведён общий подход построения стохастической математической модели процесса продольной ориентации длинных соломистых фракций на специальном ориентирующем устройстве.
Стохастическая модель, сепаратор-ориентатор, соломистые фракции, показатели процесса
Короткий адрес: https://sciup.org/14249901
IDR: 14249901 | УДК: 631.362.001.573
Текст научной статьи Вероятностная модель процесса продольной ориентации стеблей соломы зерновых культур
Введение. Структурный синтез рациональных совокупностей частных технологических операций, способных выполнять ориентацию стеблей зерновых культур для последовательного их изменения с заданными параметрами, предопределяет необходимость оценки основных технологических показателей функционирования ориентирующего устройства стеблей зерновых культур (ОУСЗК). В связи с этим возникла необходимость параметрического и структурного синтеза ОУСЗК при ориентации стеблей зерновых культур с различными размерами стеблей.
Построение модели. Рассмотрим в общем виде стохастическую модель процесса продольной ориентации стеблей на ОУСЗК. Принципиальная схема устройства для ориентации стеблей зерновых культур представлена на рис. 1.
Соломистый Ьорох
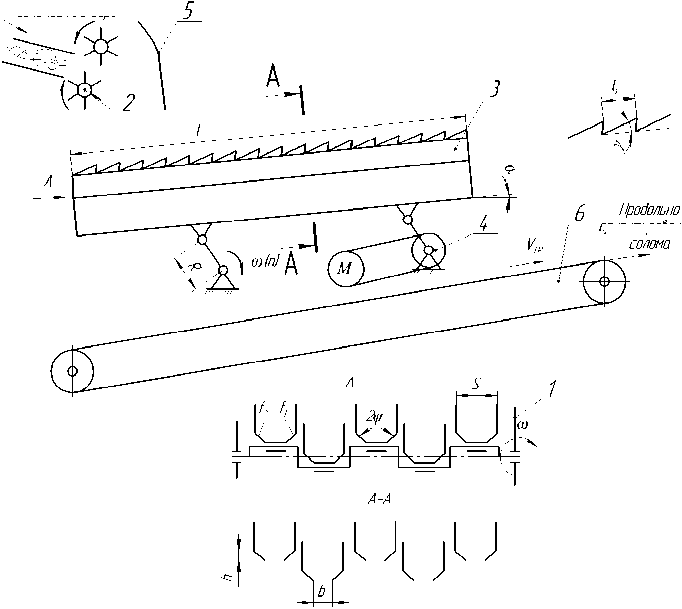
Рис. 1. Принципиальная схема устройства для ориентации стеблей зерновых культур: 1 — боковины устройства; 2 — устройство для разрушения тюков соломистого вороха; 3 — клавишный сепаратор-ориентатор; 4 — привод клавиш сепа-раторов-ориентаторов; 5 — направляющий щиток; 6 — транспортёр ориентированной соломы
ороЕншорсЛанная
Основными геометрическими параметрами ОУСЗК являются его длина / и ширина В, угол о наклона его к горизонту, частота п оборотов кривошипа радиуса R ; шаг S установки гребёнок, их конструкция (/Г/ у), высота h и угол 2qj установки стенок желобков, ширина b выходных щелей между гранями гофров; скорость VTP ленты транспортёра.
ОУСЗК можно представить в виде двух расположенных друг над другом и неоднородных «условных» решёт равной длины /, каждое из которых обладает отличным от другого, но постоянным для отдельного решета коэффициентом сепарации цу.
Верхнее условное решето представляет собой слой соломистого вороха на сепараторе и линейчатую поверхность сепаратора с шагом S, нижнее условное решето образовано желобками гофров с выходными щелями шириной Ь. Для первого верхнего решета для второго решета
М2, = где Q — подача стеблей зерновых культур (СЗК) на ОУСЗК; И/ — влажность СГС; /(/у), ^Ьш]) — плотности вероятностей распределения длины /у и ширины b j-x компонентов СЗК; yt и у2 — вероятностная доля а, — компонентов, способных пройти в щель ОУСЗК 5 и Д; fbj — коэффициент внутреннего трения>го компонента; р — плотность массы СЗК; пи R — частота и радиус кривошипа, обеспечивающие подброс компонентов СЗК относительно рабочей поверхности ОУСЗК; VTP — относительная скорость перемещения компонентов СЗК по сепара-тору-ориентатору ОУСЗК. Ограничением прохода j-x компонентов СЗК через условное первое и второе решёта ОУСЗК являются соответствующие условия
ьш] < Ь;
1^ и ^гз — средние скорости относительного перемещения >х компонентов по условному первому (рабочая поверхность ОУСЗК) и второму (желобки между стенками гофров) решётам.
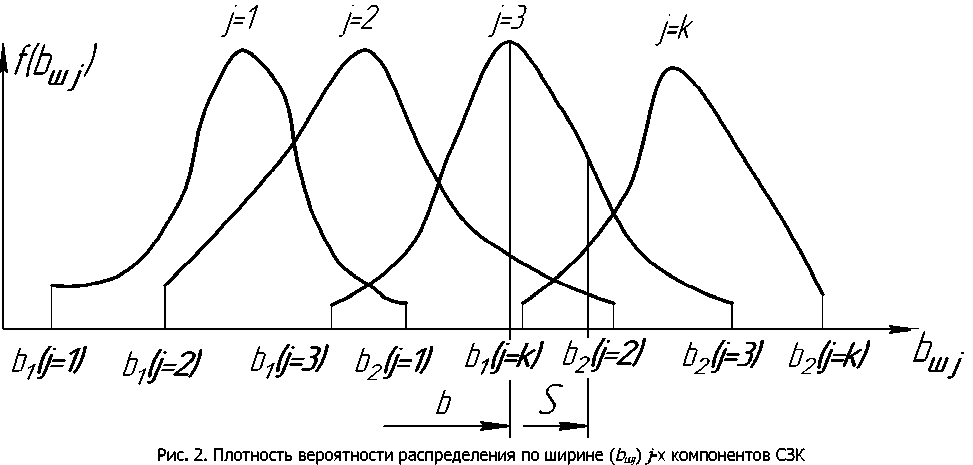
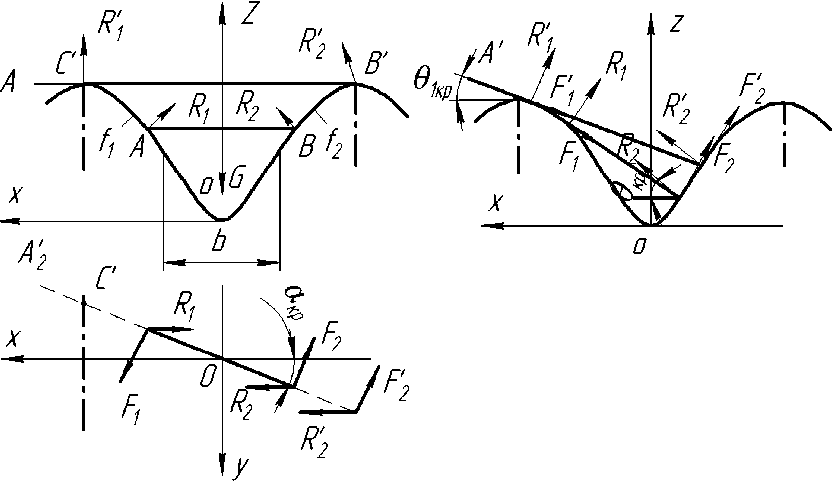
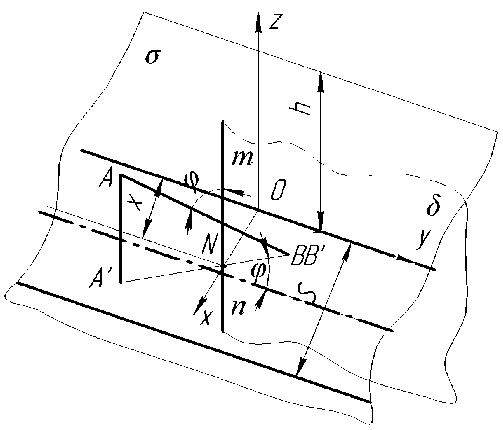
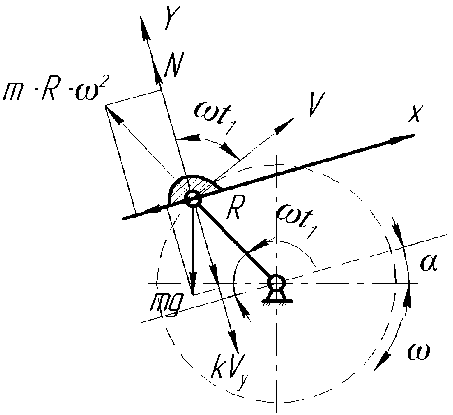
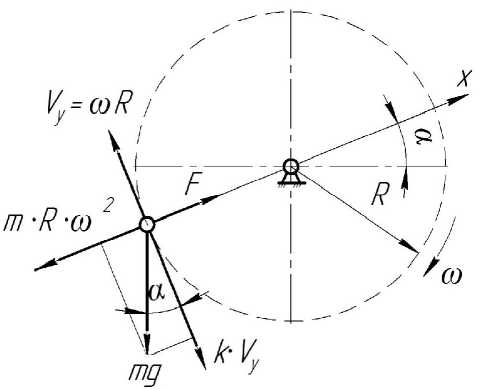
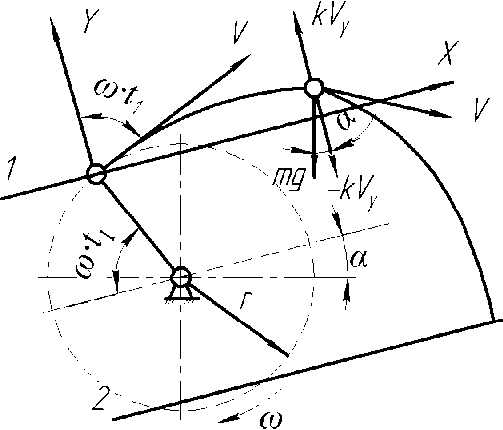
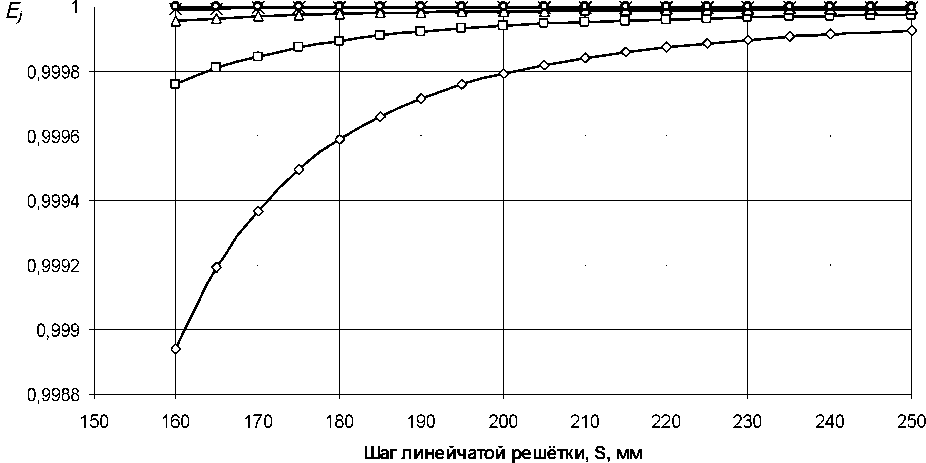
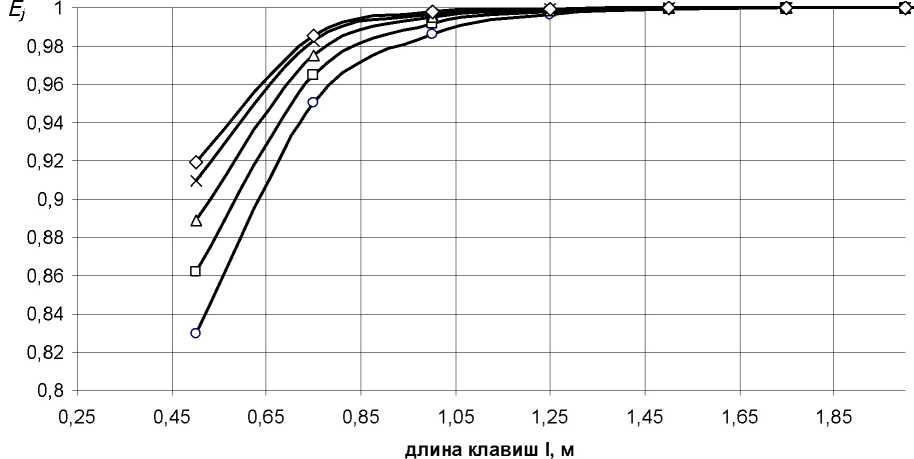
При условии содержания к компонентов (j- 1, 2, ..., А) в исходных СЗК с известными плотностями вероятности f^b^ распределения по ширине (рис. 2) и задаваемой шириной 8 и b (см. рис. 2) размеров щелей условных первого и второго решёт вероятностная доля Y1 j-x компонентов, способных пройти щель шириной 8, например, для условия j = 3, 8 Y1(7=3) й2у=3) ' [ f (b Adb ^и-з) при b^S^N^l. Тогда часть j-x компонентов СЗК, идущих в сход с 1-го условного решета Qlcxj Q1C4=Q. a7(l-Y1).(5) По аналогии, например, для условия = f f(b Adb / V Mb Adb ,(6) Ь2и=21 / ^(7 = 2) тогда часть j-x компонентов СЗК, прошедших щель шириной 8 первого условного решета, сойдёт в сход Q2jc со 2-го условного решета Q„ = Q,'h (i-v2).(7) Для этих условий полнота просеивания Eiy>ro компонента СЗК на ОУСЗК длиной /будет [1] £у =1 - (м27 • ехр (-р17/) - р17/ • ехр (-р27/))/(р27 - р17),(8) а просеивание с продольной ориентацией >го компонента в единицу времени на ОУСЗК длиной / определяется из выражения Г„7 =Q-a7-Y1.Y2.e7,(9) Для аналитического описания коэффициентов сепарации р17 и р2у введём допущения [2]: 1) >е компоненты распределены равномерно в слое СЗК; 2) >е компоненты СЗК, способные «пройти» первую и вторую щель (5 и Ь) условных решёт, имеют прямолинейную цилиндрическую форму тела длиной tj, равной длине этого компонента, и шириной Ь^; 3) плотности вероятностных случайных величин lj и /ш; подчиняются нормальному закону; 4) центр масс j-x компонентов совпадает с их геометрическим центром; 5) проход >го компонента через соответствующие щели условных решёт определяется нахождением его центра масс в плоскости щели и положением в пространстве, обеспечивающим проход в отверстие без касания его кромок половиной длины tjj-vo компонента. Тогда [2]: (ю) где Ру — вероятность прохода >го компонента вороха соответственно через слой СЗК на рабочей поверхности сепаратора ОУСЗК и через его условное линейчатое решето с шагом 5; 1щ — среднее время одного цикла перемещения >го компонента на первом условном решете; Иу — средняя относительная скорость перемещения >го компонента на первом условном решете. Вероятность ^представим в виде комбинации двух несовместных событий ^=^17(1-^) Для 5>ЬЩ, (И) где P2j — вероятность непрохода >го компонента соломистого вороха через линейчатое решето с шагом линий S (вероятность пересечения компонентом при опускании на сепаратор двух и более линий) за один цикл его перемещения по линейчатому решету; РС1 — вероятность прохода >го компонента через слой соломистого вороха. Игу = Рц\]/^1] ^тУ где Р2М — вероятность прохода >го компонента через второе условное решето в сепараторе ОУСЗК; 1/2у — средняя скорость относительного перемещения j-x компонентов на втором условном решете сепаратора-ориентатора; бу — время одного цикла перемещения >го компонента по второму условному решету. Вероятность Р2М представим в виде комбинации несовместных событий где P3N — вероятность >му компоненту, попавшему в желобки с шагом 5 линейчатой решётки, пройти щели шириной b на дне желобков; Р4#3 — вероятность того, что >й компонент, не попавший центром масс в щели желобков и опустившийся на боковые поверхности желобков, ориентируется в пространстве относительно щелей шириной b за счёт воздействия на >й компонент реакций боковых поверхностей гофров. Доказано [3], что для определения вероятности P4;3j процесс ориентации соломин вороха можно представить в виде комбинации двух несовместных действий: вероятности ориентации >го компонента в плоскости, параллельной поверхности решета, и вероятности его ориентации в плоскости, перпендикулярной продольной оси желобка. Тогда вероятность полного процесса Р4/3 , подразделённого на частные случаи, определяется по теореме сложения вероятностей. Для различных соотношений / (в дальнейшем /) и 5 в первом приближении вероят ность Р4/3 определяется из выражений [3] Для выражения (13) 8 > /;<06(0^ P.i3] = (1 -I, (28) (1 - а^ /90 °) + /7 /25 [1 + (1 - а^ /90°) (1 - 0кр] /(90° - arctg (3f/3z)))] Для 5 >/;<СВ(0кр^ Для S< lj< S/cosaKpj, при / < 2CB/cosaKpj < S/cosaKpj Для 5 < ^ < S/cosa^y, при !j< 2CS/cosa^y < S/cosa^y Для 5 < ^ < S/cosa^ при !j< 2CS/cosa^y < S/cosa^y 90°1 90° — arctg Для S/cosa^y < /у < 25/со5аад, при S/cosa^y < 2С5/созаад< !j 4/3; * Для S/cosa^y < !j< 25/со5аад, при S/cosa^y < 2CS/cosa^y < /у P3j — вероятность >го компонента, попавшего в желобок, достичь его стенок (^ или fi, рис. 3), Рис. 3. Схема ориентации отрезков различной длины в желобках гофрированного решета Для /у < 2S/COSOWP4,3j = 1, S df где a = arccos —, при a < 0° принимается a = 0°; arctg— — / dz угол наклона касательной стенки желобка к оси Z (рис. 3) в точке х = d/2; Zj ^ fi = fi(yb;2b); QkPj = 01ед в зависимости от формы гофры; Оед — критический угол, определяющий положение j-го компонента в плоскости, параллельной поверхности решета, при котором он под действием силы веса и реакции со стороны стенок желобка начинает разворачиваться и ориентироваться к отверстию (рис. 3), определяется с учётом его положительного значения из выражения [3]. QKpj где fj — коэффициент трения >го компонента о стенки желобка; fa — уравнение поверхности — модуль градиен- та связи в точке контакта >го компонента со связью (стенкой желобка). Координаты точек контакта концов j-x компонентов со связями (см. рис. 3) x = ^cosa, z определяется из уравнения связи fa = /(x,z), подставим в них значения х. QKPj — критический угол начала самоориентации j-x компонентов в плоскости, перпендикулярной продольной оси желобка, при 5> /(см. рис. 3) О . > arctg < ^Kpj — У - \Afx f cos arctg — + sin arctg — KyL^ cos I arctg — ± f sin I arctg — где G— сила веса >го компонента, _ 7 (8х 8х 7) 17 f 8f. 8f. , V 8fD 8fD , ) ( 8f. 8f. , V dA дЛ , ) (dz 8x 1 j^Bx Bz 7) (dx 5z 7J(dz Bx 7 J множитель связи или неопределённый множитель Лагранжа. Верхний ряд знаков для О . > arccos *ькр] — Г 1 агЛ 8х ) , в противном случае — нижний ряд знаков Координаты точек контакта концов j-x компонентов со связями можно найти из выражений |xj + |x2| = /cos0, z2 -zY = /sin0, fY =f1(x1,z1), f2 = f^(x^,z^,(23) Для случаев / > 5, когда уравнения связей Л и /2 для следующего желобка представляют собой одну кривую, величиной критического угла „ f 2A1Af1CS) 01вд < arccos —1—1—(24) Координаты точек контакта концов j-x компонентов со связями и величина СВ определяются из выражений: z2 -zi =(%i -x2)tg0!, f1(x1,z1) = 0, f2(x2,z2) = 0(25) —J—L = tg0t CB = (^ -x2) /cos©! Если кривые уравнения /j и/j в точке х = S / 2 пересекаются (см. рис. 3), то Qw< arccos (2/?vCF)/(^/7)(26) где Координаты точек контакта концов j-x из первых трёх уравнений системы (25). компонентов со связями для этого случая получим Выражение (26) справедливо для QYkpj< 90°-arccos((l / ДГ1)(дГ1 / 8х^, в противном случае применяется выражение (24). Если величина критических углов Qkpj или Q больше возможных углов j-x компонентов в этой плоскости 90° — arctg dfjdz, то отношение их в выражениях вероятности Q^90°-arctgc№) = l, Здесь Рзм определяется из условия прохода j-x компонентов, прошедших пальцевую решётку с шагом пальцев 8, через щель шириной b (вероятность прохода этих j-x компонентов щели шириной Ьбез касания её рёбер). Рассматривая процесс опускания отрезка длиной ^ на рабочую поверхность сепаратора, линейчатое решето с шагом 8, примем допущение: при опускании отрезка на линейчатую решётку его центр масс перемещается в плоскости перпендикулярно поверхности линейчатой решётки и параллельно её линиям (рис. 4), занимая различные равновероятностные положения в надрешётном пространстве, определяемые углами 0 и ф. Рис. 4. Схема возможного положения отрезка АВ в момент касания концом В плоскости линейчатой решётки Для этих условий независимые друг от друга случайные величины х, 0 и ф с равной вероятностью могут принимать значения [3]: 0<х<5; О<0<п/2; -п<ф<п (27) При этих значениях переменных отрезок длиной /у может занимать положение в пространстве, обеспечивающее проход ^ без касания линий решета с шагом 8 (проход линейного решета без касания линий линейчатой решётки и проход с пересечением одной линии); непроход отрезка !j линейчатой решётки при условии пересечения им (опускаясь центром масс в плоскости о; см. рис. 4) двух и более линий. Определено [3] общее и частное выражения вероятности одного из рассматриваемых событий 1 х2 ®2 Фг Р =----[ [ [ sinOdxt/Ot/cp (28) 4П5 xt I £ При использовании выражения (28) найдена вероятность Р2 пересечения отрезка длиной /у двух линий линейчатой решётки (для выражения (11)). Для 5 < tj< 25 7 //2 Ргз=| J (l-2x//7)dx = /7/2х + 5/2/;-1 s/2 Для 25 < /у < оо 2 5 Рг,=|J(l-2x//)dx=l-35/2/7 ^ s/2 Величина вероятности P3/lj (для выражения (13)) определится из выражения (31) в виде комби нации несовместных событий где Pv определяется из выражения (11), Р17 (д) — вероятность прохода щели шириной b без касания Р17(1)(^) или с касанием Р17(2)(^) граней гофры на дне желобка j-x компонентов, прошедших пальцевое решето с шагом 5. Для 0 < /у < b вероятность Р17 (д) пройти в щель шириной Дбез касания её граней ^ига (6) =1 - 6/26:(32) с касанием одной грани PW)(b^ = l/2b.(33) Для b< lj< оо, W = b/21,. Для b< lj< 2b, р1да1№-ь11,-1,1гь.(35) Для 2b < tj< оо, МЬ^Ър,.(36) Для определения средней скорости 1/17 и времени £ . одного цикла при перемещении j-x компонентов по поверхности клавиши ОУСЗК рассмотрим основные закономерности их перемещения при заданной закономерности движения сепаратора (см. рис. 1). При этом примем допущения: ширина и кинематика каждой соседней клавиши с шагом 5 не влияют на закономерности перемещения соломистого вороха по рассматриваемой клавише (они способствуют опусканию соломин на клавишу с равновероятностным положением в пространстве); сопротивление воздушного потока в направлении перемещения соломистого вороха вдоль клавиш не учитывалось из-за малых величин этих скоростей; перемещение слоя соломистого вороха рассматривалось как перемещение материальной точки с массой пт, при движении слоя соломистого вороха в направлении к поверхности клавиш — пропорционально первой степени проекции скорости на ось Y При анализе закономерностей перемещения соломистого вороха по клавише используем известную методологию [4]. Для относительного перемещения соломистого вороха по клавише сепаратора, совершающего движение по окружности с радиусом R (рис. 5), величина минимальной угловой скорости кривошипа (рис. 6) со = (а • f) / 2 + ^(a-f /2^ -g / /?(sina-f cosa) (37) где a = kjm, k — коэффициент пропорциональности; f — коэффициент трения соломы по ПО' верхности клавиш Рис. 5. Схема сил, действующих на соломистый ворох в момент отрыва его от клавиши Рис. 6. Схема для определения минимальной угловой скорости кривошипа клавишного сепаратора-ориентатора Начало отрыва соломы от клавиши определяется углом со^ (рис. 5). Условия отрыва со^ = arcsin (g / ^R • со2) cos a • cos у) + у где у = arctg п / со, п— частота оборотов кривошипа привода клавиш, со — угловая скорость при водного вала с кривошипом R. Рассмотрим свободный полёт соломин после отрыва от клавиш (рис. 7). Оси координат Хи /совместимы с точкой О начала отрыва соломы от клавиши, тогда на стадии подъёма траектории относительного движения соломин х = u-R -Tsina^ -^gf2)/2]sina у = (5 /а2)(1-е af)-(g /a)fcosa где В = асо • R • cos 00^ + д cos a. Рис. 7. Схема сил, действующих на соломистый ворох при его полёте Время Тмаксимального подъёма /тах при полёте соломистого вороха Т = (1 /а)1п(д/d)cosa (40) При опускании соломистого вороха Y =^тах -(g/d)cosa(f-T) + (g/a2)cosa[l-e ^Г)], (41) где /тах =(5/а2)(1-е ^)-(дТ/a)-cosa Координаты X перемещения соломин при опускании на клавишу определятся из выражения (39). Для определения точки соударения соломин вороха с поверхностью клавиши необходимо совместное решение уравнения перемещения в направлении оси Y (соломин (39) или (41)) и уравнения перемещения по оси /(система координат ХО/в точке О отрыва соломин от клавиши) поверхности клавиши сепаратора: Y = R •sin(cof1 +cot)-/? sinco^ (42) Совместное решение уравнений (39), (41) и (42) определит время t, из уравнения (39) определится координата Xсоударения. Тогда средняя скорость Ит перемещения соломин по поверхности клавиш а среднее время t . одного цикла перемещения соломин по поверхности клавиш равно времени одного оборота кривошипа tU] = 2п / со. (44) Выражения (1)—(44) позволяют оценивать вероятности прохождения сепаратора для ориентации соломин вороха при их дискретной длине 4- Учитывая, что длина !j j-vo компонента соломистого вороха — случайная в вероятностно-статистическом смысле величина, оценим вероятности Рм (11) и Р2/1 (12) реализации соответствующих событий при задаваемой плотности вероятности f (/) длины 4 соломин Рис. 8. Плотность вероятностей /(/) случайной величины / Для этих условий величины рассмотренных вероятностей будут иметь соответствующие для каждого среднего ip /то класса функции /(/), определяющие плотность вероятностей случайной величины ^(/)-С,(/,) с учётом статистической вероятности С,(/,) нахождения случайной величины / в Ам классе (рис. 9). Рис. 9. Плотность вероятности случайной величины /Р (/) Очевидно, что математическое ожидание величины вероятности w[f(^(/))J определя ется из выражения [5] ^(/)тах «IZ^C)» J pWAiW- <47> ^(/jmin При наличии зависимости f^ (/)) в виде гистограммы (рис. 9) Ш^Л1)^) (48) /=1 где / = 1,2,..., л — число классов гистограммы; С, (^) — статистическая вероятность появления случайной величины Р, (/) в Ам классе. Используя выражения (47) и (48), можно оценить усреднённые величины вероятностей ^ и ^2/1; ивеличины полноты просевания и продольной ориентации е7 из выражения (7) j-x компонентов соломистого вороха на клавишах сепаратора ОУСЗК при задаваемой плотности вероятностей f (/). Для условий 1/= 0,44 м/с, t=0,25c (закономерности клавишного соломотряса), /=2м, Ь = 150 мм, ip = 45° и различных длин соломин разработан алгоритм счёта и оценено влияние шага 8 линейчатой решётки на величину полноты просеивания £уj-x соломин различной длины через сепаратор-ориентатор (рис. 10), и для этих же условий, при 8 = 250 мм, — влияние длины / сепаратора-ориентатора на величину £; (рис. 11). —0—384 -0-336 -Д-289 -X-242 -^ 195 -о-148 Рис. 10. Зависимость полноты просевания е7j-x соломин длиной 4 через клавишный сепаратор-ориентатор (6= 150 мм, ц) = 45°, /= 2 м) от величины шага Sлинейчатой решётки клавиш: 4 = 384,17 мм, 4 = 336,95 мм, 4 = 289,73 мм, 4 = 242,5 мм, 4 = 195,28 мм, 4 = 148,06 мм Полученные закономерности £;= f (S) и £;= f (/) позволяют в первом приближении оценить основные геометрические параметры сепаратора-ориентатора соломистого вороха. —0—384 —□—336 -Д-289 -*-242 ^^195 Рис. И. Зависимость полноты просевания е7 >х соломин различной длины 4 через клавишный сепаратор-ориентатор (S = 250 мм, Ь = 150 мм) от его длины /: 4 = 384,17 мм, 4 = 336,95 мм, 4 = 289,73 мм, 4 = 242,5 мм, 4 = 195,28 мм) Выводы. Полученные стохастические выражения математической модели позволяют оценивать закономерности сепарации и ориентации соломин вороха перед их подачей на измельчитель, обеспечивая при этом условия для их качественного измельчения. Построенный алгоритм расчёта позволяет проводить параметрический синтез сепаратора-ориентатора и оценивать его основные показатели функционирования.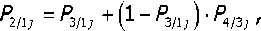
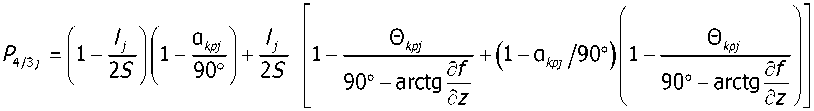
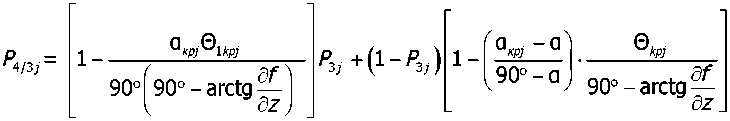
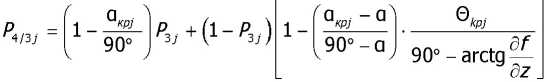
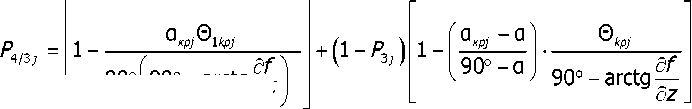
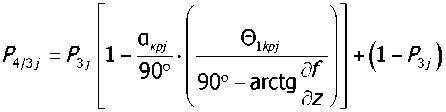
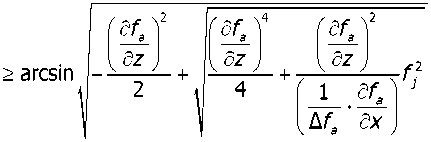
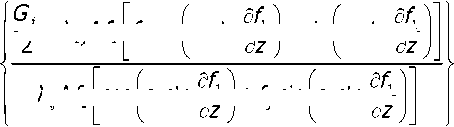
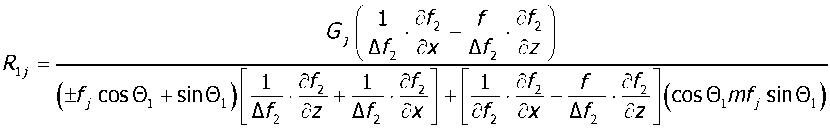
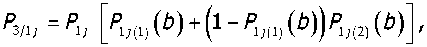
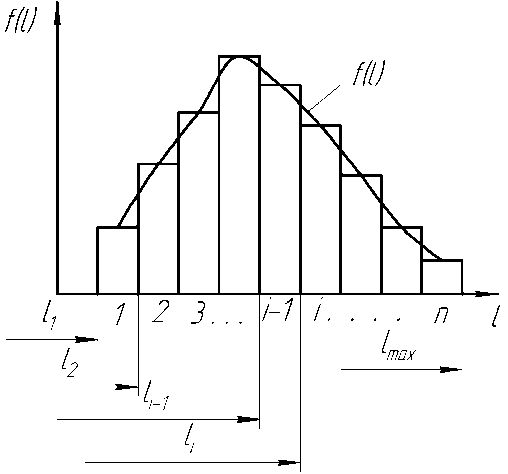
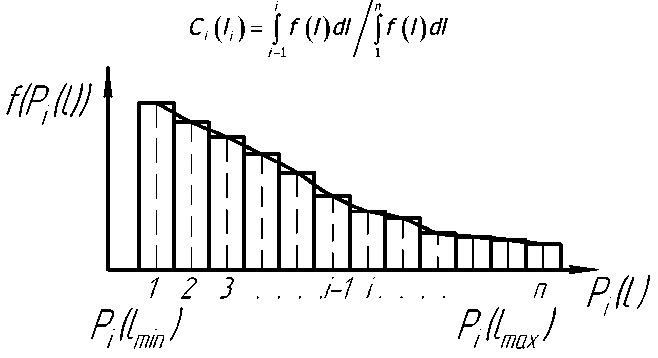
Список литературы Вероятностная модель процесса продольной ориентации стеблей соломы зерновых культур
- Эйгер, М. И. Обоснование и исследование пальцевой решётки для высокопроизводительной очистки зернового вороха/М. И. Эйгер. -Автореферат дис. к.т.н.: 05.20.01 -Ростов-на-Дону, 1970. -22 с.
- Ермольев, Ю. И. Моделирование процесса сепараций сыпучих гетерогенных сред на транспортёрном скальператоре/Ю. И. Ермольев, Г. И. Лукинов, М. В. Шелков//Известия ТГУ. -Сер. Проблемы сельскохозяйственного машиностроения. -Тула, 2004. -Вып. 1. -С. 43-52.
- Ермольев, Ю. И. Интенсификация технологических операций в воздушно-решётных зерноочистительных машинах/Ю. И. Ермольев. -Ростов-на-Дону: Изд. центр ДГТУ, 1997. -494 с.
- Долгов, И. А. Уборочные сельскохозяйственные машины (конструкция, теория, расчёт)/И. А. Долгов. -Ростов-на-Дону: Изд. центр ДГТУ, 2003. -706 с.
- Ермольев, Ю. И. Основы научных исследований в сельскохозяйственном машиностроении: учебное пособие/Ю. И. Ермольев. -Ростов-на-Дону: Изд. центр ДГТУ, 2003. -245 с.
- Григорьев, С. М. К теории плоских решёт/С. М. Григорьев//Записки ЛСХИ. -Ленинград; Пушкин, 1965. -Т. 96. -С. 171-188.


