Вероятностная оценка ресурса узлов трения и износа

При эксплуатации любых технических систем происходит старение их элементов в результате различных механических, тепловых, электрических и других физико-химических процессов, а также под воздействием внешних и внутренних нагрузок различной природы. Эти процессы и факторы вызывают накопление повреждений, развитие дефектов, необратимые изменения свойств конструкционных материалов и параметров элементов технических систем и, как следствие, постепенное снижение их функциональной способности. Это впоследствии приводит к их отказам и, в конце концов, к наступлению предельного состояния, после чего их дальнейшая эксплуатация становится невозможной [1].

Ресурс узлов трения и износа является важной технико-экономической характеристикой. При современном состоянии науки и техники возможно весьма значительное повышение ресурса узлов трения путем более грамотного подхода к их расчету и проектированию. Правильный выбор материалов и правильный расчет являются основными источниками повышения ресурса. Особое место в увеличении сроков эксплуатации занимает прогнозирование ресурса на стадии эксплуатации, когда прогнозу подлежат конкретные существующие объекты. Индивидуальное прогнозирование ресурса открывает дополнительные пути для получения экономического эффекта. На внедрение индивидуального прогнозирования требует дополнительных расходов на средства технической диагностики, разработку математических методов и программного обеспечения, позволяющих получать обоснованные выводы на основе собранной информации. Прогнозирование индивидуального ресурса включает целый комплекс задач: оценку текущего состояния объекта, прогнозирование развития этого состояния на ближайшее будущее, выдачу на основе этого прогноза рекомендаций об оптимальном остаточном сроке службы.

Техническое состояние любого изделия оценивается по значениям одного или нескольких определяющих параметров (например, степени износа или коррозии). Отказ или предельное состояние можно представить как выход определяющих параметров за пределы допустимых значений (области работоспособности) [1]. Поэтому характер изменения определяющих параметров в процессе эксплуатации позволяет вычислить технический ресурс (или срок службы) изделия и во многом рассчитать эффективность его использования.

При оценке ресурса по определяющему параметру X ( t ) (рис. 1) наиболее распространенной, в первую очередь благодаря своей простоте является линейная аппроксимация (рис. 1, а )[1...5]:

X ( t )-Х , +у t , (1)

где Х ₎ - начальное значение определяющего параметра; у - скорость изменения параметра.

Рис. 1. Изменение определяющего параметра

В этом случае оценка полного Т и остаточного ресурса

Т (после контроля или диагностики) при известном значе нии у производится решением уравнения (1) при А'- А' :

X. р- Хо np 0

T =

Y

Т= Xпр - Xk = X np -(X0 + T) YY

Величина предельного износа X определяется по условию прочности деталей, точности перемещения звеньев, требование нормативно-технической документации или исходя из требований безопасности.

Однако в большинстве практически значимых случаев линейную аппроксимацию (1) можно считать лишь грубым приближением к описанию реальных процессов. В более общей форме деградационные процессы старения и износа описываются зависимостью полиномиального вида (табл. 1) [1; 2]:

Х(t )-Х) + с 1t + c 2t2+---+с/. (3)

В этом случае оценка полного и остаточного ресурса при известных значениях коэффициентов с,с ип производится решением уравнения (3) при А '- А '(рис. 1, б ).

Несмотря на широкое использование аппроксимационных зависимостей (1) и (3), в большинстве реальных случаев монотонная зависимость определяющего параметра X от времени (или наработки) t не наблюдается. Во-первых, из-за разброса свойств конструкционных материалов и нестабильности технологии изготовления элементов начальное значение определяющего параметра X3 является случайной величиной (для него часто принимается нормальное или усеченное нормальное распределение в пределах поля допуска по закону «трех сигм»). Во-вторых, нестабильность и неопределенность условий эксплуатации и нагрузок часто приводит к случайному характеру скорости изменения определяющего параметра у в уравнении (1) или коэффициентов ср сп и показателя степени и в уравнении (3), для которых, как правило, также принимается нормальное распределение.

Тогда параметрическая модель износа или старения элемента в простейшем случае может быть описана дифференциальным уравнением [2; 5]

dX^ = * ) + h ( t ) ,              (4)

dt где y(t) - нормальная случайная величина, в общем случае зависящая от времени; h(t) - нормальный эргодический стационарный случайный процесс с математическим ожиданием цk ~ 0.

Уравнение (4) порождает случайный процесс вида X ( t ) = X 0 + j y ( t ) dt + j h ( t ) dt ,            (5)

в котором начальное значение параметра х , является неслучайной величиной для каждого изделия и случайной величиной для совокупности изделий.

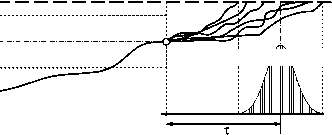
Схема формирования закона распределения ресурса элемента /Т ), при котором в результате каких-либо процессов (повреждения, износа, старения, разрегулирования и т. д.) происходит постепенное изменение определяющего параметраУ[10] показана на рис. 2.

В начале эксплуатации имеет место рассеивание начального значения определяющего параметра/X,) относительно своего математического ожиданиях, которое может быть связано с нестабильностью свойств матери алов и технологии изготовления элемента, другими внутренними и внешними причинами. Затем в процессе эксплуатации элемента определяющий параметр под дей ствием происходящих в нем процессов начинает ухудшаться (в общем случае изменение параметра может начаться через некоторый промежуток времени от начала эксплуатации, который также является случайной величиной и связан, например, с процессами накопления повреждений). Скорость изменения определяющего па раметра у зависит от природы процессов износа или старения и в общем случае также является случайной величиной. В результате всех этих процессов и явлений происходит формирование закона распределения определяющего параметра в произвольный момент времени/(X, t). Эти процессы, в частности, приводят к тому, что в момент контроля или диагностики Т наблюдается разброс значений определяющего параметра Хк совокупности изделий с распределением/Хк) и, соответственно, разброс значений полного ресурса с распределением/Т) (рис. 2, а).

х

Х нр

т

х

Хпр а    Тк

Т к б

Рис. 2. Схемы формирования полного ( а ) и остаточного ( б ) ресурсов

„Я х _к )

ЯЛТ

х , ■

А.х ,)

Разброс начального значения определяющего пара-метра/ X , ) следует учитывать при оценке ресурса неко-

Таблица 1

Устройство	Определяющий параметр X	Процесс	Математическая модель
Клапан силового цилиндра	Размер уплотнения	Изменение состояния и свойств материала под воздействием повторных переменных напряжений	NX ( t ) - cf
Торцевое уплотнение плунжерной пары насоса	Величина зазора	Механический абразивный износ	NX ( t ) - ct ”
Кран (вентиль)	Конусность	Контактная усталость рабочих поверхностей с образованием микротрещин и других дефектов	A X '( t ) - ct
Вал	Изменение диаметра вала	Окисление поверхностных слоев и разрушение окислов	NX ( t ) - c [ t + c 2 1 2
Распределительное устройство гидросистемы	Величина потока жидкости	Изменение состояния и свойств материала деталей	A X '( t ) - ct
Гидро- и пневмоцилиндры	Величина утечки жидкости или газа	Изменение состояния и свойств материала деталей	NX ( t ) - ct ”
Насос (гидромотор) гидропривода	Перепад давления	Изменение состояния и свойств материала деталей	A X '( t ) - ct ”
Двигатель внутреннего сгорания	Мощность	Изменение состояния и свойств поршневых колец (отрыв частиц горячим газом)	N X ( t ) - c 1 1 + c 2 t"
Пресс	Усилие прижатия	Изменение состояния и свойств материала деталей	NX ( t ) - ct ”
Химический реактор	Величина коррозионного износа	Коррозия материала	NX ( t ) - ct

Модели изменения определяющих параметров изделий машиностроения [7...10]

торой совокупности элементов (например, партии деталей). Для одного же конкретного элемента значение А ₀ является конкретной неслучайной величиной. Если же рассматривается поведение элемента в различных случайных режимах работы под воздействием случайных внешних факторов, то и в случае одного элемента пара-метр. А ₀ следует рассматривать как случайную величину

Примерно та же картина наблюдается при оценке остаточного ресурса по результатам контроля или диагностики элемента (рис. 2, б ). Случайный характер условий эксплуатации и нагрузок приводит к формированию распределения величины остаточного ресурса /(t) от момента контроля Т до перехода в предельное состояние.

Очевидно, что при расчете полного или остаточного

f T ) =

enT" ^{- 1} о x ( T ) + bmT m ^{- 1} [ X „p -ц х ( T ) ] --г-----:---- , „м₂ гх- --------exp^-

[ о ₀ + b exp ( mT )]² V 2 п

[ ^х np ^-ц х ^{( т} ) 1 2 1 2 о ² х ( T )

cnT " ^-1 ( о ₀ + bT^m ) + bmT m ^-1 ( X_m - X ₀ - cT " )

-------------------------------------------------- X

[ ^ 0 + b exp ( mT )]² V2 n

^X exp

1 ( X np - X 0 - cT " 2 I    о ₀ + bT^m

/

Вероятность перехода изделия в предельное состоя

ние в течение времени t может быть получена исходя из

известного соотношения [1; 6]

t

q ⁽ t ) = f f ^{( t} dt .                  (11)

В частности, для нормального закона распределения при

ресурсов детерминированными методами, в частности по формулам (1)...(3), при использовании средних значений (или математических ожиданий) величин. А , , у, с , с _п , и иХ_к определяются только некоторые их средние значения Тит (не обязательно математические ожидания). Согласно схеме (см. рис. 2, а ) становится очевидным, что к моменту Т (среднему значению ресурса, полученного детерминированным расчетом) половина из всей совокупности изделий достигнет предельного состояния, или, что то же самое, любое из них достигнет предельного состояния с вероятностью 50 %. Поэтому такая детерминированная оценка ресурса может считаться приемлемой только в тех редких случаях, когда

F (0) = 0

q ⁽ t ) = F

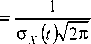
t

J ex^p'

выход из строя элемента не приводит к серьезным последствиям. В случаях когда отказ или наступление предельного

состояния могут привести к существенным экономическим потерям или возникновению аварийной ситуации, необходимо использовать вероятностно-статистический подход, при котором ресурс оценивается исходя из заданной

вероятности его исчерпания, вероятности отказа q или вероятности безотказной работы ^ .

Следует отметить, что такие задачи имеют аналитическое решение только в некоторых простейших случаях. Например, при нормальном распределении определяю

щего параметра

f ( X ) =

¹     exp J- ^[ X ^{( t ) -ц} X ^{( t )]} 2 1

о X ( t № ^р[    2о Х ⁽ t )

и линейном изменении математического ожидания ц _х ( t ) и среднего квадратического отклонения о _х ( t ) вида (1)

ц X ( t ) = X 0 + ct , о X ( t ) =о 0 + bt           (7)

с известными постоянными значениями параметров А ₀ , си с ₀ ,Ь функция плотности распределения ресурса /Т ) может быть представлена в виде [1]

f ( T ) =

c о x ( T ) + b [ X np —Ц x ( T ) ]

exp о х (т )V2n

[ X np -ц x ( T ) ] 2 2 o X ( T )

-

c ( o o + bT ) + b ( X _np - X 0 - cT ¹

( о ₀ + ьт V2n

exp

-

1 | ^X np ^{- X} 0 ^{- cT}

2 I   O 0 + bT

При нормальном распределении определяющего параметра (6) с математическим ожиданием ц _х ( t ) и средним квадратическим отклонением о _х ( t ) вида (3)

ц X ( t ) = X 0 + ct " ^, о X ( t ) =о 0 + bt m ⁽⁹⁾

с известными постоянными значениями параметров А ₀ , с , и и о ₀ , b , m функция плотности распределения ресурса /(Т) [2; 11] имеет вид

^X np ^-ц X ⁽ t ) . о X ⁽ t ) _

[ t -ц х ( t )] 2 2 ^о Х ⁽ t )

■ dt = 2 + ф ( Z ) ,

где Ф( z ) - нормированная функция Лапласа.

Оценка остаточного ресурса производится решением уравнения (11) относительно t при заданном (предельном) значении вероятности перехода изделия в предельное состояние q . Аналогичные зависимости можно использовать при вероятностно-статистической оценке ос

таточного ресурса.

Вид и параметры распределения определяющего па-раметра А ( t ), а также характер их изменения во времени в общем случае устанавливаются экспериментально (по результатам статистической обработки данных испытаний, контроля или диагностики при техническом обслуживании) или принимаются исходя из моделирования процессов, приводящих к отказам.

В качестве примера приведем гистограмму величины коррозионного износа стенок шарового резервуара для хранения бутана, бутилена и изобутилена диаметром 10,5 м емкостью 600 м ³ в течение 14 лет эксплуатации, построенная по результатам толщинометрии в 608 точках корпуса ¹ (рис. 3). Распределение хорошо аппроксимируется функцией нормального распределения с математическим ожиданием ц _х = 0,58 мм и средним квадратичным отклонением о _х =0,22 мм. Исходя из линейной зависимости коррозионного износа от времени (по ГОСТ 14249-89 [2]), начальных значений величины износа А ₀ = 0 и среднего квадратического отклонения, найденного по закону «трех сигм» по допуску на исходную толщину стенки (7), о ₀ = 0,13 мм, получим с = 0,04 мм/год и b = 0,006 мм/год.

Величина предельного износа для сосудов, работающих под давлением, рассчитывается по условию прочности. Для сферических элементов минимальная толщина стенки принимается как большее из двух значений, рассчитанных для рабочих условий и условий гидравлических испытаний [13]:

.V • min

= max

p p D ;    p _u D

4 ф [ о ] - p p ’4 ф [ о ] и - p u

’ Данные предоставлены Красноярским филиалом ООО ИКЦ «Промбезопасность».

гдерр ири - расчетное давление и давление при испытаниях, МПа; D - внутренний диаметр сферического эле мента, м; [о] и [о]и - допускаемое напряжение для материала стенок в рабочих условиях и при испытаниях, МП а; ф - коэффициент прочности сварных швов (для автома-

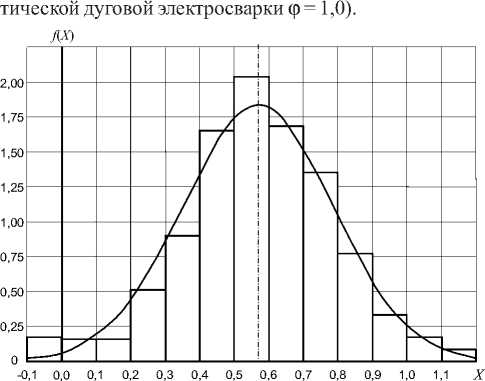
Рис. 3. Гистограмма и плотность распределения величины коррозионного износа стенок резервуара

Для заданных условий эксплуатации (s = 11,63 мм) при исполнительной толщине стенки о = 16 мм величина предельного износа A = s - s _mh =4,27 мм.

Результаты расчетов вероятности предельного состояния резервуара и оценки ресурса представлены в табл. 2 и 3. Там же для сравнения приведены результаты расчетов для случая, когда известна исполнительная толщина стенки резервуара, т. е. без учета начального разброса определяющего параметра в пределах поля допуска. При этомо ₀ = 0и 6 = оД t )/ z = 0,015 мм/год.

Например, при вероятности предельного состояния q = 0,000 1 оценка технического ресурса при о ₀ = 0,13 мм составила Т= 60 лет, при о ₀ = 0 Т= 43,4 года. Очевидно, что в условиях неполной информации необходимо принимать меньшее значение ( Т= 48 лет), так как при этом повышается гарантия работы узла. Соответственно оценка остаточного ресурса составит 29,4 года.

Таблица 2

Зависимость вероятности предельного состояния от срока эксплуатации

Срок эксплуатации Т . лет	Вероятность предельного состояния
	о 0 = 0,13 мм	О о = 0
30	-	10 " 10
40	10 " 12	10 " 5
50	10 " 7	0,0020
60	10 " 4	0,0255
70	0,0053	0,0983
80	0,0521	0,2128
90	0,1946	0,3402
100	0,4121	0,4585

Вероятностно-статистическая оценка позволяет не только более точно обосновать назначение полного или остаточного ресурсов изделия, но и дает исходные данные для анализа рисков безопасной эксплуатации (риск-анализа) и оптимизации системы технического обслуживания и управления техническим состоянием систем [5].

Таблица 3

Зависимость ресурса от вероятности предельного состояния

Вероятность предельного состояния q	Оценка технического ресурса Т , лет
	О 0 = 0,13 мм	О о = 0
10 " 9	45	32,0
10 " 8	47	33,5
10 " 7	51	35,2
10 " 6	53	37,3
10 " 5	56	40,0
0,0001	60	43,4
0,001	65	48,1
0,01	72	55,5
0,02	75	58,7
0,03	77	60,9
0,05	80	64,3
0,10	84	70,2