Вероятностно-статистическая модель бездефектности сварного соединения

Благодаря своим уникальным возможностям соединять различные конструкционные материалы, сварочные технологии широко применяются в различных сферах человеческой деятельности, формирующих большую часть (более 50 %) валового национального продукта промышленно развитых стран. Вместе с тем недостаточное качество сварных соединений относят к числу наиболее значимых причин разрушения опасных технических устройств, конструкций и сооружений.

В общем случае нормирование показателей качества сварных соединений по показателям сплошности и механическим свойствам может быть осуществлено по двум принципиально отличающимся схемам. В рамках первой схемы изначально заданными считают размеры и количество дефектов, а расчету подлежат механические свойства металла сварного соединения, предполагая, что в них могут иметь место допустимые дефекты. В рамках второй - заданными считают механические свойства металла сварного соединения, а расчету подлежат размеры и количество дефектов.

Следует отметить, что обе схемы имеют право на существование, но на разных этапах жизненного цикла изделия. В частности, первую схему следует применять на этапах проектирования, изготовления и монтажа конструкции, а вторую - на стадии эксплуатации изделия при оценке ее технического состояния и остаточного ресурса.

До недавнего времени этому вопросу не предавалось должного внимания, и большая часть норм допустимой дефектности сварных соединений основывалась на методологии второго направления с введением дополнительных ограниче- ний на размеры и количество дефектов сверху, основываясь на субъективном представлении разработчиков норм об уровне качества сварочного производства. В результате сформировался компиляционный подход, который не имеет должного научного обоснования и способствует появлению многочисленных нормативных документов, регламентирующих качество сварных соединений одно- го и того же изделия, параметры которого могут отличаться в разы.

Очевидно, что при таком количестве документации и столь отличающихся требованиях, в ней приведенных, трудно говорить о сколько-нибудь систематизированной оценке качества сварных швов.

В настоящей работе предлагается вероятностностатистическая модель бездефектности сварного соединения, которую следует использовать при разработке методов нормирования показателей качества в рамках первого направления.

Согласно [1] сварную конструкцию следует рассматривать как целостную совокупность упорядоченно взаимодействующих элементов, в которой прочность на уровне сварного соединения достигается при соблюдении условия

aij ^ acj ( rh );

Fk ^ Fck ( acj ) ,

где a_ij , a_cj - соответственно текущее и критическое значения технологических несовершенств j -го типа; F_ik , F_ck - соответственно текущее и нормативное значения j -й характеристики механического свойства металла сварного соединения.

Для решения (1) в первую очередь необходимо определиться с математической моделью бездефектности сварного соединения, используя которую можно рассчитать a cj ( R_h ) и F_ck ( a cj ) . Для определения вида функции бездефектности сварного соединения введем по аналогии с [2] вероятностную модель появления k дефектов одного типа в эталонной области сварного соединения М 0 , предполагая, что в каждый фиксированный момент времени t они образуют пуассоновские ансамбли (многомерные пуассоновские потоки, размерность которых равна размерности области М 0 ):

X к (t)

Q k ( t )      М ехр ^[—^X t ) ] .                  ⁽²⁾

к !

Здесь X ( t ) - математическое ожидание числа дефектов одного типа в области М 0 в момент времени t .

Согласно (1) за предельное состояние сварного соединения с к дефектами j -го типа примем событие, для которого выполняется условие a_i >  а с хотя бы для одного дефекта в пределах области М 0 . Тогда надежность есть вероятность отсутствия в области М 0 дефектов больше критической величины.

Использование вероятностных моделей типа (2) для решения задачи о бездефектности сварного соединения предполагает независимость а_с от величины нагрузки. Применительно к (1) это требование не актуально, так как условия нагружения учитываются здесь при определении нормативных требований к показателям механических свойств F ck .

Далее в (2) следует ввести ограничение по размеру дефекта, а именно: из всего множества дефектов, размещенных в области М 0 , необходимо оставить только те, размеры которых превышают а с . Для преобразования вида Q ( t ) ^ Q ( а с , t ) воспользуемся процедурой разреживания, заключающейся в удалении из ансамбля части элементов. Возможность применения этой процедуры следует из предельной теоремы теории вероятностей для редеющих потоков [3], которая гласит, что если стационарный пуассоновский поток с интенсивностью X последовательно подвергать независимым преобразованиям (случайному преобразованию, при котором каждое событие исходного потока независимо от других событий остается с вероятностью q и исключается с вероятностью p ), то результирующий поток будет сходиться по вероятности к простейшему пуассоновскому потоку с интенсивностью X . Опуская промежуточные математические преобразования, они приведены в [2], запишем окончательное выражение вероятностной модели размещения в области М 0 к дефектов размером больше а_с :

,      . Xк (ас, t)

Q k ( а с , t ) =----, ,     ехр ^[-X ( а_с , t ) ] .          (3)

к !

Расчет по (3) при к = 0 представляет собой определение вероятности отсутствия в области М ₀

дефектов больше критической величины, т. е. Q ( а с , t ) = P ( а с , t ). В общем случае, когда в области М могут иметь место несколько типов дефектов, выражение для Р ( а с , t ) имеет вид:

^Р ( а с , t ) = ехр ^- L j ^X ( ^aсj , t ) dM , _ i = j М          M 0 _

где X ( a_сj , t )

-

математическое ожидание числа дефектов, размер которых больше а^; а^ - критическая величина дефекта j-го типа; М - общая протяженность сварного шва, представленная в виде суммы эталонных областей.

Выражения типа (4) достаточно широко используются в качестве математической модели надежности сварного соединения [2, 4, 5], в которой не достаточно полно учитываются технологические особенности изготовления сварных металлоконструкций. Исследователи, как правило, предполагают, что математическое ожидание количества дефектов есть величина постоянная. В действительности выборочный неразрушающий контроль и ремонт дефектных участков сварного соединения, приводят к изменению X ( а с -, t ) на соответствующих участках, а следовательно, и во всей области М .

Для учета этих особенностей выделим из области М контролируемые участки сварного шва и разделим их на две группы. К первой группе отнесем участки сварного соединения, на которых отсутствуют недопустимые дефекты - Р ( а_с ) для них считается равной единице. Ко второй группе отнесем участки с недопустимыми дефектами, для которых Р ( а_с ) меньше единицы.

Согласно общепринятой практике, все отремонтированные (исправленные) участки сварного соединения подлежат повторному контролю в объеме 100 %. Из этого следует, что вероятность обнаружения недопустимых дефектов при условии их наличия должна быть равна единице. Однако это предположение не всегда верно, так как методы неразрушающего контроля характеризуются определенной достоверностью и реально можно говорить об отсутствии недопустимых дефектов с какой-то долей вероятности. К тому же ремонт дефектных участков не всегда обеспечивает выполнение условия Р (ас ) = 1, так как ремонтные работы оказывают влияние на механические свойства металла сварного соединения, а следовательно, и на величину ас, которая является нижним пределом интегрирования при определении Р (ас). Учитывая эти обстоятельства, модифицируем (4), для чего разобьем область М на участки с постоянными значениями X( а^) и ас и примем, что на момент ввода конструкции в эксплуатацию Р(ас, t) = Р(ас). Далее предположим, что в пределах области М взаимодействие участков сварного шва соответствует схеме с последовательным соединением элементов, которая с точки зрения надежности сварного соединения является наиболее консервативной и поэтому вполне оправданной в условиях неопределенности. Для принятой схемы взаимодействия участков сварного шва его надежность можно рассчитать как:

P ( a c ) = P nc P c P cr , (5)

Для упрощения выражения (5) выразим М_nc и М c через общую длину сварного шва и объем неразрушающего контроля. Эта процедура не представляет сложности, так как интегрирование по длине шва есть суммирование эталонных областей. Тогда, с учетом принятых допущений, а также формул (5)-(9) выражение для Р ( a c ) мож-

где P_nc , P c , P cr - вероятности отсутствия дефектов размером больше критической величины на неконтролируемом, контролируемом и отремонтированном участках сварного шва соответственно, рассчитываемые по формулам:

но представить как

{ П ,

-Е (1- V •Р(D]acj)) X j=1

г . /    \ dM \

^{X J К} c ^{( a} cj )_м Г , М M 0 JJ

ⁿ           dM

Рnе = ехр -Е J Кnc (acj )— ;

j = 1 М nc          M 0

nc

n    M

^Р c = ехр Ь Е J ^К c ( а с, ) — j = 1 М c         M 0

c

* ^dM

J Кcr ( acj ) M

M_cr         M 0

^Р еr = ехр

n

- Е J К j =1 М cr

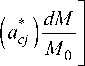
Здесь К nc , К _c , К cr - математические ожидания числа дефектов размером больше критической величины на неконтролируемом, контролируемом и отремонтированном участках сварного шва соответственно.

На стадии проектирования изделия конструктор не обладает информацией о количестве и длине отремонтированных участков, а также о влиянии ремонтно-восстановительных работ на a cj , что создает неопределенность в отношении Р_сг . Для ее раскрытия примем, что при разработке технологии ремонтно-восстановительных работ будет соблюдено условие «равнопрочности» исходного и отремонтированного участков шва по всей номенклатуре механических свойств. В таком случае можно допустить, что a c, = а * , а P cr = P c и вклю-

где V - величина объема неразрушающего контроля, равная отношению длины проконтролированных участков к общей длине шва.

В связи с тем, что значения a cj для разных категорий сварных швов могут быть разными, для определении Р ( a c ) лучше всего использовать не математическое ожидание числа дефектов больше a_cj , а математическое ожидание количества дефектов всех размеров К ₀, которое не зависит от a cj . Для этого воспользуемся известным соотношением между К ( a_c j ) , плотностью функции распределения размеров дефектов f ( a j ) и К ₀ j [1]:

J

^К ( ^a cj ) = ^К 0 j J ^f ( ^a j ) ^da j а_сj

Подставив (11) в (10) и выполнив необходимые математические преобразования, получим выражение для вероятности бездефектности свар-

ного соединения

Р (ac ) = ехр -

n

- Е j=1

K0j(1 - V • Р (D/ acj))

чить исправленные участки сварного шва в состав проконтролированных бездефектных.

Вероятность отсутствия на проконтролированных участках шва недопустимых дефектов связана в основном с достоверностью используемого

X J J f ( a j ) da j dM Г .

М a c j                      I

метода контроля, которую можно выразить через условную вероятность обнаружения дефектов размером больше а с, .

Учитывая это обстоятельство, выражение для Р_c примет вид

Ре = ехр \ ^- Е J ^{[ 1 - Р} ( D ^а с ) ] ^К c ( ^a cj^ dM Г , ⁽⁹⁾ I j = 1 M c                           ^M 0

c

где Р ( Dja_C j ) - условная вероятность обнаружения дефектов j -го типа размером больше a_c j .

Стохастическая природа технологической дефектности представлена в (12) через функции распределения размеров дефектов и математического ожидания их количества, а эффективность неразрушающих методов контроля через произведение V • Р ( D/a_c j ) . Так, например, при a cj <  a ₀ j , где a ₀ j -минимальный размер выявляемого дефекта j -го типа, Р ( D/a_c j ) = 0 и вероятность отсутствия в сварном соединении дефектов определяется состоянием технологического процесса сварки и не зависит от объема неразрушающего контроля. При Р ( D/a_c j ) и V , отличных от нуля, надежность

сварного соединения возрастает в зависимости от

их значений. В предельном случае, когда Р ( D(а с ) = 1,0 и V = 1,0 величина Р ( а с ) не зависит от М , f ( a j ) и Х ₀ j , т. е. при любом a j величина Р ( а с ) = 1,0 .

В рамках сложившейся системы проектирования металлоконструкций обеспечение прочности сварного соединения в составе конструкции только за счет (1) наталкивается на значительные вычислительные трудности. Поэтому для снижения размерности таких задач часто используют метод декомпозиции, предполагающий разукрупнение исследуемого объекта ( C w ), в данном случае на сварные соединения ( e W ) и узлы (p i ):

n ( m )

C w = U P i l U e j I . (13) i = 1 V j = 1 )

Исходя из двухуровневой декомпозиции обеспечение работоспособности конструкции на стадии проектирования следует осуществлять в два этапа. На первом этапе решается вопрос о прочности сварного соединения посредством выбора основного и сварочного материалов, а также назначения категорий ответственности сварных соединений, для которых предварительно рассчитываются показатели их качества по допустимой дефектности и механическим свойствам.

На втором этапе выполняется расчет на прочность и долговечность элементов сварных конструкций, для которых считаются заданными механические свойства, геометрические характеристики и количество допустимых дефектов в сварном соединении.

Нормирование характерных размеров дефектов осуществляется посредством решения (12) относительно aCj для случая, когда V = 0, а М = М0, т. е. без учета фактической длины сварного соединения и объема его контроля. Это связано с тем, что определение длины сварного шва, характера его нагруженности, объема и методов контроля осуществляется на втором этапе проектирования конструкции и учесть их изначально не представ- ляется возможным. В то же время известно, что влияние параметров V и М на вероятность бездефектности сварного соединения (12) существенно и пренебрегать им нельзя. Не нарушая логики (13), это можно сделать за счет соответствующего коэффициента надежности, введя его в уравнение предельного состояния сварного соединения.

В заключение отметим, что выражение (12) позволяет с единых теоретических позиций решить задачу нормирования технологических несовершенств сварных соединений (определить a_C j ), учитывая, с одной стороны, нормативные требования по бездефектности, а с другой - возможности технологического процесса сварки, находящегося в стабильном и статистически управляемом состоянии.