Вероятностно-статистические модели ликвидности рынка недвижимости

Для решения задач, связанных с определением ликвидационной стоимости, анализом качества залоговой массы банков, установлением стартовой цены на торгах, разработкой стратегий инвестирования, и других задач требуется объективный анализ уровня (степени) ликвидности активов. Ликвидность имущества характеризуется тем, насколько быстро объект можно продать по цене, адекватной рыночной стоимости на открытом рынке. В связи с этим основной характеристикой ликвидности объекта является срок, в течение которого объект недвижимости, выставленный на продажу по цене, равной рыночной стоимости, будет продан. Этот срок, называемый сроком (временем) экспозиции, зависит от стечения многих заранее неизвестных продавцу факторов: от того, когда появится заинтересованный покупатель, как он оценит преимущества и недостатки объекта, устроит ли цена продавца и сможет ли он договориться с ним о цене, которая его устроит. В то же время срок экспозиции объекта зависит от позиции продавца, от того, как продавец оценивает шансы объекта быть проданным по выставленной им цене, насколько продавец заинтересован в быстрой продаже, готов ли он снижать первоначальную цену и т. п. Поэтому срок экспозиции является случайной величиной, а уровень ликвидности объекта обычно характеризуют типовым сроком экспозиции.

При этом однозначного определения типового срока в официальных документах нет, однако на практике чаще всего говорят о среднем сроке экспозиции (см. [1]).

Следует отметить, что такая характеристика во многих ситуациях не является достаточно информативной и не позволяет решать многие практические задачи. Так, например, не вводя дополнительные предположения относительно вероятностного распределения времени экспозиции, информации о среднем сроке недостаточно, чтобы решить задачу прогнозирования потока доходов, которые можно ожидать при продаже квартир во вновь построенном многоквартирном доме. Отсутствие более полной информации о распределении сроков экспозиции предметов залога не позволяет прогнозировать поступление доходов от продажи банками залоговой недвижимости и полноценно оценивать риски, связанные с проблемами при продаже. Этой характеристики недостаточно, чтобы контролировать, как меняется ликвидность во времени, поскольку, чтобы определить средний срок экспозиции, в общем случае требуется достаточно много времени, существенно превышающего этот срок. Эти и другие задачи могут быть успешно решены, если оценщик не ограничен информацией о типовом сроке экспозиции, а располагает моделями и набором требуемых статистических характеристик, отражающих вероятностные свойства процессов продажи на рынке недвижимости. Поскольку рынок недвижимости имеет вероятностный характер, а срок экспозиции является случайной величиной, модели ликвидности рынка недвижимости должны основываться на теории вероятностей, а процедуры определения характеристик ликвидности – на методологии статистического вывода.

Большинство отечественных публикаций и методических разработок, связанных с ликвидностью активов, посвящены методам определения ликвидационной стоимости. Однако с точки зрения развиваемого в настоящей работе подхода большее значение имеют работы по дескриптивному анализу рыночных данных, позволяющему обнаружить и интерпретировать зависимости срока экспозиции от различных факторов. Поэтому остановимся на анализе публикаций, посвященных статистическому исследованию рынков недвижимости более подробно.

Из работ этого направления прежде всего следует выделить исследования рынков недвижимости с использованием больших массивов рыночной информации, направленные на выявление закономерностей и зависимостей ликвидности от различных факторов. В работе словенских специалистов [2] на основании анализа рыночных данных выделены три группы факторов, которые являются статистически значимыми детерминантами ликвидности:

• 1)    характеристики собственности;

• 2)    рыночные условия;

• 3)    макроэкономические параметры.

Время нахождения на рынке объекта недвижимости зависит от его характеристик, заявленной начальной цены, финансовых и общих экономических условий. Особую роль играют рыночные условия. В работе на основе анализа статистики показано, как более высокие цены на жилье и средняя процентная ставка по кредитам удлиняют срок нахождения недвижимости на рынке, в то время как более высокая доступность жилищных кредитов сокращает этот срок. Время на рынке определенной недвижимости также варьируется для различных сегментов микрорынка. При этом относительная важность каждой группы факторов различна. Наиболее важными факторами, определяющими время экспозиции в наблюдаемый период, являются стоимость объекта и доступность финансирования жилищного строительства, а также индекс цен на жилье. В целом в работе представляют интерес методы анализа рыночных данных, которые могут найти применение при исследовании зависимости ликвидности от различных факторов.

В работе [3] на основе анализа выборки из 1,3 миллиона наблюдений в Германии представлены доказательства того, что энергоэффективность и экология стали наиболее значимыми факторами принятия решений арендаторами и покупателями на европейских рынках жилья за последние годы, что оказывает заметное влияние на ликвидность объектов.

Большое влияние на ликвидность жилья оказывает общий уровень экономики. Анализ рыночных данных, представленный в работе [2], позволил установить зависимость уровня ликвидности на рынке жилой недвижимости, измеряемого средним временем продажи, от общей активности рынка, который, в свою очередь, зависит от состояния экономики.

В статье приведены результаты исследования факторов, влияющих на время нахождения объекта на рынках жилой недвижимости в странах Центральной и Восточной Европы. Степень завышения цен оказалась наиболее значимой детерминантой времени на рынке. Более высокие цены на жилье (на национальном уровне) и средняя процентная ставка по жилищным кредитам продлевают время нахождения объекта на рынке, в то время как более высокая доступность жилищных кредитов, напротив, сокращает объем. Анализ ликвидности для арендного жилья в семи крупнейших городах Германии с использованием технологии больших данных и модели пропорциональных рисков Кокса приведен в работах [4, 5]. На больших объемах данных автор иссле- довал зависимости ликвидности от возраста жилья, количества комнат и расстояния до центров городов.

Следует отметить ряд работ, авторы которых, основываясь на рыночной статистике и используя алгоритмы машинного обучения, предлагают эффективные технологии определения ожидаемых сроков экспозиции (см., например, [6]). Методы прогнозирования сроков экспозиции для конкретных объектов недвижимости, основанные на анализе характеристик домов и геосоциальной информации о месте ее нахождения, рассмотрены в работах [7, 8], в которых приведены результаты анализа реальных данных о продаже недвижимости, собранных в Пекине, подтверждающих, по мнению авторов, эффективность предлагаемого ими подхода для измерения ликвидности на рынке недвижимости.

В работе [7] развиваются технологии машинного обучения для исследования ликвидности, в частности, предложены методы прогнозирования сроков экспозиции объектов недвижимости. Основу методов представляет многоцелевое обучение на основе регрессии. Приведены результаты статистических исследований жилой недвижимости в Пекине, демонстрирующие эффективность предложенных процедур. Зависимость времени экспозиции недвижимости от детерминантов, таких как процентная ставка, возможность трудоустройства и т. п., которые характеризуют общее состояние экономики, исследуется в работе [8].

В отечественной литературе до последнего времени отсутствовали работы по статистическому анализу ликвидности на рынках недвижимости. Наиболее полный анализ ликвидности недвижимости, находящейся в городах России с численностью более миллиона человек, включая Москву и Санкт-Петербург, основанный на обработке рыночных данных, содержащих несколько миллионов историй объявлений о продажах недвижимости из различных сегментов, приведен на ресурсе открытого доступа [9]. Представленные на сайте гистограммы и кумулятивные распределения сроков экспозиции позволяют увидеть характер вероятностных распределений и сопоставить вероятностные свойства ликвидности для разных городов и разных сегментов рынка недвижимости. Приведенные результаты исследований показывают, как ликвидность зависит от сегмента (подсегмента) рынка недвижимости, от места положения объектов и их размеров. Также следует отметить работу [10], в которой представлен статистический анализ спроса на рынке недвижимости, в значительной степени определяющего ликвидность. В добавление к указанным работам следует указать документ Ассоциации банков России [11], в котором содержатся рекомендации по сбору и анализу рыночных данных, необходимых для оценки ликвидности объектов недвижимости.

Отдельно следует выделить материалы, в которых рассматриваются модели, развиваемые в другой сфере – в теории выживаемости. Так, в работе [12] по аналогии с теорией выживаемости вводится функция, имеющая смысл вероятности того, что событие произойдет в некоторый малый период времени при условии, что оно не произошло до начала этого периода. В качестве такого события рассматривается совершение сделки, а функцию называют функцией риска (термин взят из теории выживаемости). Далее вводится экспоненциальная зависимость этой функции от параметров рынка. При этом предполагается, что функция риска от времени не зависит. Таким образом, автор приходит к известной модели Кокса, на основе которой он проводит статистическую обработку рыночных данных. Такой подход позволяет извлечь из данных много полезной информации, в том числе зависимости показателя ликвидности от различных факторов. Тема моделирования ликвидности объектов недвижимости с использованием теории выживаемости, получившей развитие в последние годы в различных прикладных работах по статистике, обсуждается в другой чрезвычайно инте- ресной работе [13], в которой показано, что, если при определении статистических характеристик срока экспозиции (среднего срока и т. д.) использовать только данные об объектах, с которыми были зафиксированы сделки, то получается заниженная оценка. Авторы предлагают процедуры оценки, основанные на методологии, развиваемой в рамках теории выживаемости. Эта методология позволила повысить точность прогнозов и обеспечить динамичное реагирование на изменяющиеся рыночные условия.

Приведенные публикации показывают выраженный тренд в направлении новых подходов, ориентированных на создание вероятностно-статистических моделей и методов анализа и оценки ликвидности рынка недвижимости и технологий, способствующих их применению на практике.

Подводя итог этому краткому анализу, следует отметить, что в настоящее время вероятностная теория ликвидности еще не разработана. Отдельные публикации свидетельствуют о том, что мы находимся в начале пути к созданию такой теории. Однако, как это часто бывает в период становления прикладных наук, нет необходимости создавать эту теорию с нуля. Подобные задачи легко могут быть решены, если воспользоваться разработанной во второй половине прошлого столетия методологией анализа случайного времени до того, когда произойдет некоторое событие. Поскольку своим развитием эта теория обязана проблемам, связанным с анализом и оценкой вероятностных характеристик времени безотказной работы технических систем, эта теория получила название «теория надежности». Другое направление, которое также оказало значительное влияние на развитие методов анализа и прогнозирования случайных процессов такого типа, известно как теория выживаемости биологических объектов. Также модели такого типа активно используются в теории массового обслуживания (теории очередей).

В настоящей статье развивается общий подход к теории ликвидности рынка недвижимости, основанный на вероятностно-статистических моделях. Основу предложенных моделей составляют результаты анализа большого объема рыночных данных о продажах недвижимости в городах России. Предложенное описание позволяет системно взглянуть на ликвидность рынка недвижимости и обеспечить решение ряда задач, которые могут повысить эффективность управления недвижимостью. Специфическая для теории вероятностей и статистического вывода терминология и основные положения развиваемой теории ликвидности изложены наглядно и «просто, насколько это возможно, но не более того» (А. Эйнштейн).

1.    Вероятностное распределение сроков экспозиции

Содержательное описание рынка недвижимости как вероятностной (стохастической) системы приведено в работах [1, 14]. Жизнь объекта на рынке начинается после того, когда объявление о его продаже чаще всего появляется на одной или нескольких электронных досках объявлений. Каждое объявление обычно содержит краткую характеристику объекта недвижимости и цену, по которой продавец хотел бы продать принадлежащее ему имущество (цену предложений). Далее в случайные моменты времени в течение периода, пока объявление находится на доске объявлений, с этим объявлением знакомятся потенциальные покупатели. Просмотры требуемых объектов недвижимости покупатель начинает с формирования фильтра, с помощью которого он отбирает только объекты, представляют для него интерес. После более глубокого знакомства с объектом покупатель принимает решение о целесообразности его покупки. В случае покупки объект снимается с продажи. В противном случае он остается на доске объявлений, «ожидая» следующих покупателей. Естественно, чем больше покупателей в течение заданного времени посмотрят объявления, тем выше вероятность того, что объект будет продан, и тем короче в среднем период до сделки.

С точки зрения вероятностного подхода объект недвижимости можно считать ликвидным, если объект будет продан за требуемое (достаточно короткое) время с высокой степенью вероятности. Если же вероятность продажи в требуемые сроки маленькая, то следует говорить о низкой ликвидности. Для расчета таких вероятностей следует построить математическую модель процесса покупки, адекватно учитывающую вероятностную природу рынка.

Общее представление о сроке экспозиции τ как случайной величине можно составить, используя функцию распределения вероятностей F( t ), которая показывает, какова вероятность того, что срок экспозиции объекта недвижимости будет меньше, чем некоторое заданное время t :

F( t ) = P ( τ < t ), (1)

где τ – срок (время) экспозиции объекта (от времени появления объекта на рынке до момента заключения сделки), выраженное в количестве дней;

P (...) – вероятность события, обозначенного в скобках.

Другими словами, функция распределения F( t ) имеет смысл вероятности того, что объект, выставленный на продажу, будет продан в течение срока, равного t. Тогда вероятность того, что объект не будет продан в течение этого срока, равна:

Q( t) = P ( т >  t) = 1 - F( t ). (2)

Функцию Q(t), отражающую динамику продаж во времени и показывающую среднее количество объектов в относительных единицах (по отношению к первоначальному количеству), которые останутся непроданными за заданное время t, назовем функцией ликвидности. Эта функция при t = 0 равна единице и монотонно уменьшается со временем. То есть если принять за единицу количество выставленных на продажу гомогенных объектов, то со временем часть объектов оказываются проданными, а количество оставшихся объектов монотонно убывает, стремясь к нулю.

Также для описания случайной величины используется плотность распределения f( t ), которая является производной от функции распределения. Математическое ожидание случайного срока экспозиции Т , которое может интерпретироваться как типовой срок экспозиции, записывается в следующем виде:

те

T = E ( t ) = J t f ( t ) dt . (3) 0

В ряде публикаций показано, что формула, связывающая функцию ликвидности с типовым сроком ожидания, может быть представлена так:

T = J Q ( t ) dt .                                (4)

Также в качестве характеристики ликвидности объекта может использоваться другой параметр – время (срок), в течение которого объект будет продан с заданной вероятностью γ , равный гамма-процентному квантилю распределения срока экспозиции.

Еще одна временна ́ я характеристика заслуживает особого внимания для описания ликвидности – интенсивность продаж, равная отношению плотности распределения времени экспозиции объекта в некоторый момент времени к вероятности того, что объект до этого времени не будет продан:

X( t ) = f( t ) / Q( t ),                                  (5)

где f( t ) – плотность распределения вероятностей случайной величины (времени экспозиции);

Q( t ) – функция ликвидности.

Интенсивность продаж является динамической характеристикой, она показывает, как меняется ликвидность объекта, измеряемая параметром λ(t), во времени.

Выражения (1)–(5) составляют основу вероятностного описания ликвидности. Основываясь на таком описании, можно моделировать различные стратегии продаж, предсказывать потоки доходов от продажи объектов недвижимости с указанием вероятности, что такие доходы действительно поступят в указанное время, определять возможность продажи за короткое время большого количества различных объектов недвижимости и рассчитывать риски, связанные с недостаточной ликвидностью активов

2.    Экспоненциальный закон ликвидности

Анализ поведения интенсивности продаж в процессе жизненного цикла объявления о продаже позволяет понять, каким будет распределение срока экспозиции объекта. Действительно, из уравнения (5) следует, что интенсивность продаж связана с функций ликвидности Q( t ) следующей формулой:

∞

Q ( t ) = exp -J Я ( t ) dt . L ^Jc

Выражение для показателя степени экспоненты в уравнении (6) называют кумулятивной функцией риска. Из приведенной формулы видно, что функция ликвидности зависит от того, как ведет себя интенсивность продаж λ ( t ) во времени. Наибольшее распространение в задачах, связанных с анализом времени до наступления некоторого события (в данном случае в качестве такого события выступает продажа объекта или сдача его в аренду), получил закон Вейбулла с интенсивностью вида:

X (t ) = Л x m x t ™ ^- 1 , (7)

где m и Λ – числовые параметры, которые могут быть определены из анализа статистических данных.

Основываясь на предположении относительно интенсивности продаж, заданном в виде соотношения (7), можно записать выражения плотности распределения сроков экспозиции, а также для закона распределения и функции ликвидности:

f( t) = Л x m x t m ^-1 x exp(- A t ™ ); (8)

F( t ) = 1 – exp(- Λ t ^m ); (9)

Q( t ) = exp(- Λ t ^m ). (10)

Конкретные значения параметров распределения m и Λ характеризуют вид распределения Вейбулла и соответственно функции ликвидности. Параметр Λ определяет масштаб распределения. В зависимости от его значения кривая распределения сжимается или растягивается по переменной. Соответственно, также ведет себя функция ликвидности.

Параметр m характеризует форму распределения. При значении m , равном единице, интенсивность продаж не меняется во времени, а функция ликвидности выражается экспонентой с показателем степени Λ . Такое имеет место, если в течение всего цикла жизни объявления сохраняется постоянный и уравновешенный спрос на объекты недвижимости конкретного сегмента (подсегмента) и поток потенциальных покупателей сохраняется постоянным (стационарным), а условия продажи не меняются.

При значении m , меньшим единицы, интенсивность продаж снижается во времени. Обычно это имеет место, если в начальный период после появления объявления наблюдается повышенный интерес к объекту, который затем медленно спадает со временем. Этому, в частности, может способствовать то, что в течение времени объявление о продаже занимает более низкие позиции на электронной доске объявлений, уступая место более новым объявлениям. При этом шансы, что покупатели обратят на него внимание, постепенно снижаются.

И, наконец, при значении m, большем единицы, интенсивность продаж со временем возрастает. При этом плотность распределения приобретает вид, близкий к плотности логнормального распределения с выраженным максимумом, а при определенных значениях параметров переходит в нормальное. Функция ликвидности характеризуется медленным снижением в начальный период «жизни» объявления. Такая динамика характерна, например, для ситуации, когда помещения в строящемся объекте продаются по постоянной цене. В этом случае активность покупателей возрастает по мере приближения к завершению строительства, когда риск замораживания стройки снижается.

Не следует думать, что реальный рынок строго соответствует одной из этих моделей. Как и всякие модели, они лишь приближенно описывают процессы продажи и могут использоваться только как некоторое приближение при анализе ликвидности рынка недвижимости. Каждая модель имеет свою область применения и свои ограничения. Поэтому для более корректного описания процессов продажи в некоторых случаях на разных этапах жизненного цикла объекта на рынке можно использовать разные модели. Обоснованием использования той или иной модели для анализа ликвидности может служить только неформальный анализ рыночных процессов, соединенный со статистическим анализом рыночных данных.

Особый интерес при описании характеристик ликвидности рынка недвижимости представляет случай, когда параметром формы является m = 1. В этом случае интенсивность продаж не зависит от времени:

λ ( t ) = Λ . (11)

В случае постоянной интенсивности продаж выражение для функции ликвидности принимает вид:

Q( t ) = exp(- Λ t ). (12)

Из формулы (12) следует, что плотность распределения сроков экспозиции также подчиняется экспоненциальному закону, которая может быть записана так:

f( t ) = Λ exp(- Λ t ).                           (13)

Таким образом, если принять допущение о том, что интенсивность продаж не меняется во времени, то функция ликвидности, характеризующая вероятность того, что объект недвижимости не будет продан в течение заданного времени, описывается экспонентой с показателем, равным интенсивности продаж. Отсюда легко получить формулу для математического ожидания срока экспозиции:

те

T = J Q ( t ) dt = 1 / Л .                     (14)

Модель экспоненциального закона успешно используют в различных приложениях, в частности в теории надежности для вероятностного описания случайного времени до возникновения отказов в технических системах, и других приложениях. При этом в теории надежности Λ называют интенсивностью отказов, а в публикациях по теории выживания – функцией риска, поскольку она показывает вероятность наступления события в ближайший период при условии, что такое событие не наступило до начала этого периода, а под событиями понимают наступление катастроф.

Тот факт, что интенсивность продаж не меняется со временем, интуитивно понятен из анализа процессов продажи объектов недвижимости. Действительно, шансы продать объект, который уже некоторое время находился на доске объявлений, такие же, как у другого такого же объекта, который только что выставлен на продажу. Другими словами, вероятность того, что объект недвижимости будет продан в ближайшем периоде, не увеличивается от того, что объект долгое время уже находился на рынке, то есть плотность распределения оставшегося срока экспозиции при условии, что до этого времени событие (сделка) не состо- ялось, остается такой, какой была в начале наблюдения. И это свойство характерно только для экспоненциального распределения (в отличие от большинства других распределений, например нормального или логнормального, для которых характерно увеличение интенсивности со временем).

Есть еще одно объяснение, почему срок экспозиции на установившемся конкурентном рынке во многих случаях можно описывать экспоненциальным законом. Рассмотрим процесс покупки объекта после появления объявления о его продаже. Потенциальные покупатели, приходящие на рынок, образуют стационарный пуассоновский поток (если исключить сезонную составляющую). Количество покупателей, появляющихся в заданный период времени, является случайной величиной, подчиняющейся закону Пуассона с параметром, который зависит от периода времени и не зависит от времени, когда этот период начался. При таких предположениях время между приходами покупателей подчиняется экспоненциальному закону. Отсюда следует, что и время до появления первого покупателя, готового купить объект недвижимости при заданных условиях, также подчиняется экспоненциальному закону. Так мы опять приходим к экспоненциальному распределению времени (срока) экспозиции. Здесь, однако, следует сделать одну оговорку. Дело в том, что о постоянной интенсивности продаж можно говорить только по истечении некоторого времени после появления объявления на рынке. В короткий период в начале продажи эти условия обычно нарушаются. Появившееся на доске новое объявление, как правило, характеризуется повышенным вниманием покупателей. Однако в первые недели в большинстве случаев требуется, чтобы продавец и покупатель согласовали свое решение и оформили сделку. В это время объявления зачастую остаются на доске, и факт совершения сделки не фиксируется. Следующие недели интенсивность, наоборот, возрастает, поскольку начатые ранее сделки завершаются. И только по прошествии нескольких недель ситуация обычно выравнивается, процесс появления заинтересованных покупателей и, соответственно, интенсивность продаж становятся постоянными. Более подробно вопрос о поведении интенсивности продаж в первый период жизненного цикла объявления о продаже будет обсуждаться далее в связи с анализом рыночных данных.

Практическое использование теории возможно только тогда, когда используемые вероятностные модели будут адекватны реальным рыночным данным, а приведенные характеристики могут быть определены на основе рыночной статистики, поэтому в следующем разделе рассматриваются методы анализа рыночных данных и их связь с уже приведенными вероятностными характеристиками.

3.    Статистические (эмпирические) характеристики ликвидности

От вероятностных характеристик случайной величины – срока экспозиции следует отличать их статистические (эмпирические) аналоги. Именно статистические аналоги, рассчитанные на основе рыночных данных, позволяют в полной мере понять экономический смысл соответствующих характеристик.

В этом разделе рассматриваются статистические аналоги приведенных ранее вероятностных параметров и приводятся расчетные формулы для их определения на основе рыночных данных. Чтобы облегчить восприятие приведенных формул, статистические характеристики обозначаются так же, как соответствующие вероятностные характеристики.

Перед тем, как обсуждать методы оценки параметров ликвидности, рассмотрим некоторые особенности статистических данных, которые следует учитывать при обработке данных и интерпретации результатов. Прежде всего надо отметить, что, как правило, информация о фактических датах начала продажи и завершения ее сделкой скрыта от исследователя рынка недвижимости, однако имеется возможность мониторить даты появления и снятия объявлений о продажи. В настоящей статье принимается допущение о том, что объект недвижимости снимается с публикации по причине его продажи. Другими словами, предполагается, что период экспозиции объекта недвижимости равен сроку жизни на электронной доске соответствующего объявления о продаже объекта. Такой подход к исследованиям ликвидности на рынке недвижимости рекомендован Методическими рекомендациями по анализу ликвидности объектов недвижимости для целей залога [11], разработанными рабочей группой Комитета Ассоциации российских банков и рекомендованными для применения Решением Комитета по залогам и оценке. Там же отмечено, что такое допущение вполне оправдано, поскольку в большинстве случаев объявление действительно снимается только в случае продажи объекта. К таким же выводам приводят исследования, проведенные автором настоящей статьи на отдельных типах недвижимости, краткие результаты которых изложены далее. К этому следует добавить, что информация о сроках жизни объявлений является доступной в отличие от прямой информации, относящейся к сделкам. С учетом изложенного приведенные далее результаты статистического анализа сроков жизни объявлений ассоциируются со сроками экспозиции объектов, и вероятностные свойства, характеризующие время жизни объявления, распространяются на сроки экспозиции объекта. В связи с этим в статье термины «срок жизни объявления» и «время экспозиции объекта» используются как синонимы.

Вторая особенность связана со способом сбора требуемой рыночной информации. В отличие от ситуации, когда данные получаются из активного планируемого эксперимента, здесь мы имеем дело с наблюдениями, которые начинаются с некоторого момента времени после того, как объявления уже «прожили» часть своей жизни.

При этом известны моменты их появления, которые могут значительно отличаться у разных объектов. Далее в процессе наблюдения появляются новые объявления, и случайным образом снимаются старые и появившиеся в период наблюдения новые объявления. В некоторый фиксированный момент формируется выборка данных, включающих сведения о сроках жизни объектов, снятых с продажи, и объявлений, которые на этот момент оказываются непроданными. Таким образом, в выборку включаются не только данные об объектах, которые к моменту исследований были проданы и, значит, относительно них известно точное время экспозиции, но и объекты, которые на этот момент не были проданы. Сформированная таким образом выборка называется цензурированной. В настоящей статье рассматриваются статистические характеристики и методы их получения, соответствующие условиям, когда все наблюдаемые объекты проданы, и выборка сформирована только из данных о проданных объектах. Анализ таких данных позволяет более понятно интерпретировать смысл статистических характеристик и их связь с соответствующими вероятностными параметрами ликвидности.

В соответствии с изложенным рассмотрим следующий план наблюдений. Группа объектов недвижимости в количестве N единиц, относящихся по функциональным характеристикам к одному сегменту рынка и расположенных на ограниченной территории, выставлена на продажу в одинаковое время. Следует отметить, что допущение о том, что объекты выставлены на продажу в один момент времени, не имеет существенного значения. Здесь важно, что значения времени экспозиции каждого объекта измеряются от момента появления соответствующего предложения о продаже объекта недвижимости на доске объявлений, который на вторичном рынке обычно разный.

Предполагается, что все объекты выставлены на продажу по корректно уста- новленным рыночным ценам, поэтому можно считать, что сроки экспозиции каждого объекта образуют однородную выборку из одного вероятностного распределения. Наблюдение за этими объектами продолжается до тех пор, пока не будут проданы все объекты. В процессе мониторинга последовательно фиксируются даты продажи каждого объекта и определяются сроки его экспозиции (от времени появления на рынке до момента продажи), выраженные в количестве дней:

τ ₁, τ ₂,… τ _i , …, τ _N .                            (15)

Пусть по истечении времени t были проданы N_t объектов. В этом случае статистическая (эмпирическая) вероятность того, что любой объект, принадлежащий этому сегменту, будет продан за время t , оценивается как частота продаж сопоставимых объектов в течение этого времени:

F( t ) = N_t / N ₀.                              (16)

Фиксируя данные о состоявшихся продажах всех выставленных на продажу объектов для различных значений t , можно восстановить статистическую функцию F( t ) на всем периоде наблюдений.

Соответственно, статистическая вероятность того, что объект не будет продан в течение времени t , рассчитывается по формуле:

Q( t ) = 1 – N_t / N ₀ = ( N ₀ – N_t ) / N ₀ = K_t / N ₀, (17) где K_t = N ₀ – N_t – количество оставшихся (непроданных) за время t объектов.

Построенную таким образом функцию Q( t ) для различных временны ́ х интервалов в соответствии с введенными ранее определениями можно интерпретировать как эмпирическую функцию ликвидности.

Статистический аналог математического ожидания (среднее время экспозиции) при таком плане наблюдений определяется как выборочное среднее:

N

^T = n J ^T i .                         (1⁸⁾

Отметим, что выборочное среднее (18) является наилучшей (в смысле минимума среднеквадратической ошибки) оценкой математического ожидания в классе линейных оценок. Таким образом, используя выборку данных по всем состоявшимся продажам (15), можно восстановить функцию ликвидности Q( t ), построить гистограмму (статистический аналог плотности распределения) и рассчитать выборочное среднее, являющееся оценкой математического ожидания срока экспозиции. Кроме того, основываясь на принятой модели и определенных таким образом характеристиках, можно определить гамма-процентный квантиль распределения сроков экспозиции, который характеризует период времени, в течение которого объект недвижимости будет продан с заданной вероятностью, например, 95 процентов.

• 4.    Эмпирическая интенсивность продаж и коэффициент емкости рынка

Особого внимания заслуживает статистический аналог интенсивности продаж (эмпирическая интенсивность), который также может быть определен на основании рыночных данных. Эмпирическая интенсивность продаж определяется как количество продаж в единицу времени из общего количества объектов, оставшихся непроданными к определенному моменту, и рассчитывается по формуле:

X( t) = n ( t , t + △ t) / ( K t x △ t ),                (19)

где n ( t , t + Δ t ) – количество объектов, проданных в течение интервала [ t , t + Δ t ];

[ t , t + Δ t ] – интервал времени, в течение которого определяется количество сделок (обычно принимается равным неделе или месяцу);

Kt – количество объектов, оставшихся непроданными ко времени t из числа всех объектов, первоначально выставленных на продажу.

Эмпирическая интенсивность продаж имеет понятный экономический смысл. Если в качестве интервала [ t , t + Δ t ] принять единичный период времени, например одну неделю или один месяц, то этот параметр совпадает с коэффициентом емкости рынка, который определяется как количество объектов, проданных за этот период, деленное на общее количество единиц, находящихся на рынке в ожидании покупки в начале этого периода (см. [16]). Коэффициент емкости является одной из наиболее значимых характеристик рынка. Он относится к определенному периоду жизни объекта на рынке и позволяет отслеживать, как меняется активность процессов продажи объектов недвижимости во времени. По этой причине определение емкости рынка в процессе анализа рынка является важным требованием Федерального стандарта оценки «Оценка недвижимости (ФСО № 7)». Полезно отметить, что при постоянной во времени интенсивности продаж соотношение (14) сохраняется для эмпирических аналогов интенсивности продаж и среднего срока экспозиции и может быть использовано для приближенного определения среднего срока через коэффициент емкости рынка.

Следует отметить, что интенсивность продаж как характеристика гомогенных активов позволяет сформулировать введенный Ю.В. Козырем критерий К 1 в вероятностной трактовке (см. [17]). В соответствии с такой версией этот критерий может быть сформулирован следующим образом: гомогенные объекты, характеризующиеся бо ́ льшим значением интенсивности продаж более ликвидны, чем объекты с меньшей интенсивностью продаж.

Если вернуться к вероятностно-статистической теории, то коэффициент емкости рынка, близкий по смыслу к интенсивности продаж, может рассматриваться как среднее количество продаж в единицу времени, отнесенное к общему количеству объектов, имеющихся на рынке в исследуемом сегменте к определенному моменту. Это, однако, справедливо только при малых интервалах времени (более строго – при Δt, стремящемся к нулю).

• 5.    Статистический анализ рыночных данных. Подтверждение экспоненциального закона ликвидности

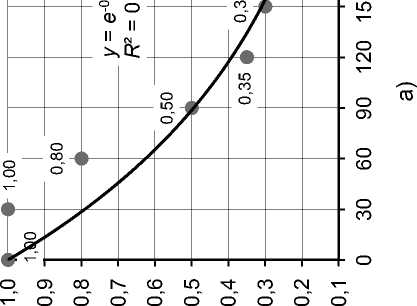
Как уже было показано, срок экспозиции является случайной величиной, подчиняющейся экспоненциальному закону распределения. Это заключение было сделано на основе принятых допущений и качественного анализа процессов покупки на конкурентном рынке. Однако для того чтобы эту модель рекомендовать для практического использования, требуется подтвердить адекватность модели на основе рыночных данных и предложить методы определения параметров этих моделей на основе рыночных данных. С этой целью командой специалистов ООО «Информ-оценка» были обработаны статистические данные, касающиеся сроков экспозиции для объектов недвижимости различных сегментов в городах России [9]. Представленные далее результаты обработки рыночных данных позволяют сделать некоторые выводы относительно распределения сроков экспозиции. На графике (рис. 1) показана доля объектов, которые остаются непроданными в течение отмеченного по оси абсцисс времени * . Зависимость доли непроданных объектов во времени, как уже было указано, является эмпирической функцией ликвидности. Здесь и на других графиках (рис. 2–4) координата по оси абсцисс измеряется в днях.

Из приведенного на рисунке 1 графика видно, что в целом эмпирическая функция

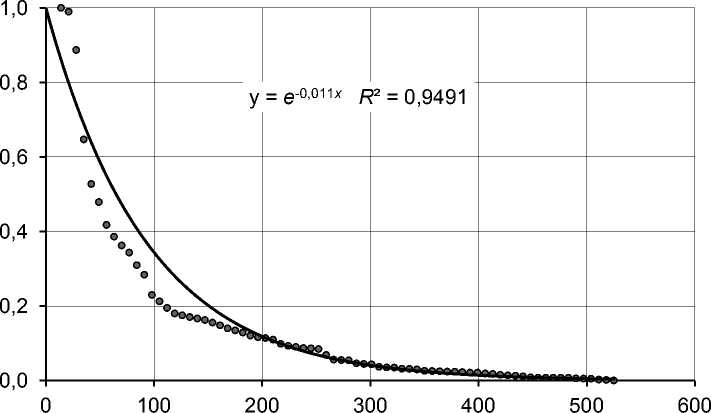
Рис. 1. Функция ликвидности. Офисные помещения. Нижний Новгород

ликвидности достаточно хорошо приближается к экспоненциальному распределению. Однако при более тонком анализе кривой можно увидеть два эффекта:

1) начальный период, первые три недели, практически все объекты остаются непроданными (доля непроданных объектов остается близкой к 1);

• 3) по прошествии этого периода доля оставшихся непроданными объектов более быстро снижается, обгоняя зависимость, которая следует из экспоненциальной модели.

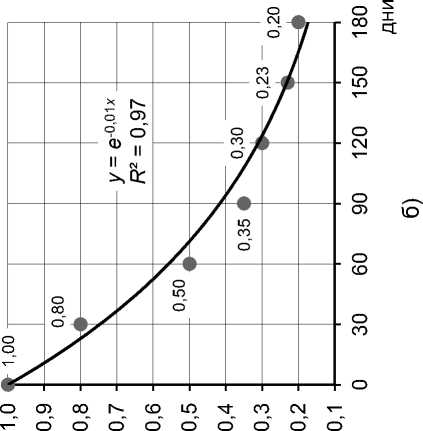
Указанные эффекты легко объяснить, проведя анализ процессов покупки на рынке недвижимости. Первые три-четыре недели уходят на согласование условий сделки, ее оформление и дополнительно включают время, которое объявление может находиться на доске объявлений после завершения сделки. Рост интенсивности продаж в последующие два-три месяца связан с окончательным завершением сделок, начатых в первый месяц, и более высокой активностью покупателей, которые присутствовали на рынке в ожидании подходящих предложений. Далее ситуация стабилизируется, и объект «ожидает» появления новых покупателей, заинтересованных в его приобретении. Этот период, который может длиться много месяцев, ха- рактеризуется постоянной интенсивностью продаж. Если первый месяц исключить из рассмотрения, а последующий период разделить на два этапа (на рисунке 2 выделены различными маркерами), каждый из которых моделировать своим распределением, то модели сроков экспозиции будут более точными.

Сопоставляя два графика (рис. 1 и рис. 2), можно увидеть, что при отдельном рассмотрении каждой из двух частей качество комбинированной модели заметно повысилось.

Интересно проследить за поведением во времени коэффициента емкости рынка, имеющего смысл статистического аналога интенсивности продаж.

На приведенном на рисунке 3 графике видно, что в первые недели интенсивность продаж растет (отмечены треугольниками). Далее наблюдается падение (отмечены квадратиками), и по истечении двух-трех месяцев после выставления объекта на продажу (круглые маркеры) интенсивность продаж, измеряемая коэффициентом емкости рынка сходных объектов, стабилизируется и, если исключить сезонный тренд и другие внешние факторы, влияющие на рыночную ситуацию, сохраняется практически постоянной в течение дальнейшего периода жизни.

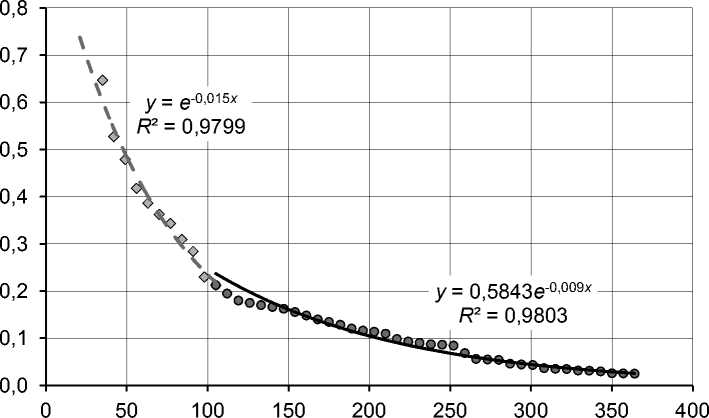
Рис. 2. Функция ликвидности. Офисные помещения. Нижний Новгород (начальный период обозначен квадратиками)

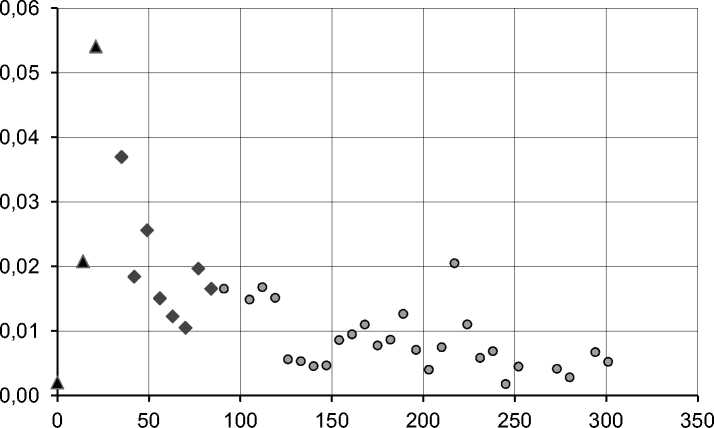
Рис. 3. Интенсивность продаж. Офисные помещения. Нижний Новгород

Такой же характер зависимости функции ликвидности наблюдается и в других сегментах рынка.

Приведенный на рисунке 4 график показывает, что в начальный период (ромбовидные маркеры) (по прошествии первых недель) интенсивность более высокая, а после двух месяцев функция ликвидности хорошо аппроксимируется экспонентой (круглые маркеры). Особо следует сказать о первых неделях после выставления объекта на продажу. Как уже отмечалось, первые 2–4 недели после появления объявления практически не снимаются с доски объявлений, а следующие 4–8 недель снимаются более активно, что свидетельствует о более высокой интенсивности продаж в первые два месяца после выставления объекта недвижимости на открытый рынок. По истечении этого периода интенсивность продаж стабилизируется и остается постоянной в течение последующего времени. В этот период жизненного цикла выставленного на продажу объекта функция ликвидности может быть описана экспонентой с интенсивно-

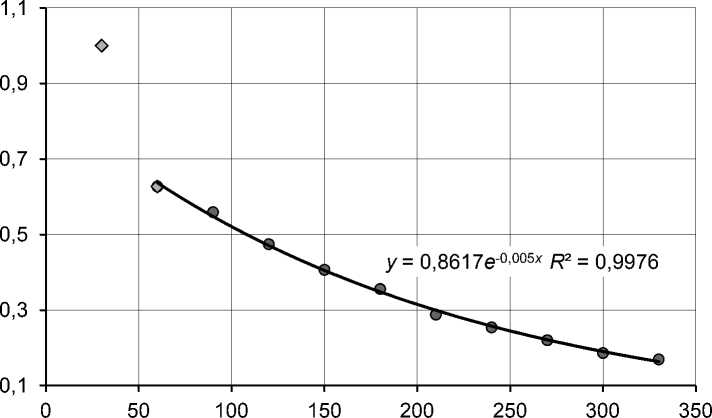
Рис. 4. Функция ликвидности. Земельные участки. Москва

стью продаж ( Λ ), равной 0,005 день^-1, что может быть интерпретировано следующим образом: в среднем 0,5 процента объектов из общего количества объектов конкретной группы, находящихся в продаже, будут проданы в течение одного дня. Напомним, что эта величина является обратной среднему значению экспозиции. Отсюда, зная интенсивность продаж, легко определить средний срок экспозиции. В рассматриваемом случае Т = 1 / 0,005 = 200 дней. Отметим, что прямой расчет среднего срока экспозиции по данным выборки приводит примерно к такому же результату, что является еще одним подтверждением адекватности модели.

Приведенные примеры можно рассматривать как иллюстрацию основных положений теории, изложенной в предыдущих разделах. Обоснованием справедливости предложенных моделей и возможности практического применения экспоненциального закона для описания сроков экспозиции объектов недвижимости могут служить комплексные исследования рынка недвижимости, проведенные специалистами ООО «Информ-оценка» в 2019–2021 годах.

Исходные данные для исследований – сведения о сроках экспозиции различных объектов недвижимости в городах Мо- скве и Санкт-Петербурге, а также во всех городах России с численностью более 1 миллиона человек. Были обработаны несколько миллионов объявлений о продаже коммерческой недвижимости, жилья и земельных участков. Все данные были разделены по сегментам и подсегментам рынка, по классам и типам объектов, а также по ценовым зонам в пределах каждого из исследуемых городов. В результате такой стратификации образовались сотни страт, представляющих однородные выборки. Объем каждой выборки колебался в достаточно широких пределах: от нескольких сотен до нескольких тысяч объектов. Для каждой такой выборки были построены статистические (эмпирические) функции ликвидности, являющиеся дополнением до единицы кумулятивных гистограмм частотного распределения сроков экспозиции (17). Также определены средние значения сроков экспозиции для каждой из образованной указанным способом выборки.

Результаты масштабного исследования реальных сроков экспозиции объектов различных сегментов недвижимости в городах России размещены в интер-нет-ресурсе открытого доступа [9]. Результаты некоторых из проведенных исследований представлены на рисунках

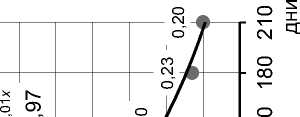
Ki_rotf

Ki_rotf

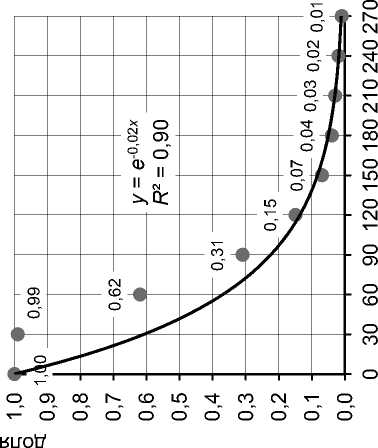
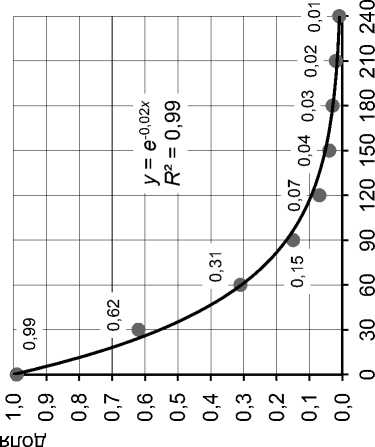
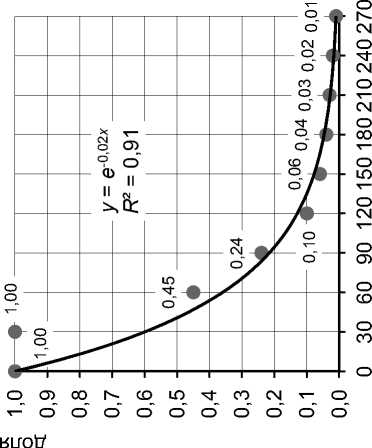
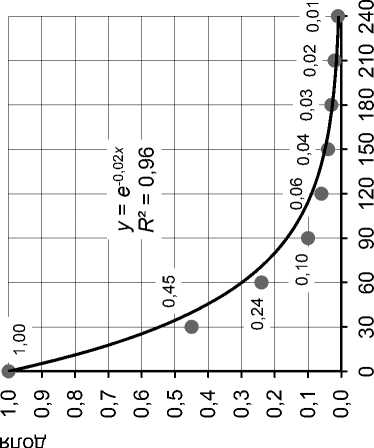
Рис. 5. Санкт-Петербург                         Рис. 6. Москва                        Рис. 7. Нижний Новгород

(многоквартирная жилая застройка, объекты (многоквартирная жилая застройка,            (промзона, производственно свободного назначения, 418 объектов) торговая недвижимость, 906 объектов) складская недвижимость, 60 объектов)

5–7 * . На графиках 5а, 6а и 7а видно, что в первый месяц сделки не фиксируются, по крайней мере практически все предложения сохраняются на досках объявлений. После исключения первого месяца (рис. 5б, 6б, 7б) зависимости, построенные по тем же данным, имеют четко выраженный экспоненциальный характер. Таким образом, приведенные графики показывают, что отмеченные ранее свойства кривой ликвидности проявляются для разных сегментов недвижимости в различных городах и территориальных зонах России.

Заключение

В работе предложена новая концепция анализа ликвидности объектов недвижимости, основанная на вероятностно-статистических моделях сроков экспозиции. Показано, что в первом приближении при решении задач, связанных с ликвидностью, можно в большинстве случаев опираться на экспоненциальный закон ликвидности. В процессе работы над статьей у автора сложилось твердое убеждение, что применение вероятностно-статистических моделей обогатит методологию анализа рынка недвижимости и обеспечит решение многих задач эффективного управления объектами недвижимости, которые ждут своего решения. К сожалению, теория вероятностей и анализ данных пока не находят должного понимания в среде практикующих оценщиков. Сегодня программы подготовки оценщиков не предусматривают развитие вероятностного мышления, что сдерживает создание новых более эффективных методов анализа рынков объектов недвижимости и определения их стоимости. Дальнейшее развитие теории видится в направлении перехода к более сложным моделям распределения сроков экспозиции, учитывающих более тонкие эффекты процессов продажи, прежде всего перехода к трехпараметрическому зако- ну Вейбулла с переменной интенсивностью продаж. Одновременно следует разрабатывать адекватный инструментарий анализа данных о сроках экспозиции, основанный на широком использовании машинного обучения с учетом особенностей мониторинга рынка недвижимости и планов сбора исходных данных.

Выражаю благодарность сотрудникам ООО «Информ-оценка», которые выполнили большой объем работы по анализу статистических данных, лишь небольшая часть результатов которой отражена на приведенных в статье графиках. Особую благодарность выражаю кандидату технических наук Н.П. Баринову, доктору экономических наук Ю.В. Козырю и доктору экономических наук С.А. Смоляку, ценные замечания и рекомендации которых помо гли мне подготовить эту статью.