Вероятностное моделирование управляемого хаоса

Управляемый хаос (Controlled Chaos, от греч. chaos - «беспорядок, неразбериха, путаница») является начальным звеном разрушительной триады, включающей также гибридную войну (Hybrid

Warfare) и цветные революции (Coloured Revolution), которая достаточно активно изучается сегодня как в России, так и за рубежом [1]. Противоборство сторон в рамках данной триады соответствует условиям игры с антагонистическими интересами фон Неймана [2] и имеет целью не столько торжество каких-либо морально-этических или правовых норм, в том числе узаконенных на межгосударственном и общечеловеческом уровне, сколько захват или разрушение жизненно важных национальных пространств противника: географического, природно-энергетического, идеологического и информационного [3].

С позиций теории сложных систем (СС) и системного анализа управляемый хаос представляет собой объект, соответствующий области исследования нерефлекторных СС, определение которых было дано Н.Н. Моисеевым применительно к СС социально-экономического, экологического, военного и др. типа [4; 5]. Нерефлекторные СС отличаются нелинейной динамикой и неустойчивым поведением, эффекты самоорганизации сочетаются в них с наличием хаотических режимов и полифуркациями, характерным и неотъемлемым свойством является «человеческий фактор» (далее без кавычек) - в виде лиц, принимающих решения (ЛПР), а также множеств других людей, прямо или косвенно участвующих в реализации принятых решений [6-9]. Анализ и моделирование хаотических процессов, протекающих в нерефлекторных СС, имеют для них -в рамках упомянутой триады — жизненно важное значение как в теоретическом, так и в практическом плане.

По взглядам на динамику хаоса представители разных наук [10-13] заметно различаются между собой: разброс терминов, субъективных мнений и высказываний на этот счет говорит о том, что переход от аксиологических знаний ЛПР к верифицированным (более подробно см. далее) здесь еще не произошел. Не претендуя на существенный вклад, ограничимся замечанием, что изучение хаотических процессов, на наш взгляд, требует комплексного применения методов и средств исследования СС с целью создания систем управления (СУ) ими — в этой связи представляется важным слабоструктурированные и трудно формализуемые задачи, относящиеся к плохо организованным (диффузным) нерефлекторным СС, делать понятными для компьютера, переводить на язык формул и алгоритмов, к чему не все ЛПР, разумеется, сегодня готовы.

Цель статьи - обсуждение подходов, принципов и результатов теории хаоса, а также теории СС и СУ, связанных с применением современных способов моделирования: от мысленного и вербального до компьютерного метода статистического имитационного моделирования (СИМ), в интересах изучения и управления хаотическими процессами в нерефлекторных СС.

Проблема управления хаосом

Классическая схема СУ включает объект и субъект управления, а также систему информационного обмена между ними [7-9]. Теория управления располагает аксиомами, без которых работа СУ считается невозможной [4; 5; 8]. Эти аксиомы требуют выполнения условий наблюдаемости и управляемости объекта; наличия цели и критерия оценки эффективности управления; свободы выбора управляющих воздействий; наличия ресурсов (методов и средств), обеспечивающих работу СУ. На вопрос о том, в какой мере хаотические процессы в нерефлекторных СС соответствуют аксиомам управления, утвердительного ответа теория хаоса, развитая применительно к физическим СС, разумеется, не дает. В то же время не только ряд терминов: таких как «аттрактор», «фрактал», «фактор», «неопределенность», «вероятность», но и формальные принципы анализа и моделирования хаотических процессов могут быть перенесены в проблему управления хаосом [10-13].

Аналогичным образом дело обстоит и с теорией знаний, на основе которой формируется здесь онтологическая модель ситуации (ОМС). Напомним, что онтологией (от греч. ontos - «сущее») именуется совокупность понятий (концептов) и отношений между ними в рассматриваемой предметной области [6]. Персональные онтологии основаны на индивидуальных знаниях ЛПР, групповые онтологии формируются из их фрагментов путем достижения взаимопонимания между ЛПР и представляют собой ОМС как концептуальную платформу для достижения поставленной общей цели. Поэтому в составе ОМС присутствуют как явные верифицированные знания, признаваемые всеми ЛПР, так и их неявные аксиологические знания (в виде убеждений, личного опыта и гипотез), остающиеся предметом дискуссии между ними. Сегодня есть все основания считать, что именно аксиологические знания, при условии их полноты, логической связанности и непротиворечивости, обладают наибольшим потенциалом для управления нерефлекторными СС [8].

Причина этого в том, что для успешных действий ЛПР необходимо не столько достоверное описание тех или иных объектов и процессов, сколько знание дела как руководство к обоснованному выбору этих действий, что заставляет их «наводить мосты», находить и расширять точки соприкосновения между аксиологическими и верифицируемыми знаниями о рассматриваемых СС. Формируемая на основе верифицированных знаний ОМС предполагает применение объек-

a

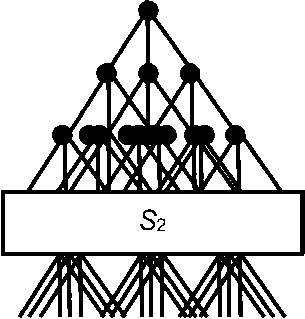
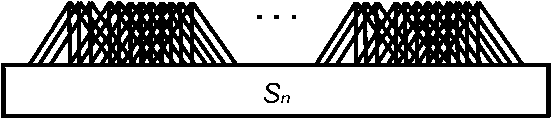
Рисунок 1. Вероятностная модель неуправляемого хаотического процесса

тивной теории вероятностей (ТВ) Лапласа — Колмогорова, тогда как ОМС, создаваемая на базе аксиологических знаний ЛПР, имеет в виду применение субъективной ТВ Бернулли — Сэвиджа. Эти два подхода и две системы «вероятностных координат» различаются по существу - как, например, системы декартовых и сферических координат в геометрии. Поэтому, пользуясь ими, разные ЛПР способны принимать решения и предпринимать управленческие действия, которые заметно различаются между собой.

Принципы моделирования хаотического процесса

Будем считать, что дерево решений в обобщенном виде включает три ветви: связанные с ухудшением, сохранением и улучшением прежнего состояния СС. Тогда последовательный переход от общего состояния СС ^ к состоянию S2, а затем — к Sn будет иллюстрировать схема, приведенная на рисунке 1, а, где точки ветвления (полифуркации) обозначены черными кружками. Очевидно, что при переходе от 51 к Sn число три-адных ветвей возрастает достаточно сложным (поскольку ветви пересекаются и накладываются друг на друга), но предсказуемым образом — если результаты полифуркации можно считать детерминированными (что, однако, представляется нереальным), и непредсказуемым образом - если они являются стохастическими. В последнем случае ОМС демонстрирует существенный рост неопределенности знаний ЛПР о состоянии СС, ее свойствах, характеристиках и рабочих параме трах, что даже визуально отражает сгущение ветвей при движении «сверху вниз» на рисунке 1, а.

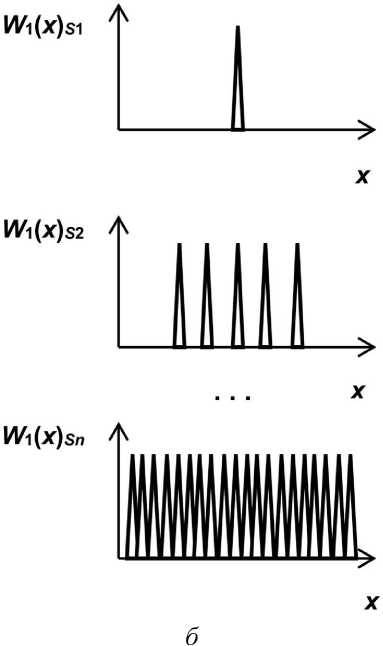
Рассматривая иерархические деревья, аналогичные приведенному на рисунке 1, а в перевернутом виде, Л. да Винчи предположил, что суммарная толщина его ветвей на любой высоте будет равна толщине основного ствола [10] - на языке ТВ это соответствует условию сохранения для 5^ S₂ ... S_n вероятности полной группы событий, равной единице. В соответствии с этим модель неуправляемого хаотического процесса отражает схема на рисунке 1, б, где ^i(^)si;52> -финитные функции одномерной плотности распределения вероятности (ПРВ) случайной величины х (фактора, параметра СС), соответственно, для 5р 5₂ и S_n, которые в условном (дискретном и ненормированном) виде показаны острыми треугольниками. Видно, что сгущению ветвей при движении «сверху вниз» на рисунке 1, а здесь соответствует «уплотнение» композиции исходной ПРВ — при переходе к S₂ в виде конечного числа ^(х^р а при переходе к S_n, если и » 1 - в виде «квазибесконечного» их числа.

Отметим, что для более реалистичных непрерывных ПРВ рост неопределенности ведет к равномерному закону для W^x)^ в соответствии с принципом безразличия Лапласа, согласно которому все состояния СС при отсутствии необходимой информации о них считаются равновероятными.

Моделирование управляемого хаотического процесса иллюстрируют схемы на рисунке 2: если ЛПР удастся удержать процесс перехода

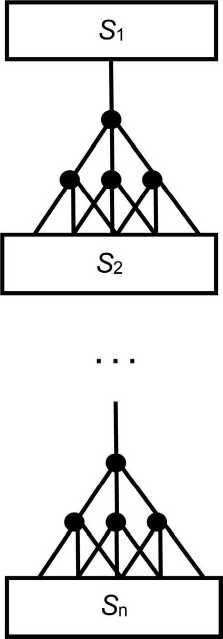
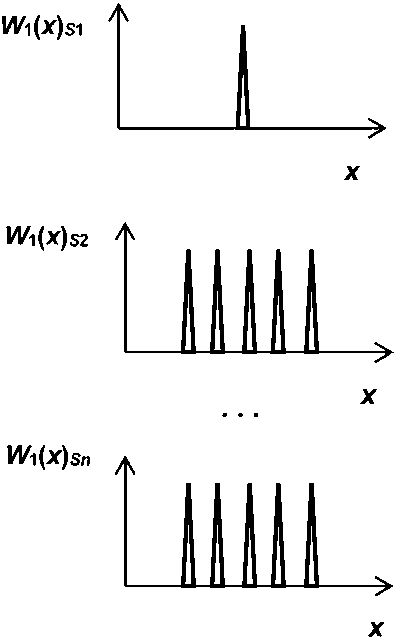
Рисунок 2. Вероятностная модель управляемого хаотического процесса от 5] к Sn от неограниченного роста числа три-адных ветвей (которое на рисунке 2, а принято равным пяти), то все ПРВ Wx(x)sn ..^(х)^ на рисунке 2, б будут соответствовать композиции показанных пяти И^х)^. Вопрос, удастся ли ЛПР сделать это на практике, возвращает нас к теории управления нерефлекторными СС: от аксиом управления до методов и средств реализации способов управления конкретными СС, в том числе с применением метода СИМ.

Типовые аналитические модели

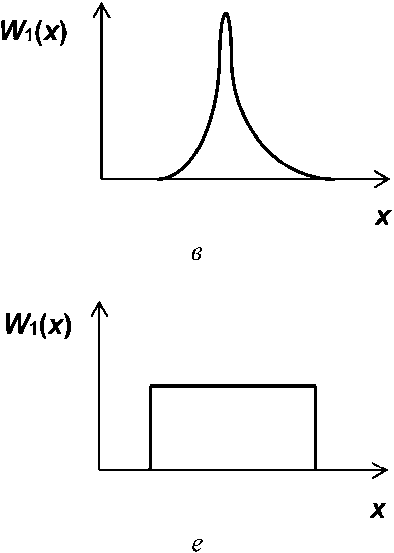
Модели ТВ, соответствующие росту неопределенности знаний ЛПР при движении «сверху вниз» на рисунках 1 и 2, демонстрирует рисунок 3. Первым предельным случаем здесь является полная определенность знаний, когда ПРВ W, (х) = 8(х), где 6(т) - дельта-функция Дирака, см. рисунок 3, а. Второй предельный случай -равномерное распределение РК^х), соответствующее принципу безразличия Лапласа, см. рисунок 3, е. Варианты реализации других моделей иллюстрируют рисунки 3, б—д.

В условиях применимости обобщенной центральной предельной теоремы (ЦПТ) ТВ финитная модель, показанная на рисунке 3, в, принадлежит семейству одномерных устойчивых законов [8; 18] и в существенной области преобразования Фурье л:^;^]; /7[0;[/Д определяется через характеристическую функцию (ХФ) вида y_v(U) = expUaU-

-б|Г|^1 + лЛ7/|Г|)С(Г;у)]},    0)

где [/-аргумент ХФ; ос [-со; оо ]; &[0;оо]; с[-1;1]; у (0;2] — параметры устойчивого закона, причем

G^ =

-tg^y/2); у ^ 1, (2 / л)/и|[/|; у = 1.

В четырех частных случаях соответствующие (1) варианты И'^х) могут быть записаны в аналитическом виде через элементарные и специальные функции (ограничимся а = с = 0 и для простоты опустим нормирующие множители в области ^[ХрХо]):

• -    модель I на основе нормального закона (у = 2), показанная на рисунке 3, г:

^(х) = (1 / 2Тл^)ехр(-л-² / 4Ь\      (2)

где максимум ПРВ соответствует ИДО) = (1 / /2^/^);

— модель II на основе закона Коши (у = 1):

ИДт) = 6/л[х2 +Z)2],          (3)

где максимум ПРВ есть ^(0) = (1 / лЬ);

• -    модель III при у = 1 / 2:

^ (х) = (1 / ^2л|х|³) Ф(/>² / 41 эф, (4) где максимум ПРВ равняется ИДО) = 2/ л/>², Ф(Ь² /4|х|) = cos(b² /4|т|) [0,5 - С(Ь² /4|х|)] +

+ sin(^² /4|х|) [0,5 - S(b² /4|х|)],

С(х) = ^2/л J cos(t)dt; о

S(x) = ^ 2/ л j sin(r)(7/ о

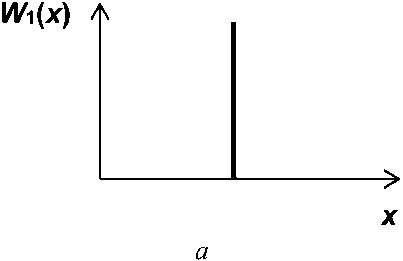
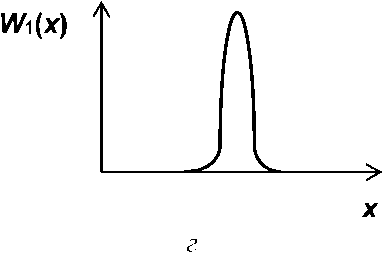
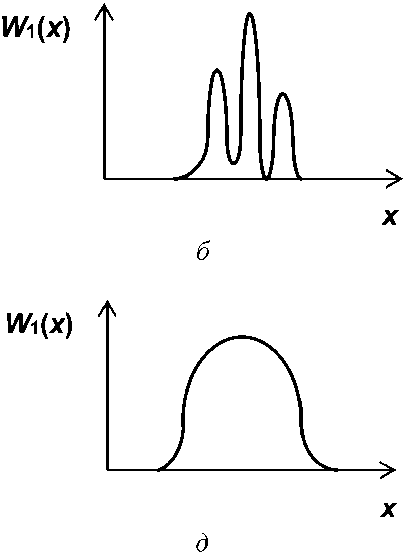
Рисунок 3. Типовые варианты реализации вероятностной модели хаотического процесса

• -    косинус-интеграл и синус-интеграл Френеля соответственно;

• -    модель IV при у = 2/3:

W_A О) = (1 / 2^37|л:|) ехр(2 Ъ³ / Пх" ) х х^__{1/2 1/6}(4£³ /27.x²),             ^<5)

где максимум ПРВ Л] (0) = (3 / 4^Z?³); W _х , (х) -функция Уиттекера.

В более общем случае семейство устойчивых законов является частью класса L П. Леви, а в еще более общем виде - принадлежит обширному классу безгранично делимых законов [8; 18]. Наибольшее применение из всех этих ПРВ получил, как известно, нормальный закон (см. рисунок 3, г), который: во-первых, соответствует условиям применимости ЦПТ ТВ; во-вторых, имеет конечные числовые параметры (среднее значение и дисперсию) в бесконечных пределах х[-оо;оо], что с учетом применения стандартных численных методов для реализации финитных моделей не представляется сегодня его особым достоинством.

При у > 2 ПРВ, соответствующая (2), перестает быть функцией, положительно определенной в бесконечных пределах, что недопустимо в рамках ТВ. Однако, поскольку данная модель находит применение в задачах, связанных с преобразованием и аппроксимацией распределений х в области значений, ограниченной условием Л](х)>0, такого рода финитные модели в [18] было предложено именовать формально устойчивыми распределениями. Они располагаются между равномерным и нормальным законами (см. рисунок 3, д), отличаясь от последнего более плоской вершиной и отрицательным значением коэффициента эксцесса. Современные пакеты прикладных программ реализуют модели ^(х), соответствующие (1), которые удовлетворяют условиям решения абсолютного большинства конкретных задач.

Способы управления хаотическим процессом

В свете изложенного представляется, что для моделирования неуправляемого хаоса (см. рисунок 2) могут быть использованы все вероятностные модели, приведенные на рисунке 3. Однако для моделирования управляемого хаотического процесса наиболее подходит композиционная модель, показанная на рисунке 3, б.

Во-первых, потому, что она соответствует схеме на рисунке 2, б.

Во-вторых, так как именно с нее начинается переход от упорядоченного хода событий в СС к беспорядочному, что является одним из признаков хаотичности наблюдаемого процесса.

В-третьих, можно предположить, что выполнение условий применимости ЦПТ ТВ означает переход к своего рода «самоуправлению» СС независимо от воли ЛПР по объективным законам ее функционирования, что противоречит аксиоме управляемости объекта для моделей на рисунках 3, в и г.

Пусть модель хаотического процесса имеет обобщенный вид

Xn, (6)

И = 1

где хп — модели факторов, как стохастических, так и детерминированных, которые влияют на состояние и поведение объекта моделирования, ц[1;7У]. Если «рычагами» управления являются среднее значение inAX^^mAx^        (7)

п = \ и дисперсия хаотического процесса

D^J^D^^ Rnm>К}D{xm}, (8) n=1             n

Для нормальной модели (см. рисунок 3, г) в общем случае m_v (лу} = о„; D^x„} = о;, и тогда

.V                N N