Вероятностные характеристики основных компонентов короны спокойного Солнца и расчет экваториального распределения яркости в диапазоне длин волн 1-100 см

Наблюдения профиля интенсивности центр–лимб спокойного Солнца на волнах сантиметрового и дециметрового диапазонов длин волн всегда вызывали интерес исследователей, так как это распределение отражает структуру верхней хромосферы, переходной зоны и нижней короны. Этой задаче посвящено достаточно много экспериментальных работ, обзор которых приведен в [Shibasaki et al., 2011]. Характерная форма радиального распределения яркости T b – почти неизменный уровень на большей части диска и резкое повышение его на лимбе – до сих пор не получила строгого объяснения.

Расчеты радиального распределения яркости по сферически симметричным моделям атмосферы показывают значительное несовпадение с данными наблюдений (см. например, [Simon, Zirin, 1969; Lantos, Kundu, 1972; Fürst et al., 1974, 1979; Serio et al., 1981]). В работе [Lantos, Kundu, 1972] было предложено распределение спикул по высоте, при котором расчет экваториального распределения яркости на волне 3.5 мм согласуется с наблюдательными данными. Однако применение этого подхода на длинах волн 1.2–11 см не дало хорошего согласия с наблюдательными данными даже по величине радиорадиуса [Fűrst et al., 1979].

Очевидно, что в расчетах радиального распределения яркости необходимо учитывать случайный характер присутствия не только спикул, но и петельных структур, а также свободного вещества. Однако в настоящее время нет наблюдательных данных о частотах появления петель и спикул, нет статистики их размеров, высотных профилей плотности и температуры электронов. Более того, нет надежды, что такие данные вообще могут быть получены. Есть большое число публикаций по наблюдениям петель в рентгеновском и УФ-диапазонах, по петлям переходной области и даже неразрешаемым петельным структурам, а также по теории нагрева петель (см, например, [Serio et al., 1981; Oluseyi et al., 1999; Peres, 2000; Aschwanden et al., 2001]). Но при этом теоретические модели петель далеко не всегда согласуются с данными наблюдений, и, кроме того, их трудно использовать в расчетах. Тем не менее, используя вероятностный подход к оценке яркости и подбирая характеристики компонентов короны, можно получить удовлетворительное согласие теоретических и наблюдательных данных по экваториальному распределению яркости. Если такого согласия удастся достигнуть в широком диапазоне длин волн, можно будет утверждать, что найдена вероятностная структура атмосферы спокойных участков Солнца. Этой задаче и посвящена данная работа.

Вероятностная структура и метод расчета яркости не могут быть универсальными, т. е. применимыми к любой частоте излучения, в силу глубокого различия физических условий распространения излучения. В настоящей работе рассматриваются особенности излучения из области, охватывающей верхнюю хромосферу, переходную зону и нижнюю часть короны спокойных участков Солнца.

Ниже описывается принцип расчета яркости неоднородной атмосферы и приводятся результаты моделирования вероятностной структуры атмосферы и расчета экваториального распределения яркости в диапазоне от 1 до 100 см.

Методика моделирования. Принципы расчета экваториального распределения яркости

Для расчета яркости спокойных участков используется представление случайного набора петельных структур совокупностью ранжированных по размерам петель, у которых частота появления αr и величина плотности электронов на вершине являются средними для петель данной области размеров. Аналогичным образом в расчете учитывается присутствие спикул – быстро изменяющихся структур в солнечной хромосфере, наблюдаемых на лимбе. Распределение спикул на диске неравномерно, большинство из них расположено на границах супергранул. Примем, тем не менее, что для нашей задачи распределение спикул по диску можно считать равномерным.

Яркость однородной атмосферы на высоте h , как известно, определяется выражениями

T = J Т (h )exp(-T( h)) dt,(1)

t( h) = jd t,(2)

где, согласно [Pineau des Forêts, 1979], dt = 0.0122/ f2n2 x e ,(3)

x(T-3/2 (17.72 + 1g(T3/2 / f)dh / np, np = (1 — (f,1/ f )T.(4)

Здесь T ( h ), n e ( h ), n p ( h ) – высотные профили температуры, плотности электронов и коэффициента преломления соответственно, f – частота излучения, f _pl – плазменная частота. Если излучение участка атмосферы наблюдается под углом к градиенту плотности электронов, то под dh в этом случае подразумевается длина пути в слое, а при определении коэффициента преломления надо учитывать, что отражение падающей волны происходит, когда cos²θ = ( f pl / f )² [Железняков, 1964].

Яркость неоднородной атмосферы можно найти, если известны яркости и вероятностные характеристики участков петель и спикул по какой-то сетке высот. Пусть на данной высоте существует в среднем n петель и m спикул. Разобьем по высоте эти детали на участки, толщина которых определяется средней длиной пробега луча в петле или спикуле, а затем сформируем из последовательностей таких участков общую сетку высот h s . Тогда яркость короны T b ( i ) на высоте h s ( i ) определится выражением

T b ( i ) = T _b ( i - 1) + n ( i - 1) x

( n

XI E Tb1p(i’ j)Pv1( 1, j)B1s ( 1, j)eXP(-T1p(i, j) + к j=0

m

+ E Tbsp (i, k)Pvsp(P, k)B1s (P, k)eXP(-Tsp(i, k)) ) + k=0

+ T b _S v ( i ) N b1s ( i )exp( -T _S v _O ( i )).                         (5)

Здесь η(i) – коэффициент передачи, Tblp(i, j), τblp и Tbsp(i, k), τbsp – яркости и затухание соответственно j-й петли и k-й спикулы между высотами hs(i–1) и hs(i), τsvo(i) – затухание в свободном веществе до данной высоты, Pvl(l, j) – вероятность встречи l-го участка j-й петли, толщина Ahgr(l, j) которого соответствует средней длине пробега в петле в окрестности i-го слоя, Pvsp(p, k) – вероятность встречи p-го участка k-й спикулы, толщина Ah@(p, k) которого соответствует средней длине пробега в спикуле в окрестности i-го слоя, Bls(l, j) и Bls(p, k) – вероятность отсут- ствия других петель и спикул на интервале соответственно Ahgr(l, j) и Ahgr(p, k), Nbls(i) - вероятность отсутствия петель и спикул на данной высоте. Коэффициент передачи равен

П(i) = П(i-1) I E Pv1(1, j1)B1s(1, j1)x к j1 =0

^{x e} xp ^{( -T} 1p⁽ i , JO +

+ E Pvsp( P, k1) B1s ( P, k1) x k1 =0

^{x e} xp ^{( -T} sp ⁽ i , ^k 1 )) ) ⁺ N b1s ⁽ i ) ^e xp ^{( -T} svo ⁽ i )),

где j 1 и k 1 – петли и спикулы, у которых нижняя граница A h gr совпадает с высотой h _s( i ).

Используя изложенный принцип, можно провести расчет яркости атмосферы, если задаваться параметрами компонентов короны. Для сужения области поиска этих параметров в работе используется ряд допущений.

Определение высотных профилей температуры и плотности петель и свободного вещества тесно связано с исходными профилями атмосферы T ( h ) и n e ( h ), удовлетворяющими наблюдательным данным о яркости в центре диска Солнца. В данной работе за основу взята модель спокойной атмосферы для центра диска (высотные профили), полученная путем соединения корональной части модели, описанной в [Гетман, Лившиц, 1996], и комбинации моделей FALA и FALF хромосферы и переходной области [Fontenla et al., 1993] в соотношении FALA·0.965+FALF·0.035. Эти высотные профили плотности и температуры назовем исходной моделью.

Всю совокупность петель короны можно представить в виде набора кластеров близких по размеру петель и в расчетах использовать параметры средних (по размерам) петель этих кластеров. В работе принят набор из десяти таких петель с размерами, пропорциональными среднему размеру хромосферной сетки, т. е. с радиусами R _loop от 15 000 до 210 000 км, а также c существенно меньшими размерами ( R _loop=7200, 3100 км).

Принято также, что толщина петель неизменна по всей длине [Klimchuk, 2000] и равна R _loop/15, сами петли ориентированы по радиусу Солнца, а положение их относительно луча зрения равновероятно в интервале 0-2 п . Частота появления петель определяется как число петель данного размера, находящихся на площадке 2 R _loop x 2 R loop .

Высота начала корональной части петель h ₀=2275 км, принятая в работе, соответствует максимальной высоте модели FALA. Для высотного профиля температуры корональной части петель использовано выражение

×

T lp ( h ) =T min + ( T max loop – T min )

× (sin(π/2( h–h 0 )/( R loop –h 0 ))) a lp , (7) где T _min – температура исходной модели на высоте h ₀, T _{max loop} – температура вершины петли, a _lp – подбираемый параметр, определяющий степень «пря-моугольности» профиля.

Плотность электронов петли находится по выражению nelp(h)=p0exp(–(h–h0)/λp0)/(2kbolzTlp(h)), (8) где p0 – давление на высоте h0, kbolz – постоянная Больцмана, λp0=(Rloop)/lg(p0/p1) – масштаб высоты по давлению, p1 – давление в вершине петли, подбираемое, как и p0, при моделировании.

Априори можно считать, что в короне основной вклад в излучение дают петли, поэтому T _{max loop} должна быть примерно той же величины, что и температура исходной модели. В работе T max loop равна температуре в исходной модели на соответствующей высоте, а плотность в поперечном сечении имеет небольшой спад (5 %) к внешней оболочке.

Для области ножек петель принято, что высотный профиль температуры совпадает с профилем температуры в исходной модели, а профиль плотности определяется по исходному профилю n _e( h ) в этой области:

nelp(h)=ne(h)p0/psh, где psh – давление исходной модели на высоте h0.

Для спикул за основу взята их стратификация (относительная площадь диска z sp , покрытая спикулами, достигающими определенной высоты), предложенная в [Lantos, Kundu, 1972]. В ходе моделирования эта стратификация дополнена более подробным ранжированием спикул по размерам и вероятностям нахождения на определенных высотах. Для упрощения расчетов спикулы представлены как небольшие вырезки из кольцевой формы, радиус которой подобран с таким расчетом, чтобы средний угол наклона спикулы был равен 22º. Плотность спикул снижается от оси к внешней оболочке на 40 %.

Если выбраны параметры петель и спикул, можно приближенно определить параметры свободного вещества, исходя из следующих соображений. В короне высотный профиль температуры свободного вещества не может существенно отличаться от профиля в исходной модели, так как это вещество должно формироваться преимущественно из материала распадающихся петель. Как показано в [Боровик и др., 1990], температура атмосферы корональ-ных дыр, где мало петельных структур, ниже температуры спокойных областей примерно на 20 %, поэтому высотный профиль температуры свободного вещества принят равным профилю в исходной модели.

Профиль плотности свободного вещества nesv(h) корректно определить нельзя. Однако, учитывая, что в корональной области основная часть вещества заключена в петельных структурах, а в хромосфере – в свободном веществе (это предположение условно для рассматриваемого диапазона волн), можно оценить nesv(h) по приближенному соотношению для интервала высот Δh(i)

n esv ( i ) ≈ n e ( i ) –D lp ( i ) –D sp ( i ), (9) где n _e( i ) – средняя плотность исходной модели в слое Δ h ( i ), D _lp( i ) и D _sp( i ) – соответственно совокупные плотности петель и спикул в этом слое с учетом их частот появления температур.

Для упрощения расчетов предварительно все петли разбиваются по высоте на отдельные участки, верхний из которых представляет собой вершину петли. Остальные участки организуются так, чтобы горизонтальные проекции верхнего и нижнего сечений примыкали друг к другу. Далее производится расчет вероятности попадания луча в эти участки P _vk( i , j ), для чего определяются проекции участков на горизонтальную плоскость в четырех ортогональных пространственных положениях петель (продольные по лучу зрения и поперечные положения). Используя закон Пуассона, находим

P vk ( i , j ) = 1 – exp(– Nl·dP u ·dlP u ), (10) где N _l – число ножек петли на единицу площади, dP u , dlP u – средние значения проекций участков по лучу зрения и в перпендикулярном направлении.

Проекции не должны захватывать высоты ниже h min – высоты отражения луча в свободном веществе или высоты, на которой затухание превышает величину 10 дБ. Поэтому предварительно производится соответствующий расчет затухания при прохождении свободного вещества, а также высотных зависимостей угла падения α sv и коэффициента преломления n _psv.

В этой же части расчетов определяется средняя величина пробега луча в каждом участке петли, что позволяет далее найти Δ h gr ( l , j ) и вероятности P _vl( l , j ) попадания луча в такой слой петли. Аналогичным образом находятся вероятности P _vsp( m , k ) для спикул.

Из полученных последовательностей Δ h _gr( l , j ), P hgr ( m , k ) для петель и спикул формируется сетка высот h s , по которой далее производятся расчеты яркостей.

Вероятности отсутствия других деталей спокойных участков B ls ( l , j ) и B ls ( m , k ) определяются для каждого интервала dh _gr петли (или спикулы) и представляют собой произведение вероятностей отсутствия других петель и спикул на этом интервале. Вероятность отсутствия петель и спикул N _bls( i ) находится на каждой высоте сетки h _s( i ) как произведение вероятностей отсутствия участков петель и спикул в окрестности высоты h s ( i ), равных ближайшему интервалу dh gr этих элементов.

Яркость свободного вещества вычисляется по найденным выше профилям температуры и плотности электронов, а также высотным зависимостям n psv и угла падения α sv .

Яркость слоя петли находится как среднее значение яркостей слоя при четырех возможных его положениях. При расчете яркости слоя в каждом положении определяется траектория луча внутри петли – угол падения относительно текущего градиента плотности и длина пробега в исходной системе координат. Если в слое происходит отражение луча, производится расчет яркости по траектории отраженного луча. Результирующее затухание в слое вычисляется по затуханиям составляющих с учетом их веса.

Аналогичным образом вычисляются яркости спикул.

Общая яркость спокойного участка атмосферы находится по описанному выше алгоритму. Если результирующее затухание в свободном веществе меньше 10 дБ, результирующая яркость

T b =T b0 (1+ η 0 ), (11) где T b0 , η 0 – яркость и коэффициент передачи на высоте h min .

В целом процесс итерационного моделирования заключается в следующем: задаются параметры петель ( p 0 , p 1 , α r , α lp ) , спикул (n esp0 , T sp , D sp , H spn , H spv , z sp ), определяется высотный профиль свободного вещества n _esv( h ). После этого на заданной длине волны производится расчет яркости атмосферы вдоль экватора к лимбу. По результатам сравнения результатов расчета с известными наблюдательными данными изменяются исходные параметры петель и спикул и расчеты повторяются.

Результаты моделирования и расчета экваториального распределения яркости

В табл. 1 приведены параметры петель, полученные в результате моделирования: коэффициент разреженности α r , плотность электронов в вершине петли n e max loop , температура вершины петли T max loop , давление в основании корональной части p ₀ и в вершине петли p 1 .

Для параметра a lp наилучшее согласование с наблюдательными данными получается при его значении, равном 0.25.

В табл. 2 приведены параметры спикул – высоты оснований H spn , вершин H spv , толщина D sp , плотность электронов n _esp0, температура T _sp и относительная площадь, занимаемая спикулами данного размера z _sp .

В табл. 3 приведены расчетные параметры экваториальных распределений яркости на длинах волн от 1 до 100 см, а также параметры, полученные при наблюдениях на радиотелескопах с высоким угловым разрешением. Здесь T b (0) – яркость в центре диска ( K ), k – радиальное расстояние от центра диска вдоль экватора в долях солнечного радиуса (на уровне фотосферы), k max – радиальное расстояние пика яркости, γ – уровень пика яркости относительно яркости в центре диска, R 0.5 – радиорадиус на уровне 0.5 величины T _b(0) (в долях солнечного радиуса), p – позиционный угол Солнца при наблюдениях.

Отличие расчетных величин яркости в центре диска от известных экспериментальных данных [Zi-rin et al., 1991; Боровик и др., 1992] в основном меньше 5 %. Для длины волны 1см в качестве экспериментального значения приведен результат вычисления по формуле аппроксимации наблюдательных данных миллиметрового диапазона [Loukitcheva et al., 2004]

T = 5777 - 978 lg λ + 3489(lg λ ) ² , (12) где λ – длина волны в мм.

На рисунке для примера приведены расчетные экваториальные распределения яркости на длинах волн 1.7 и 5.2 см. Здесь по оси абсцисс – расстояние от центра диска Солнца k в долях солнечного радиуса (на уровне фотосферы), по оси ординат – величины яркости T _b( k ), нормированные на значение яркости в центре диска T _b(0). Штрихпунктирной линией нанесены значения яркости свободной составляющей T bsv , нормированные также на T b (0).

На значительной части диска, особенно на коротких волнах, величина T bsv , во многом определяющая результирующую яркость, практически не изменяется. При удалении от центра диска увеличиваются угол падения и длина пути в свободном веществе до высоты h _min, ниже которой плазма не излучает в направлении данного угла падения. Величина h _min увеличивается с углом падения, что ограничивает длину пути в плотных слоях свободного вещества, следовательно, наряду с факторами депрессии B ls и N bls , и величину яркости свободного вещества. Резкое увеличение яркости на сантиметровых длинах волн наступает тогда, когда τ svo – оптическая толщина свободного вещества до h min – становится небольшой и вклад отраженного луча получается ощутимым.

В центральной части диска в распределении яркости обнаруживаются небольшие флуктуации, среднеквадратичное значение которых в основном не превышает 0.5 %. В области радиальных расстояний 0.5–0.8 на длинах волн 1–3.2 см существует спад яркости до 3 %. Анализ показал, что основная причина этого спада – отражения падающего луча от внешней оболочки ножек петель. На длинных волнах уровень флуктуаций увеличивается, особенно в области лимба, из-за внутренних отражений в петлях.

В центральной части диска, на радиальных расстояниях до 0.9, как следует из табл. 1, получено хорошее согласие с данными наблюдений на РАТАН-600 [Богод, 1996].

В диапазоне длин волн 8.2–31.6 см расчетные значения пика яркости, его углового положения и величины радиорадиуса также хорошо согласуются с экспериментальными данными, полученными другой группой исследователей на РАТАН [Borovik, 1994].

Наибольшее расхождение с результатами работы [Borovik, 1994] оказалось в области длин волн 2–4 см. Так, на длине волны 2 см расчетный относительный уровень пика яркости составляет 1.22, величина радиорадиуса 1.002, а по [Borovik, 1994] соответственно 1.02 и 1.026.

В этой связи рассмотрим данные измерений радиорадиуса Солнца на близкой волне 1.7 см по радиоизображениям, полученным на радиогелиографе Нобеяма (NoRH). В работе [Selhorst et al., 2004], посвященной измерениям радиорадиуса на волне 1.7 см вдоль всего лимба по данным NoRH, показано, что средний радиус варьирует от 976.6 ± 1.5 до

Таблица 1

Параметры петель

R loop, 10 , км	210	180	150	120	90	60	30	14.7	7.2	3.1
a r	8.7	6.1	8.1	8.2	8.1	8.6	8.6	6.6	7.8	6.8
n e max loop , 10 см	3.03	3.57	4.15	4.74	5.37	6.35	6.91	7.49	8.6	9.23
T max loop, 103 K	1540	1540	1540	1539	1528	1519	1499	1460	1345	1320
p 0, 10–8 дин см–2	2.16	2.26	2.35	2.47	2.57	2.75	2.83	2.95	3.08	3.22
p 0 /p 1	1.85	1.63	1.47	1.35	1.25	1.13	1.087	1.07	1.06	1.05

Таблица 2

Параметры спикул

H spv, км	11000	8000	6000	3200	2550	1960	1600	1000	700	400
H spn,км	3650	2550	1960	1960	1600	686	560	350	245	0
D sp ,км	1320	1200	1122	392	298	544	375	360	240	180
Z sp , 10–2	0.156	0.144	0.3	0.216	0.484	2.516	1.484	1.0	1.0	1.0
n esp0 , 109 см–3	60	60	60	70	80	90	100	160	160	160
T sp , 103 K	20	20	20	20	20	20	20	20	20	20

Таблица 3

Параметры экваториальных распределений яркости

X , см	T b (0), K	k =0.5	k =0.7	k =0.9	k max	Y	R 0.5	Примечание
1	8000	1.0	<1.0	1.0	1.0015	1.124	1.003	Расчет
	8288							Эксп., по [Loukitcheva et al., 2004]
1.7	9400	<1.0	<1.0	1.005	1.001	1.2	1.003	Расчет
	10000							Owens Valey, [Zirin et al., 1991]
						1.12		NoRH, [Selhorst et al., 2004]
2.0	9870	<1.0	<1.0	1.015	0.998	1.22	1.003	Расчет
	10700							Owens Valey, [Zirin et al., 1991]
	10400							РАТАН-600, [Боровик и др., 1992]
		1.0	1.0	1.03				РАТАН-600, [Богод и др., 1996]
					1.0	<1.02	1.026	РАТАН-600, [Borovik, 1994] p =26 °
2.3	10380	<1.0	<1.0	1.025	0.998	1.248	1.003	Расчет
	10800							Owens Valey, [Zirin et al., 1991]
	10900							РАТАН-600, [Боровик и др., 1992]
					1.0	1.03±2	1.03	РАТАН-600, [Borovik, 1994] p =26 °
2.7	11060	<1.0	<1.0	1.043	0.998	1.296	1.004	Расчет
	11100							Owens Valey, [Zirin et al., 1991]
	11500							РАТАН-600, [Боровик и др., 1992]
					1.0	1.05±2	1.035	РАТАН-600, [Borovik, 1994] p =26 °
3.2	11900	<1.0	<1.0	1.054	0.996	1.315	1.005	Расчет
	12200							Owens Valey, [Zirin et al., 1991]
	12400							РАТАН-600, [Боровик и др., 1992]
		1.0	1.0	1.04				РАТАН-600, [Богод и др., 1996]
					1.0	1.1±2	1.041	РАТАН-600, [Borovik, 1994] p =26 °
4.0	13360	<1.0	1.0	1.077	0.993	1.33	1.01	Расчет
	13400							Owens Valey, [Zirin et al., 1991]
	13200							РАТАН-600, [Боровик и др., 1992]
		1.0	1.0	1.05				РАТАН-600, [Богод и др., 1996]
					1.0	1.15±2	1.052	РАТАН-600, [Borovik, 1994] p =26 °
5.2	15720	1.0	1.03	1.129	0.988	1.36	1.052	Расчет
	16000							Owens Valey, [Zirin et al., 1991]
							1.05	ССРТ, [Лубышев и др., 1999]
					0.99	1.37	1.06	ССРТ, [Криссинель, 2005]
6.0	17210	1.01	1.05	1.151	0.984	1.45	1.078	Расчет
	17600							Owens Valey, [Zirin et al., 1991]
8.2	21880	1.04	1.093	1.238	0.99	1.72	1.121	Расчет
	21700							Owens Valey, [Zirin et al., 1991]
	21100							РАТАН-600, [Боровик и др., 1992]

		1.01	1.03	1.19				РАТАН-600, [Богод и др., 1996]
					0.98	1.34±5	1.095	РАТАН-600, [Borovik, 1994] p =26 °
11.7	30870	1.06	1.149	1.365	0.985	2.22	1.178	Расчет
	30500							Owens Valey, [Zirin et al., 1991]
	29600							РАТАН-600, [Боровик и др., 1992]
		1.04	1.12	1.43				РАТАН-600, [Богод и др., 1996]
					0.98	1.95	1.135	РАТАН-600, [Borovik, 1994]
20.7	65200	1.1	1.23	2.13	0.995	2.64	1.205	Расчет
	67000							Owens Valey, [Zirin et al., 1991]
	59600							РАТАН-600, [Боровик и др., 1992]
		1.11	1.22	2.22				РАТАН-600, [Богод и др., 1996]
					0.95	3.0	1.188	РАТАН-600, [Borovik, 1994]
31.6	127940	1.18	1.62	2.31	1.0	3.14	1.23	Расчет
	131000							РАТАН-600, [Боровик и др., 1992]
		1.11	1.55	2.61				РАТАН-600, [Богод и др., 1996]
					0.93	2.48	1.205	РАТАН-600, [Borovik, 1994]
100	1063800	1.11	1.48	2.047	0.98	2.1	1.161	Расчет

974.8 ± 0.6 угл. сек. Если учтем среднюю величину оптического радиуса (961.34 угл. сек), то отличие радиорадиуса от оптического составит около 15 " . В работе [Nindos et al., 1999] сообщается, что на картах NoRH радиорадиус равен 1.0125, т. е. те же 15 " за оптическим лимбом. По нашим расчетам величина радиорадиуса равна 1.003. Если свернуть расчетное распределение с диаграммой направленности NoRH (15x15 " ), то, как видно из рисунка (штриховая линия, верхняя панель), радиорадиус увеличится до 1.007. Здесь следует отметить, что измерения радиорадиуса по картам NoRH содержат ряд погрешностей, таких как точность центровки, обусловленная размером пикселя изображения (4 " ), ошибки наведения антенн, калибровки яркости, погрешности восстановления яркости процедурой «чистки»; необходимо учитывать также влияние яркости корональных точек. Ширина теоретического отклика на уровне 0.5 меньше наблюдаемого примерно на 5 " , что с учетом указанных погрешностей измерений, а также погрешностей расчета можно считать хорошим согласием. Расчетная величина пика равна 1.2, но при учете влияния диаграммы направленности (ДН) снижается до величины 1.1 и фактически совпадает с наблюдательными данными [Nindos et al., 1999].

Причина расхождений с данными [Borovik, 1994], на наш взгляд, заключается в наблюдательных ограничениях и методике восстановления распределения яркости. В области коротких волн разность расчетного радиорадиуса и оптического в несколько раз меньше ширины ДН радиотелескопа РАТАН-600 (на 2 см - 17 " x15) что делает проблематичной возможность точного восстановления профиля лимба. Для длинноволновой части диапазона такого противоречия нет, и расчетные данные хорошо согласуются с данными [Borovik, 1994].

На волне 5.2 см расчетные величины пика и радиорадиуса хорошо согласуются с данными наблюдений на Сибирском солнечном радиотелескопе (ССРТ) [Grechnev et al . , 2003], полученными при наблюдении затмения [Лубышев и др., 1999], а также путем обработки большого числа наблюдений на одномерных решетках [Криссинель, 2005]. Если свернуть теоретическое распределение яркости с ДН

ССРТ (23x23 " ), то, как показано на рисунке (штриховая линия, нижняя панель), пик яркости снижается с 1.36 до 1.27, но радиорадиус при этом не увеличивается.

На длине волны λ=6 см известны наблюдательные данные, полученные на синтезированных радиотелескопах WSRT [Kundu et al., 1979] и VLA (совместно с ORPWO) [Marsh et al., 1981]. Как следует из работы [Kundu et al., 1979], пик температуры лимба ~ на 40 % больше температуры диска, но при этом пик смещен на 15 " за лимб, а радиорадиус превышает оптический на 40 " , что не согласуется по этим параметрам для других длин волн и характеризует трудности интерпретации данных синтезированных радиотелескопов. Это же относится и к работе [Marsh et al., 1981] по наблюдениям во время частичного солнечного затмения: на λ=6 см получена величина лим-бового уярчения (80 %), значительно превышающая данные других исследователей, а на λ=2.8 см наблюдалось лишь небольшое возрастание яркости.

Расчетные экваториальные распределения достаточно устойчивы при изменении вероятностных характеристик компонентов модели в пределах ±10 %: изменяются немного лишь значения яркости в центре диска и радиорадиуса.

Предложенная модель спокойных участков Солнца имеет ограничения по частотам излучения. На длинах волн, превышающих 1 м, теоретические экваториальные распределения показывают сильную неравномерность вследствие большого числа внутренних отражений в петлях, что вызвано идеализацией формы петли, принятой в работе. Петли больших размеров, как известно, представляют собой скрутку большого числа тонких петель, и траектория луча в такой петле не может быть идентичной траектории в петле из одной нити. Кроме того, на длинных волнах необходимо уже учитывать эффекты рассеяния на корональных неоднородностях [Aubier et al., 1971], что выходит за пределы поставленной задачи.

Теоретические распределения на миллиметровых волнах по предложенному алгоритму имеют существенный тренд по диску и большой пик на лимбе, что не соответствует данным наблюдений. Это объясняется тем, что на этих длинах волн вплоть до лимба излучение идет из хромосферы, а в предложенную

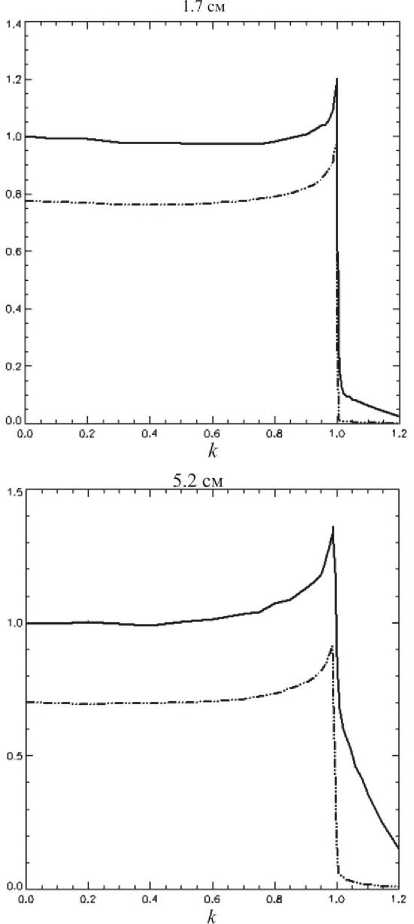
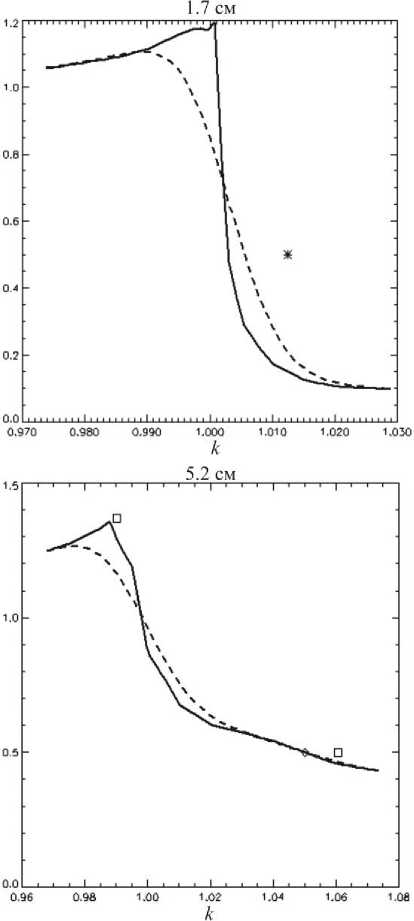
Расчетные экваториальные распределения яркости на длинах волн 1.7 ( а ) и 5.2 см ( б ). По оси абсцисс – расстояние от центра диска Солнца k в долях солнечного радиуса (на уровне фотосферы), по оси ординат – величины яркости T _b( k ), нормированные на значение яркости в центре диска T _b(0). Штрихпунктирной линией нанесены значения яркости свободной составляющей T _bsv, нормированные также на T _b(0). Штриховая линия – свертка расчетного распределения с ДН радиотелескопа (ширина ДН NoRH (1.7 см) составляет 15×15 " , ССРТ (5.2 см) – 23×23 " ). Метки – экспериментальные данные: ∗ – [Selhorst et al., 2004], □ – [Криссинель, 2005], ◊ – [Лубышев и др., 1999].

структуру спокойных участков не включены характеристики основных деталей хромосферы, таких как малоразмерные петли и яркие точки, ввиду отсутствия в литературе каких-либо сведений о них. Находить же моделированием вероятностные характеристики деталей хромосферы в настоящее время невозможно из-за отсутствия экспериментальных распределений яркости на волнах миллиметрового и субмиллиметрового диапазонов. Поэтому предложенная модель структуры спокойных участков Солнца может объяснять излучение только от высот выше 1000 км.

Обращаясь к графикам распределений яркости, отметим, что вопреки ожиданиям в коротковолновой части уровень яркости не равен нулю на значительных расстояниях от лимба. Это необходимо учитывать при обработке данных солнечных наблюдений, когда при калибровке используют уровень «неба».

Заключение

В настоящей работе предложена модель атмосферы спокойных участков Солнца, компоненты которой описываются вероятностными характеристиками. Эта модель, охватывающая переходную зону и нижнюю корону, представлена совокупностью ранжированных по размерам петель, спикул и свободного вещества. Для расчета яркости многокомпонентной атмосферы разработан алгоритм, использующий вероятности появления компонентов в каждом слое атмосферы, средние значения их яркости и коэффициент передачи, определяемый также с учетом вероятностных характеристик. Характеристики компонентов модели определялись моделированием путем сравнения параметров расчетных и экспериментальных экваториальных распределений яркости. В результате параметры теоретического экваториального распределения яркости многокомпонентной атмосферы впервые оказались в хорошем согласии с известными наблюдательными данными в широком диапазоне длин волн.

При разработке модели был сделан ряд допущений при нахождении параметров свободного вещества, высотных профилей петель и спикул. Эти допущения позволили упростить задачу, но в то же время явились одной из причин ограничения применимости модели на длинах волн короче 1 см, так как в настоящее время отсутствуют необходимые данные о компонентах хромосферы и экспериментальные распределения яркости на волнах миллиметрового и субмиллиметрового диапазонов.

Представляется, что описанный подход к построению модели спокойных участков может быть применен при исследовании атмосферы спокойного Солнца на всех широтах, а также корональных дыр.

Измерение вариаций солнечного радиуса на радиочастотах представляет, по мнению ряда исследователей (см., например, [Selhorst et al., 2004]), глобальный индикатор изменений солнечной атмосферы, в связи с чем результаты данной работы могут быть использованы в этом направлении как отправная точка измерений при отсутствии активностей.

Автор признателен коллективу отдела радиоастрономии ИСЗФ СО РАН за полезное обсуждение работы.

Работа проводилась при финансовой поддержке Министерства образования и науки Российской Федерации.