Вероятностные модели исследования процессов подготовки аналитических материалов

Основными функциональными задачами ежедневно многократно решаемыми аналитиками в интересах органов государственной власти в информационно-аналитических центрах (ИАЦ), построенных на основе локальных вычислительных сетей (ЛВС), при подготовке информационноаналитических материалов (ИАМ) являются поиск информации по фактографии, поиск информации по содержанию (контекстный) частотный анализ по атрибутам документов, сортировка документов, кластеризация отобранных документов, семантический анализ.

Необходимым условием сокращения сроков разработки и повышения качества функционирования, распределенных информационновычислительных систем является разработка методов анализа эффективности реализуемых информационных технологий, в первую очередь типовых технологий подготовки аналитиками информационноаналитических документов [1, 2, 3, 4, 5, 6]. Разработка математических моделей, описывающих основные этапы и схемы подготовки ИАМ позволяет на основе многовариантного анализа различных технологий подготовки ИАМ автоматизировать выбор технических, программных и информационных компонент ЛВС, с помощью которых осуществляются различные режимы работы аналитиков при подготовке ИАМ. Основными методами исследования процессов подготовки ИАМ являются методы теории вероятностей [7], теории случайных процессов [8, 9], теории надежности и массового обслуживания [10, 11, 12, 13, 14, 15, 16].

Функциональные уравнения сетевых вероятностных моделей исследования процессов подготовки ИАМ

Основные технологические процессы подготовки ИАМ формализованы в виде 4 классов сетевых вероятностных моделей описывающих - технологические операции, выполняемые аналитиками функциональные задачи, решаемые в клиент-серверном режиме аппаратно-программными средствами ИАЦ, а также последовательность выполнения технологических операций и решения функциональных задач. При этом узлы сети соответствуют технологическим операциям и функциональным задачам, а дуги соответствуют вероятности перехода от одного узла сети к другому. Время выполнения операции в узле сети является случайной величиной и описывается функцией распределения (ФР) этой случайной величины. Параметры ФР времени выполнения технологических операций аналитиками (1-ый и 2-ой моменты ФР) определяются методами математической статистики на основании измерений [8, 9].

Параметры ФР времени решения функциональных задач на серверах ИАЦ (моменты ФР) рассчитываются с помощью вложенной модели оценки временных характеристик обработки информации на аппаратнопрограммном уровне [10, 15].

Функциональные уравнения сетевых вероятностных моделей исследования процессов подготовки ИАМ базируются на использовании свойств аппарата преобразований Лапласа-Стильтьеса [1, 2, 14] заключающихся в том, что:

• -    преобразование Лапласа-Стильтьеса функции распределения некоторой случайной величины является производящей функцией для моментов ФР этой случайной величины;

• -    преобразование Лапласа-Стильтьеса ФР случайной величины являющейся суммой независимых случайных величин, является произведением преобразований Лапласа-Стильтьеса ФР этих случайных величин.

В частности, эффективность применения математического аппарата базирующегося на свойствах преобразований Лапласа-Стильтьеса ФР случайных величин, была продемонстрирована при разработке аналитических моделей исследования процессов обработки информации в локальных вычислительных сетях [16].

Рассмотрим простейший технологический процесс подготовки ИАМ. При поступлении запроса на подготовку ИАМ выполняются следующие действия:

• -    с вероятностью P i готовится предписание на фактографический поиск (ФР П() ), выполняется поиск (ФР T i (t) ), анализируются отобранные документы (ФР a i (t) ), с вероятностью P_n уточняется предписание П 1 и повторяется операция поиска T i , а с вероятностью P 12 (P i2 =1-P ii ) результаты передаются на конечную операцию – анализ выходной коллекции документов A 4 (ФР A() );

• -    с вероятностью P 2 готовится предписание на контекстный поиск (ФР n 2 (t) ), выполняется поиск (ФР T 2 (t) ), анализируются отобранные документы (ФР a 2 (t) ), с вероятностью P 21 у точняется предписание П 2 и повторяется операция контекстного поиска T 2 , а с вероятностью P 22 (P 22 =1-P 21 ) результаты передаются на конечную операцию - анализ выходной коллекции документов A 4 (ФР A 4 (t) ).

Функциональное уравнение, описывающее преобразования Лапласа-Стильтьеса функции распределения времени подготовки ИАМ X * (s) Оф’"^)/   ___

• -      , имеет вид:

X*(s) = Pi{(1-Pn)ni*(s)Ti*(s)ai*(s)A4*(s)/[1-Piini*(s)Ti*(s)ai*(s)]} + +P2{(i-P!i)n!ys)T7s)a!ys)A4\s)/[i-P2^

n*(s) = f e^dn, (?) rr(s) = j e^’dT,(t) a*(s) = f e-'da,(t)

где                  ,               ,, n2*(s) = Je~5,dn2(t) T2*(s) = Je^'dT2(p a2*(s) = je~'’da2 (t) о                             о0

Действительно функциональное соотношение, описывающее фактографический поиск имеет вид:

f^^pF^-pM^t;^^ = ^^[^wWc»))* = 4=1                                                          *11    4=1

₌ о-^ЖЖЖ^ = a-p ) ^WiWlv)

^Ж’ЖЖ где                  - преобразование Лапласа-Стильтьеса функции распределения времени выполнения операции фактографического поиска документов (Fфп (t)).

Дифференцируя соотношение (2) по s и полагая s=0, можно легко получить следующую формулу для оценки среднего времени операций фактографического поиска:

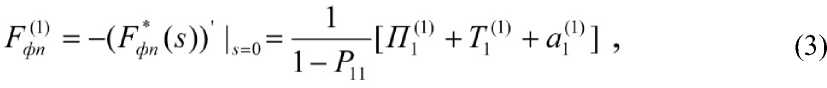
П ^{( 1})

где ^{П 1}   - среднее время подготовки оператором предписания на

(i)

фактографический поиск на рабочей станции, ^{T 1} - среднее время выполнения фактографического поиска на сервере ЛВС по заданному (¹)

предписанию, a 1 - среднее время анализа на рабочей станции аналитиком документов, отобранных при фактографическом поиске по заданному предписанию, и принятие решения о корректировке операции поиска.

(i)         (i)

Оценка параметров ^{П 1} , ^{a 1} , а также вероятности P 11 осуществляется статистическими методами на основе непосредственных измерений операций, выполняемых аналитиками на рабочих местах ЛВС.

Функциональные соотношения, описывающие операции контекстного поиска, имеют вид:

M                                   [1-P2]P2№2 (5>2(i)]         v 7

к«=р-ж«     _        „    „        , где               - преобразование Лапласа-Стильтьеса функции распределения (Fkn (t)) времени выполнения операций контекстного поиска документов в ЛВС, включая операции на рабочей станции и сервере поиска.

Из выражения (4) легко получить следующую формулу для оценки среднего времени операций контекстного поиска в ЛВС:

где П 2  - среднее время подготовки оператором предписания на контекстный поиск на рабочей станции, T2 - среднее время выполнения фактографического поиска на сервере ЛВС по заданному предписанию

• ^{a 2} - среднее время анализа на рабочей станции аналитиком документов отобранных при контекстном поиске по заданному предписанию, и

• принятия решения о корректировке предписания на поиск.

Определив с помощью вложенной модели аппаратно-программного уровня параметры ФР Ti(t) и T2(t) [3, 10, 15] и дифференцируя функциональное уравнение (1) по s, легко получить расчетные соотношения для оценки среднего значения ( Х1 ), дисперсии подготовки ИАМ (X(t)) для заданного частности, Х(1 определяется следующей

( X² —(Х 1) ) ² ) ФР времени технологического процесса. В формулой:

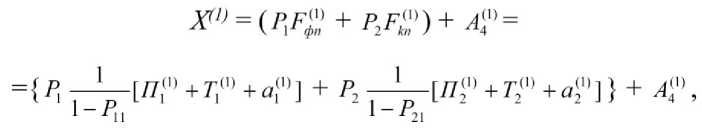
где ^{P 1} - вероятность того, что при выполнении операций поиска документов будет реализовываться фактографический поиск, а ^{P 2} ( ^{P 2} = 1- (З)

• ¹    ) - вероятность того, что будет реализовываться контекстный поиск, ⁴ -среднее время анализа аналитиком выходной коллекции документов.

Не представляет затруднений вывод функциональных уравнений и для других технологических процессов, описываемых сетевыми вероятностными моделями. Зная моменты ФР времени подготовки ИАМ (X1 , X2 ), можно легко вычислить, используя соответствующую аппроксимацию в классе двухпараметрических функций [10], и вероятность подготовки ИАМ к заданному сроку.

Наряду с такими базовыми задачами как фактографический и контекстный поиск, выполняемыми в ЛВС информационно-аналитических центров, аналитики часто решают в клиент-серверном режиме такие базовые задачи, как частотный анализ, кластерный анализ и семантический анализ. Приведем функциональные и расчетные соотношения описывающие случайные процессы частотного, кластерного и семантического анализа.

Функциональные соотношения, описывающие базовые операции частотного анализа, имеют вид

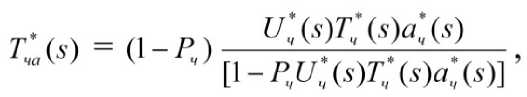
T^) = $e^ia(l)

где                   - преобразование Лапласа-Стильтьеса функции распределения (Тча (t)) времени выполнения операций частотного анализа документов в ЛВС, включая операции на рабочей станции и сервере поиска;

^(s) = j_e *W₄(O, u„(t)

• -    ФР времени выбора на рабочей станции оператором параметров для решения задачи частотного анализа;

со т>) = р-^тч(О, W

• -    ФР времени выполнения операции частотного анализа на сервере ЛВС;

a’(s) = р~и<Ч(0, «Ч(С

• -    ФР времени принятия решения аналитиком о повторе операции частотного анализа;

P

• ^ч    - вероятность повторного выполнения операции частотного

анализа.

Из соотношения (7) легко получить расчетные соотношения для

(T ( 1 )

( ^ча

среднего времени операций частотного анализа документов

Не представляет затруднений вывод функциональных соотношений в терминах преобразований Лапласа-Стильтьеса, описывающих базовые операции кластерного и семантического анализа при подготовке информационно-аналитических документов:

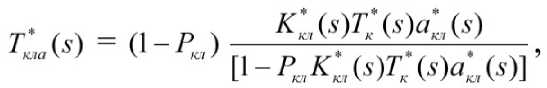
C^R"^.^')

где                   - преобразование Лапласа-Стильтьеса функции распределения времени выполнения операций кластерного анализа документов в ЛВС, включая операции на рабочей станции и сервере поиска,                      - преобразования Лапласа-Стильтьеса функций распределения, соответственно, времени выбора на рабочей станции оператором параметров для решения задачи кластерного анализа времени выполнения операции кластерного анализа на сервере ЛВС времени принятия решения аналитиком о повторе операции кластерного анализа, Pкл - вероятность повторного выполнения операции кластерного анализа.

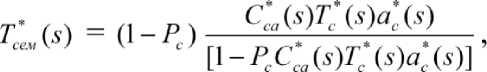
^> = ^-^(1)

где - преобразование Лапласа-Стильтьеса функции распределения времени выполнения операций семантического анализа документов в ЛВС, включая операции на рабочей станции и сервере

„ _ с», m «:м поиска,

преобразования Лапласа-Стильтьеса

функций распределения, соответственно, времени выбора на рабочей станции оператором параметров для решения задачи семантического анализа, времени выполнения операции семантического анализа на сервере ЛВС, времени принятия решения аналитиком о повторе операции семантического анализа, Pс - вероятность повторного выполнения операции семантического анализа.

Из функциональных выражений (9) и (10) можно легко получить ( 1 ) моменты ФР ^кла и ^сем . В частности, математические ожидания ^Tкла и

^{( 1} )

^{T сем} определяются формулами:

С = <й)1.=.=

ГЙ+^+^], О

С = чС(»))’1

4=0 ~

[С + ?;(1)

( 1)

При этом средние времена выполнения операций кластерного ^Tк и

( 1 )

семантическогоT с анализа на сервере ЛВС определяются с помощью вложенной аналитической модели аппаратно-программного уровня, а (1) (1) (1) (1)

параметры ^кл , ^с , ^Ккл , ^Сса , ^акл , ^ас оцениваются статистическими методами на основании серии непосредственных измерений количества повторений и времени выполнения операций в ЛВС на рабочих местах аналитиков при решении ими базисных задач.

Типовой технологический тракт подготовки ИАМ

Рассмотрим типовой технологический тракт подготовки ИАМ на основе рассмотренных выше базовых операций. Пусть технологический тракт включает базовые операции фактографического и контекстного поиска документов, частотного, кластерного и семантического анализа коллекции документов, а также заключительную операцию анализа выходной коллекции документов.

Операции фактографического и контекстного поиска, выполняемые аналитиками при подготовке информационно-аналитических материалов рассмотрены при выводе функционального соотношения (1). Из этого соотношения легко получить преобразование Лапласа-Стильтьеса для функции распределения времени выполнения обобщенной операции «Поиск» - ПОИСK(t):

ПОИСКА) = P ₁ {(1-P ₁₁ )n ₁ *(s)T ₁ * (s)a ₁ * (s) /[1-P_nП₁*(s)T₁*(s/a₁*(s)]}+

+Р ₂ {(1-Р ₂ 1 )П₂Д)Т₂Д)а₂Д)/[1-Р^^

ПОИСК* (s) = f e^ сЦПОИСК^) где                  -                 .

Дифференцируя функциональное соотношение (13) по s можно легко получить расчетные формулы для моментов ФР ПОИСКА). В частности, среднее значение операции «Поиск» ( ПОИСК ¹¹ ) рассчитывается по следующей формуле:

После завершения обобщенной операции «Поиск» аналитиком принимается решение о дальнейшей обработке коллекции документов найденной в соответствии с заданными им предписаниями на фактографический и контекстный поиск информации, (операция анализ А1 , ФР длительности этой операции ^А i ⁽ t ) ). После завершения операции А1

с вероятностью Р 1 _Ч коллекция документов передается на частотного анализа ЧА (ФР ^Тча ⁽ t ) ), с вероятностью Р 1кл - на кластерного анализа КЛА (ФР ^{Ты а (} t ) ), с вероятностью Р 1с - на

операцию

операцию

операцию

семантического анализа СА (ФР ^Тсем ⁽ t ) ) и с вероятностью Р 1 _К - на операцию экспертного анализа выходной коллекции документов АКД (ФР AK(t) ). При этом выполняется условие нормировки Р 1 _Ч + Р 1кл +Р 1с + Р 1к =1.

После выполнения операции частотного анализа аналитиком принимается решение о дальнейшей обработке документов (операция анализ А2 , ФР длительности этой операции А ² ( t ) ). После завершения операции А2 с вероятностью P 2кл коллекция документов передается на операцию КЛА , с вероятностью P 2с - на операцию семантического анализа СА и с вероятностью P 2к - на операцию АКД ( P 2кл + P 2с + P 2к =1 ).

После выполнения операции кластерного анализа аналитиком снова принимается решение о дальнейшей обработке документов (операция анализ А3, ФР длительности этой операции - А3 (t)). После завершения операции А3 с вероятностью P3с коллекция документов передается на операцию семантического анализа СА и с вероятностью P3к - на операцию АКД (P3с+P3к=1). И, наконец, после завершения операции СА всегда выполняется операция АКД – экспертный анализ выходной коллекции документов.

Функциональное уравнение, определяющее преобразование Лапласа-Стильтьеса ФР времени подготовки информационно-аналитических материалов ИАМ 1 (t) в соответствии с рассмотренной выше вероятностной сетевой моделью типового технологического тракта, можно получить воспользовавшись функциональными соотношениями (7), (9), (10), (13),

С (О , С (-0, С (5), ПОИСК*^) определяющими                               :

HAMiys)=nOHCK*(s)A*(s) {PiKAK* O+PicT^O) АКИН

+р_1кят;_ю(з) а^ИзиКо) AK*(_S)+P_3kAK*(s))+ ^Р1_Чт:,^ АУ^^АК^+Р.сТС,^ ак*о)+

= ПОИСК* (s) A* (s) {Р!к+Р1сТСО+ Р/чПХО УОЛРгк+РгсТСОСН

+(Р^ + Р1ч Ргкл Т*_о (s) A, (s) )[ 7^_а О) X О’) (Р_3с тС (s) + ^)]+

+ Р_1чТ:_а 0) У 0) (Р₂ЛР2_С ТС (8))} АН О) ■

Дифференцируя (15) по s, получим следующее соотношение для расчета среднего времени подготовки ИАМ1 (ИАМ1 ):

ИАМ" = ПОИСКА + А" + Р1Ч (Т" + А? )+(Р^ + Р1Ч Р2кл )[ Т" + А^ ] +

+( Р_1с + Р_1ч Р_2с + Pn Р_2к Рзс ) Т^ + АК^.

⁽ 1 )       ⁽ 1 ) у( 1 )

Средние значения ПОИСК(1), Tча , Tкла, Tсем оцениваются на основании параметров ФР типовых базовых операций с помощью соотношений (14)

(8), (11), (12).

Не представляет затруднений оценка на основе функциональных соотношений (7), (9), (10), (13), (15) не только среднего значения ФР ИАМ 1 (t) , но и второго момента и дисперсии этой ФР.

Обычно для подготовки итогового информационно-аналитического документа ИАМ1Σ требуется подготовить несколько ИАМ1 в соответствии с рассмотренным (или похожим) типовым технологическим трактом. При этом обычно известно (определяется на основе статистических данных) распределение дискретной целочисленной функции количества ИАМ1 подготавливаемых при разработке ИАМ1Σ . Тогда распределение Лапласа-Стильтьеса ФР времени разработки ИАМ1Σ определяется следующим соотношением:

где - вероятность того, что при разработке итогового ИАМ1Σ необходимо подготовить Ki ИАМ1 по рассмотренной выше первой технологической схеме (i =1,n).       .

Моменты ФР времени разработки итогового документа ИАМ 1 Σ можно определить, дифференцируя выражение (17) по s. В частности, среднее время разработки итогового документа ^{ИАМ 1 Σ} равно:

При этом оценка ^{ИАМ 1} производится с помощью соотношения (16) а вероятности (i=1,n) оцениваются на основании статистических данных по разработке итоговых информационно-аналитических материалов за длительный промежуток времени (порядка нескольких лет).

Не представляет затруднений вывод функциональных уравнений и для других технологических трактов подготовки информационноаналитических материалов, описываемых сетевыми вероятностными моделями. Рассчитав первый и второй моменты ФР времени подготовки ИАМ в соответствии с определенной сетевой вероятностной моделью ^{( 1} )               ( 2 )

технологического тракта (например ^{ИАМ 1} , ^{ИАМ 1} ) и определив первый и второй моменты ФР длительности разработки итогового документа ( ¹ )                   ( ² )

(например ^ИАМ1Σ , ^ИАМ1Σ ), можно легко вычислить и вероятность подготовки ИАМ или разработки итогового документа к заданному сроку, используя соответствующую аппроксимацию в классе двухпараметрических функций.

Заключение

В работе получены следующие результаты:

• -    Проведен анализ сетевых вероятностных моделей исследования типовых технологических схем выпуска информационноаналитических материалов (ИАМ) в вычислительных центрах построенных на базе локальных вычислительных сетей.

• -    Разработан математический аппарат для аналитического исследования вероятностных сетевых моделей анализа временных характеристик процессов подготовки ИАМ. Получены функциональные уравнения и расчетные соотношения, позволяющие провести многовариантный анализ различных схем подготовки документов и выявить узкие места основных типовых технологий подготовки ИАМ.

• -    На базе теории случайных процессов получены достаточно универсальные расчетные соотношения для анализа вероятностновременных характеристик типовых процессов подготовки ИАМ, которые могут представлять интерес для широкого круга специалистов.