Вероятностный подход к оценке характеристик состояния экосистем по показателям нереализованных возможностей

стных математических образов и отношений между ними, не противоречащих результатам опыта; 2) познание и описание математических закономерностей на основе количественно-прогностических отношений. Первое влияет на эффективность хозяйственной и экономической деятельности, второе – позволяет совершенствовать и оптимизировать принципы переработки информации о количественных оценках состояния явлений и процессов.

Успешность решения подавляющего большинства природоохранных задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов и их воздействий на экосистему. Хозяйственная деятельность и природные явления обуславливают распределение и взаимную увязку имеющихся ресурсов, представляющих сырье, оборудование, деньги, рабочую силу, электроэнергию, топливо, материалы и другие факторы воздействия. Оптимальность их влияния определяется естественными ограничениями на потребление ресурсов. Таким образом, при математическом моделировании экологических процессов необходимо выполнить следующие действия:

• -    уяснить механизм оценки природоохранных технологий и состояния экосистем, сформулировать цель решения экологической задачи методами теории вероятностей и математической статистики;

• -    оценить экологическую ситуацию и определить составляющие достижения поставленной цели;

• -    выбрать приоритетные численные показатели для оценки экосистемы;

• -    построить вероятностно-статистическую математическую модель исследуемого процесса, устанавливающую функциональные зависимости между показателями и результатами;

• -    осуществить исследование анализируемого объекта с помощью математической модели соответствующим методом;

• - проверить соответствие полученных результатов решения реально существующим экологическим показателям;

  - использовать полученную модель в планировании экологических мероприятий и прогнос-

  
  

  который задается соотношением:

  
  

  тических расчетах.

  Следовательно, для повышения эффективно-

  
  

  сти управления природоохранными мероприя-

  
  

  Сц  — 2 l L , x - — m x- )( x , — m J

  f ⁽ x 1 , x 2 ,..., x n ⁾ = -------e    ' - ^{1 j} - ¹                  , (5)

  ( 2 ^ ) 2

  
  

  тиями, на основе количественных оценок состояния экосистем, технических и инженерных объектов требуется адаптация математического

  
  

  инструментария к указанному классу задач, в

  
  

  здесь | C | - определитель матрицы С , С = || c i, || - матрица, обратная корреляционной матрице

  
  

  которых оперируют системами непрерывных или дискретных случайных величин ( X 1 , X 2 ,..., X n ) .

  Числовыми характеристиками для указан-

  
  
  
  
  

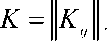
  ной системы являются:

  
  

  • -    n математических ожиданий m , m , ..., m ; x ₁ x ₂         x _n

  • -    n дисперсий D x 1 , D x 2 ,..., D x n ;

  • -    n • ( n — 1) корреляционных моментов K i, , где i ^ j = 1, 2,..., n .

  Корреляционные моменты характеризуют попарную корреляцию всех величин, входящих в систему и имеют вид:

  
  

  Элементы матрицы c

  
  

  ij

  
  

  ₌ (_ 1) i * > M2L

  ^{( )}     K I

  
  

  K – определитель корреляционной матрицы, а

  
  

  М: ij

  
  

  – миноры этого определителя, причем

  
  
  
  

  K ij = M XX

  
  

  X - = X ^— m X. = X , ^— m j . (1)

  
  

  IС =J

  ^K

  
  

  Следует отметить, что дисперсия каждой из случайных величин X i есть частный случай корреляционного момента X i на саму себя, действительно:

  
  

  Из выражения (5) в качестве примера можно получить закон нормального распределения плотности случайных величин при n = 2 , то есть на плоскости для ( X , Y ) .

  Корреляционная матрица при этом принимает вид

  
  

  D i = K -j = M

  
  

  ^X i ²

  
  
  
  

  = M X.X.

  
  
  
  
  
  

  K =

  
  

  а ²

  x

  
  

  Все корреляционные моменты и дисперсии представляют в виде корреляционной матрицы.

  
  

  аа r

  x y xy

  
  

  аа r 2

  x y ^xy

  а ² y J

  
  

  .

  
  
  
  

  K =

  
  

  f K

  
  

  K 21

  
  

  ^K 12

  K 22

  
  

  ...   K 1 n

  ...   K 2 n

  
  

  . где ^K y = ^Kn . ⁽³⁾

  
  

  ...

  
  

  ...

  
  

  ... ...

  
  

  I K 1

  
  

  K n 2

  
  

  ... K_nn J

  
  

  Обычно вместо этой матрицы составляют нормированную матрицу из коэффициентов кор-

  
  

  реляции.

  
  

  r 11     r 12

  r 21     r 22

  
  

  .

  
  

  .

  
  

  .

  
  

  r 1 n )

  
  

  .

  
  

  .

  
  

  .

  
  

  r

  2 n

  
  

  .

  
  

  .

  
  

  .

  
  

  ...

  
  

  , где r j

  
  

  K

  j

  , причем

  
  

  rr

  n 1 n 2

  r, = r,, = ... = r = 1.                          (4)

  11       22                 nn

  Если система непрерывных случайных величин ( X 1 , X ₂ ,..., X n ) характеризует некоторую экосистему в n- мерном пространстве показателей, то она может быть описана нормальным законом распределения плотности вероятности,

  
  

  .

  
  

  .

  
  

  .

  
  

  r

  nn

  
  

  j

  
  

  Отсюда I K I = а> у ^{2( 1 —} r² y Ц

  
  

  I С =

  
  

  а Or² ( 1 — r ² ) x y xy

  
  

  С =

  
  

  I , ¹ X а ² ( 1 — r ² ) x xy

  — r xy аа ( 1 — r 2 ) \ x y X xy /

  
  
  

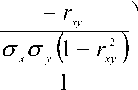
  а

  ^y

  _—

  r ² xy

  
  

  . (7)

  
  

  Подстановкой элементов определителя матрицы С в (5), получают выражение для нормального закона на плоскости.

  
  

  f ⁽ x , y ⁾ =

  
  

  2 ^аа _Л/1 — rr x y xy

  
  

  1 [ ( x — mx!

  
  
  

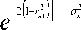
  ² r x, ⁽ x ^— m x ) ⁽ y - m y ) ⁽ y ^— m y ) ^{2 а} . ^а ,     ⁺  °y

  
  
  
  

  Из соотношения (8) следует, что нормальный закон на плоскости зависит от пяти параметров, имеющих следующий вероятностный смысл:

  - m , m – математические ожидания; xy

  - а x , а _y - средние квадратичные отклонения;

  - r xy – коэффициент корреляции величин X и Y.

  
  

  r xy

  
  

  K xy

  а а '

  xy

  
  
  
  

  Коэффициент корреляции обращается в ноль для независимых случайных величин. Если коэффициент r xy не равен нулю, то случайные величины являются не коррелированными.

  Если r xy ^ 0 , то случайные величины ( Х, Y) зависимы и условные законы распределения

  
  

  ^ 2,0 = ^M

  
  

  X ²

  
  

  Y ⁰

  
  
  
  

  ^ 0,2 = ^M

  
  

  X ⁰ Y ²

  
  

  = M X ²

  
  

  = M Y ²

  
  

  = D [ X ] , (18)

  
  

  = D [ y ] . (19)

  
  

плотности вероятности принимают вид f (У / x) и f (x / У):

, x                          _ 1___fy- my - x- mx f ну/х\ = fxJ =______1_____t.t "y rxy " J

f(y / x) f( x) " г ^e              , y xy f (, / y)= Йы)= f2 ( у )

1 I x - m ,      x - m y )

IГ I e 2(1-rxy) t "x     y  "у

"x V^{1 -} ^У ^

Это условные плотности вероятности

(11) нор-

мального закона с центрами рассеивания my /x = my + rxy ~ (x - mx ),(12)

"x mx / y = mx + rxy ” (У - my ) .(13)

"

и средними квадратичными отклонениями

"y / x = "y V(1 - r. ) ,

"x / y = "x (1 - rxy ) .

В работе [1] подробно изложен механизм вероятностной характеристики распределения дискретных величин для оценки результативности природоохранных мероприятий согласно различных технологий и состояния экосистем по показателям нереализованных возможностей на примере одномерного случая.

Когда имеет место система двух случайных величин, то первые начальные моменты являются математическими ожиданиями величин X и Y системы, то есть mx = «10 = M [X 1Y0 ] = M [X ],    (16)

m y = « 01 = M [ X ⁰ Y ¹ ] = M [ Y ] .     (17)

Совокупность математических ожиданий m x и my представляет характеристику положения системы. Геометрически это координаты точки на плоскости, вокруг которой рассеяны значения системы (Х, Y). Два вторых центральных момента системы представляют дисперсии величин Х и Y и характеризуют рассеивание случайных точек в направлении осей Ox, Oy .

Второй смешанный центральный момент имеет специальное обозначение

^ ;, = K y = M XY = M [ ( X - m x ) - ( y - m y ) ] .(20)

y

и представляет корреляцию между случайных величин Х , Y.

Для дискретных и непрерывных случайных величин корреляционный момент выражают соответственно формулами

Kxy = ZZ (x.- mx ) • (У, - my ) • Pj , ij

^Kxy = J J ^{( x - m}x ⁾ • ⁽ У ^- m y ⁾ • ^{f (} x , У ⁾ dxdy. ⁽²¹ )

-TO

Он наряду с рассеиванием величин Х и Y характеризует связь между ними и независимых случайных величин равен нулю, то есть K = 0. xy

Если K _xy # 0 , то между случайными величинами есть вероятностная зависимость.

Для характеристики нереализованности оптимальных показателей состояния экосистемы используем величину d

S k = ( X k - Z k ) ,           (22)

где X k – случайная величина, Z k – регламентированное значение для оптимального состояния системы, к = 1 , 2 ,...,n .

В этом случае начальный момент первого порядка показателя S _k принимает вид для дискретных и непрерывных случайных величин n

« 1 ^(S k ⁾ = Z ^{( x} k ^- Z k ⁾ pi t ;      (23)

I =1

J

« 1 ( ^S t ⁾ = J ^{( x -} Z t ⁾ f t ^{( x ) dx} .     (24)

-J

Второй вариационный момент, характеризующий разброс значений статистических параметров относительно Z k

n

М 2 ( S t ) = Z ( x . - Z t ) ² P k ;      (25)

=1

J

М 2 ^(S t ⁾ = J ^{( x -} Z t ^{) 2} f t ^{( x ) dx} . ⁽²⁶⁾

-

Здесь p_tk ^- вероятность P ( ^X _k = x k ⁾ = P k . fk ( X ) — распределение плотности вероятности случайной величины X k .

Для системы двух случайных величин (X, Y) с показателями оптимальности (Z,, Z , ) указанные характеристики принимают вид nn

« 10 ⁽⁵х ) = S ^{( X} - "  ^Z x ^Р> « 01 ⁵ ) = S ⁽ У - "  ^Z y ) Р . i = 1 j = 1

где « < 5, < ^. Г ^ 5, < V.

Аналогично, вероятность попадания значений системы ( 5 , , 5 , ) в эллипс рассеивания B t .

отношение полуосей которого t =

«, 5)

«у 5 )

, равна

t ²

Р 5 , , 5 , ⁾с B, ⁾ = 1 — e к.      ⁽²⁹⁾

то                                                        то

« 10 ^{( 5} x ⁾ = J ^{( ,} - Z x ⁾ f . ^{( , )} dx , « 20 ^{( 5} У ⁾ = J ⁽ У - ^Z, ^f 2 ⁽ У ⁾ dy .

—то                                           —то

n n                       nn

« 20 ( 5 , ) = SS ( X — Z , ) 2 P j , Л( 5 , ) = SS , — Z y ) ² Р..

- = 1 j = 1                                                  i = 1 j = 1

« 11 ^{( 5} ,y ⁾ = ^K„ ^{( 5} ,y ⁾ = S S ⁽ x - ^— Z , ^{) (} У j ^— Z y ^Р .

i = 1 j = 1

то то

« 1 1 ^{( 5} ,У ⁾ = ^K ,y ^{( 5} ,У ⁾ = J J ^{( , —} Z , ^{) (} У ^{— Z} y I f ^{( ,} , У ^{) d,d}У .

—то—то

Здесь Р , = P ( X = , 1 , Y = y j ⁾ . f ( , , у ) -функция распределения плотности вероятности системы непрерывных случайных величин.

В дальнейшем после перехода от системы двух случайных величин ( X , Y ) к системе ( 5 , , 5 _у ) . для которой справедлив нормальный закон распределения на плоскости, можно рассчитать вероятность оптимального функционирования системы в заданной области D изменения параметров ( X , Y )

Если , = 1 . когда эллипс рассеивания вырождается в круг и случайные величины 5 , , 5 y не

1 коррелированны Р (( 5 , , 5 , ) с B 1 ) = 1 — e ² = 0 , 393 , при , = 2 Р (( 5 , , 5 , ) с B ₂ ) = 0 , 865 . .

Таким образом, соотношения (28) и (29) позволяют на практике получать вероятностные количественные характеристики оценки приближения исследуемой системы к оптимальному состоянию.

Р((5,,5y)с D)= JJ f (5,5y)d5,d5y =

D

2.ка^т

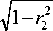
JJ‘

D

( 5 , — « ₀ ) ^{2 2} Г , ( ⁵ , — « 0 ) ( ⁵ , — « 02 ) ( ⁵ , — « 02 ) ² dxdy

^           «, « 2       ⁺      « 2

II---- г ~ «11

где: «1 = «21м ; «2 = л/«02 ; r12 “ « « •

Конечный количественный результат опре-

деляется заданной областью D, в которой изменяются составляющие системы ( 5 , , 5 _y ) .

Например, для прямоугольной области D со

сторонами, параллельными координатным осям и нормальном законе распределения системы ( 5 , , 5 , ) вероятность

^{Р (( 5} , 5 , ) с D ⁾=

(

ф

V

ф

(⁵ ,

m5, x

« ,

5^х)

ф

( 5« — m5,

I «, ^’х )

5 — ms

Y 5 ,

«У 5 )

—

( 5v — m5, )

V ,\ ,/ 7