Вещественные n-поверхности в пространствах R (e)

Вещественные п-поверхности Vˆn пространства Rn (e) изображаются в пространстве Rе2n n-поверхностями. Репер R = {X, Ji, Jn+i}, где X - точка поверхности Vn, a Ji, Jn+i - векторы, определяемые соотношениями (1), является каноническим репером поверхности Vn пространства Rе2n. Формы имеют вид:

an ⁺ j —   + j ak   nn + j _ / "+ j

^vi       ^uik ^v , ^uik ^uki .

Так как репер R - канонический, то функции ф', bn+j образуют полную систему инвариантов поверхности Vn биевклидова пространства гиперболического типа Rе2n и определяют ее с точностью до движений пространства Rе2n и, следовательно, вещественную поверхность Vˆn пространства Rn (e) с точностью до движений этого пространства. При проектировании поверхности Vn на главные плоскости Rn и Rn получим области Q+ и Q_.

Пусть V n - поверхность постоянных стационарных углов, т.е. ф ш = const . Тогда dф _i = -0 n ⁺ ' = 0 , из (1) следует b n⁺' = 0 . Если сеть Е n является геодезической, то имеем b n⁺' sin 2ф j + b in⁺' sin 2ф_{ = 0 . Отсюда вытекает, что b in⁺' = 0, ( ' ^ j ) . Но так как b in⁺i = 0, то векторы нормальной кривизны линий 0 ' сети Е n равны нулю, т.е. b ii = 0 . Обратно, если у линий 0 ' сети Е n векторы нормальной кривизны равны нулю, то b ii = 0 , т.е. b in^{+ j} = 0 . Тогда следует а'_{ = 0 , т.е. векторы относительной кривизны <2 ii линий 0 ' сети Е n равны нулю и поэтому сеть является геодезической. Отсюда следует

Теорема 1 Сеть Е n поверхности V n постоянных стационарных углов биевклидова пространства гиперболического типа Rе 2n является геодезической тогда и только тогда, когда векторы нормальной кривизны линий сети Е n равны нулю.

Пусть V _n - поверхность равного наклона. Тогда отображение T является конформным и в силу обобщенной теоремы Лиувилля [38] поверхность является при n>2 алгебраической.

Теорема 4.2 . Минимальная поверхность V_n равного наклона в биевклидовом пространстве гиперболического типа Rе 2n является плоскостью.

Доказательство . Пусть поверхность V_n равного наклона является минимальной. Тогда вектор М             средней кривизны равен      нулю,      т.е.

М = 1У — = 1У (b^ + b £ + - + b"^ i) J „+i = 0.          Отсюда          следует ni ni n+i      n+i              n + i                                 n+i       n+k       n + j       n+k                n+k       n+k bw + b 22 + •"+ bnn = 0. Получим bik = bii = Ь/ = Ь. , т.е. bu = b. . Тогда следует bii+k = 0, следовательно, bik+i = 0. Но из (2.32) b”.+i = -b„+j. Поэтому by+j = 0. Получим, что все компоненты асимптотических форм равны нулю, т.е. минимальная поверхность Vn равного наклона является при n>2 плоскостью.

При ф = % поверхность равного наклона является антиголоморфной, а конформное отображение Т является изометрией, так как коэффициент k = tgф = 1 , т.е. антиголоморфная поверхность V_n является плоскостью.

Рассмотрим случай n=3, т.е. поверхность V3 в пространстве Rе6. Пусть поверхность равного наклона. Тогда следует: 456 4  4456  55

и 11   ^12   ^13     ^22     ^33,  ^12   ^22   ^23     И1^33

456 66456

и 13   ^23   ^33     ^11     ^22,  ^23   И3   ^12

Отнесем поверхность   V3   равного наклона к сети линий кривизны относительно вектора J4. Так как всегда имеет место b23 • J4 = 0, то должны выполняться условия —  —      —  —                      44      —       —  — —— b12 • J4 = 0,    b13 • J4=0.   Отсюда   следует   b12 = b13=0,    b23 = 0,   b12 II J5,b13 II направления J2 и J3 сопряжены. Тогда векторы нормальной кривизны линий сети Е3:

—•       —*       —*        —*         —*        —*               —*        —*

bX1 II b22 II b33 II J4 и bxx + b22 = 0, bX1 + b33 = 0. Уравнение присоединенной поверхности в точке Х поверхности V3 равного наклона имеет вид

( b^y ⁴1)• (( b⁴y ⁴ +1)• ( b⁴y ⁴ -1) + ( b⁴y ⁶) ² + ( b⁴y ⁵) ² ) = 0 или          b⁴y ⁴ +1 = 0,

( y ⁴) 2 + ( y ⁵) 2 + ( y ⁶) 2 = 1 , т.е. присоединенная поверхность представляет собой сферу с центром в точке Х и радиуса 1 плоскость П , касательную к сфере в точке b 1⁴1

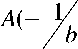
43   53   45

θ ₃ = - θ ₁ tgϕ ₁ , θ ₃ = - θ ₂ tgϕ ₂ , θ ₁ = - dϕ ₁ , θ ₂ = - dϕ ₂ ,

θ 6⁴ =- θ 1⁶ ctgϕ 1 , θ 5⁶ =- θ 2⁶ tgϕ 1 , θ 3⁶ =0,

₂   θ ₁ ⁵ sin 2 ϕ ₂ + θ ₂ ⁴ sin 2 ϕ _{1    5}   θ ₁ ⁵ sin 2 ϕ ₁ + θ ₂ ⁴ sin 2 ϕ ₂

, ₄

2(cos ² ϕ ₁ -cos ² ϕ ₂ )         2(cos ² ϕ ₁ - cos ² ϕ ₂ )

θ=

6     6     6               —   —         —   —         ——

Отсюда следует b₁⁶₃ = b₂⁶₃ = b₃⁶₃ = 0 , тогда b₃₃ ⋅ J₆ = 0, b₁₃ ⋅ J₆ = 0,   b₂₃ ⋅ J₆ = 0,   т . е .

векторы вынужденной кривизны полей J₁ и J₂ вдоль 1- голоморфной линии θ³ и ее вектор нормальной кривизны ортогональны 0- голоморфной нормали [X, J₆] (1,0) - полуголоморфной поверхности V 3 . Пусть ϕ₁ = const, ϕ₂ = const, тогда из (4.3) следует 45     444   55 5

θ1 = θ2 = 0,  т.е.   b11 = b12 = b13 = 0,   b12 = b22 = b23 = 0 . Если сеть   Σ 3   является геодезической,     то из (2.22) следует     b151 ⋅ sin 2ϕ2 = 0,     b242 ⋅ sin 2ϕ1 = 0,

4                   —            5                   —                                                                                                                                  *          *           *

b ₃ ⁴ ₃ ctgϕ ₁ J ₁ + b ₃ ⁵ ₃ ctgϕ ₂ J ₂ = 0 . Так как ϕ ₁ , ϕ ₂ ≠ 0, ^П2, т.е. векторы b ₁₁ , b ₂₂ , b ₃₃ линий сети Σ ₃ коллинеарны вектору J ₆ . Верно и обратное. Отсюда следует

Теорема 3 . Сеть стационарных углов (1,0)-полуголоморфной поверхности V 3 , постоянных стационарных углов пространства Re 6 является геодезической тогда и только тогда, когда вектор нормальной кривизны 1-голоморфной линии равен нулю, а векторы нормальной кривизны двух других линий этой сети коллинеарны 0-голоморфной нормали.

Основная система дифференциальных уравнений имеет вид:

d_i ⁴ _j ∧ θ^j = M_keθ^k ∧ θ^e , db_i ⁵ _j ∧ θ^j = M_keθ^k ,

db ₁ ⁶ ₁ ∧ θ ¹ = db ₁ ⁶ ₂ ∧ θ ² = K_ijθⁱ ∧ θ^j , db ₁ ⁶ ₂ ∧ θ ¹ + db ₂ ⁶ ₂ ∧ θ ² = C_ijθⁱ ∧ θ^j ,

Характеры s ₁ = 8, q = 15, s ₂ = 5, s ₃ = 2, число Картана Q = 24 , а число существенных параметров N = 24 . Система в инволюции, т.е. (1,0)-полуголоморфная поверхность V 3 пространства Re 6 существует с произволом двух функций трех аргументов.

Пусть ϕ ₃ = 0, ϕ ₂ = ^П2, ( ϕ ₂ ≠ 0,^П 2) тогда поверхность V 3    является (1,1)-

— — — — — — — — полуголоморфной. Из (2.1-2.2) следует J3 = E3+, J2 = E2+, J5 = E2-, J6 = E3- т.е. нормальная плоскость N3 (X) является (1,1)-полуголоморфной, формулы (2.14) принимают вид:

3566   4    2  4

θ ₂ = θ ₂ = θ ₃ = θ ₅ = 0, θ ₁ = - dϕ ₁ ,   θ ₁ = - θ ₂ ctgϕ ₁ ,

θ 1³ =- θ 3⁴ tgϕ 1 , θ 4⁵ =- θ 1⁵ ctgϕ 1 , θ 4⁶ =- θ 1⁶ tgϕ 1 .

Из (5) следует a ₂ ³ ₁ = a ₂ ³ ₂ = ³ ₂₃ = 0 , т.е. на касательных к 1-голоморфной линии θ ² и 0-голоморфной линии 9 ³ существует всего по одному псевдофокусу и векторы <2 22 и <2 ₃₃ относительной кривизны к этим линиям параллельны вектору J 1 причем векторы <з ₂₂ и а₃₃ относительной кривизны полей J ₁ и J ₁ вдоль линий θ ¹ параллельны также вектору J ₁ . Проекциями (1,1)-полуголоморфной поверхности на главные плоскости R ₃ ⁺ и R ₃ ^- является 2-поверхности V ₂ ⁺ и V ₂ ^- .

Основная система дифференциальных уравнений имеет вид:

db j л У^j = M ke y k л У^е , db 1⁵1 л У ¹ + db f₃ А У³ = N k y A y e , db f₃ л У¹ = db ₃3₃ л У³ = S ke y k л y e , db ^ л У ¹ + db ^ л У² = L ke y k л y e ,

db 1⁶₂ л У¹ = db 22 л У² = R ke y k л y e

Тогда rangM 1 = 7, rangM ₂ = 11, и характеры s 1 = 7, s ₂ = rangM ₂ — rangM 1 = 4, s ₃ = 1, Q = N = 18 - Поэтому (1.1)-полуголоморфная поверхность V ₃ в пространстве Re₆ существует с произволом одной функции трех аргументов.

Если ф₁ = П4 , то (1.1)-полуголоморфная поверхность V 3 является CR -поверхностью. Тогда dф₁ = 0 и из (4.5) следует У⁴ = 0, т.е. b ₁ ⁴ ₁ = b ₁ ⁴ ₂ = Ь 1⁴ = 0 . Формы У ², У³ имеют вид 2    42  43   3    42  43

У 1 = —( b ₂₂ У + b₃₃У ), У 1 = —( b₂₃У + b₃₃У ), т.е. инварианты сети а 11 = a ₁₁ = 0 . Отсюда следует, что вектор относительной кривизны <2 11 антиголоморфной линии У ¹ равен нулю, т.е. линия У¹ - геодезическая. Так как вектор нормальной кривизны антиголоморфной линии У¹ (1,1)-полуголоморфной поверхности V 3 ортогонален вектору J ₄ . Нормаль [ X , J ₄ ] является антиголоморфной. Поэтому верна

Теорема 4 . Если поверхность V 3 пространства Re 6 является CR -поверхностью, то антиголоморфная линия У¹ сети стационарных углов является геодезической, а ее вектор нормальной кривизны ортогонален антиголоморфной нормали.

Из системы (6) имеем rangM 1 = 6, rangM ₂ = 9 и характеры s 1 = 6, s ₂ = 7, q = 9, s ₃ = 0 . Число Картана Q = 12, а N = 12 . Тогда произвол существования CR -поверхности V 3 пространства Re 6 равен трем функциям двух аргументов.

Пусть ф ₂ = ф ₃ = 0, ( ф ₁ ^ 0, П2) , тогда поверхность V 3 пространства Re₆ является (2,0)-полуголоморфной поверхностью. Ее нормальная плоскость N ₃ ( X ) является (0,2)-полуголоморфной. Система (4) принимает вид: 24  34  55  66

У =— У 2 ctg9 i , У 1 =— У 3 tg ^, У 4 = — У 1 ctg ^, У 4 = — У 1 tg ^,

у:

^™1

■ dф₁, У ₂ ⁵ = У ₂ ⁶ = У ₃ ⁵ = У ₃ ⁶ = 0.

66666  55555

Отсюда следует b i2 — b 22 — b i3 — b 23 — b 33 — 0, b i2 — b 22 — b i3 — b 23 — b 33 — 0. Т ак как by ■ J ₅ = 0, by ■ J ₆ = 0, ( i ^ j ) , то есть Е ₃ является сетью линий кривизны относительно любого вектора из плоскости [ X , J ₅ , J ₆ ] , т.е. является сетью линий кривизны относительно любой 0-голоморфной нормали.

Из (7) имеем У ₁ ² =— ( b ₁ ⁴ ₂ У ¹ + b 22 л У ² + b 23 л У ³) ctg ф ₁ , У ₁ ³ =— ( b ₁⁴3 y ¹ + b 23 л У ² + b ₃ ⁴ ₃ л У ³) ctg ф ₁. Отсюда следует, что инварианты сети Е ₃ 24   24   24   34

имеют вид:     a ₁₁ =— b ₁₂ ctgф₁,    a ₁₂ =— b ₂₂ ctgф₁,    a ₁₃ =— b ₂₃ ctgф₁,    a ₁₁ =— b ₁₃ ctgф₁,

^3

N2(X) является двумерной и Ф6 — ЯФ , где Я = b6 I b^.. Векторы J4, J5 + ЯJ6 образуют базис плавной нормали (2,0)-полуголоморфной поверхности    V3. Заметим, что присоединенная кривая (2,0)-полуголоморфной поверхности V3 является кривой третьего порядка. Пусть сеть Е3 является сетью линий кривизны относительно вектора J4, тогда b162 — bi3 — b23 — 0 и   b12 — b13 = b23 = 0, ан = 0,  т.е. сеть Е3 является сетью линий кривизны с одним семейством геодезических линий 01. В этом случае присоединенная кривая распадается на две параллельные прямые 1 - b22 у4 = 0, 1 - b33 у4 = 0 и прямую 1 -b4у4 -(b5 + Л?!!) = 0. Если вектор J5 принадлежит плоскости главной нормали, то Я = 0. Поэтому b6 = 0. Репер R становится каноническим и формы 02,056 являются главными, т.е. 02 — а20, 056 = а601. Полную систему инвариантов образуют одиннадцать функций ф1, bi4, b151, а2i, а6 и они определяют (2.0)-полуголоморфную V3 поверхность пространства Re6 точностью до движений этого пространства.

Если ф1 — П4 , (2,0)-полуголоморфная поверхность является CR-поверхностью. Тогда из (7) следует   04 = 0   т.е.   b141 = b42 — b143 = 0.   Тогда а 2 = <3 = 0. Поэтому антиголоморфная линия 01 является геодезической и ее вектор нормальной кривизны ортогонален вектору J4 , т.е. для этой поверхности верна теорема 4.4.

Пусть ф3 — 0, ф2 — П2, (ф2 ^ 0, П2), тогда поверхность 1Л является I-голоморфной, ее нормальная* плоскость А£[л) является 2-голоморфной. Система (4) принимает вид 23644566

01 — 01 — 01 , 02 — 03 — 013 — 0,  04 — 05 — 0 .(8)

т7       7       ГХ     1 7 6    3      К     7^4 7   I 7.5 Т      7       16    3      L       7.6

Тогда   bn ^{— b} 13 — 0 , Ь 23 — Ь 23 • ^J 6 ,   ^Ь _п — ^Ь _п • ^J 4 ^{+ Ь} _п • ^J 5 ,   b 22 — b и • ^J 6 ,   b 33 — b 33 • ^J 6 .

Отсюда следует, что 1-голоморфная поверхность V3 допускает поле 1-направлений сопряженное ортогональному ему    2-направлению    [J2,J3] .    Так как

3          3     6 3     5 3

VJ6 — np • dJ6 — 04J4 + 06 J5 — 0, то вектор J6 переносится параллельно в связности нормального расслоения. Векторы нормальной кривизны 0-голоморфных линий 02 и 03 сети Е3 параллельны между собой и параллельны вектору J6. Так как 012 — 013 — 0, то вектор относительной кривизны 1-голоморфной линии 01 равен нулю, т.е. ап — 0 и эта линия является геодезической и лежит в плоскости [X,Jр...,J6], т.е. является гиперплоской. Векторы <312 — а13 — 0, т.е. вектор Jt переносится параллельно вдоль линий 02 и 03 сеть Е3 получебышевская . Так как гапд (0“) — 2,, то 1-голоморфная поверхность V3 является тангенциально вырожденной поверхностью ранга 2. Но <3^ — <3д"2 — 0 1-голоморфная поверхность V3 пространства Re6 расслаивается в 1-направлении {01} на 0-голоморфные 2-поверхности, несущие сеть линий 02 и 03 [15]. Так как число линейно независимых векторов bij равно двум, то главная нормаль двумерная. Вторые квадратичные формы Ф4 — b141(01)2, Ф5 — b151(01)2 и Ф5 — ЯФ4, где Я — b151 /b141. Тогда 3                                            3                             I                           3                                         3                                                                              3                             3               3

b ₁₁ — b ₁ ⁴ ₁ ( J ₄ + ЯJ ₅ ), b ₂₂ — b ₂₂ J ₆ и векторы J ₄ + ЯJ ₅ , J ₆ образуют базис главной нормали N ₂ ( X ) 1-голоморфной поверхности V ₃ . Присоединенная кривая распадается на прямую

1 - ( b ⁴ + ЯЬ ³) у⁴ — 0

и

пару

параллельных

прямых

[ ( b 22 b ₃⁶3 -( b 2₃ ) 2 ) ] ( y ⁶) ² -( b 262 + b ₃ ⁶ ₃ ) y ⁶ + 1 = 0 . Формы кривизны Q 4 ,Q 4 ,Q 6 нормального расслоения равны нулю, т.е. 1-голоморфная поверхность V ₃ всегда несет сеть линий кривизны. Отнесем ее к этой сети, т.е. b 2₃ = 0 . Если Я = 0 , то b 51 = 0 и вектор J ₄ принадлежит плоскости главной нормали и является вектором первой главной нормали кривой # '. Тогда главная нормаль N ₂ ( X ) является 1-голоморфной 2-плоскостью. В этом случае репер R является каноническим.

Заключение

Рассмотрены вещественные поверхности в евклидовом пространстве над алгеброй двойных чисел. Получены некоторые классы и найден в каждом случае произвол существования.