Виброакустическая модель прямолинейного неоднородного трубопровода при его силовом возбуждении пульсациями рабочей жидкости

Институт акустики машин, г. Самара

Представлена математическая модель поперечных вибраций прямолинейного неоднородного участка трубопровода при его силовом возбуждении пульсациями давления и скорости рабочей жидкости. Определены общие подходы к решению дифференциального уравнения четвертого порядка в частных производных с переменными коэффициентами, лежащего в основе модели. Представлены пути развития исследований.

Известно, что пульсации давления рабочей среды генерируют интенсивные поперечные колебания трубопроводов [1, 2, 3]. Данное обстоятельство приводит к существенному снижению их прочности и надежности. В настоящее время имеются многочисленные экспериментальные результаты исследования взаимодействия динамических процессов в рабочей жидкости с элементами гидромеханических систем. Например, в работах [3,4, 5] представлены экспериментальные результаты силового возбуждения трубопроводов пульсациями рабочей среды. Несмотря на большую практическую значимость решения задачи расчета амплитуд установившихся колебаний трубопровода под действием пульсирующего потока рабочей жидкости, она еще решена не полностью. В работе [6] предложено решение указанной задачи для частного случая основного параметрического резонанса. В работе [7] предложена виб-роакустическая модель прямолинейного однородного трубопровода. В ней решение уравнений, описывающих колебания трубопровода, осуществляется аналитическим путем. Сложность математических преобразований приводит к необходимости принятия допущений, оказывающих существенное влияние на точность решения задачи. В то же время в работе [8] отмечаются преимущества численного подхода к решению подобных уравнений.

В настоящей работе представлена математическая модель поперечных колебаний прямолинейного неоднородного участка тру бопровода в условиях пульсаций давления и скорости протекающей жидкости.

В отличие от предыдущих работ здесь учитываются:

• -    возможная неоднородность физических и геометрических параметров трубопровода вдоль его оси;

• -    число и упруго-жесткостные характеристики опор трубопровода;

• -    распределенность параметров пульсирующей жидкости.

Перечислим ряд принимаемых допущений:

• 1.    Изменением плотности жидкости пренебрегаем ( р _ж = const).

• 2.    Поперечные колебания системы не вызывают в жидкости никаких дополнительных волновых явлений.

• 3.    Известны демпфирующие свойства опор и материала трубопроводной системы, трением о воздух пренебрегаем.

• 4.    Жесткость сечения трубопровода на изгиб вдоль продольной оси является функцией, не имеющей разрывов второго рода.

• 5.    Кинематическое возбуждение трубопровода отсутствует.

Кроме перечисленных остаются в силе все обычные допущения сопромата.

При такой постановке задачи динамические свойства и характеристики источника пульсаций рабочей жидкости и присоединенной гидравлической цепи определяют краевые и граничные условия.

При изгибных колебаниях трубопровода круглого сечения в плоскости его оси эффекты, типичные для тонкостенных стерж-

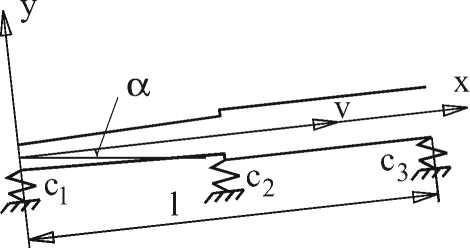
Рис. 1. Расчетная схема трубопровода

ней, не сказываются, ибо центр изгиба все

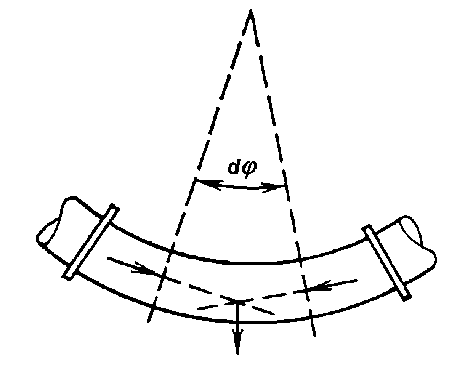
Рис. 2. Схема поперечных вибраций трубопровода

гда совпадает с центром тяжести сечения. Поэтому неоднородный прямолинейный трубопровод можно рассматривать как обычную балку с переменными по длине параметрами (рис.1). С учетом предположения 4 уравнение прогибов оси у имеет вид:

трубопровод жидкости

^^^^^^^^

тж

d ² у

dt

на

д4 у д2 M

^EI Х.4     2L.2 ’

где Е(х) - модуль упругости;

1(х) - момент инерции сечения относительно нейтральной оси;

у - прогиб трубопровода.

Изгибающий момент М в данном случае

выражается так:

M = M₀-Ny.             (2)

Здесь M 0 - изгибающий момент, который был бы при отсутствии продольной сжимающей силы N. Эта сила изменяется вдоль оси трубопровода за счет гидравлического трения и, если трубопровод не горизонтален, за счет составляющей веса оболочки по оси. Исходя из (2)

д ² M = _р _ N д ² у _ 2 д N ду _ д V дх ²          дх ² дх дх    дх ²

грузки, вызванной внутренним давлением.

Последняя определяется на основании рис.2. Если система прогнулась, то при бесконечно малом расстоянии между сечениями 1 и 2 поперечная сила, вызываемая внутренним давлением р, будет равна S_ж(x)pd^, где d ф - угол между сечениями 1 и 2. Значение этой силы на единицу длины есть S_ж(x)pd^/dx = - S_ж(x)pд ²у/дх². Здесь d^/dx= -д ²у/дх² есть кривизна оси.

Необходимо подчеркнуть, что траектория вектора средней по сечению скорости течения жидкости н(х, t ) не совпадает с изогнутой осью системы, поэтому сила инерции жидкости выражается через d²y/dt², а не через д ²y/dt², как сила инерции оболочки. Используя правила дифференцирования сложных функций, можно записать:

d ² у   d (ду    ду )   д ² у  (ди    ди ^ ду

-=1 — + и— =-^ + 1 -+ и - — + dt ²     dt I дt     дх 1    дt ²    I дt     дх I дх

Нормальная к оси системы нагрузка на

единицу длины

Р= д 2 M0

^P . 2

д ² у    2

+ 2и    + и дxдt

д¹ у дх ² ’

слагается из нор

мальной к оси трубопровода составляющей веса оболочки и заполняющей ее жидкости ( т_м ( х ) + т_ж ( х )) g, силы инерции оболочки

д ² У - т,, (х)—— ^{мV 7}д ²

, силы инерции заполняющей

где u(x,t) - средняя по сечению скорость течения.

Выражения для продольной сжимающей силы и ее частных производных по координате x запишем следующим образом:

N = N 0 + ^ок^ С Р ^ж8 и ² ( х, t ) х + т м ( х ) дх sin а,

XN   2LoKp (x)pжg /   \Xu(x, t)      / \.

— =-----2----и (х, t)—---+ т* (х )g sin а, ох       C

X ² N _^2L_0Kp ^{(х ) р} ж ^g f Xu ( x , t ) ^ ²     ,   хд ² u ( x , t )

x, = с2        . x- J + u(x-':

a i ^{( x} , t ) = E ( _x ) I ( _x ) ^[ m " ( x ^{) u 2 ( x} , t ^{) +}

+ S ( x ^ж

-

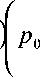
^{1    2 u} 0 ^{( x} )

P ж g V ^{C 2} r ( x )

)

- sin a x +

J

P = P o

1 ^{f 2u 2 ( x} ) P ж g V ^{C 2}r ⁽ x )

)

- sin a x + P ( x, t )

J

где N₀ - значение N при x = 0;

p₀ - стационарная составляющая давления при x = 0;

P(x,t) - пульсационная составляющая давления;

• р - плотность рабочей жидкости;

• g - ускорение свободного падения;

• а - угол наклона оси системы к горизонту ( а > 0 для нисходящих и а < 0 для восходящих трубопроводов);

L - длина контакта жидкости с окружающей ее оболочкой в плоскости поперечного сечения;

• u - скорость течения жидкости;

C - коэффициент Шези. Используя классическую формулу Маннинга, можно представить коэффициент Шези в виде [9]:

⁺     ' ^{)) + N} 0 ⁺ u ² ‘ > ⁺

+ m * ( x ) gx sin a ] ;

^a 2

a ₃

^2т ж ^{( x}) „г а ' E ( x ) I ( x ) ^{u ( x} ,t ^{) ;}

^m * ^{( x ) + т} ж ^{( x} ) _ E ( x ) l ( x ) ^;

a ₄ ( x, t ) =

+ u ( x, t )

E ( x ) I ( x ) _

/ / X u ( x, t ) ^тж ( x ) —/ +

" 1 X t

^X u ( x, _L > 4+ 2

X x

f 2L_0K ( x ) p g

I        икр \ /1 ^^

² V _xX u ( x,t ) X x

C2

u ( x, t ) x

⁺ m * ^{( x} ) g^{sin a}  ;

*

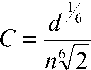
a ₅ ( x, t ) =

^2LOK_P ^{( x ) p}ж ^g f X u ( x, t ) J ²

C 2 EI    I  X x

+

n - коэффициент шероховатости (n=0,02_0,04);

d - внутренний диаметр трубопровода.

При дифференцировании учитывалось предположение 4, которое распространяется ^и на ^фун^кц^ии L_oK p =f_I ^(x ), m=f₂ ⁽ x).

X ² M

Подставляя в (3) значения 2 , T и N, Xx приходим к следующему уравнению поперечных колебаний:

л4-.,               л2.,л

—т- + ax (x, t)—, + a2 (x, t)

X x^{4     1V} ’ dx^{2     2V} ’ ^}xxdt

( \X² y . ( ^Xy ,

+ a3(x L;- + a4(x, t)   +(4)

Xt

+ a5 (x, t )y = аз (x )g, в котором обозначено:

+ u(x, tfPu^y- ' .

X x

Уравнение (4) описывает поперечные колебания неоднородного прямолинейного участка трубопровода с учетом движущейся с пульсирующим давлением жидкости. Уравнение (4) имеет структуру, схожую со структурой уравнения, полученного Н.С. Кондрашевым [6]. Некоторые отличия связаны с тем, что при выводе уравнения (4), в отличие от уравнения Н.С. Кондрашева, учитывались:

• -    изменение скорости жидкости по длине трубопровода и во времени;

• -    трение в жидкости;

• -    угол наклона оси трубопровода к горизонту;

• -    распределение пульсаций давления по длине трубопровода;

• -    изменение геометрических и физических

параметров трубопровода по длине.

Учет перечисленных факторов позволяет описывать уравнением (4) не только установившиеся периодические процессы в гидромеханической системе, но и моделировать поведение трубопровода во время переходных процессов в гидролинии.

Переходя к решению уравнения (4), несколько упростим его, приняв некоторые допущения, характерные для рассматриваемого случая установившихся периодических процессов в гидравлических линиях энергетических установок. Будем рассматривать горизонтальный участок системы (принимаем а 0). Пренебрежем потерями среднего давления по длине линии. С учетом этих допущений уравнение (4) можно переписать в виде:

34               ^2^2

"УТ + «ю (x, t)+ G20 (x, t) —£ + ox           oxoxot

( 3d2y ixdy

+ «30(x)v + «40(x, t L + dtox

⁺ « 50 ^{( x} , t ⁾ У ^- « 30 ^{( x} ) g = ⁰

где aM (x,t )=

E ( x1I ( x , ^[ m ж ^{( x}V ^{( x,t )+} S ж ^{( x} X P o ⁺

+ P(x,t))+ No + LOKP(x)pжg u2 (x,t)x a 20 (x,t ) =

^2m ж ^{( x )} E ( x ) l ( x )

u ( x,t ) ■

a 30 ^{( x )} =