Video Watermarking – Combination of Discrete Wavelet & Cosine Transform to Achieve Extra Robustness

Digital Watermarking is the technique of embedding a secret message or digital logo behind a cover medium. Cover medium can be image, text, audio or video and message can be image, audio or text. Digital watermarking is having its application in the areas of copyright protection and the authentication. In this era of internet and online transfer of the data, use of video watermarking is rapidly increasing because of the factors [1] explained below.

• •    Privacy of the digital data is required and because the copying of a video is comparatively very easy.

• •    Fighting against the “Intellectual property rights breach”

• •    Tempering of the digital video must be concealed.

• •    Copyright protection must not be eroded.

This paper focuses on the frequency characteristics of the 2-D data and makes use of two of the most prominent transforms applied on the 2-D images, namely Discrete Cosine Transform and the Discrete Wavelet Transform. In this paper we first converted video into the sequence of frames. The second step is to convert the RGB frame into its YCbCr version and then we made use of Y frame for the purpose of watermarking. This paper is organized in seven sections. Subsequent section explains the transform domain watermarking method. Section 3 and 4 explains the fundamentals of DCT and DWT. Section 5 shows the visual quality metrics used for evaluation purpose. Section 6 explains the proposed method and section 7 gives the results of proposed method.

• II.    T ransform domain watermarking

Embedding watermark into the video can be done in two ways namely spatial domain and transform domain [2]. In the spatial domain frame pixel values are modified according to the pixel values of the message to be hidden behind the frame where as in the transform domain frame pixel values are changed in the frequency domain according to the pixel values of the message. Transform domain watermarking makes use of various transforms like Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT), Discrete Cosine Transform (DCT) and other. Out of these transforms DCT and DWT are the most frequently used transforms because of their enormous capacity to break the image data into various frequency bands. According to priorities of the human visual system, we can choose one of the frequency bands to be used for embedding purpose. Figure 1 shows the idea of transform domain processing of the image data.

• III.    D iscrete C osine T ransform

Discrete cosine transformation [3, 4, 5, 6] (DCT) transforms a signal from the spatial into the frequency domain by using the cosine waveform. DCT concentrates the information energy in the bands with low frequency, and therefore shows its popularity in digital watermarking techniques. The DCT allows a frame to be broken up into different frequency bands, making it much easier to embed watermarking information into the middle frequency bands of a frame. The middle frequency bands are chosen such that they have minimize to avoid the most visual important parts of the frame (low frequencies) without over-exposing themselves to removal through compression and noise attacks (high frequencies).

Two dimensional DCT of a frame with size MxN and its inverse DCT (IDCT) are defined in Equations 1 and 2, respectively.

F ( и ,v)=

a ⁽ и ⁾ a ⁽v^{)∑     ∑     (} x , У ) соѕ [ ^{( г}т_ь ) ∙ ] соѕ [ ^{( 2У}" ^{) ∙} ]        (1)

Where а ( и )=√1/ М  for u=0;

а ( и )=√2/ М  for u=1,2,3,…..M-1;

а (v)=√1/ N   for v=0;

а (v)=√2/ N   for v=1,2,3,…..N-1;

/( X , У )=

^{∑    ∑} V» « ⁽ и ⁾ а ⁽v⁾ F ⁽ и ,V ) соѕ [ ^{( 2}Ть ) ∙ ] соѕ [ ^{( 2}Z ^{) ∙} ]       (2)

Where x = 0,1,2,……..M-1, y = 0,1,2,……..N-1

Figure 3(a) shows the three regions in the frequency domain. F L is used to denote the lowest frequency components of the block, while F H is used to denote the higher frequency components. F M is chosen as the embedding region as to provide additional resistance to lossy compression techniques, while avoiding significant modification of the cover video.

Fl	Fl	Fl	Fm	Fm	Fm	Fm	Fh	16	11	10	26	24	40	51	61
Fl	Fl	Fm	Fm	Fm	Fm	Fh	Fh	12		14			55	60	55
Fl	Fm	Fm	Fm	Fm	Fh	Fh	Fh	14	13	16	24	40	57	69	56
Fm	Fm	Fm	Fm	Fh	Fh	Fh	Fh	14		22	29	51	87	80	62
Fm	Fm	Fm	Fh	Fh	Fh	Fh	Fh	ie	22	37		68	109	103
Fm	Fm	Fh	Fh	Fh	Fh	Fh	Fh	24	35	55	64	81	104	113	92
Fm	Fh	Fh	Fh	Fh	Fh	Fh	Fh	49	64	76	67	103	121	120	101
Fh	Fh	Fh	Fh	Fh	Fh	Fh	Fh	72	92	95	98	112	100	103	99

(a)

(b)

Figure 2. Defination of DCT regiouns and Quantization values used in JPEG compression scheme[6]

• IV.    D iscrete W avelet T ransform

The Basic Idea of the Discrete Wavelet Transform [7, 8, and 9] may be understood by taking a one dimensional signal which is first split into two parts, usually high frequencies and low frequencies [10]. Again the low frequency part is divided into two frequency components of high and low frequencies. This process is continued until the signal has been entirely decomposed. Furthermore, from the DWT coefficients, the original signal can be reconstructed. The reconstruction process is called the inverse DWT (IDWT). The idea of the DWT is as shown in the figure 3.

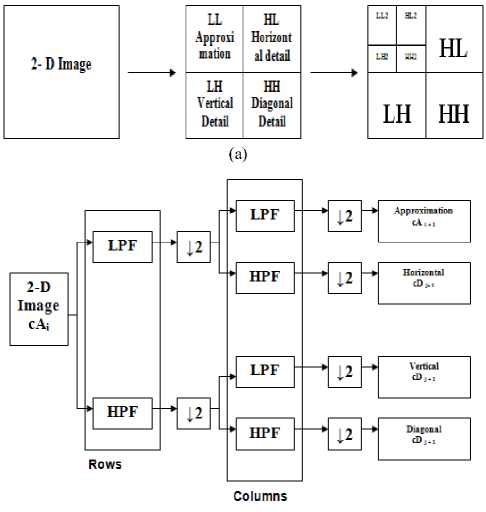
(b)

Figure 3. Basic decomposition steps for images

• V.    V isual quality M atrices

We have mainly used the following visual quality matrices [14] for the sake of comparison of degradation after the watermark is added to video.

MSE=мIN^∑xtl ^∑у=1{(f(x, y)-f (x, y))^2}            (3)

PSNR=10×log                                 (4)

Here MSE – Mean Square Error

PSNR – Peak Signal to noise Ratio

f(x,y) – Original Frame of the video f’(x,y) – Watermarked Frame of the Video.

The phrase peak signal-to-noise ratio [14], often abbreviated PSNR, is used to measure the similarity between two signals where in one is original and the other is altered version of the same. PSNR can be defined via the Mean Square Error (MSE) which gives us the idea of difference between the original and the altered signal. PSNR is measured in the logarithmic scale and MSE is measured in the general scale.

At the receiver end we extracted the watermark and measured the correlation [14] of the recovered watermark and original watermark for the sake of checking the robustness.

• VI.    P roposed A lgorithm

In our proposed method qualities of both the DWT and DCT are used for the purpose of embedding. Figure 4 shows the diagram of the proposed method. In this we made use of the combined DWT-DCT for the purpose of watermarking. Some of the glimpses of the proposed method are:

• 1.    Rather than inserting the watermark into the DCT coefficients directly, we first apply a 2-level DWT to have seven sub-bands.

• 2.    We choose horizontal sub-band and then apply DCT to have DCT coefficients and then we modify the mid frequency coefficients.

• 3.    Here robustness is improved by the ability of the DWT to increase the energy of the watermark which makes use of the properties of the HVS.

• 4.    Furthermore imperceptibility is also achieved by the DWT.

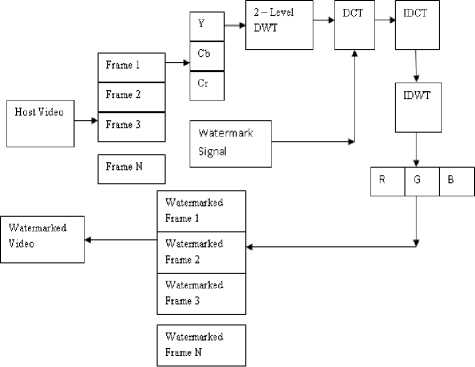
Figure 4.Block Diagram of the proposed scheme

(a)

Message: 1 KITA ano	Message:2 KITA ano
M e s s a g e: 3	Messagez4
шта	RITA
Я1Ю	Я11О

(b)

• 1.    Luminance component carries the major information of the frame and is perceptibly most important to the Human eye as compare to the color information.

• 2.    While frame undergoes JPEG compression color components are down-sampled but luminance samples are kept as it is.

Therefore choosing Y frame is better so far as perceptibility and robustness of the watermarking is concerned. Following are the expressions conversion from RGB to YCbCr and vice-versa [13].

Y = 16 + 65.481*R + 128.553*G + 24.966*B(5)

Cb = 128 – 37.797*R – 74.203*G + 112*B(6)

Cr = 128 + 112*R – 93.786*G – 18.214*B(7)

R = Y  + 0 * Cb + 1.402 * Cr(8)

G = Y - 0.344136 * Cb - 0.714136 * Cr(9)

B = Y  + 1.772 * Cb + 0 *Cr(10)

• A.  E MBEDDING A LGORITHM

Following is the stepwise representation of what we have done for the video watermarking using the proposed algorithm.

• 1.    Video is converted into the sequence of frames.

• 2.    Color space conversion is done from RGB to YCbCr.

• 3.    A two-level DWT is performed and HH2 band is selected for the further process.

• 4.    Block based DCT is applied onto the HH2 band and middle band frequency coefficients are modified in accordance to the binary watermark.

• 5.    Inverse DCT is performed to get the watermarked HH2 band.

• 6.    Inverse DWT is performed two times so as to get watermarked Y frame.

• 7.    Reverse color space conversion from YCBCr to RGB is performed so as to get watermarked RGB frame.

• 8.    Steps 2 to 7 are repeated until all the frames are not completed.

• 9.    All watermarked RGB frames are combined to get watermarked RGB video.

• 4.    Block based DCT is applied onto the HH2 band and middle band frequency coefficients are modified so as to get the binary watermark.

• 5.    Steps 2 to 4 are repeated until all the frames are not completed.

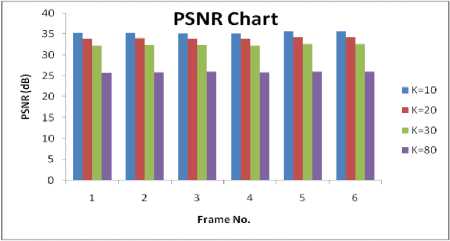
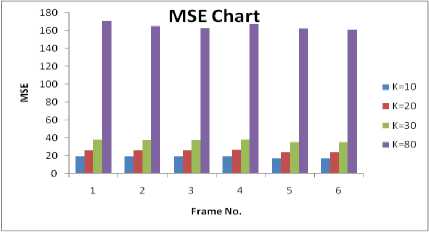
  Figure 8 shows the watermark extracted from the first six frames for k=10 and k=80 and figure 9 shows the comparative chart of correlation for various values of k.

  
  
  

Figure 6 shows the first six of the frames for the value of gain factor k=80 and figure 7 shows graphical representation of the results that we get.

Figure 5. (a) First Four Frames of the Video (b) Messages to be embedded behind each frame

Figure 6. Watermarked Frames

Figure 7 shows the PSNR and MSE results for the various values of the gain factor k. One can observe that as the value of k increases the difference between the original and the watermark frame increases and therefore an increased MSE and reduced PSNR is obtained.

(a)

(b)

Figure 7. (a) Peak Signal to Noise Ratio Chart (b) Mean Square Error chart

• B.  E XTRACTION A LGORITHM

We followed following steps to obtain the message back from the watermarked video sequence.

• 1.    Video is converted into the sequence of frames.

• 2.    Color space conversion is done from RGB to YCbCr.

• 3.    A two-level DWT is performed and HH2 band is selected for the further process.

Figure 8.Watermarks extracted wih K = 80

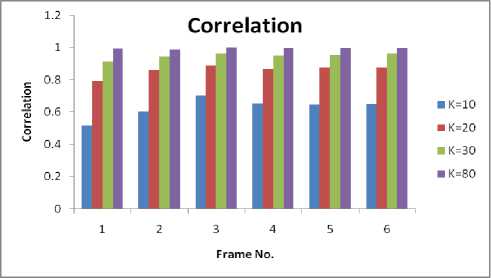
Figure 9.Correlation Chart

We can observe that as the value of k increases, the perceptibility of the recovered watermark and hence the correlation of the same with the original watermark increases.

Table 1 shows the results of PSNR, MSE and Correlation with various values of Gain Factor.

TABLE 1. PSNR, MSE AND CORRELATION RESULTS WITH VARIOUS ALPHA

Gain Factor	PSNR-dB	MSE	Correlation
10	48.6013	0.8973	0.0735
20	48.5689	0.904	0.1519
30	48.5249	0.9133	0.2145
40	48.4477	0.9296	0.2617
50	48.3693	0.9466	0.3195
60	48.263	0.97	0.36
70	48.1445	0.9969	0.3976
80	48.024	1.0249	0.4264
90	47.8987	1.0549	0.4629
100	47.7528	1.0909	0.4832

• VII. R obustness R esults

We applied various attacks to the watermarked frame and got some of the results that are explained as under. Here we used another watermark to check the robustness.

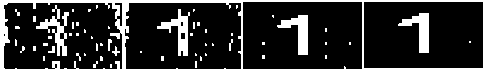
(a)                (b)                (c)

(d)

Figure 10.Recovered Watermarks after compression (a) 65% (b) 45% (c) 25% (d) 5%

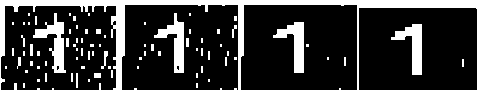
(a)

(b)                (c)              (d)

Figure 11.Recovered Watermarks after Gaussian LPF of with mask size 21 x 21 and sigma of (a) 1.3 (b) 1 (c) 0.7 (d) 0.4

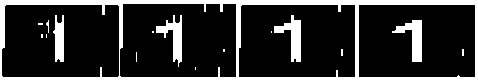
(a)                  (b)                (c)             (d)

Figure 12.Recovered Watermarks after approximating linear motion of camera with motion pixels (a) 50 (b) 35 (c) 20 (d) 5

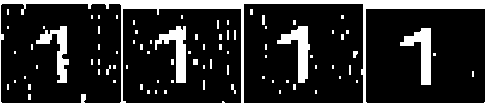
(a)                  (b)                (c)               (d)

Figure 13.Recovered Watermarks after added Gaussian with 0 mean and variance of (a) 0.009 (b) 0.007 (c) 0.005 (d) 0.001

Table 2 shows the results under various attacks.

TABLE 2. PSNR, MSE AND CORRELATION RESULTS UNDER VARIOUS ATTACKS

		Correlati on	PSNR	MSE
Averag e Filterin g	3	-0.0205	36.3353	15.1201
	5	0.027	33.5018	29.0339
	7	0.0374	32.0972	40.12
	9	0.0201	31.2022	49.3017
	11	-0.0082	30.5701	57.0257
	13	0.0244	30.0968	63.5916
	15	0.0263	29.723	69.3073
Compr ession	5	-0.0369	30.7373	54.8726
	10	0.0126	33.0748	32.0329
	20	0.0069	36.8717	13.3631
	40	-0.0166	39.558	7.1992
	60	-0.0139	41.229	4.8999

	80	-0.0259	43.3279	3.022
	95	0.0067	43.5051	2.9012
Linear Motion of the Camera	5	0.0561	35.2706	19.3205
	10	0.063	32.3212	38.1033
	15	0.0641	31.0839	50.6633
	20	0.0667	30.3327	60.2291
	25	0.0745	29.807	67.9793
	30	0.064	29.4072	74.5354
	35	0.0564	29.1015	79.9712
Gaussia n Noise with 0 Mean and Variabl e Varianc es	0.0005	0.0505	36.0944	15.9822
	0.005	0.0584	29.9163	66.2902
	0.01	-0.0092	29.103	79.9438
	0.09	-0.0023	27.9542	104.1513
	0.4	0.0311	27.6725	111.1289
	0.8	-0.0002	27.5918	113.2131
	1	-0.0214	27.5939	113.1582
Gaussia n Noise with Variabl e Mean 0.0005 Varianc e	0.0005	0.0699	36.0942	15.9831
	0.005	0.0553	39.2516	7.7255
	0.01	0.0366	56.8664	0.1338
	0.09	0.0469	80.5809	0.0006
	0.4	0.0359	84.4423	0
	0.8	-0.0063	90.1024	0
	1	0.0192	99.1159	0
Color Reducti on	4	0.0109	28.9155	83.4694
	8	0.04	29.77	68.561
	16	-0.0174	31.1096	50.3646
	32	0.0212	32.5424	36.2106
GLPF with Sigma Values	0	0.99694	34.4929	23.1101
	1	0.73087	30.2367	61.599
	1.5	0.15054	29.4309	74.1606

VIII. C onclusion

From the work carried out, we concluded that as we increase the value of the gain factor the perceptibility reduces but watermark strength increases and we can recover a better watermark at the receiver end. We also observed a good robustness against the compression, filtering and noise attacks.