Viewpoint Selection Using Hybrid Simplex Search and Particle Swarm Optimization for Volume Rendering

Published Online September 2012 in MECS

Volume rendering has become an important volume visualization technique, since it can reveal the overall structural information in volume data. However, low efficiency and inconvenient interaction caused by a great deal of complicated data processing has limited its widespread use. Therefore, it has been the focus in current study how to optimize the approach of volume rendering by utilizing intelligent technique. One of the feasible schemes is to locate the globally optimal viewpoint or a set of the optimized viewpoints for volume rendering by intelligent algorithm. The research in this area is generally ascribed to viewpoint selection. At present, the study of viewpoints selection is summarized as follow two aspects: one is viewpoint quality evaluation; the other is the intelligent method of viewpoint selection.

In the viewpoint quality evaluation, the information-theoretic entropy is usually adopted to express the amount of visual information presented in a view. The basic idea is that the higher the entropy of a viewpoint is, the more abundant information in volume data can be observed, thus the better quality of the viewpoint will be. We can therefore evaluate the quality of a viewpoint by means of comparing the entropy value of threedimensional image at different viewpoints. Currently, there are two common approaches for establishing the viewpoint entropy function. One approach is defining viewpoint entropy function in iso-surfaces, gradient directions[1] or a set of feature components[2] by extracting structural features from volume dataset; the other approach is directly defining the viewpoint entropy function at voxels by regarding voxel’s opacity as a significant element to describe visual information in volume data[3,4].

In the intelligent method of viewpoint selection, the search for the optimal viewpoint is transformed as an optimization problem, in which the intelligent technique is used to optimize its procedure for the improvement of its efficiency and automatic level. In actuality, only a few intelligent methods have been applied in this area until now, such as the particle swarm optimization (PSO)[5] etc.

This paper proposes an intelligent method of viewpoint selection based on the hybrid Nelder-Mead (NM) simplex search and PSO algorithm (NM-PSO) . It constructs the viewpoint quality evaluation function based on information entropy by integrating luminance and structural features in two-dimensional projective image of volume data. In the process of viewpoint selection, every particle in the hybrid NM-PSO algorithm is encoded as a potential candidate viewpoint and its fitness function is replaced by the viewpoint evaluation function. PSO algorithm focuses on exploration of global optimum and NM simplex search focuses on further local exploitation of the current optimum. The viewpoint is finally optimized in sequential iterations. Experimental results show that this method combines the advantages of global optimizing in PSO and local efficient searching in NM-simplex. The procedure is highly effective at locating the optimal viewpoint. The optimized viewpoints can reveal the important structures or the region of interest in volume data.

The remainder of this paper is organized as follows: Section 2 defines the formula called the viewpoint entropy function and validates its availability to evaluate the viewpoint quality through the three-dimensional reconstructed experiments of human head CT data. In Section 3, after briefly introducing NM simplex search algorithm and PSO algorithm, the procedure of the hybrid NM-PSO algorithm is described in detail. Section 4 shows our method, which uses the hybrid NM-PSO algorithm for optimal viewpoint selection. Section 5 presents some experimental results and analysis. Finally, major conclusions of this paper are summarized in Section 6 along with some remark of areas of future research.

II. Viewpoint Quality Evaluation Based on Information Entropy

Entropy is an information-theoretic concept about information amount measurement. Suppose an information source X randomly produces a series of signals x i ( i =1,2,...,m) and the probability of x i appearing in the series is p ( x i ), thus the entropy of information source X may be defined as:

m

^{H (} X) = - E P ⁽ xi )log 2 P ⁽ x i )                  (1)

i = 1

Where V ( k )=[ α ( k ), β ( k )] denotes the directional vector of viewpoint k . α ( k ) ∈ [0^o, 360 ^o] is the angle between the projective vector of V ( k ) on XZ plane and X coordinate axis. β ( k ) ∈ [0^o, 180^o] is the angle between V ( k ) and Y coordinate axis. M is the total number of pixels in two-dimensional projected image that is orthogonal with V ( k ). I i , w Ii respectively represent luminance and normalized structure information factor of the pixel i . In the boundary regions, w Ii approaches 1, while approaches 0 in the smooth regions. Since the structural information generally concentrate on image edge, the structure information factors may obtain by extracting edges in two-dimensional projective image. Typical edge detecting arithmetic operators include Roberts, Prewitt, Sobel and Canny etc.

To illustrate the availability of viewpoint entropy, Figure 1 shows the experimental results about human head CT dataset(256×256×256) which is rendered by using three-dimensional texture mapping^[6]. Here suppose volume dataset is centered at coordinate origin and the viewpoint k lies on the view region sphere whose center is at the origin. Vector V ( k ) points from the origin to viewpoint k . In the experiments, the viewpoint revolves 360^o in horizontal direction around three-dimensional reconstructed image, and the viewpoint quality is evaluated at 1° increments. Figure 1(a) shows the change curve of viewpoint entropy as the viewpoint revolves in horizontal direction at 1° increments. Figure 1(b)-(e) respectively show the twodimensional projective images which are obtained at 12°, 112°, 158° and 270° in horizontal direction. Figure 1(b) and (d) are the best and the worst view, their entropy values reach the maximum 10.16 and the minimum 9.72.

When the signals produced from information source X have the highest incertitude, that means p ( x 1 )= p ( x 2 )=…= p ( x m )=1/m, information amount in source X will be highest and entropy will reach maximum log 2 m.

Since the transfer function of volume rendering generally assigns important voxels higher luminance, voxel’s luminance may be one of variables of entropy function. Moreover, the structural information factor should also be considered in entropy function to represent structural features in volume data. Because it is two-dimensional projective image of volume data finally to display on screen in volume rendering, we may design the entropy function on the two-dimensional projective plane in order to reduce complicated analysis and calculation in volume space. Equation (2) is the viewpoint entropy function by using the luminance and structural feature of two-dimensional projective image.

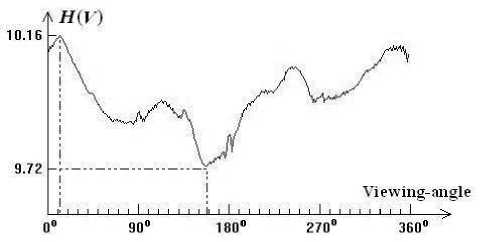
(a) The change curve of entropy with horizontal viewing angle

M - 1

H [V (k)] = -£ i=0

wl. • I, M-1/         \

£ ( wij- Ij)

j = 0

• log

w n • Ii

M-1/         \

E⁽ wij- Ij)

j = 0

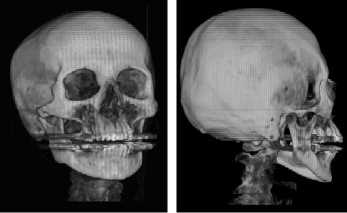
(b) 12°                  (c) 112

⁰ ^ w ii , w ij ^ ¹

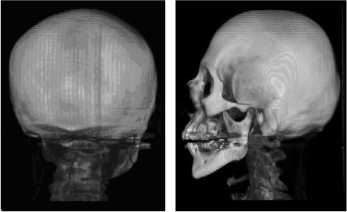
(d) 158°               (e) 270°

Figure 1. Viewpoint evaluation experiment of CT dataset of human head

Pc = PPmn + (1 — в) Pcent-             (5)

Where 0< P <1 is the contraction coefficient. If Pc function value fc≥fmin, the contraction has succeeded and let Pmin=Pc, then return to step 2); or else the contraction has failed and will still need to shrink all simplex vertices except Pmax in (6), then return to step 2) to start a new iteration.

Pi = 5Pi+ (1 - 5) P„x , Pi* P.„     (6)

Where 0< 5 <1 is the shrinkage coefficient.

III. The Hybrid NM-PSO

A. Nelder-Mead Simplex Search Algorithm

The Nelder-Mead Simplex Search is a classical local direct search algorithm for unconstrained optimization[7], which constructs a simplex with N+1 vertices in N-dimensional space and continually rescales it to gradually converge to the optimal solution of the function by using three basic operations: reflection, expansion and contraction. The procedure is outlined below:

B. PSO Algorithm

The PSO is one of the intelligent algorithms based on colony evolution[8]. In the procedure of PSO, a swarm of particles with variable velocities are randomly distributed in the search space to represent as potential solutions about optimization problem. According to the particle’s previous best location and the current global best location, these particles continually update their locations to get closer to the global optimum. The updating equations of particle swarm are given as follows:

• 1)    Initialization: For the maximization of N-dimensional function f, Create N+1 vertices expressed as the vectors, to construct an initial N-dimensional simplex. Calculate the function values of all vertices.

• 2)    Reflection: Determine Pmin, Psmin, Pmax vertices respectively corresponding to the minimum fmin, second minimum fsmin and the maximum fmax of function f. In the opposite direction of Pmin, produce a reflection vector Pr in (3), which function value f is equal to fr:

n + ¹ v kd

= wvnd+c1 r1[ pnkd- xnd]

⁺ c 2 r 2 ^[ P ^d — x kd ^]

<

'P r = (1 + a ) P cent - a>

1 N + 1

¹ cent                   i , i ' mix

^           N i = 1

Where a >0 is the reflection coefficient. If f _min ≤ f r ≤ f max , then accept the reflection and let P min = P r ， return to step 2); or else if f r > f max , go to expansion, if f r < f smin , go to contraction.

3) Expansion: In the reflection direction, find the expansion vector Pe in (4), which function value f is equal to fe:

x k+ = xkd + v Ы (8)

Where v kd is the flight speed of particle k in d dimension direction in the search space, that also is particles moving distance in unit time; p kb is previous best location of particle k ; p gd is the global best location of entire swarm in d dimension direction until now; r 1 , r 2 is random number between [0,1] in order to maintain the diversity of the population; w is an inertia weight. c 1 and c 2 are respectively the cognitive coefficient and social coefficient; x kd is the coordinates of the particle k in d dimension direction; n is the iterative times. In the optimizing process, each particle has a fitness function f ( x d ) denoting its optimized degree.

Pe = YP + (1 — Y) Pcent

Where γ>1 is the expansion coefficient. If fe >fmax, then accept the expansion and let Pmin=Pe; or else let Pmin=Pr, then return to step 2).

4) Contraction: If fmin< fr< fsmin, first let Pmin=Pr and then contract in (5); If fr < fmin, directly contract in (5):

• C. The Hybrid NM-PSO Algorithm

The hybrid NM-PSO algorithm combines the advantages of the local efficient searching of NM simplex and the global exploration of PSO, and so exhibits better performance of convergence rate and accuracy, global search ability and robustness[9]. The procedure of the hybrid NM-PSO algorithm is described below:

• 1)    Initialization for N-dimensional problem, randomly generate 3N+1 particles.

• 2)    Evaluation and ranking. Evaluate the fitness of each particle and rank them in term of the fitness values.

• 3)    Simplex search. Apply a NM simplex algorithm to the top N+1 particles with best fitness for further optimizing.

• 4)    PSO. Apply PSO algorithm for updating the rest 2N particles with worst fitness.

• 5)    Judgement. Judge whether termination criterion is reached. If reached, pick out the particle with global best fitness as the result; or else return to step 2).

• IV.    Viewpoint Selection Using The Hybrid NM-PSO Algorithm For Volume Rendering

In the viewpoint selection based on the hybrid NM-PSO algorithm, each particle is regarded as a possible viewpoint on view region sphere, so that the coordinates x k of particle k may be replaced by the direction vector V ( k )=[ α ( k ), β ( k )] of viewpoint k and its fitness function f ( x k ) also replaced by the viewpoint entropy function H [ V ( k )]= H [ x k ].

The procedure of viewpoint selection based on the hybrid NM-PSO algorithm is given as below:

• 1)    Initialization. Randomly generate a population of size 3N+1 and assign a random velocity to each particle. Set the related coefficients for the hybrid NM-PSO algorithm.

• 2)    Evaluation of viewpoint quality. Regard each particle as a potential candidate viewpoint. Calculate the entropy values of two-dimensional projective images at these potential viewpoints in (2) and act as the fitness of particle f( x k ) ＝ H[ x k ], k=1,2,…,3N+1.

• 3)    Ranking. Rank all particles in the light of their fitness values and record each particle’s best location and the current global best location of entire swarm.

• 4)    Simplex search. Construct a simplex by the top N+1 particles with highest fitness value and apply NM simplex algorithm to further optimize the locations of these particles in (3)-(6).

• 5)    PSO. Apply PSO algorithm to update the rest 2N particles with worst fitness values in (7), (8).

• 6)    Judgment. Judge whether termination criterion is reached. If reached, the algorithm end, output the coordinates xg of the particle with the global highest fitness value as the optimal viewpoint, or output a set of coordinates ｛ xk ｝ of the particles with higher fitness values as a series of important viewpoints {V(k)}; or else return to step 2).

• V.    Experimental Results And Analysis

To verify the performance of the proposed method in the viewpoint selection of volume rendering, we have experimented with several typical volume datasets and compared with the methods based on PSO or NM simplex algorithm. Since viewpoint selection may be considered as a four-dimensional optimization problem about viewpoint entropy function on view region sphere, we make the population sizes of above three algorithms all equal to 3N+1=13 (corresponding to N=4) in the experiments. In PSO algorithm, study coefficient c1 and c2 are both 2, and the inertia weight w linearly will descend from 0.8 to 0.4 as iterative times. In NM simplex search algorithm, the reflection coefficient α is 1, the contraction coefficient β and the shrinkage coefficient δ are both 0.5 and the expansion coefficient γ is 2.5[7]. The related coefficients in the hybrid NM-PSO algorithm are the same as the above algorithms. All 13 particles are separated into two groups in the every iteration of the hybrid NM-PSO algorithm: the top N+1=5 particles with highest fitness values are selected to take part in NM simplex search and the rest 2N=8 particles with worst fitness values are adjusted in PSO. In addition, the structure information factor wIi in viewpoint entropy function (1) is obtained by using the normalized Sobel operator to filter the two-dimensional projective image of volume rendering. All tests are run on 2.66GHz Intel Core i5 with NVIDA Quadro NVS3100M (512M) graphics card and 2GB RAM. The design software is Visual C++ 6.0 and OpenGL 2.0.

Figure 2 exhibits the viewpoint selection results in our method, including the CT scan of a human head, protein molecules and a bonsai tree, as well as X-ray scan of a human foot. Figure 3 shows the evolution curve of viewpoint entropy of the human head dataset. TABLE 1 shows the average convergence time of 10 runs of three different algorithms.

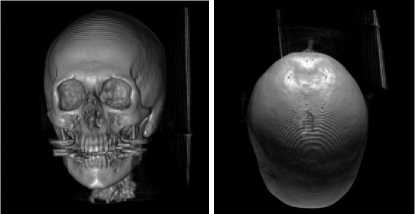
(a) The best and the worst viewpoint of human head

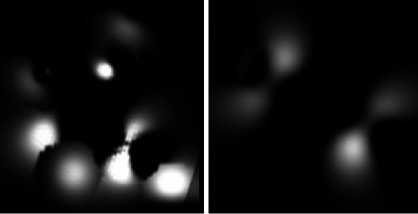
(b) The best and the worst viewpoint of protein molecules

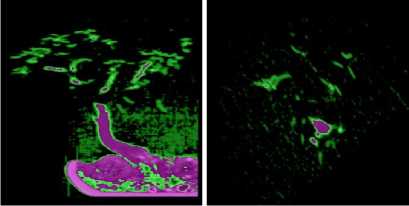
(c) The best and the worst viewpoint of bonsai tree

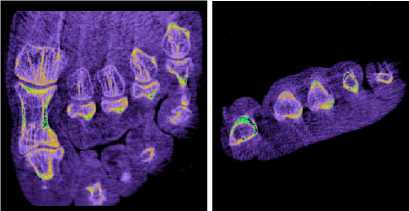
(d) The best and the worst viewpoint of human foot

Figure 2. The results of viewpoint selection using hybrid NM-PSO algorithm

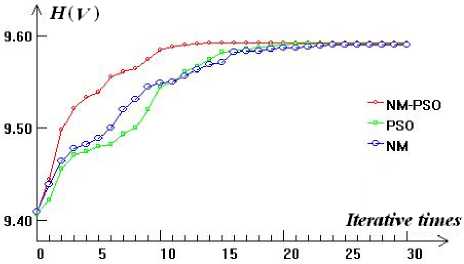
Figure 3. Evolutions of viewpoint entropy of human head of three different algorithms

TABLE 1. AVERAGE CONVERGENCE TIME OF 10 RUNS OF THREE DIFFERENT ALGORITHMS

Volume dataset	entropy	NM simplex	PSO	NM-PSO
head	9.57	11.847s	11.542s	9.934s
protein molecules	9.45	4.929s	4.793s	4.328s
bonsai tree	9.59	5.286s	5.275s	4.184s
foot	9.56	6.126s	6.053s	5.671s

From the experiment results above, some advantages of our method can be summarized as follow:

• 1)    The integrated ability of global optimization and local search. PSO algorithm is used for the most particles with lower entropy values to explore the optimal viewpoint on whole view region sphere, so as to ensure globally optimizing ability. On the other hand, NM simplex algorithm chooses the fewer particles with highest entropy values to further locally search for the higher viewpoint entropy value, thereby making the convergence rate and accuracy superior to pure PSO.

• 2)    The more effective convergence. Although the computational complexity of the hybrid NM-PSO algorithm increases relative to the other two algorithms in the every iteration, the time of searching optimal viewpoint oppositely decreases due to the algorithm itself high astringency. So the efficiency of viewpoint selection using the hybrid NM-PSO algorithm is higher than that using other two algorithms.

• 3)    The stronger robustness. The hybrid strategy of NM-PSO not only avoids premature convergence of PSO algorithm and sensitivity to the choice of initial points of NM simplex search, but also ensures that the search is less likely to be trapped in local optima that often arise from employing NM simplex local search algorithm. The results of viewpoint selection have the stronger robustness and reliability.

• 4)    Decrease the computational complexity of viewpoint evaluation. The viewpoint entropy function proposed in the paper is defined on twodimensional projective plane, thus avoids the complicated analysis of three-dimensional volume datasets.

• 5)    Our method for viewpoint quality evaluation accords with the structural sensitivity of human visual system. Besides the luminance representing voxel’s importance, the structural information factor is also introduced into entropy function to indicate structural features in volume data.

• VI. Conclusion

The complexity of volume data and the diversity of volume visualization lead to frequent man-machine interactions in volume rendering, so as to obviously reduce efficiency and flexibility. One of the feasible schemes for the improvement of the efficiency and flexibility is to utilize intelligent technique to guide and optimize the process of volume rendering.

From the viewpoint of global optimization problem, we formulate the criterion to evaluate viewpoint quality as information-theoretic entropy function of twodimensional projective image, and then apply the hybrid NM-PSO algorithm to locate optimal viewpoint or a set of optimized viewpoints for volume rendering. This approach has effectively reduced reduplicate interactions and improved the level of intelligent and automation of volume visualization. Our procedure is of special significance or value for non-interactive visualization of large datasets.

At the present time, there are two aspects worthy of notice in the study of viewpoint selection of volume rendering. One is the intelligent techniques related to viewpoint selection have still not investigated sufficiently and until now many excellent intelligent algorithms have not set foot in this field. So the further research is possessed of great potentialities and space.

Secondly, there exist the certain relations between viewpoint selection and transfer function of volume rendering. Therefore, how to synthesize both to optimize the process of volume rendering is an important problem worthy of deep study.

Acknowledgment

This paper is supported by the National Science Fund Program of China (No. 61075028).