Вихревой Фурье-инвариантный пучок Лагерра-Гаусса в квадрате

В настоящее время большое количество публикаций посвящено оптическим вихрям [1 –3], способам их формирования [4– 10] и широкому спектру прикладных задач, где они применяются [11 – 19]. Одно из важных направлений исследований – это поиск новых типов пучков, обладающих определенными свойствами [20–27]. Так, например, в работе [20] авторы предложили новый тип неканонического оптического вихря, названный «фазовым вихрем экспоненциального порядка», экспериментально продемонстрировали спиральную фокусировку автофокусирующих пучков Эйри, несущих данный вихрь, и теоретически проанализировали потоки энергии и орбитальный угловой момент. Новый класс источников, обладающих свойствами структурированной когерентности, полученный путём некогерентной суперпозиции когерентных мод Лагерра–Гаусса (ЛГ), предложен и исследован в [21]. В работе [22] авторами рассматривается векторный пучок Лиссажу (ВПЛ) двойного порядка ( p, q), поперечные компоненты которого имеют угловое соотношение, соответствующее кривым Лиссажу. В статье проведен теоретический и численный анализ ВПЛ, показавший, что соотношение и четность порядков ( p, q) влияют на свойства различных компонент электромагнитного поля. В [23] был предложен новый тип спиральноконического оптического пучка с экспоненциальной мощностью. Авторы теоретически и эксперименталь- но исследовали интенсивность таких пучков в фокусе и продемонстрировали их применимость для оптического захвата. В нашей работе [24] предложен новый вид пучков Бесселя, обладающих свойством Фурье-инвариантности и поэтому названных пучками Фурье–Бесселя. Данные пучки, в отличие от известных пучков Бесселя, имеют слабые боковые лепестки, а по сравнению с модами Лагерра–Гаусса с нулевым радиальным индексом – меньшее внутреннее темное пятно. При этом пучки Фурье–Бесселя обладают конечной энергией, хотя у них нет Гауссовой огибающей. В [27] рассматривается интересный вид пучков – «фотонные крючки», возникающие за счет дисперсии фазовой скорости волн внутри, например, составной частицы, и последующей интерференции. Такие пучки имеют самый маленький радиус кривизны фотонного луча из когда-либо зарегистрированных, который примерно в два раза меньше длины электромагнитной волны. В [28] нами были рассмотрены синусоидальные Гауссовы пучки с единичным топологическим зарядом. Этот пучок относится к типу элегантных лазерных пучков, так как и в начальной плоскости, и в зоне дифракции Френеля описывается одной и той же функцией с комплексным аргументом. Было показано, что диаметр первого светового кольца у синусоидального Гауссова пучка почти не зависит от радиуса перетяжки Гауссова пучка.

Несмотря на все вышеперечисленное обилие различных подходов для создания и описания новых ти- пов пучков, не теряют свою актуальность и хорошо всем известные пучки Лагерра–Гаусса [29–34]. В работах [29–31] рассмотрены различные варианты генерации данных мод с использованием специального лазера, использующего усиленную внутрирезонатор-ную сферическую аберрацию [29], q-пластинки [30] или специальной метаповерхности [31]. В работе [32] обсуждается взаимное преобразование между модами Эрмита–Гаусса (ЭГ) и модами ЛГ. Важное значение имеют исследования элегантных пучков ЛГ, демонстрирующих исключительные характеристики во многих областях, таких как оптическая связь и оптический захват. Так, например, в работе [34], авторы предложили метод измерения топологического заряда частично когерентного элегантного пучка ЛГ.

На базе мод ЛГ разрабатываются новые типы оптических пучков, обладающих различными полезными свойствами. Так, например, в одной из своих работ авторы этой статьи предложили семейство асимметричных лазерных пучков ЛГ [35], а в работе [36] другая научная группа представила метод генерации таких пучков высокой мощности. Авторы работы [37], используя моды ЛГ, продемонстрировали возможность генерации векторного пучка с пространственно-зависимой поляризацией в поперечном сечении посредством нелинейного магнитооптического вращения. Новый класс составных вихревых пучков, получаемый путем коаксиального наложения пучков ЛГ с одинаковыми параметрами (расстояние и радиус) перетяжки, был представлен в [38]. В [39] был теоретически и экспериментально исследован новый тип частично когерентного пучка с нетрадиционной корреляционной функцией, названной эллиптической коррелированной моделью Лагерр–Гаусса–Шелла (МЛГШ). Интенсивность таких пучков в дальнем поле (или в фокальной плоскости) имеет эллиптический кольцеобразный профиль. Стоит отметить, что пучки ЛГ и подобные им имеют высокую практическую значимость для оптических коммуникаций [40–42], микроманипулирования [43] и фотовозбуждения атомов [44].

В данной работе мы предложили новый тип оптических пучков, амплитуда которых пропорциональна многочлену Лагерра в квадрате. Эти пучки расширяют базис мод ЛГ. Было проведено их теоретическое и численное исследование, показана их Фурье-инвариантность.

1. Теоретическое основание

Рассмотрим пучок ЛГ, комплексная амплитуда которого в начальной плоскости ( z =0) имеет вид [45]:

„ , ,           ( r 2    . V r I ” ' ,I / r ² I     х

E n , m ( r , ф ) = E o exp l-— ■ in ф|| —I L i m ¹ 1 t I , (1) I 2 w ²     Д w )    ^ w ² )

где ( r , φ, z ) – цилиндрические координаты, w – радиус перетяжки Гауссова пучка, L ⁿ _m – обобщённый много-

член Лагерра ( n – целочисленный азимутальный индекс, а m ≥ 0 – целочисленный неотрицательный радиальный индекс). Так как пучок (1) является модовым пучком, то есть при распространении в свободном пространстве сохраняет свою структуру, то комплексная амплитуда пучка ЛГ на любой плоскости z описывается выражением, подобным (1):

г \ P w ( r2      ikr2

En,m(r,ф) = E0—-expl ——— + —— + inФ I w (z) ( 2 w 2( z) 2 R (z)

( r I n (f r 2 I xlttI Lm|        exp(i(in।+2m+1жz)),

(w (z)) (w 2( z)) x'

где

z2                 ( w (z) = w 1 + — , R (z) = z| 1 + —|, zz

'       ", (3)

t ( z I      kw2    _

c( z) = arctanl — |, z 0 =----, E 0 =

( z 0 )        2 \j n ( n + m )!

w ( z ) – радиус Гауссова пучка, R ( z ) – радиус кривизны волнового фронта Гауссова пучка, ξ ( z ) – фаза Гоу, z 0 – длина Рэлея, E 0 – нормировочная константа, k – волновое число света.

Рассмотрим теперь пучок, который мы назвали пучком ЛГ в квадрате (ЛГ)2 и комплексная амплитуда которого в начальной плоскости имеет вид:

E 2, n , m ( r , ф ) =

= E ₂ exp

( r ²

---+ i 2 n ф

( w ²

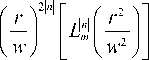
где E 2 – постоянная. Пучок (4) уже не будет модовым пучком и не будет сохранять свою структуру в зоне дифракции Френеля, но он будет сохранять свой вид в дальней зоне. То есть пучок (ЛГ)² будет Фурье-инвариантным и его комплексная амплитуда в фокусе идеальной сферической линзы с фокусным расстоянием f будет иметь вид:

- iz„

E 2 n , m ( P , 6 ) = "^~ E 2 ( - 1) n exP(2 in ⁰ )

x

^                            2

x j x n ' exp ( - x ) |^ L m ( x ) ] J 2 n ( y4x ) dx =             (5)

= —f ⁰- E ₂ ( - 1) ⁿ exp ^ 2 in 6

-

y ²

y

2 n

ni(yL Lm

,

где x = ( r / w )², y = kw p / f , (p, 9) - полярные координаты в Фурье-плоскости. При получении (5) использовался справочный интеграл из [46]. Сравнивая комплексные амплитуды в начальной плоскости (4) и в фокусе сферической линзы (5), видно, что они совпадают с точностью до постоянной. В зоне дифракции Френеля пучок (ЛГ)² будет представлять собой конечную суперпозицию обычных пучков ЛГ, так как комплексная ампли-

туда пучка (4) при любом z вычисляется с помощью преобразования Френеля и равна:

2n

I r ²                II r I

E n ’ m ( r , ф ) = E 3 exp I---+ 1 2 n ф II — I x

’                   I w ²          JI w J

E 2, n , m ( p , 9 , Z )      iz ( - 1 ) )

z

| ikP2         I exp      + 2in9 x

V 2 z          J

f r2 I I r2 I xLn m      ■ Ln+ m      , n > m > 0.

pq

^ w ² J     ^ w ² J

^                            2

x j x ^{| n |} exp ( - px ) [ L m ( x ) ] J 2 n ( y4x ) dx = 0

2n

- iz 0        n I ik p ²           If у I

=---- ( — 1 ) exp       + 2 in 9

z ^V V 2 z        JI 2 J

Г (I n\ + m + 1)

x (6)

л m ! p ^{2 n + 1}

В фокусе сферической линзы ПЛГ-пучок (8) будет сохранять свою структуру, если p = q :

E p , m ( p , 9 ) = — if ⁰- E 3 ( — 1) ⁿ exp(2 in 9 )

X

I У ² I\   ( — 1) s Г ( m — s + 1) Г ( s + 1/2)

X expI I /: :

V 4 p J s = o ( m — s )!      Г ( n + s + 1)

2s x | P — 2 | Tnnl I      У2

x              L21,

V 2 J s ( 2 p (2 — p ) J

x

to xj xn exp (— x) Ln—m (x) Ln+ m (x) J2n (y4x) dx =

— iz                (         у ² J у ^{2 2}

= —^o e (—1) n exp I 2in ф —2L II L I Ln-m+p—q f 3 I                    II ? I p

J                V J V J

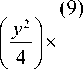
где x = ( p / w )², у = kw p / z , p =1- iz 0 / z , Г( x ) - гамма-функция. При получении (6) использовался справочный интеграл из [46]. В сумме (6) столько слагаемых, сколько колец у пучка ЛГ (1). Из (6) следует, что при m =0 (радиальный индекс пучка нулевой), когда пучок ЛГ имеет одно кольцо, так как L n ( x ) = 1, то сумма в (6) сводится к одному первому слагаемому и пучок (1), амплитуда которого возведена в квадрат, сохраняется при распространении. Это следует также из общего выражения для комплексной амплитуды структурно стабильных пучков [47]:

E ( x , y ) = —exp

q

x ² + у у qw ²

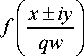
где q = 1 + iz / z 0 , w – радиус перетяжки Гауссова пучка, f ( x ) – любая аналитическая целая функция конечного роста.

Вместо пучка (4) можно рассмотреть более общий Фурье-инвариантный пучок, который представляет собой произведение двух пучков ЛГ (ПЛГ). Комплексная амплитуда ПЛГ-пучка равна:

" n + m—p+q q

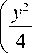
При получении (9) использовался справочный интеграл из [2]. Из (8) и (9) видно, что при p = q и m = 0 ПЛГ-пучок переходит в (ЛГ)²-пучок.

2. Численное моделирование

Нами было проведено численное моделирование фокусировки пучков (ЛГ)2 сферической линзой с помощью авторских скриптов на языке MATLAB. Начальное поле представлялось в виде:

Ез

2,n,m

f r ²

( r , ф ) = exp I---+ i 2 п ф

V w ²

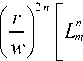
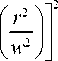
. (10)

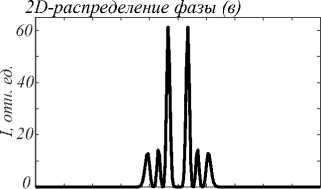
На рис. 1 представлено исходное распределение интенсивности и фазы для (ЛГ)² со следующими параметрами: λ = 532 нм, w =0,5 мм, n =3, m =2.

Фокусировка сферической линзой эквивалентна преобразованию Фурье. Результаты моделирования для пучка (ЛГ)2 в фокусе показаны на рис. 2.

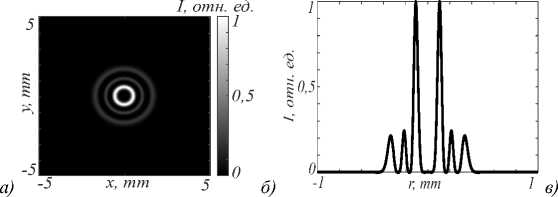
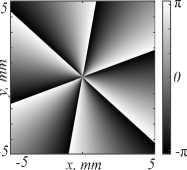
Рис. 1. Исходный пучок (ЛГ) ² : 2D-распределение интенсивности (а); сечение интенсивности вдоль радиуса (б);

Ф, pad

б)

-1

r, mm

¹ в)

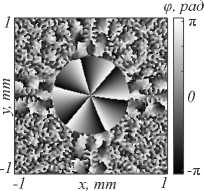
Рис. 2. Поле в фокусе сферической линзы при прохождении через нее исходного пучка (ЛГ) ² : 2D-распределение

интенсивности (а); сечение интенсивности вдоль радиуса (б); 2D-распределение фазы (в)

Рис. 1 и 2 отличаются только на постоянную и наглядно демонстрируют доказанную в первом параграфе Фурье-инвариантность пучков (ЛГ)². Рябь на рис. 2 в вызвана погрешностями, возникающими при численном вычислении преобразования Фурье. В периферийных областях интенсивность близка к нулю, и потому даже небольшие ошибки приводят к изменению фазы на π.

Теперь рассмотрим дифракцию Френеля, которая представляется следующим интегралом:

ikz

E(x,y,z) = -——j|_^ E(x',y',0)x x exp

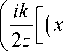
- x ' ) 2 + ( y - y ' ) ² "11 dx ' dy'.

Для его численного расчета были использованы теорема о свертке и свойства преобразования Фурье, которые позволяют вычислить указанный интеграл через комбинацию прямых и обратного преобразований Фурье. Программа для расчета была также реализована на языке MATLAB. Результаты расчетов на разном расстоянии представлены на рис. 3 – 5.

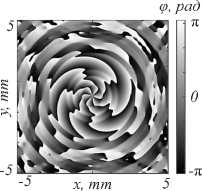
На рис. 3 показаны интенсивность ( а ), ее сечение ( б ) и фаза ( в ) пучка (ЛГ)², показанного на рис. 1, но на расстоянии половины длины Рэлея. Из рис. 3 видно, что вместо трех колец интенсивности (рис. 1) у пучка добавляется четвертое кольцо интенсивности. И яркое кольцо уже не первое (рис. 1), а второе.На рис. 4 показаны интенсивность ( а ), ее сечение ( б ) и фаза ( в ) того же пучка (рис. 1), но на расстоянии Рэлея. Из рис. 4 видно, что пучок имеет 4 светлых кольца, но распределение энергии между ними отличается от распределения энергии на рис. 3

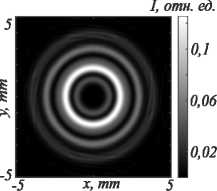
На рис. 5 показано то же самое, что и на рис. 3 и 4, но на расстоянии двух длин Рэлея. В картине интенсивности по-прежнему 4 кольца.

I, отн. ед.

-5

-5 x, mm 5

0,4

0,2

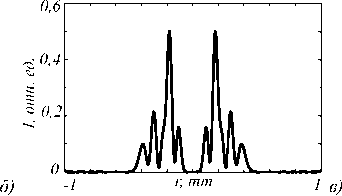
Рис. 3. Поле исходного пучка (ЛГ)² на расстоянии z = z 0 / 2 (z 0 ≈ 1,476 м): 2D-распределение интенсивности (а);

а)

сечение интенсивности вдоль радиуса (б); 2D-распределение фазы (в)

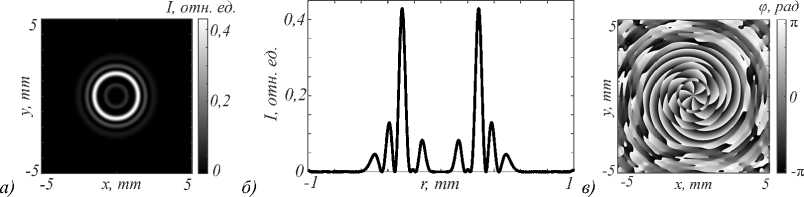
Рис. 4. Поле исходного пучка (ЛГ)² на расстоянии z = z 0 (z 0 ≈ 1,476 м): 2D-распределение интенсивности (а); сечение интенсивности вдоль радиуса (б); 2D-распределение фазы (в)

а)

0,12

0,06

б)

-1

r, mm

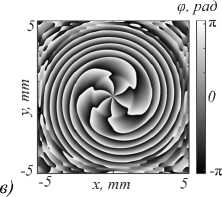
Рис. 5. Поле исходного пучка (ЛГ)² на расстоянии z = 2z 0 (z 0 ≈ 1,476 м): 2D-распределение интенсивности (а); сечение

интенсивности вдоль радиуса (б); 2D-распределение фазы (в)

На рис. 6 показаны вместе распределения интенсивности того же пучка, что и на рис. 1 – 5. Из рис. 6 видно, что на расстоянии 10 длин Рэлея (начало дальней зоны дифракции) в сечении пучка опять остаются 3 светлых кольца, и самое яркое кольцо будет первым от центра кольцом. А на расстоянии 15 длин Рэлея распределение интенсивности совпадает с начальным распределением интенсивности, отличаясь только по масштабу. Таким образом, моделирование подтвердило все теоретические предсказания.

Заключение

В данной работе был рассмотрен новый тип вихревых пучков, пересекающийся с семейством хорошо известных пучков ЛГ. У этих пучков многочлен Ла-герра взят в квадрате, и они называются пучки Лагер-ра–Гаусса в квадрате (ЛГ)2. Пучки ЛГ с нулевым радиальным индексом и четным азимутальным индексом совпадают с (ЛГ)2. Показано теоретически и численно, что вихревой пучок ЛГ «в квадрате» является Фурье-инвариантным и сохраняет свою структуру в фокусе сферической линзы или в дальней зоне дифракции. В зоне дифракции Френеля такой пучок преобразуется в осевую суперпозицию обычных пучков ЛГ, число которых равно числу колец у пучка ЛГ «в квадрате». Если кольцо всего одно, то пучок является структурно стабильным. Также рассмотрен более общий пучок, являющийся «произведением» двух пучков ЛГ. Такой пучок будет Фурье-инвариантным, если число колец у двух пучков ЛГ в «произведении» одинаковое. Результаты работы могут найти свое применение в оптических коммуникациях [40–42].

z = 0		z = z 0 /4		z = z 0 /2
о		©		©
R=5 mm		R=5 mm		R=10 mm
z = 3z 0 /4		z = z 0		z = 2z 0
о		о
R=10 mm		R=10 mm		R=10 mm
z = 5z 0		z = 10z 0		z = 15z 0
о		о		(©)
R=20 mm		R=50 mm		R=50 mm

Рис. 6. Распределения интенсивности пучка (ЛГ)² при λ = 532 nm, w = 0,5 mm (z 0 ≈ 1,476 m), n = 3, m = 2 на расстоянии z в квадратной подобласти шириной 2R

Работа выполнена при поддержке Российского научного фонда, грант № 22-12-00137.