Вихревые дифракционные линзы для формирования вихревых световых пучков
Автор: Скиданов Роман Васильевич, Ганчевская София Владиславовна
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 5 т.39, 2015 года.
Бесплатный доступ
Рассмотрено формирование вихревых световых пучков с помощью вихревой параболической линзы. Показано, что при формировании такого пучка складываются топологические заряды структуры вихревой линзы и топологические заряды отдельных зон вихревой линзы.
Вихревой световой пучок, вихревая линза, топологический заряд
Короткий адрес: https://sciup.org/14059409
IDR: 14059409 | DOI: 10.18287/0134-2452-2015-39-5-674-677
Текст научной статьи Вихревые дифракционные линзы для формирования вихревых световых пучков
Вихревые световые пучки известны довольно давно [1, 2].
Вихревые пучки могут быть сформированы с помощью специальных решёток [2, 3, 7] или с помощью спиральной фазовой пластины [5]. Можно также использовать вихревую зонную пластинку [8]. Также есть работы, в которых вихревые световые пучки формируют с использовании деформируемого сегментного зеркала [12] или за счёт использования плазмонных эффектов [14].
Можно формировать вихревые световые пучки с помощью резонатора лазера, внутри которого расположена спиральная фазовая пластина [8]. Такие пучки также формируются из пучков Гаусса–Эрмита с помощью преобразователя, состоящего из сферической и цилиндрический линзы [4, 5]. Наличие у таких пучков орбитального углового момента определяет их основное использование для оптического вращения микрообъектов [9], оптической передачи информации [13].
Вихревыми также являются пучки Бесселя и Гаус-са–Лагерра [6, 11]. В [11] было рассмотрено формирование пучков Бесселя вихревыми аксиконами. При этом было показано, что топологические заряды структуры таких аксиконов и топологические заряды зон складываются, что даёт возможность формирования пучка Бесселя заданного порядка практически бесконечным количеством фазовых дифракционных оптических элементов. В данной работе представлен способ формирования простых вихревых пучков за счёт использования нового типа дифракционных оптических элементов – вихревых линз, подобных представленным в [8], но с добавленными топологическими зарядами зон, как у вихревых аксиконов в [11].
где m 1, m 2 – номера дополнительных вихревых составляющих, r, φ – полярные координаты, ν – пространственная несущая частота, n – топологический заряд бинарного дифракционного аксикона, который является основой структуры этого ДОЭ. В настоящей работе будем рассматривать элементы, у которых m 1 = m 2 = m , но при этом существует дополнительный поворот на π/m для разделения зон. Такие элементы, как было показано в [11], формируют пучки Бесселя. В настоящей работе мы рассмотрим похожий элемент, у которого в формуле появляется квадратичная зависимость от r . Таким образом, формула (1) превращается для таких элементов в
т( r, ф) = e™ф • sgn
| k i cos r +
I f
n ф
где f – фокусное расстояние вихревой линзы, которая является основой структуры этого ДОЭ. Будем в дальнейшем называть такой элемент вихревой линзой. Точно так же, как в [11], с помощью разных сочетаний топологических зарядов структуры и зон рассчитывалась фазовая функция бесконечного количества элементов, каждый из которых формирует пучок Бесселя заданного порядка, этот элемент в своей фокальной плоскости будет формировать вихревой световой пучок заданного порядка, при этом таких фазовых функций можно сформировать также практически бесконечное количество.
1. Вихревая линза
В [11] описываются дифракционные оптические элементы нового типа, которые имеют функции пропускания вида
т( r, ф) = 2 [exp (im^ + exp (im 2ф)] +
+
[ exp ( im 2 ф ) - exp ( ™ 1 ф ) ] sgn [ cos ( 2 nv r + n ф ) ] ,
На рис. 1 представлен характерный вид такой вихревой линзы.

Рис. 1. Характерный вид вихревой линзы: топологический заряд структуры n = 1, топологический заряд зон m = 2, f = 270 мм
2. Формирование вихревых световых пучков
Моделирование дифракции на вихревых линзах осуществлялось с помощью преобразования Френеля. На рис. 2 представлен ряд изображений вихревых линз с разными сочетаниями топологических зарядов структуры зон (рис. 2 а , г , ж , к ), а также распределений интенсивностей (рис. 2 б , д , з , л ), сформированных на расстоянии 270 мм. Все представленные элементы формируют вихревой световой пучок 1-го порядка.

л)
м) L_
Рис. 2. Фазовые функции вихревых линз с топологическими зарядами структуры и зон (n, m) соответственно (0,1) (а), (1, 0) (г), (-1,2) (ж), (-2,3) (к), а также формируемые ДОЭ с этими фазовыми функциями распределения интенсивности на расстоянии 270 мм (б, д, з, л) и фазы (в, е, и, м)
ж)
Как видно из рис. 2, совершенно разные по фазовой функции ДОЭ формируют одинаковые вихревые световые пучки с единичным топологическим зарядом (рис.2 в, е, и, м ). При этом на рис. 2 следует отметить два вырожденных случая вихревых линз. При нулевом заряде зон (рис. 2г ) мы получаем бинарную фазовую линзу, описанную в [10], а при нулевом заряде структуры (рис. 2 ж ) получается обычная параболическая линза, в каждой зоне которой добавлен топологический заряд.
Точно так же можно показать, что очень похожие друг на друга по фазовой функции ДОЭ могут формировать вихревые световые пучки с карди- нально отличающимися топологическими зарядами (рис. 3).


а)
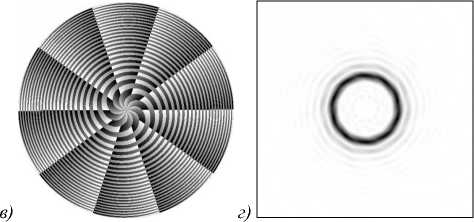
Рис. 3. Фазовые функции вихревых линз с топологическими зарядами структуры и зон соответственно (-5, 5) (а), (-5, -5) (в), а также формируемые ДОЭ с представленными фазовыми функциями распределения интенсивности на расстоянии 270 мм (б, г)
Как видно из рис. 3, весьма похожие по структуре ДОЭ формируют пучок, похожий на Гауссов (топологический заряд =0), и вихревой световой пучок с топологическим зарядом -10. Таким образом, представленные ДОЭ позволяют формировать любой вихревой пучок бесконечным количеством способов, что особенно удобно для формирования суперпозиций вихревых световых пучков (рис. 4). На рис. 4 представлены бинарные фазовые функции таких ДОЭ с f = 270 мм, полученные путём линейного кодирования исходных фазовых функций.
Как видно из рис. 4, закодированные бинарные элементы, формирующие одинаковые вихревые пучки, имеют сильно отличающиеся друг от друга фазовые функции. Следует заметить, что одинаковые пучки получаются в этом случае только в одном порядке, т.к. в другом порядке меняется знак операции, т.е. вместо сложения получается вычитание. Для элемента на рис. 4 в это важно, т.к. оба топологических заряда отличны от 0.
а)


б)

Рис. 4. Фазовые функции вихревых линз с топологическими зарядами структуры и зон соответственно (0,1) (а), (-2, 3) (в), кодированные линейно, и распределения интенсивности на расстоянии 270 мм (б, г)
Заключение
Описан новый вид дифракционных оптических элементов, которые за счёт использования топологических зарядов структуры и топологических зарядов зон позволяют бесконечным количеством способов формировать оптические вихри заданного порядка в зоне дифракции Френеля.
Работа выполнена за счёт Российского научного фонда (грант 14-19-00114).
Список литературы Вихревые дифракционные линзы для формирования вихревых световых пучков
- Khonina, S.N. The phase rotor filter/S.N. Khonina, V.V. Kotlyar, M.V. Shinkaryev, V.A. Soifer, G.V. Uspleniev//Journal of Modern Opics. -1992. -Vol. 39, Issue 5. -P. 1147-1154. -DOI: DOI: 10.1080/09500349214551151
- Abramochkin, E. Generation of spiral-type laser beams/E. Abramochkin, N. Losevsky, V. Volostnikov//Optics Communications. -1997. -Vol. 141, Issues 1-2. -P. 59-64. -DOI: DOI: 10.1016/S0030-4018(97)00215-0
- Oron, R. Efficient formation of pure helical laser beams/R. Oron, N. Davidson, A.A. Friesem, E. Hasman//Optics Communications. -2000. -Vol. 182. -P. 205-208.
- Abramochkin, E. Beam transformations and nontransformed beams/E. Abramochkin, V. Volostnikov//Optics Communications. -1991. -Vol. 83, Issues 1-2. -P. 123-135. -DOI: DOI: 10.1016/0030-4018(91)90534-K
- Beijersbergen, M.W. Astigmatic laser mode converters and transfer of orbital angular momentum/M.W. Beijersbergen, L. Allen, H.E.L.O. van der Veen, J.P. Woerdman//Optics Communications. -1993. -Vol. 96. -P. 123-132.
- Allen, L. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes/L. Allen, M.W. Beijersbergen, R.J.C. Spreeuw, J.P. Woerdman//Physical Review A. -1992. -Vol. 45. -P. 8185-8189.
- Bazhenov, V.Y. Screw dislocations in light wavefronts/V.Y. Bazhenov, M.S. Soskin, M.V. Vasnetsov//Journal of Modern Opics. -1992. -Vol. 39. -P. 985-990.
- Heckenberg, N.R. Generation of optical phase singularities by computer-generated holograms/N.R. Heckenberg, R. McDuff, C.P. Smith, A.G. White//Optics Letters. -1992. -Vol. 17. -P. 221-223.
- Padgett, M.J. The angular momentum of light: optical spanners and the rotational frequency shift/M.J.Padgett, L. Allen//Optical and Quantum Electronics. -1999. -Vol. 31. -P. 1-12.
- Скиданов, Р.В. Дифракционные оптические элементы для формирования комбинаций вихревых пучков в задаче манипулирования микрообъектами/Р.В. Скиданов, С.В. Ганчевская//Компьютерная оптика. -2014. -Т. 38, № 1. -С. 65-71.
- Скиданов, Р.В. Формирование пучков Бесселя вихревыми аксиконами/Р.В. Скиданов, С.В. Ганчевская//Компьютерная оптика. -2014. -Т. 38, № 3. -С. 463-468.
- Tyson, R.K. Generation of an optical vortex with a segmented deformable mirror/R.K. Tyson, M. Scipioni, J. Viegas//Applied Optics. -2008. -Vol. 47(33). -P. 6300-6306.
- Gibson, G. Free-space information transfer using light beams carrying orbital angular momentum/G. Gibson, J. Courtial, M. Padgett, M. Vasnetsov, V. Pas'ko, S. Barnett, S. Franke-Arnold//Optics Express. -2004. -Vol. 12. -P. 5448-5456.
- Genevet, P. Ultra-thin plasmonic optical vortex plate based on phase discontinuities/P. Genevet, N. Yu, F. Aieta, J. Lin, M.A. Kats, R. Blanchard, M.O. Scully, Z. Gaburro, F. Capasso//Applied Physics Letters. -2012. -Vol. 100. -P. 013101-1.


