Вихревые лазерные пучки, комплексная амплитуда которых пропорциональна произведению двух функций Бесселя

Пучки Бесселя [1] и Бесселя–Гаусса [2] известны в оптике с 1987 года. По пучкам Бесселя имеются современные обзоры [3]. До сих пор внимание к ним не ослабевает из-за их широкого применения в задачах наноструктурирования материалов [4 – 5], манипуляции микрочастицами [6 – 7], ускорения атомов [8 – 9], микроскопии [10 – 11] и беспроводной оптической связи [12 – 13]. Среди множества пучков Бесселя известны различные модификации. В [14] рассмотрены пучки Бесселя–Гаусса с полуцелым номером и аргументом, зависящим квадратично от радиальной переменной. В [15] рассмотрен другой пучок Бесселя с полуцелым номером, квадратичным аргументом и конечной энергией, но без гауссовой огибающей. В [16] рассмотрены асимметричные пучки Бесселя–Гаусса, которые близки к рассматриваемым здесь пучкам, но вместо двух «месяцев» их интенсивность имеет вид одного «месяца». В работе [17] пучки Бесселя–Гаусса детально сравниваются с пучками Лагерра-Гаусса. А в [18] рассматриваются обобщенные (или дуальные) пучки Лагерра–Гаусса. Двойные и квадратные пучки Бесселя–Гаусса рассмотрены в [19].

Помимо использования узкой кольцевой диафрагмы [1], что, конечно, очень неэффективно для освещения, можно формировать пучки Бесселя с помощью деформируемого зеркала, пространственного модулятора света, матрицы микрозеркал, бинарной маски [20], голограммы [21], с помощью аксикона и линзы (или второго аксикона) для формирования яркого кольца [22 – 24] или с использованием тороидального резонатора [25].

В данной работе рассмотрено новое однопараметрическое семейство пучков Бесселя–Бесселя–Гаусса (ББГ-пучки), которое описывается комплексной амплитудой в виде произведения гауссовой функции и двух функций Бесселя n-го порядка с похожей зависимостью аргумента от цилиндрических координат. Показано, что топологический заряд такого пучка можно изменять, изменяя величину положительного параметра. Также показан аномально быстрый поворот интенсивности пучка при распространении в ближней зоне дифракции. При прохождении от перетяжки расстояния много меньше длины Рэлея интенсивность поворачивается почти на 45 градусов. Рассмотрены еще два аналогичных вихревых ББГ-пучка: с четырьмя локальными максимумами интенсивности, лежащими на декартовых осях координат, и с одним максимумом интенсивности в виде полумесяца, центр которого лежит на горизонтальной оси.

1. Пучки Бесселя–Бесселя–Гаусса на основе пучков Бесселя–Гаусса

Хорошо известны пучки Бесселя–Гаусса [2], комплексная амплитуда которых описывается выражением:

k – волновое число света, w – радиус перетяжки гауссова пучка, ( r , φ, z ) – цилиндрические координаты, z – оптическая ось, α – масштабный множитель, определяющий ширину функции Бесселя J n ( x ), n – целое число, топологический заряд оптического вихря. Используя ряд из функций Бесселя (раздел 5.7.8 в [26]):

E bg ( г , ф , z ) = —1-exP q ( z )

i a ² z

r ²

2 kq ( z ) w ² q ( z )

+ in ф lx

®     *2 1 + n

У-------- J-U ₊„( x ) =

! ■? l !( l + n )!

T (     ( 1     • 4 1 ^^ A ( 1     • 4 1 ^^ ⁽

= J„ \ x sin — arcsin— J„ x cos — arcsin— ,

I 1 2 x )) I 1 2 x ) )

где q ( z ) = 1 + iz / z 0 , z 0 = kw ² /2 - длина Рэлея,

можно записать комплексную амплитуду новых вихревых лазерных пучков Бесселя–Бесселя–Гаусса (ББГ-пучки):

„ , \ 1 ^{( 1} a z E bbg ( r , ф , z ) = -exp l -—— q L 2 kq

2 1 + n

( ce i ^ф)

J 2 ^{l +} l ! ( l + n ) !

ar । 1 | ia2z r2 । — l = — exp |----l x q ) q    L 2 kq w2 q)

x J .

a ² r ²

16 c ² q ² e ² - 'ф ) \ j,

a ² r ²

, q = q ⁽ z ),

где с – параметр, который будем считать действительным и положительным. Но если бы параметр с был комплексным, c = | c | e‘0 , то под корнем аргумент последнего слагаемого был бы равен 2(φ + θ). И картина интенсивности пучка (3) вместе с нулями интенсивности была бы просто повернутой на угол –θ. Из (3) видно, что комплексная амплитуда ББГ-пучков записана для любого z в явном виде. Устремляя z к бесконечности, из (3) можно получить комплексную амплитуду ББГ-пучков в дальнем поле. Из (3) также видно, что ББГ-пучки не обладают круговой симметрией, но обладают осевой симметрией, так как замена азимутального угла φ на угол φ + π не приведет к изменению амплитуды (3). Если в ряду (3) положить φ = πp, p = 0,1,2…, то коэффициенты под знаком суммы для разных номеров l будут положительные, то есть все БГ-пучки в ряду будут складываться в фазе и интенсивность на горизонтальной оси должна быть большой. А на вертикальной оси (при φ = π /2+ πp) коэффициенты ряда (3) будут менять знаки, и поэтому соседние пучки БГ будут складываться в противофазе и интенсивность на вертикальной оси будет меньше, чем на горизонтальной. Устремляя радиальную координату к нулю (r^0) и воспользовавшись только первым членом разложения в ряд функций Бесселя при малом аргументе,

, 1 ( x Л ⁿ

^J n ( x <<  1 ) »—1-| ,                              ⁽⁴⁾

n ! L 2 )

вместо (3) получим амплитуду ББГ-пучка вблизи нуля интенсивности на оптической оси:

E bbg ( r <<  1, ф , z ) »

1           ( i a ² z

-----— exp |--

4 ⁿ ( n ! ) q    L ^{2 kq}

a ² r ²

n /2

16 c ² q ² e ² i ^ф ) |

x

x

a r l /“V --- a r + Ja² r

2 q ^{2 (     V}

16 c ² q ² e ² i ^ф

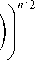
exp 2^{3 n} ( n !)² q

i a² z r ² L _{v z} , ---( a r ) ( a ² r ²

2 kq  w ² q /  ^{1 V}

-a ² r ² + 16 c ² q ² e ² i ^ф) n /2 =

1 2^{3 n} ( n !)² q

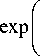
i a 2 z ^r Ъ_сы^-1«Г(^ф-’> Г 2 kq w 2 q ^{14 cq a) 1 re} ) ,

z tg V = — . z 0

Из (5) видно, что вблизи нуля на оптической оси амплитуда пучка (3) описывает оптический вихрь с топологическим зарядом n . Также из (5) видно, что угол поворота интенсивности при распространении пучка увеличивается против часовой стрелки пропорционально фазе Гоу: φ = ψ. Если в (3) устремить к нулю радиальную координату ( r ^ 0) внутри ряда, то в ряду останется самое большое слагаемое, а именно, первое слагаемое, и, вместо (3), можно записать:

Ebbg (r << 1,ф,z)» ^-exp| qn! L ia2z r2 । ----l x

2 kq  w ² q )

x ( ce “ ^f ) n J_n

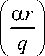
Выражение (6) верно при малом параметре c. Из (6) видно, что вблизи центрального нуля интенсивности ББГ-пучок совпадает с БГ-пучком (1), если положить, что c = (n!)–1/n. Из (3) и особенно из (6) видно, что при c =0 амплитуда ББГ-пучка становится нулевой. Из (3) также видно, что в начальной плоскости, когда z =0 и q(z) = 1 аргументы функций Бесселя будут действительными величинами при некоторых значениях азимутального угла: φ = πp /2, p=0, 1, 2, … То есть на декартовых осях x и y аргументы у обеих функций Бесселя в (3) будут действительными и при некоторых значениях радиальной переменной r могут быть равны корням функций Бесселя Jn(уn,p), p = 1, 2, 3, .... Приравняем аргументы функций Бесселя в начальной плоскости на декартовых осях действительным корням функций Бесселя, получим (φ = πp /2):

a r ( а r ± 4 а ² r ² ± 16 c ² ) = 2 у П , _p

В (7) знак минус под квадратным корнем имеет место на горизонтальной оси x , а знак плюс – на вертикальной оси y . Знаки плюс и минус перед квадратным корнем в (7) относятся к разным функциям Бесселя в (3). В (7) на вертикальной оси y под корнем нужно выбрать знак плюс, тогда, чтобы левая сторона (7) была положительной, перед корнем нужно выбрать только плюс. Поэтому можно однозначно определить координаты нулей функций Бесселя на вертикальной декартовой оси:

ryp = ±—2^ , а 4 c2 +у n,

.

Плюс и минус в (8) означают положительные и отрицательные координаты нулей интенсивности ББГ-пучка на вертикальной оси в начальной плоскости. Из-за того, что под корнем в (7) на вертикальной оси будет знак плюс, второе слагаемое (7) будет больше, чем первое, то есть под внешним корнем первой функции Бесселя в (3) на вертикальной оси будет отрицательное число и аргумент будет чисто мнимым:

ar (ar - д/а2г2~+16С2) =

'a² r ² + 16 c ² - a r ) .

Знаки плюс и минус перед корнем в (9) показывают неоднозначность корня квадратного от минус единицы. Знак нужно выбирать так, чтобы решение было непрерывным. Если номер функции Бесселя четный, то неоднозначности нет, так как оба знака в (9) приводят к одному результату:

Jn (±ix) = (±i)n In (X) = (±i)2p 12p (X) = (-1)p 12p (X), где In(x) – модифицированная функция Бесселя.

На горизонтальной оси x в (7) следует выбрать под корнем знак минус. Тогда для неотрицательности подкоренного выражения нужно, чтобы выполнялось неравенство:

r >  4 c / a.

Если постоянная асимметрии с большая, 4 c >>α, то неравенство показывает, что на горизонтальной оси нули функции Бесселя (нули интенсивности) будут появляться дальше от центра, чем нули на вертикальной оси. Также из (10) следует, что нули интенсивности на горизонтальной оси будут расположены дальше максимального значения интенсивности, то есть радиусы двух максимумов интенсивности будут линейно расти с ростом постоянной с и будут примерно равны: r max ® ± 4 c / a . Координаты нулей интенсивности на горизонтальной оси равны:

Y =4- r_xp

Y П , p

a^ ² , p — 4 c ²

Выражение (11) верно при условии (10) и при следующем условии, обеспечивающем положительность подкоренного выражения в (11):

Y n , p >  2 c .

Заметим, что нули интенсивности (локальные оптические вихри), которые лежат на декартовых осях, имеют чередующиеся знаки (топологический заряд равен +1 или – 1) так, что соседние оптические вихри компенсируют друг друга. Это относится ко всем нулям, кроме центрального вырожденного нуля, топологический заряд которого равен n . Топологический заряд (ТЗ) ББГ-пучков увеличивается с ростом параметра асимметрии c >0. Если первый член ряда в (3) наибольший из всех, то ТЗ пучка (3) равен n . Это будет иметь место, если параметр асимметрии небольшой и удовлетворяет примерно неравенству: с <  n . Если параметр c увеличивается, то ТЗ ряда (3) будет равен ТЗ второго слагаемого, то есть будет равен n +2. При дальнейшем увеличении постоянной с уже третье слагаемое в ряде (3) может стать по амплитуде (при малом r ) больше остальных, и тогда ТЗ суперпозиции всех БГ-пучков, входящих в ряд, будет равен n +4 и т.д. Устремляя значение постоянной к бесконечности, ТЗ ряда (3), а значит, и ББГ-пучков, также будет стремиться к бесконечности. При распространении пучка (3) в свободном пространстве нули интенсивности разных знаков на декартовых осях пропадают (аннигилируют) и остаются только оптические вихри вблизи начала координат.

• 2. Пучки Бесселя–Бесселя–Гаусса на основе пучков Бесселя–Гаусса с квадратичным аргументом

В работе [14] найдено решение параксиального уравнения Гельмгольца:

I- + -+ 2 ik -I E ( x , y , z ) = 0             (13)

^ox2 dy2      dz J в виде произведения функции Гаусса на функцию Бесселя с полуцелым номером и аргументом в квадрате (БГ2-пучки) [14]:

E bg 2 ( r , ф , z )

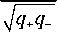
" i ( 1 + P ² w ⁴ ) zr ²      r ²      . \ f P r ²

---------;---;--+ ^{in ф} I J n /21 ------

I    z 0 w² q + q -      w² q ₊ q -       ) | q ₊ q -

На основе пучков (14) и ряда (2) можно построить пучки Бесселя–Бесселя–Гаусса-2 (ББГ2-пучки) с полуце-лым номером и сложной зависимостью аргументов:

E bbg 2 ( r , ф , z ) =

exp q + q -

f i ( 1 + P ² w ⁴ ) zr ²

2 ~ ~ z 0 w² q + q -

2 ~ ~ w² q + q -

z

2 1 + n /2

( ce ^{2 ф})

г I P r2

'J 2 1 + n /2 I

I I q + q -

exp q + q -

f i ( 1 + P ² w ⁴ ) zr ²

z о w ² q + q -

w ² q + q -

J n /2

16 c ²( q ₊ q - )⁴ e ⁴ i ^ф ) | x

^x J n /2

16 c ² ( q ₊ q - )⁴ e ⁴ i ^ф ) | ,

где q ± = 1 ± P w ² z/z 0 + iz/z 0 , в - действительная постоянная величина, определяющая масштаб функции Бесселя. Семейство пучков (15), зависящих от параметра c , который мы рассматриваем как действительное число, имеет конечную энергию из-за наличия гауссовой экспоненты. При c =0 пучок (15) становится нулевым при n, отличном от нуля, или равен пучку Бесселя–Гаусса–2 (14) нулевого порядка с квадратичным аргументом при n =0. Аналогично (6) вблизи оптической оси (при малом r ) пучок (15) становится равным порождающему пучку (14). Из анализа ряда в (15) видно, что при углах 2φ = πp, p =0, 1, 2…, коэффициенты под знаком суммы для разных номеров l будут положительные, то есть все ББГ2-пучки в ряду (15) будут складываться в фазе и интенсивность на декартовых координатах должна быть большой. А при условии 2φ = π /2+ π p коэффициенты ряда (15) будут менять знаки и поэтому соседние пучки ББГ2 будут складываться в противофазе, и интенсивность на диагоналях четырех квадрантов будет меньше, чем интенсивность на декартовых осях. То есть можно предположить, что ББГ2-пучки будут иметь четыре локальных максимума (четыре лепестка интенсивности) на декартовых осях на некотором расстоянии от оптической оси. Аналогично (7) приравняем аргумент функций Бесселя в (15) корням Бесселя с полуцелым номером в начальной плоскости ( z =0) на 8 лучах при углах φ = π p /4, p =0, 1, 2,…:

P r ² ( P r ² ±VP ² r ⁴ ± 16 c ² ) = 2 y n /2, p . (16)

При углах φ = π p /4, p = 1, 3, 5…, знак под корнем будет положительный, и тогда координаты нулей функции Бесселя будут находиться в точках на 4 диагоналях с координатами:

дет действительной величиной при условии, аналогичном (10):

r >  2

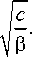
В (18) нужно потребовать, чтобы параметр с был больше нуля. Координаты корней функций Бесселя в (15) следует искать при условии (18) на декартовых осях из следующего уравнения:

r x

= ±

У n /2, p

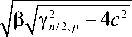
Чтобы выражение (19) было действительным, следует потребовать выполнения условия, аналогичного (12): у _{n /2} , _p >  2 c . Эти корни функций Бесселя в (15), лежащие на декартовых осях и диагоналях (на 8 лучах), являются центрами оптических вихрей первого порядка с чередующимися знаками + 1 и – 1. Поэтому эти вихри не изменяют топологический заряд пучка (15), который равен топологическому заряду центрального оптического вихря n . При распространении в свободном пространстве аргументы функций Бесселя в (15) становятся комплексными, поэтому все нецентральные оптические вихри компенсируют друг друга и пропадают. В сечении пучка (15) при z >0 остается только центральный оптический вихрь.

3. Пучки Бесселя–Бесселя–Гаусса второго типа

В справочнике [27] можно найти другой ряд, похожий на ряд из функций Бесселя (2):

” ( n + 1/2 ) l t l ^{+ n z} 1 !(2 n + 1) i

= 22nn! Jn (x + ^

J i + n (2 x ) =

Г =4- xyp

У n /2, p

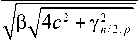
При четных р на лучах φ = π p /4, p =0, 2, 4…, знак под корнем в (16) будет отрицательный и корень бу-

' x ² - tx ) J_n ( x - -J x ² - tx ) ,

где ( a ) k = a ( a + 1)( a + 2)…( a + k – 1) – символ Пох-гаммера.

На основе ряда (20) и БГ-пучка (1) можно получить ББГ-пучки второго типа (2ББГ-пучки):

1     ( i a ² z   r ² \n(ⁿ + ^1/2 )/( ce ’ )        ( ^a r У  1     ( i a ² z   r 2 У

E2 bbg (r, Ф, z) = -exPl —---— |1                  J+n I    I =-exPl —---— Iх q    ^ 2kq   w2qJ l=0 2nn!l!(2n +1)l       ^ q J  q    ^ 2kq   w2q J

X J n

a ² r ²

2 c a rqe i ’ ) I J_n

a ² r ²

, q = q ^{( z}).

При c =0 2ББГ-пучки равны нулю, при n , отличном от нуля, и равны БГ-пучку нулевого порядка, если n =0. Из (21) видно, что только на горизонтальной оси x значения ряда будут действительными в начальной плоскости. При этом на положительной части горизонтальной оси (φ = 2π p , p =0, 1, 2…) все слагаемые ряда будут складываться «в фазе», и поэтому величина интенсивности будет большая. А на отрицательной части оси x (φ = π p , p = 1, 3, 5…) соседние слагаемые будут складываться в «противофазе», и поэтому интенсивность будет меньше, чем на положительной части оси x . То есть распределение интенсивности в начальной плоскости будет иметь один максимум при x >0. Приравняем аргументы функций Бесселя в (21) корням γ n,p в начальной плоcкости ( z =0) на отрицательной части горизонтальной оси x <0, получим координаты нулей интенсивности:

=      2 y 2, p

x <0 a( c + 2y n, p)

На положительной части горизонтальной оси x > 0 координаты нулей интенсивности можно найти только при условии, аналогичном (10):

r >  2 c/ a .

При условии (23) координаты нулей интенсивности будут равны:

Г х >

2 Y 2, p a ( 2 y n , p - c ) ,

2 y n , p >  c .

Из сравнения (22) и (24) видно, что при увеличении параметра асимметрии с нули интенсивности при x <0 будут приближаться к центру, а при x >0 – удаляться от центра. В центре на оптической оси будет находиться нуль интенсивности, который является центром оптического вихря с топологическим зарядом n . Нули интенсивности (22) и (24), лежащие на горизонтальной оси, являются центрами оптических вихрей с топологическими зарядами +1 и – 1. При распространении пучка эти периферийные оптические вихри «аннигилируют», так как аргумент функций Бесселя в (21) становится комплексным. У функции Бесселя имеются только действительные корни, комплексных корней нет.

4. Моделирование распространения ББГ-пучков

На рис. 1 показаны распределения интенсивности и фазы ББГ-пучка, рассчитанные по формуле (3) для следующих параметров: длина волны λ = 532 нм, радиус перетяжки w 0 = 1 мм, порядок n =4, масштаби-

рующий множитель пучков БГ α = k / 1000, параметр асимметрии c = 5. Разные интенсивности и фазы показаны на следующих расстояниях от перетяжки: z =0, 0,15 z 0 , 0,25 z 0 , 0,5 z 0 , z 0 , 1,5 z 0 . Из рис. 1 видно, что после прохождения расстояния много меньше длины Рэлея ББГ-пучок повернулся против часовой стрелки почти на 45 градусов. При прохождении расстояния, равного длине Рэлея, ББГ-пучок (3) повернулся почти на 90 градусов, и при дальнейшем распространении медленно доворачивался до 90 градусов. Обычно вихревые пучки с распределением интенсивности без радиальной симметрии поворачиваются на 45 градусов после прохождения расстояния, равного длине Рэлея [28, 29]. Дело в том, что у пучка Бесселя (3) дальняя зона наступает при меньших расстояниях, чем длина Рэлея. Радиус гауссова пучка можно рассматривать как диафрагму, ограничивающую пучок Бесселя, и поэтому после расстояния wk / α = 1000 w = 1 м, для пучка Бесселя уже наступает дальнее поле, хотя длина Рэлея равна примерно z 0 = 6 м.

На рис. 2 показаны распределения интенсивности и фазы ББГ-пучков (3) при следующих параметрах: длина волны λ = 532 нм, радиус перетяжки w 0 = 1 мм, топологический заряд n =4, масштабирующий множитель α = k / 1000, параметр асимметрии c = 1, 2, 3, 4, 5, 6, 7, 8, расстояние распространения z = z 0 . Полуразмер расчётной области R = 10 мм.

Из рис. 2 видно, что с увеличением постоянной c растет значение топологического заряда ББГ-пучка. Так, при с от 1 до 3 ТЗ равен n =4, при с , равном 4 и 5, ТЗ равен n +2=6, при с , равном 6 и 7, ТЗ равен n +4 =8, и при с , равном 8, ТЗ равен n +6= 10. То есть мы показали, что с помощью изменения параметра c можно управлять топологическим зарядом ББГ-пучков (3), изменяя его на четное число. Кроме того, из рис. 2 видно, что в начальной плоскости расстояние между двумя максимумами интенсивности на горизонтальной оси увеличивается пропорционально постоянной c , как и предсказывает теория (23). Расстояние от центра до одного из полумесяцев в первом столбце на рис. 2 можно оценить, зная первые корни первых функций Бесселя, входящих в (3). Например, при c = 1 основной вклад в ряд (3) вносит первый член, пропорциональный функции Бесселя 4-го порядка. Первый корень функции Бесселя 4-го порядка 7,3. Тогда, приравнивая аргумент первой в ряду функции Бесселя в (3) в начальной плоскости α r половине значения первого корня, получим примерное расстояния до полумесяца – 310 мкм (точное расстояние равно 440 мкм). При больших c надо брать пер-

вые корни функций Бесселя более высокого порядка. Точные расстояния до полумесяца в начальной плоскости на рис. 2 (первый столбец) при разных c такие: 479 мкм (с =2), 537 мкм (с =3), 655 мкм (с =4), 772 мкм (с =5). Радиус неоднородного кольца интен- сивности на рис. 2в увеличился по сравнению с радиусом интенсивности в перетяжке (рис. 2а) примерно в 10 раз. Размер радиуса этого кольца можно оценить по формуле z0 α / k = z0 / 1000 = 6,2 мм. Это согласуется с рис. 2в (радиус кольца – 5,8 мм).

Рис. 1. Распределения интенсивности (строка 1) и фазы (строка 2) ББГ-пучков, рассчитанные по формуле (3) на разных расстояниях от перетяжки: z = 0, 0,15z 0 , 0,25z 0 , 0,5z 0 , z0, 1,5z 0 . Полуразмер расчётной области R = 10 мм при z = 1,5z 0 и z = 2z 0 R = 20 мм. Шкала показывает 1 мм (а – в, д – е) и 10 мм (г)

Рис. 2. Распределение интенсивности (строки 1 и 3 ) и фазы (строки 2 и 4) ББГ-пучка (3) в начальной плоскости (строки 1 и 2) и на расстоянии Рэлея (строки 3 и 4) при разных параметрах с: 1 (столбец а), 2 (столбец б), 3 (столбец в), 4 (столбец г), 5 (столбец д), 6 (столбец е), 7 (столбец ж) и 8 (столбец з). Полуразмер расчётной области R = 10 мм. Шкала показывает 1 мм

• 5.    Моделирование распространения ББГ2-пучков

Параметры моделирования пучков (15): радиус перетяжки гауссова пучка w0 = 1 мм, топологический заряд n =4, длина волны λ =532 нм, масштабный параметр функции Бесселя р = 10-6 k02, параметр асимметрии изменялся: c = 1; 1,5; 2. Так как пучки (15) сильно расходятся, то интенсивность рассчитывалась на малом расстоянии от начальной плоскости, на десятой части длины Рэлея z = z0 / 10. Половина размера кадра равна R = 5 мм. Полуразмер в начальной плоскости равен R = 1 мм. На рис. 3 – 5 показаны интенсивность пучка в начальной плоскости (радиус начального пучка примерно 0,25 мм) (а) и два распределения интенсивности на расстоянии z = z0 / 10, рассчитанные разными способами: с помощью интегрального преобразования Френеля (б) и с помощью ряда (15) из функций Бесселя с квадратичным аргументом (в). Рис. 3 –5 отличаются выбором разных параметров асимметрии с: 1 (рис. 3), 1,5 (рис. 4), 2 (рис. 5). На рис. 3 – 5 видно, что уже на десятой части расстояния Рэлея пучок увеличивается в диаметре примерно в 10 раз. То есть пучок (19) хотя и параксиальный, так как имеет гауссову огибающую, но расходится гораздо сильнее, чем огибающий гауссов пучок.

Расстояния между максимумами (по горизонтали) в начальной плоскости равны 303 мкм (рис. 3 a ),

322 мкм (рис. 4 а ), 342 мкм (рис. 5 а ). На расстоянии z 0 / 10 между максимумами оказались равны 4221 мкм (рис. 3 б , в ), 4396 мкм (рис. 4 б , в ), 4669 мкм (рис. 5 б , в ). Таким образом, за такое небольшое расстояние распространения ширина пучка увеличилась в 13,9 ( c = 1), 13,6 ( c = 1,5), 13,7 ( c =2) раз.

Рис. 3. Интенсивность в начальной плоскости (a), полученная через произведение функций Бесселя, а также интенсивности (б, в) на расстоянии z = z 0 / 10, полученные через преобразование Френеля (б) и через ряд (15) квадратичных пучков Бесселя–Гаусса (в), при c = 1. Шкала показывает 1 мм

Рис. 4. Интенсивность в начальной плоскости (a), полученная через произведение функций Бесселя, а также интенсивности (б, в) на расстоянии z = z 0 / 10, полученные через преобразование Френеля (б) и через ряд (19) квадратичных пучков Бесселя–Гаусса (в), при c = 1,5.

Шкала показывает 1 мм

Рис. 5. Интенсивность в начальной плоскости (a), полученная через произведение функций Бесселя, а также интенсивности (б, в) на расстоянии z = z 0 / 10, полученные через преобразование Френеля (б) и через ряд (19) квадратичных пучков Бесселя–Гаусса (в), при c = 2. Шкала показывает 1 мм

На рис. 6 показаны распределения фаз в начальной плоскости для пучков на рис. 3 – 5. На рис. 6 а показана фаза для пучка с c = 1 (рис. 3 а ), на рис. 6 б показана фаза для пучка с c = 1,5 (рис. 4 а ) и на рис. 6 в показана фаза для пучка с c = 2 (рис. 5 а ). Из рис. 6 видно, что, как и предсказывает теория на декартовых осях, корни (нули интенсивности) будут с ростом параметра c удаляться от центра (19), а корни, лежащие на диагоналях, будут приближаться к центру (17). При этом первое кольцо на рис. 6 а имеет вид квадрата с выгнутыми наружу сторонами, а это же первое кольцо на рис. 6 в имеет вид квадрата с вогнутыми внутрь сторонами (подушка). В центре пучка (на оптической оси) находится оптический вихрь с топологическим зарядом n =4.

Рис. 6. Распределения фаз в начальной плоскости пучков, показанных на рис. 3а – 5а, у которых параметр с был равен: 1 (а); 1,5 (б); 2 (в). Шкала показывает 1 мм

Из рис. 3 – 5 видно, что при распространении ББГ2-пучки не вращаются и слабо изменяют вид распределения интенсивности. Хотя структурностабильными такие пучки назвать нельзя, так как в дальней зоне эти пучки будут иметь вид распределения интенсивности в виде концентрических световых колец. Это видно из ряда в (15). Так как все пучки Бесселя в ряде будут расходиться тем быстрее, чем больше их топологический заряд, при этом амплитуды этих пучков (весовые коэффициенты ряда в (15)) будут убывать с ростом топологического заряда, то есть самое яркое кольцо в дальней зоне будет у пучка Бесселя с топологическим зарядом n , который описывается первым слагаемым в ряде (15). На рис. 7 показана интенсивность ББГ2-пучка (15) на расстоянии половины длины Рэлея ( z = z 0 /2) при c = 1. Видно, что уже на этом расстоянии пучок в виде сглаженного квадрата (рис. 3) превратился в кольцевой пучок, окруженный боковыми кольцами.

Рис. 7. Интенсивность пучка (15) на расстоянии z = z 0 / 2 от перетяжки при c = 1. Размер кадра – 10×10 мм

Оценим расходимость пучка (15). Пучок Бесселя– Гаусса с квадратичным аргументом и топологическим зарядом n , который является первым членом ряда в (15), имеет начальный радиус, как и у обычных пучков Бесселя-Гаусса, r ₀ - w ₀ V n /2 . Пучок Бесселя–Гаусса с квадратичным аргументом β r ² распространяется, как после сферической линзы с фокусным расстоянием f = k / (2β). То есть он расходится после прохождения фокуса, и на расстоянии z = z 0 / 10 его радиус r z увеличится по сравнению с начальным радиусом r 0 в число раз, равное отношению ( z 0 / 10– f )/ f . Таким образом, получим оценку величины расходимости пучка (15), как отношение радиусов:

r z = -*- - 1 = W L1=« kw i - 1 „ 14 r 0 10 f 10        10⁷

Последнее значение немного больше, чем получено при моделировании (13,6 – 13,9).

• 6.    Моделирование распространения ББГ-пучков второго типа

Параметры моделирования пучка (21): длина волны λ =532 нм, радиус перетяжки w 0 = 1 мм, топологический заряд n =4, масштабирующий множитель пучков ББГ-пучка α = k /200, параметр асимметрии c = 1, расстояния распространения z =0, 0,1 z 0 , 0,2 z 0 . Полуразмер расчётной области R = 10 мм. На рис. 8 показаны распределения интенсивности на разных расстояниях от начальной плоскости. На рис. 8 а показана увеличенная в 10 раз картина интенсивности пучка в начальной плоскости, а на рис. 8 в , г показаны интенсивности этого пучка на расстояниях 0,1 z 0 ( в ), 0,2 z 0 ( г ).

Из сравнения интенсивностей на рис. 8 видно, что при распространении пучок увеличился в размере, повернулся на 90 градусов и «потерял» боковые кольца. Для обычного пучка Бесселя известно, что интенсивность в дальнем поле имеет вид кольца без боковых лепестков. Для пучка Бесселя–Гаусса то же в дальнем поле формируется уширенное светлое кольцо. Если есть осевая суперпозиция пучков Бесселя– Гаусса разного порядка, то все они в дальнем поле формируют одно кольцо с распределением интенсивности вдоль этого кольца, которое зависит от весовых коэффициентов в сумме (21). Если в начальной плоскости данная суперпозиция имеет максимум с центром на горизонтальной оси, как на рис. 8 а , то в дальнем поле центр максимальной интенсивности должен быть на вертикальной оси, как на рис.8 б , в . То есть интенсивность должна повернуться на 90 градусов. Это следует из того, что у каждой функции Бесселя в ряде (21) в дальнем поле в аргументе появится мнимая единица c минусом, так как аргумент комплексной величины q ( z ) (фаза Гоу) равен π /2. Поэтому для каждой функции Бесселя в дальнем поле получим: J n ( - ix ) = ( - i ) I n ( x ) , где I n ( x ) - модифицированная функция Бесселя. Тогда в сумме (21) вместо коэффициентов ( c exp( i ф )) l + ⁿ получим ( c exp( i ( ф - п / 2) )) l + ⁿ . То есть вид распределения интенсивности вдоль кольца в дальней зоне не изменится, если повернуть начальную картину на 90 градусов против часовой стрелки. Оценим расходимость пучка (21). Заметим, что дальняя зона для пучка Бесселя–Гаусса наступает не так, как для гауссова пучка, при z >  z 0 , а раньше, при z >  z 1 = wk / α. Так как α = k / 200, то z 1 = 200 w =200 мм. А расстояние Рэлея для случая на рис. 8 равно z 0 = kw ² /2~6000 мм. То есть уже на расстоянии 0,1 z 0 =600 мм (рис. 8 в , г ) для пучков Бесселя (21) будет дальнее поле. Радиус кольца (полумесяца) R 1 на рис. 8 в можно оценить, исходя из выражения R 1 ~ z tgθ, где θ – угол наклона конических лучей, формирующих пучки Бесселя в ряде (21). И так как tgθ ~ sinθ = α / k , то R 1 = z α / k =( z 0 / 10) /200 =3 мм. Точный расчет показал, что расстояние от оптической оси до центра полумесяца на рис. 8 в равно 2,874 мм.

Рис. 8. Распределение интенсивности ББГ- пучка (21) при разных z: 0 (а), 0,1z 0 (в), 0,2z 0 (г) и фаза в начальной плоскости (б) . Шкала показывает 1 мм

На рис. 9 показана интенсивность пучка ББГ второго типа (21) на расстоянии z = 0,04 z 0 . Особенность этого распределения интенсивности в том, что на нем видны два типа пучков разного масштаба. В центре видно малое распределение интенсивности в виде полумесяца, центр которого лежит на горизонтальной оси, и неоднородное кольцо много большего диаметра, такой же полумесяц, центр которого лежит на вертикальной оси. Наличие в одном пучке на рис. 9 двух пучков разного масштаба можно объяснить исходя из природы пучка Бесселя–Гаусса. Гауссов пучок, как мягкая диафрагма, ограничивает апертуру пучка Бесселя. Поэтому пучок Бесселя распространяется почти бездифракционно, сохраняя свой начальный размер, примерно до расстояния z 1 = wk / α. Этот бездифракционный пучок формируется с помощью конического волнового фронта, и на расстоянии z =0,04 z 0 =240 мм к оптической оси будут приходить лучи от «края начальной апертуры» (с расстояния, равного радиусу перетяжки w ). А те лучи, которые пересекли оптическую ось на более близком расстоянии, расходятся и формируют на расстоянии z = 0,04 z 0 другой тип пучка, а именно, пучок в дальнем поле (полумесяц без боковых лепестков и повернутый на 90 градусов, как на рис. 9). При дальнейшем распространении без-дифракционная часть пучка пропадает и остается только часть пучка в дальнем поле, как на рис. 8 в , г . Размер бездифракционной части пучка (21), равный размеру пучка в начальной плоскости (рис. 8 а ), можно оценить с помощью половины расстояния до первого нуля функции Бесселя 4-го порядка. Корень функции Бесселя 4-го порядка примерно равен 7,3, поэтому расстояние до полумесяца на рис. 8 а будет примерно равно r =3,6/ α = 3,6×200 / k =61 мкм. Точное расстояние равно 88 мкм.

Заключение

Рассмотренные ББГ-пучки можно сформировать с помощью фазового модулятора света с использованием известных методов кодирования амплитуднофазовой функции (3) в только фазовую функцию. Аномально быстрый поворот интенсивности, состоящей из двух лепестков, можно использовать для уве- личения продольного разрешения оптического микроскопа, так как смещение источника света вдоль оптической оси будет приводить к поперечному повороту двух лепестков интенсивности. Чем выше скорость поворота двух лепестков интенсивности, тем выше продольное разрешение оптического микроскопа. Пучок с двумя лепестками в виде двух «месяцев» можно использовать для оптического захвата биологических клеток по их краям и перемещать их, чтобы не повредить мощным излучением в центре гауссова пучка. Плавно меняя параметр c пучка, можно растягивать клетки, так как с увеличением параметра с увеличивается не только ТЗ пучка, но и расстояние между двумя лепестками интенсивности.

Рис. 9. Распределение интенсивности ББГ-пучка (21) на расстоянии z = 0,04z 0 . Размер кадра – 6×6 мм

Работа выполнена при поддержке Российского научного фонда, грант 22-12-00236 в частях теории и при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию НИЦ «Курчатовский институт» в части моделирования.