Вихревые моды Айнса–Гаусса как суперпозиции мод Эрмита–Гаусса

Известно, что моды Айнса–Гаусса (АГ) [1 – 3] вещественны и поэтому не являются вихревыми пучками и не несут орбитальный угловой момент (ОУМ). В работах [3, 4] был рассмотрен вариант вихревых (helical) мод АГ (вАГ) hIG p,q ( x, y , ε), где p и q – неотрицательные целые числа, а ε – вещественное число (параметр эллиптичности) как осевая суперпозиция чётных и нёчетных нормированных мод АГ с задержкой по фазе на π / 2. В [4] численно показано, что ОУМ таких вихревых мод зависит от параметра эллиптичности ε. Однако аналитически зависимость ОУМ от ε не была получена. Также не рассматривался вопрос о величине топологического заряда (ТЗ) вАГ-мод. Сохраняется топологический заряд при изменении параметра ε или нет? В работе [5] была предпринята попытка представить моды АГ как суперпозицию мод Ла-герра–Гаусса (ЛГ), но явный вид коэффициентов разложения не был найден. Хотя в [5] и не получили аналитических выражений коэффициентов разложения АГ по модам ЛГ, но представили подробный алгоритм их расчета и на множестве примеров дали пояснение с геометрическим отображением мод АГ на сферу в сообществе с ЭГ- и ЛГ-пучками. В [6] мы привели явный вид коэффициентов разложения мод АГ по модам Эрмита–Гаусса (ЭГ) и ЛГ для случаев, когда p ≤ 6.

Вихревые моды АГ, как и невихревые, достаточно широко применяются в оптике. В [7] изучались поляризационные структуры пучков АГ. Среди различных способов экспериментальной реализации мод АГ отметим следующие: c помощью элемента с метаповерхностью [8], динамическим способом с помощью управляемого от компьютера адаптивного зеркала с большим числом микроячеек [9], с помощью спонтанной параметрической конверсии [10]. В последнем случае были сформированы двухфотонные перепутанные вихревые моды АГ, которые применяются в квантовой информатике [4]. Вихревые моды АГ можно получать с помощью призмы Дове и интерферометра Маха–Цандера [11], в резонаторе лазера на чипе с диодной накачкой [12] и в других типах лазеров [13]. Пучки АГ можно также генерировать как вторые гармоники при нелинейном преобразовании в кристалле [14]. В работе [15] было реализовано классическое перепутывание мод АГ. Фактически в этой работе были рассмотрены пучки Пуанкаре, но не на основе мод ЛГ, а на основе мод АГ. Прохождение мод АГ через турбулентную атмосферу изучалось в [16]. Моды АГ применяются не только в квантовой информатике и для зондирования атмосферы, но и для манипулирования микрочастицами [17]. Моды АГ продемонстрировали множество интересных свойств при распространении в различных типах сред, например, в сильно нелокальных нелинейных средах [18], в маломодовых волокнах с эллиптической сердцевиной

• [19] . Моды АГ применялись также для эффективного взаимодействия атомов друг с другом [20].

Для полноты картины заметим, что пучки АГ похожи (и по свойствам, и визуально по структуре распределения интенсивности) на пучки Эрмита– Лагерра–Гаусса [21 – 24], которые также зависят от некоторого вещественного параметра (степень астигматизма) и при его изменении преобразуются из пучков ЭГ в пучки ЛГ. В [25] теоретически, геометрически и экспериментально была показана связь между модами Эрмита–Лагерра–Гаусса и модами АГ.

Интересно, что, хотя вихревые моды АГ давно применяются в оптике, многие теоретические вопросы остаются до сих пор не выясненными. Неизвестно, зависит топологический заряд вихревых мод АГ от параметра эллиптичности ε или нет? Обладает ли в общем случае ОУМ мод АГ какой-то симметрией в зависимости от ε или нет? Почему для одних номеров q ОУМ увеличивается с ростом ε, а для других q уменьшается? В данной работе мы попытались ответить на некоторые из указанных вопросов. Мы получили конкретные выражения для ОУМ некоторых вихревых мод АГ с зависимостью от параметра ε, которые можно проанализировать до моделирования. Причина, почему удается найти точные аналитические выражения только для номеров p мод АГ меньше 5, в том, что уравнения для нахождения собственных чисел для этих номеров являются квадратными или кубическими. Для номеров p > 5 это уравнения четвертой степени и выше, которые нельзя решить аналитически. Мы доказали также, что ОУМ любой моды АГ является чётной функцией от ε, и показали, что ТЗ при ε = 0 может отличаться от ТЗ при ε = ∞.

1. Нормированные невихревые моды Айнса–Гаусса

Моды Айнса–Гаусса [1 – 3] являются структурно устойчивыми решениями параксиального уравнения Гельмгольца { 5 2 + 5 2 + 4 i d z } F ( r , z ) = 0 , разделяющимися в параболических координатах ( ^ , п ), и имеют вид:

p /2

IG p,q ( r , z ) = G ( r , z ) I— i -l X l 1 + iz J

X Np, q (i ^, e) Np, q (П, e), где r =(x, y) – двумерный вектор,

^{G ( r} , ^z ) = 7-¹-^exP

1 + iz

r ² I

1 + iz J

– стандартное гауссово решение параксиального уравнения и N(t)= Np,q(t, e) - тригонометрический многочлен Айнса. Здесь и далее мы рассматриваем все световые поля в безразмерных переменных. Переход к размерным переменным осуществляется заменой x := x/w0 , y := y/w0, z := 2z/(kw2), где w0 -радиус перетяжки гауссова пучка. Кроме того, мы будем записывать моды ЭГ, ЛГ и АГ в нормированном варианте (используя жирный шрифт) и без нормировки (используя курсив). В частности,

IG %q ) ( r , e ) =

IG Peqo ) ( r , e ) || IGPeqo ⁾ ( r , e)||^.

Верхний индекс ( e или o ) означает, что рассматривается чётная или нечётная мода АГ. Параметр ε (параметр эллиптичности) является вещественным. Его изменение в пределах от –∞ до +∞ позволяет изменять распределение интенсивности моды АГ.

Напомним выражения для мод ЭГ и ЛГ через многочлены Эрмита и Лагерра соответственно:

. X ( n + m )/2

HGn, m (r, z) = G (r, z )|------I l1 + iz J

X H n

,

/       \ n + m /2

I 1 — ZZ 1

LGn ,± m (r, z) = G (r, z )|------I l1 + iz J

2 r ²

X L m ------- r ^m e ± ^im ■.

1 1 + z ² J

HG n , m ( r )

G ⁿ , m ⁽⁾ || HG . , m ( r )||’

||HG. , m ( r )|| =

LG . ,± m ( r ) =

n

J— ■ 2 ^{n + m} . ! m !,

LG . ,± m ( r )

II LG . , ± m ( r )ll’

I LG.. m ( r )|| =П • ( l if

.

Хорошо известно и следует из формул (3), что индексы n, m мод ЭГ – это число горизонтальных и вертикальных нулевых линий интенсивности, а радиальный и азимутальный индексы n, ±m мод ЛГ – это число нулевых колец интенсивности и топологический заряд оптического вихря в центре. Для мод АГ индексы p, q также определяются через число нулевых линий интенсивности – незамкнутых (гипербол и прямых, это индекс q) и замкнутых (эллипсов, это (p – q) / 2), причём наличие нулевой линии y = 0 однозначно указывает, что это нечётная мода АГ. К сожалению, Эдвард Айнс, изучая в 1920-е годы тригонометрические многочлены Np,q(t, e), рассматривал их как вещественные линейные комбинации косинусов или синусов кратных углов, cos kt или sin kt. Исследовал он их по отдельности, обозначая как C(pq)(t,e) и Spq)(t,e), где 0 < q < p и индекс q имеет ту же чётность, что и p, т.е. q€{p, p - 2, p -4, ...}. Если бы многочлены Np,q(t, e) рассматривались как линейные комбинации комплексных экспонент eikt, то всё исследова- ние можно было бы провести в едином стиле. При этом индекс q пробегал бы все целочисленные значения от 0 до p. Тем не менее, далее мы будем придерживаться уже устоявшихся обозначений.

В предельных случаях s = 0 и s = ±¥ моды АГ сводятся к модам ЛГ и ЭГ. Если s = 0, то

IG p , q ( r ,0) = <2 Re LG _{( p} — q _V2, q ( r ),

IG P , ( r ,0) = ^Im LG ( p — q )_/2, q ( r ),

за исключением случая (p , q ) = (2 n , 0), когда IG 2 _n ,₀ ( r ,0) = LG _n ,₀ ( r ), а нечётной моды АГ просто нет. Если s = +¥, то

IG 2 3 ( r , s ) = + b ^HG 3.0 ( r )-j • ^HG 1^,2 ^{( r )} = ■                     4 3 + b ²

= ( b + 3)Re LG 0,3 ( r ) - Л( b - 1)Re LG 1,1 ( r ) 2z • 4 3 + b ²

o        ₊ c • HG 2,1 ( r ) - Л • HG 0,3 ( r )_

'G       ^{s )} ■                   . .

= 2$(,c + 1) Im LG 0,3 ( r ) - ( c - 3) Im LG 1,1 ( r )

22 • 4 3 + c ^{2                :}

IG ²p , q ( r , +» ) = ( — 1) ⁽ p - q V² HG q , p — q ( r ), IG “p , q ( r , +« ) = ( — 1) ⁽ p — q V² HG q —1, p +1— q ( r ).

Если s = -¥, то

IG ²p , q ( r , -» ) =

J( - 1) p /² HG p - q , q ( r ), p = 2 k ,

[ ( - 1) ⁽ p HG p +1- q , q -1 ( r ), p = 2 k + 1, IG “p , q ( r , -» ) =

Г ( — 1) p /^{2 + 1} HG p +1- q , q —1 ( r ), p = 2 k , [ ( — 1) ⁽ p -R² HG p - q , q ( r ), p = 2 k + 1.

Для промежуточных значений e моды АГ сводятся уже не к одной моде ЛГ или ЭГ, а к суперпозиции таких мод. Если выбран базис мод ЛГ, то IG p , _q ( r , s ) и IG o_p , _q ( r , s ) разлагаются соответственно по Re- и Im-частям мод LG _k , _{p - 2 k} ( r ), где индекс суммирования k пробегает значения от 0 до [ p /2j . Если выбран базис мод ЭГ, то IG p , _q ( r , s ) и IG p , _q ( r , s ) разлагаются по модам HG _p - _k , _k ( r ), где 0 <  k <  p , но для чётных мод АГ индекс суммирования k пробегает только чётные значения, а для нечётных мод АГ - только нечётные.

В работе [26] мы нашли такие разложения для случаев p <  6. Например, для чётных и нечётных мод АГ с индексами ( p , q ) = { (2,2), (3,1), (3,3) } формулы следующие:

a • ^HG 2,0 ^{( r ) - HG} 0,2 ^{( r )}

2+22      ’          (8)

IG ^( r , s ) = HG 1,1 ( r ).

IG 2 ,1 ( r , s ) =

Л • HG 3,0 ( r ) + b • HG 1,2 ( r )

4 3 + b ²

V3( b - 1) Re LG o,3 ( r ) + ( b + 3) Re LG 1,1 ( r )

IG O ,1 ( r , s )

22 • 4 3 + b ²

Л • HG 2,1 ( r ) + c • HG 0,3 ( r )

4 3 + c ²

(£ -32Im LGo^r ) + V3( c + l)Im LG 1^ r )

44. • 4 3 + c ²

где a = a (s) = s + 4 s2 +1, b = b (s) = s -1 + 2 (s-1)2 + 3, c = c (s) = s + 1 + 4 (s +1)2 + 3.

Используя равенства a ( s ) a (- s ) = 1 и b ( s ) c (- s ) = 3, легко проверить свойства симметрии мод АГ (8) -(12) при изменении знака параметра эллиптичности:

IG 2 n ,2 m ( x , y , -s ) = ( - 1) m IG 2 n ,2 m ( У , X , s ),

IG On ,2 m ( x , y , -s ) = ( - 1) m ^{+ 1} IG On ,2 m ( У , X , s ),          (14)

IG On +1,2 m +1 ( x , y , -s ) = ( - 1) m IG 2 n +1,2 m +1 ( У , X , s ).

Можно доказать, что эти свойства сохраняются и для общего случая индексов (p, q ). Моды АГ не являются вихревыми модами и не обладают орбитальным угловым моментом (ОУМ). Далее, на основе разложений (8) - (12) и аналогичных разложений с другими индексами (p, q ), мы получим выражения для амплитуд вихревых мод АГ (вАГ).

2. Разложение вихревых мод АГ по модам ЭГ

Следуя работам [3, 4], будем строить вАГ-моды (helical Ince-Gaussian modes, hIG modes) как суперпозицию нормированных чётной и нечётной мод АГ, сдвинутых по фазе на п /2:

hIG ±, q ( r , s )

IG p , q ( r , s ) ± i IG p , q ( r , s )

2i

Очевидно, что, не изменяя общности, достаточно рассмотреть только случай вАГ-мод, у которых между компонентами стоит знак ‘+‘. Для индексов ( p , q )= {(2, 2), (3, 1), (3, 3)}, в силу формул (8)-(12), вАГ-моды принимают вид

hIG +,2 ( r , s ) =

hIG +,1 ( r , s ) =

IG 2,2 ( r , s ) + i IG ^O 2,2 ( r , s )

2i

1 f a • HG 2,0 ( r ) - HG 1,2 ( r )

22 [        2 1 + a ²

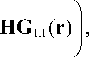
IG 2 ,1 ( r , s ) + i IG O ,1 ( r , s )

1 f 23 • HG 3,0 ( r ) + b • HG 1,2 ( r )

22 [         2 3 + b ²

H • HG 2,1 ( r ) + c • HG o,3 ( r ) ] + i

2+42       J

hIG +,з ( г , s ) =

IG^ ( r , £ ) + i IG o ,3 ( r , £ )

1 f b ■ HG 3,o ( r ) - Л • HG 1,2 ( r )

4 3 + b ²

c HG 2,1 ( r ) - Л ■ HG 0,3 ( r ) ]

+ ¹---------------- 1        --------------

4 +cs       J

hIG +, q ( r ,0) = LG ( p - q)/2,q ( r ), ( p - q ^)/2

hIG + , q ( r , +« ) = ⁽          X

X{HGq,p-q (r) + iHGq-1,p+1-q (r)}, hIG+p,q (r, -*) =

= ^ { HG p +1- q , q -1 ( r ) + i HG p - q , q ( r ) } .

Так как рассматриваемые пучки структурно устойчивы (моды), то при распространении в свободном пространстве они сохраняют форму поперечного распределения своей интенсивности, изменяясь только в масштабе.

3.    Орбитальный угловой момент вихревых мод АГ

Разложение вАГ-мод по модам ЭГ позволяет найти орбитальный угловой момент (ОУМ, orbital angular momentum, OAM) этих пучков для любого параметра ε. Известно [27], что для любого структурно устойчивого поля, заданного в плоскости перетяжки разложением по базису мод ЭГ:

E ( r ) = ^ C m HG N - m , m ( r ) ,

0< m < N его ОУМ вычисляется по формуле

2 £ Im( C m -1 C m )( N + 1 - m )! m !

OAM [ E ( r ) ] = 1 < ^m < ^N -----------------. (19)

^{L J} £ | C m |²( N - m )! m !

0< m <  N

Если перейти к нормированным полям,

E ( r ) = £ C m HG N - m,m ( r ) ,

0< m < N то формула (19) преобразуется следующим образом:

OAM [ E ( r ) ] = 2 £ Im( C m -1 C m )J( N + 1 - m ) m . (20) 1< m <  N

Применяя формулу (20) для вАГ-мод (16) – (18), получаем

OAM [ hIG +,2 ( r , s ) ] = ^{(1 +}a^ , 4 1 + a ²

OAM [hIG +,, ( r , s ) ]= (3 - 2' + bc)4 ,         (21)

4 (3 + ь ² )(3 + c ² )

i        (3 + 2 c + bc )43

OAM [ hIG +, 3 ( r , s ) l =                  ,

^{L ]}      (3 + b ² )(3 + c ² )

где параметры a , b , c задаются формулами (13).

Для предельных случаев параметра эллиптичности ( s = 0 и s =±¥) вАГ-моды сводятся соответственно к одной стандартной моде ЛГ и к комплексной сумме двух мод ЭГ, благодаря соотношениям (5) – (7):

Для ε =0 ОУМ вАГ-моды равен топологическому заряду моды ЛГ: OAM = q . Для случаев s =±¥ также всё просто, т.к. в сумме (20) остаётся только одно слагаемое: m = p +1- q для s = +¥ и m = q для s = -¥. Итак, для пучков (22) получаем:

OAM [ hIG +, q ( r ,0) ] = q ,

OAM [ hIG +, q ( r , ±® ) ] = 4 q ( p + 1 - q ).

В частности, из (23) следует, что ОУМ вАГ-мод с индексами p = 7 и q = 1, 3, 5, 7 при s = 0 равен соответственно 1, 3, 5, 7, а при s = ±® ОУМ этих же мод равен соответственно 7, 15, 15, 7 . Поэтому кривая зависимости ОУМ от е для моды с q = 7 должна дважды (при s >  0 и при s <  0) пересекать аналогичные кривые ОУМ для q = 3 и 5. Ранее этот результат был получен численно в работе [4]. Тем самым формулы (23) служат теоретическим обоснованием и обобщением численного результата из работы [4].

Нетрудно также проверить согласие формул (21) с общими результатами (23), подставляя в (21) значения a (0) = 1, b (0) = 1, c (0) = 3 и асимптотики a ( s ) ~ 2 s , b ( s ) ~ 2 s , c ( s ) ~ 2 s при s ^ +® .

Выражения (21) – (23) являются одним из основных результатов данной работы, так как аналитически выражают зависимость ОУМ вихревых пучков АГ при некоторых первых индексах ( p, q ) и любом вещественном параметре ε. Понятно, что аналогично с помощью метода, изложенного в [26], можно получить выражения для ОУМ других вихревых мод АГ ( p >3), но эти выражения с увеличением p будут становиться всё более громоздкими. В Приложении А мы приведём без доказательства выражения для ОУМ вихревых мод АГ при p = 4 и 5.

4.    Топологический заряд вихревых мод Айнса–Гаусса

На основе разложения пучков АГ по модам ЛГ (9)– (12) и других из [27] можно определить топологический заряд (ТЗ, topological charge, TC) вихревых мод АГ при ε =0, TC = q . Для вАГ-мод (16) – (18) этот результат можно проверить непосредственно, полагая ε = 0 и переходя к модам ЛГ на основе формул (9) – (12).

Интересно выяснить, меняется ли ТЗ вАГ мод при изменении параметра ε? Из (22) видно, что при ε =+¥ любая вАГ-мода является суперпозицией двух мод ЭГ. Поэтому, в силу (3), её нулями являются нули многочлена от двух переменных:

H q ( X ) H p - q (Y ) + i ■ H q —1 ( X ) H p _{+ 1}- q ( Y ) ,           (24)

где для краткости мы сделали замену X = x V2 , Y = y V2 . Сумма (24) зануляется в двух случаях:

• 1)    H q ( X ) = H p +1- q (Y ) = 0,

• 2)    H q -1 ( X ) = H p - q ( Y ) = 0.

Поскольку многочлен Эрмита H n ( t ) имеет n простых (невырожденных) вещественных нулей (обозначим их как t n,k , где k = 1, 2, …, n ), то в первом случае мы имеем набор из q ( p + 1 – q ) изолированных нулей ( X 0 , Y >) = ( t q ,v , t p +1- q, ^ ), где о <  V <  q и о <Ц< p + 1 - q , а во втором случе - набор из ( q - 1)( p - q ) изолированных нулей ( X о , Y o ) = ( t q -1, _v , t p - q ,ц ), где 0 < v <  q - 1 и 0 <ц< p - q . Можно показать, что все нули в первом случае относятся к нулям типа ( X + iY ), т.е. имеют ТЗ, равный + 1, а все нули во втором случае – к нулям типа ( X - iY ), т.е. имеют ТЗ, равный -1. Действительно, используя свойства H ( t ) = 2 nH n -1 ( t ) и H _{n + 1} ( t ) = 2 tH n ( t ) - 2 nH n -1 ( t ), легко заметить, что при фиксированных пик выражения H _n -1 ( t _n , k ), H n _{+ 1} ( t n , k ) и H ‘ ( t _n , k ) отличны от нуля, причём H n -1 ( t n , к ) и H n ( t n , _к ) - одного знака, а H n ₊ 1 ( t n , к ) и H ‘ ( t _n , _к ) — разных знаков. Поэтому, разлагая сумму (24) в ряд Тейлора до линейных членов в окрестности каждого изолированного нуля ( X ₀ , Y ₀ ), мы получим, что в первом случае коэффициенты при ( X - X ₀ ) и i ( Y - Y ₀ ) будут одного знака, и во втором случае коэффициенты при ( Y - Y 0 ) и i ( X - X ₀ ) будут одного знака. Тем самым, ТЗ моды hIG +, _q при е = +® равен q ( p + 1 - q ) - ( q - 1)( p - q ) = p . При е = -да ТЗ находится аналогично и тоже равен p .

Таким образом, для мод hIG+,q при q = p ТЗ не зависит от параметра е, но для мод с q < p ТЗ будет увеличиваться с ростом |е| от q при е = 0 до p при е = ±да. То, что ТЗ увеличивается при увеличении |е|, не должно быть сюрпризом. Например, разложение hIG+,1 по модам ЛГ, hIG+,1(r, е) =

_ V3( b - 1)Re LG 0,3 ( r ) + ( b + 3)Re LG 1,1 ( r )

=              2^37#                 (5)

. ( c - 3)Im LG 0,3 ( r ) + V3( c + 1)Im LG 1,1 ( r )

+i ^                                     3 c                                  ’ показывает, что при стремлении к бесконечности и радиальной переменной r, и параметра ε, без учета общей гауссовой составляющей, вместо (25), получается выражение, зависящее только от азимутального угла ф:

^hIG + ,1 ⁽ r , + ^{да )}| r    -

~ (V3 cos3 ф + i sin 3 ф ) + (cos ф + i V3 sin ф ).

Cогласно [28], ТЗ суммы двух оптических вихрей с разными коэффициентами равен ТЗ оптического вихря с бóльшим коэффициентом, а если коэффициенты равны, то большему ТЗ в суперпозиции. Поэтому ТЗ моды (26) равен 3, хотя при ε =0 он был равен 1.

5.    Четность функции ОУМ по параметру ε

Из определения вАГ-моды (15) следует, что из-за вещественности чётной и нечётной мод АГ смена знака топологии вихревой моды приводит к комплексному сопряжению моды. В силу этого, при смене знака топологии ОУМ тоже поменяет знак:

OAM [ hIG -, _q ( r , е ) ] = - OAM [ hIG +, _q ( r , е ) ] . (27)

С другой стороны, из (14) видно, что при смене знака у параметра ε, вАГ-мода становится сопряжённой, а декартовы координаты меняются местами:

hIG ±, q ( x , y , -е ) = ( - 1) m x

[ hIG J , q ( y , x , е ), (p , q ) = (2 n , 2 m ), (28) x^

[± i ■ hIG J , _q ( y , x , е ), (p , q ) = (2 n + 1,2 m + 1).

Перестановка переменных x и y приводит к изменению знака оператора поворота x д y - y д _x , а замена е на -е приводит к сопряжению вАГ-моды. Поэтому ОУМ исходной вАГ-моды при замене е на -е останется прежним. То есть ОУМ любой вАГ-моды является чётной функцией параметра ε:

OAM [ hIG +, _q ( r , -е ) ] = OAM [ hIG +, _q ( r , е ) ] . (29)

Интересно выяснить, будет ли ОАМ вАГ-мод достигать максимума при ε = 0? Для этого есть некоторые основания, т.к. при ε = 0 любая вАГ-мода сводится к некоторой моде ЛГ (22). Причем при ε > 0 в разложении вАГ-моды всегда есть несколько мод ЛГ с разными ТЗ, что должно приводить к уменьшению ОУМ из-за перераспределения между несколькими модами. Из (23) следует, что при q <  ( p + 1)/2 ОУМ на бесконечности, е = ±да , будет больше, чем ОУМ при ε = 0, и, наоборот, при q >  ( p + 1)/2 ОУМ на бесконечности будет меньше, чем при нулевом ε.

6.    Моделирование

На рис. 1 показаны распределения интенсивности для вАГ-мод, рассчитанных по формуле (15) для индексов p =7 и q = 1, 3, 5, 7. Легко заметить симметрию интенсивностей для случаев ε и – ε (одна интенсивность превращается в другую при отражении относительно прямой y = x ), которая следует из формул (14).

На рис. 2 показаны распределения интенсивности (верхняя строка) и фазы (нижняя строка) для вАГ-мод hIG +, _q ( r , +да ) для индексов q =1, 3, 5, 7. Расчет проводился по формуле (22). Радиус перетяжки – 1 мм, размер кадров – R ≤ x, y ≤ R , где R = 10 мм. Топологический заряд мод на рис. 2 рассчитывался численно по формуле М. Берри [29]:

TC [ E ( r , ф ) ] = —limIm    —- ’ ^ d ф ,

2 n r -“ 0 E ( r , ф )

где E ( r , φ) – комплексная амплитуда вАГ-моды в плоскости перетяжки в полярных координатах. В численных расчётах радиус окружности, по которой мы вычисляли ТЗ, выбирался равным половине длины стороны кадра на рис. 2. Расчёт ТЗ для разных индексов q привёл к следующим результатам:

TC = 6,9966237 ( q = 1), TC = 6,9973487 ( q = 3), TC = 6,9973487 ( q = 5), TC = 6,9966237 ( q = 7). То есть ТЗ для всех q получался равным p =7, что и предсказывает теория. Из распределения фаз на рис. 2 можно найти 7 линий скачков фазы на 2π, у которых есть начальные точки, расположенные на вертикальной оси ( q = 1), на горизонтальной оси ( q = 7 ) или на двух вертикальных ( q = 3 ) и двух горизонтальных линиях ( q = 5).

–80 –10      –5        –2        –1 ε =0        1         2         5         10        80

Рис. 1. Распределение интенсивности в перетяжке вАГ-мод (15) p = 7 и q = 1, 3, 5, 7(сверху вниз) и некоторых значениях параметра ε

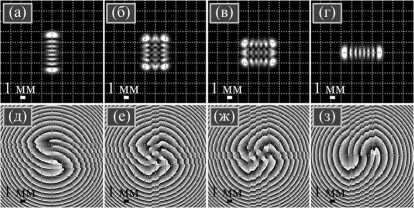
Рис. 2. Интенсивность (сверху) и фаза (снизу) для вихревых мод АГ в начальной плоскости при ε = +∞ для номеров p = 7, q: 1 (первый столбец), 3 (второй столбец), 5 (третий столбец) и 7 (четвертый столбец)

На рис. 3–5 показаны интенсивности и фазы мод вАГ в начальной плоскости для индексов ( p , q )=(2,2), (3,1) и (3,3) при разных значениях параметра ε. Радиус перетяжки гауссова пучка w 0 = 1 мм, размер кадра – R ≤ x, y ≤ R =3 мм.

Для распределений из рис. 3–5 рассчитывался ОУМ, нормированный на мощность пучка. Для расчёта использовалось выражение через двойной интеграл по всей поперечной плоскости:

J z W

Im j J E * ( r , ф) — E ( r , ф ) rdrd ф

О О          дФ_______________ jj E * (r, ф) —(r, ф) rdrd ф

^J0 0            ^дф

.

Для полей с рис. 3 численно рассчитанные значения ОУМ составили 1,449085 (ε = –20), 1,622474 (ε =– 3), 1,847747 (ε =–1), 1,999962 (ε =0), 1,847747 (ε = 1), 1,622474 (ε =3), 1,449085 (ε = 20). Соответствующие теоретические значения, полученные по формуле (21), равны 1,449095 (ε =–20), 1,622484 (ε =–3), 1,847759 (ε =–1), 2,000000 (ε =0), 1,847759 (ε = 1), 1,622484 (ε =3), 1,449095 (ε =20).

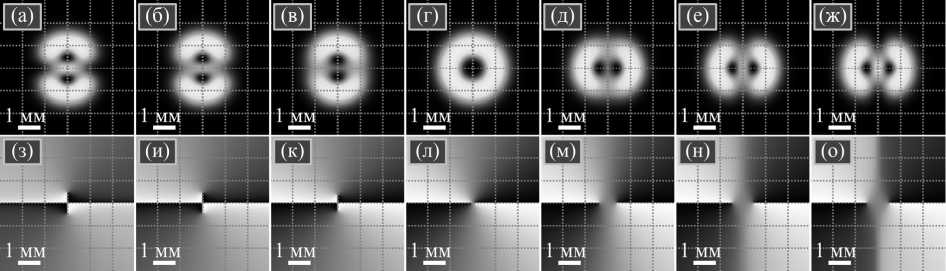
Рис. 3. Распределения интенсивности (а-ж) (чёрный цвет – ноль, белый цвет – максимум) и фазы (з-о) (чёрный цвет – 0, белый цвет – 2π) моды вАГ при (p, q) = (2, 2) для ε = –20 (а, з), –3 (б, и), –1 (в, к), 0 (г, л), 1 (д, м), 3 (е, н), 20 (ж, о)

Рис. 4. Распределения интенсивности (а – ж) (чёрный цвет – ноль, белый цвет – максимум) и фазы (з – о) (чёрный цвет – 0, белый цвет – 2π) моды вАГ при (p, q) = (3, 1) для ε = –20 (а, з), –3 (б, и), –1 (в, к), 0 (г, л), 1 (д, м), 3 (е, н), 20 (ж, о)

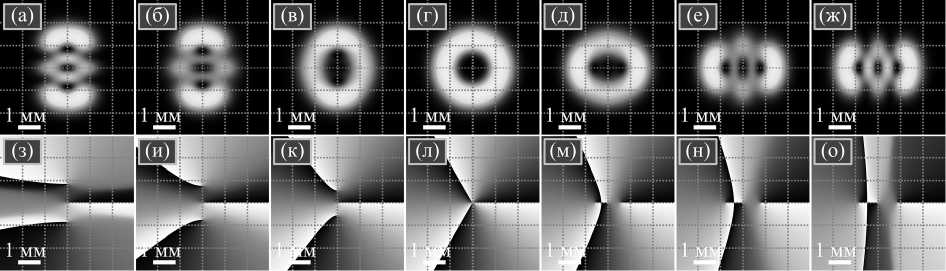
Рис. 5. Распределения интенсивности (а – ж) (чёрный цвет – ноль, белый цвет – максимум) и фазы (з – о) (чёрный цвет – 0, белый цвет – 2π) моды вАГ при (p, q) = (3, 3) для ε = –20 (а, з), –3 (б, и), –1 (в, к), 0 (г, л), 1 (д, м), 3 (е, н), 20 (ж, о)

Для полей с рис. 4 численно рассчитанные значения ОУМ составили 1,649836 (ε = –20), 1,331690 (ε =– 3), 1,081385 (ε =–1), 0,999992 (ε =0), 1,081385 (ε = 1) 1,331690 (ε =3), 1,649836 (ε = 20). Соответствующие теоретические значения, полученные по формуле (21), равны 1,649851 (ε =–20), 1,331704 (ε =–3), 1,081395 (ε =–1), 1,000000 (ε =0), 1,081395 (ε = 1), 1,331704 (ε =3), 1,649851 (ε =20).

Для полей с рис. 5 численно рассчитанные значения ОУМ составили 1,822821 (ε = –20), 2,396060 (ε =– 3), 2,900522 (ε =–1), 2,999974 (ε =0), 2,900522 (ε = 1), 2,396060 (ε =3), 1,822821 (ε = 20). Соответствующие теоретические значения, полученные по формуле (21), равны 1,822836 (ε =–20), 2,396077 (ε =–3), 2,900545 (ε =–1), 3,000000 (ε =0), 2,900545 (ε = 1), 2,396077 (ε =3), 1,822836 (ε =20).

Таким образом, теоретические значения ОУМ и рассчитанные численно совпадают до 3 знака.

Для рис. 3–5 был также рассчитан ТЗ. Для всех распределений на рис. 3 и 5 он составил соответственно 2 и 3. Для рис. 4 он составил 1 для ε =–3, –1, 0, 1, 3, и 3 для ε = ±20. Получается, что при разных значениях q < p (рис. 4) ТЗ не сохраняется, а увеличивается от q = 1 до p =3 при увеличении параметра ε от 0 до +20 или уменьшения его от 0 до –20. Этот эффект возникает из-за малой окружности вычисления ТЗ – непосредственно вблизи области существенной интенсивности. Если расширить вычислительную область на рис. 4о, то, аналогично рис. 4н, в дополнение к трём вихрям с ТЗ, равным +1, появятся два вихря с ТЗ, равным –1: один слева от расчётной области и один справа. В ре- зультате итоговый ТЗ всего поля, рассчитанный по формуле М.В. Берри вдоль окружности бесконечного радиуса, равен 1, хотя на распределении интенсивности на рис. 4ж отчётливо видны три нуля.

Заключение

В работе получены следующие результаты. Приведены явные выражения для комплексных амплитуд вихревых мод АГ, в зависимости от параметра эллиптичности ε для малых значений индекса p =2, 3, 4, 5 (уравнения (16) – (18)). Из них нетрудно получить выражения для вихревых мод АГ в предельных случаях при ε =0 и ε =±∞, согласующиеся с формулами (22) для общего случая. Для указанных вихревых мод АГ получены явные выражения для ОУМ в зависимости от параметра ε (уравнения (21) и в предельных случаях (уравнение (18)). В общем виде показано, что зависимость ОАМ от параметра ε является чётной функцией (уравнение (29)). Показано, что при ε =0 топологический заряд вихревых мод АГ равен топологическому заряду моды ЛГ, то есть второму номеру q , а при ε =+∞ равен первому номеру p . Численное моделирование это подтверждает при условии, что топологический заряд вычисляется по окружности, охватывающей область существенной интенсивности пучка. Тем самым, топологический заряд вихревых мод АГ не сохраняется при изменении параметра ε.

Работа выполнена при поддержке гранта Российского научного фонда № 23-12-00236 (в части теории) и в рамках Государственного задания НИЦ«Курчатовский институт» (в части моделирования).