"Винтовой" пространственный фазовый фильтр

Впервые "винтовые” фазовые фильтры были упомянуты в [ 1J, где было предложено выражение для функции пропускания пространственного фазового фильтра, фокусирующего в узкое кольцо. В [2] были описаны "винтовые" дислокации когерентного волнового поля. В местах таких дислокаций волновой фронт описывается комплексной амплитудой, фазовая часть которой тождественна фазовой функции пропускания "винтового” фильтра из [ I ]. В работе [3] "винтовой" фазовый фильтр применен для реализации оптического преобразования Ханкеля. Также в [3] впервые сообщается о реализации такого фильтра с помощью технологии компьютерной оптики. В [4] описано применение "винтового” фазового фильтра для задач оптической обработки информации: выполнения операции дифференцирования и оптического осуществления преобразования Гильберта для радиально-симметричных когерентных световых полей.

В данной работе приводятся новые аналитические выражения, связанные с дифракцией когерентного света на "винтовых” фазовых фильтрах.

"ВИНТОВОЙ" ФИЛЬТР ДЛЯ ФОКУСИРОВКИ в кольцо

Под ’’винтовым” фазовым фильтром здесь понимается пространственный фильтр с функцией комплексного пропускания F (р,у>) вида

f(p,^ - A(p)e^im*                                                                  0)

где m = 1,2,3,... , А (р) - амплитудно-фазовая функция, зависящая только от радиальной переменной, (р, р) - полярные координаты в плоскости фильтра.

В [1] предлагалось использовать для фокусировки в кольцо оптический фазовый элемент с функцией пропускания Ff (р.<р) вида

F1(p,^)= sgn [jm (ар)} е‘тЛ                                                                <2> где sgn [f(x)} - знакомая функция, Jm (х) - функция Бесседл первого рода т-го порядка. Оптическая схема для расположения фильтра (2) согласно [1] показана на рис. 1. Обозначения на рис. 1 следующие: X - длина волны света, а - радиус линзы и фильтра, которые расположены вплотную друг к другу, f - фокальное расстояние линзы, R - радиус кольцевого распределения интенсивности света в фокальной плоскости.

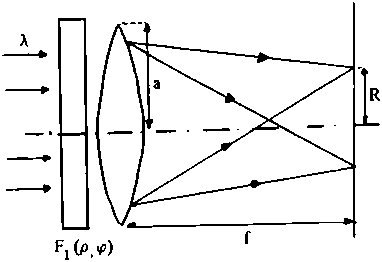
Рис. 1

Обоснование, что фильтр (2) формирует кольцо в фокальной плоскости линзы, в работе [1] дано с привлечением результатов численного моделирования. Понять же это можно следующим образом. Если бы пропускание фильтра Fj (p,ip) имело бы вид

F,(p,4>) = Jm ^ e'mV7.

то в фокальной плоскости световое поле, продифрагировавшее на таком фильтре, имело бы распределение амплитуды Ф (г, ф) в виде

” 2я -           jk ф (г.Ф)= / J F. (р,ф)ехр [—— г р cos (<р —*)] pdpd.p =

0 0                      *

= е™^ Лт(ар) Up rp)pdp= eimtS(a-A r),                                     (4)

где k - волновое число света, 6(x) -дельта-функция Дирака. То есть распределение интенсивности было бы в виде бесконечно узкого кольца с радиусом R = ~~ . Если в функции пропускания F] (р.р)заменить амплитудную часть на единицу, а оставить только фазовую часть, при этом получим функцию пропускания (2) вместо (3), то основная часть энергии излучения, из-за сохранения фазовой части функции пропускания, по-прежнему будет фокусироваться в кольцо с радиусом R = -^ ■ , а оставшаяся часть падающей на фильтр (2) энергии (около 20%) будет собираться в кольца с другими радиусами.

Оказывается можно сформировать световое поле перед линзой (рис. 1), описываемое комплексной амплитудой вида (3), с помощью фазового пространственного фильтра с пропусканием

F2(p,^)= е^"*’. а>0,                                                        (5)

причем данный фильтр будет уже всю энергию (за исключением дифракционных потерь) фокусировать в кольцо a f с радиусом R = —— .

Наличие ’’винтовой" составляющей в функции пропускания (5) обеспечивает отсутствие изолированного максимума энергии в нулевой пространственной частоте фокальной плоскости. Заметим, что радиально-линейная составляющая фазы в функции пропускания описывает пропускание аксикона, который уже применялся для фокусировки в кольцо [5].

Получим выражение, описывающее максимальное значение интенсивности света в кольце на радиусе R = = —— в зависимости от параметра о аксикона или от требуемого радиуса кольца R. Распределение комплексной амплитуды света Ф (г, ф) в фокальной плоскости линзы для пропускания фильтра (5) будет иметь вид к *к^ *эг г^ 00 2я -iop imp i7rpcos(tp-V)

Ф(г, ^)=~7~е е" f f е е е ^f          pdpdvp.                                        (6)

1                 о о

Максимальное значение модуля 1Ф (г, ф)( находится из условия равенства нулю фазы в подынтегральном выражении (6), то есть при условии к .

ар= —7— rpcos^-V'), к которое выполняется для точек кольца с радиусом а=— г или а Г

(?)

При этом условии вместо (6) получим выражение k ikf i-z7-R2a -iop

Ф(1М)= — е е е2 /е Jm (ар) pdp.                                          (8)

Пусть далее для простоты m - 1, тогда, воспользовавшись известным выражением (стр. 39 в [61)

Л,х Jj (x)xdx= ——[J, (t)-iJ2(t)L(9)

получим для максимальной интенсивности в Фурье-плоскости I(R) выражение к а4

l(R) = 1Ф (R, ^Р = (у)2 у Р2 («а) + Jj (аа)] ,(Ю)

f или в обозначениях: си -       ~ радиус дифракционного пятна, R - радиус требуемого кольца, получим следую щее выражение а о о R з R

• •W= W^ ²I^Ji^⁺4(y)l-                           (И)

Из (И) видно, что при стремлении R к нулю интенсивность на кольце стремится к нулю как R2, а при стремлении R к бесконечности интенсивность на кольце стремится к нулю как R-1.

Аналогичное выражение можно получить и при m = 0, то есть для случая, когда в качестве фильтра используется только аксикон без "винтовой” составляющей. При этом вместо (9) воспользуемся выражением (стр. 39 в ^

eixJ0(x)xdx= е^ [U^O-y М*)1+1Т М^Г(12)

0                         L               3                3

Тогда получим выражение для максимальной интенсивности на кольце, сформированном только аксиконом

*i(R) =     (~)21 J? (А) +Ji (“^ + 7" <~)2 I Ji (—)1 (—)"2 -

• ¹         IM Cd ¹ Cd ^z Cd 2Я Cd ¹ Cd Cd

  --i-eik'iit-^M'^i-с»)

Из сравнения (11) и (13) видно, что выражение для Ij (R) отличается от выражения для I(R) слагаемым (второе слагаемое в квадратных скобках в (13)), которое при стремлении R к нулю не зануляется, а стремится к постоянной —^— (-И-)2. Это подтверждает вывод о том, что наличие в оптическом элементе для фокусировки в кольцо "винтовой” фазовой составляющей обеспечивает отсутствие излучения в центре плоскости фокусировки.

Из сравнения (11) и (13) также видно, что при увеличении R второе слагаемое в квадратных скобках в (13) становится гораздо меньше первого слагаемого. То есть выражения для Ц (R) и I(R) становятся почти одинаковыми при R > w . Это означает, что при фокусировке в кольцо с радиусом много большим радиуса дифракционного пятна добавление "винтового” фильтра не приводит к заметным преимуществам по сравнению с использованием только одного аксикона.

ДИФРАКЦИЯ СВЕТА НА "ВИНТОВОМ" ФАЗОВОМ ФИЛЬТРЕ

Получим выражение для распределения интенсивности света в зоне дифракции Френеля для случая освещения плоской монохроматической волной фазового фильтра с функцией комплексного пропускания в виде Fj (р) = = ехр (lip). В этом случае комплексная амплитуда светового поля Ф (р, i// ;z) получается как результат преобразования Френеля-Бесселя от функции F3 (р):

ь ikz -4г7Р2°°2л «р -iKr2 i~rpcos(^-ip)

Ф (р,ф;г) = -^-е е / / е е 2z е z           rdrd

= -^ е12 е" ^е^ 7 е" ^J. Лгр)rdr.(14)

Z                       оZ

Далее используя выражение (стр. 198 в [6])

• 2яс

7х.^ ,1Mdx.^jz=-'T^vv^)tMos> получим вместо (14) следующее выражение

Ф (р,ф;г) = Д- J^pe^’^ [UQ (у~Р2) + J, (у-р2)],(16)

2 2z               и 4z * 4z где А (р, V/)=kz*mi//- Д-р2--- ■ 2z 4

Окончательное выражение для интенсивности света в зоне дифракции Френеля для случая падения плоской волны на "винтовой” фазовый фильтр имеет вид

• 1    W= у х² [J² (х²) + J² (х²)1 ,                                                                (17)

где х = р V -^-. Вид функции 1(х) показан на рис. 2. Из рисунка видно, что по мере распространения света в пространстве за фильтром в центральной части светового пучка образуется область с пониженной интенсивностью, которая расширяется пропорционально расстоянию z. Радиус этой области пониженной интенсивности равен х0 ^ 1 или Ро 31 2 V-|-. Так как интеграл в (14) берется в бесконечных пределах, то есть считается, что размеры фильтра де ограничены, то величина интенсивности 1(х) не спадает при стремлении р к бесконечности, а асимптотически стремится к постоянному значению (см. рис. 2).

1(Х)

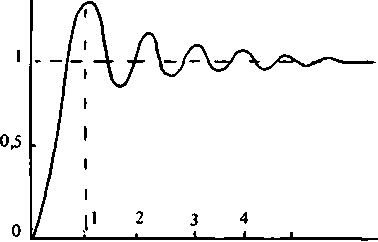
Рис. 2

Получим далее выражение для комплексной амплитуды света в дальней зоне для случая дифракции плоской монохроматической волны на "винтовом” фазовом фильтре с радиусом а. При этом вместо (14) выражение для амплитуды света Ф_[ (р, ф) будет иметь вид ь    ik z — «г—р im v а ь

Ф, (Р,^)= ~ е е “ е / Jj (~ур г) rd г.(18)

Для вычисления интеграла в (18) воспользуемся выражением (стр. 39 в [6])

/ J,(x)xdx = ~у U^ «)H0(i)_ J0«)H, «)],(19)

где Нп({) - функция Струве, которая имеет вид для п = 0,1:

Hq (х) = -у [х - -^- + J^ —...] = -у- i^F2 0: — ; —; — —),

• 11    --2_ г 5—__₊ —2L--1 ₌ 2х² р /]. _3_. _5_. —х—,

• Н1    я 1 3     9-5    9-25-7           я 12    2 ’ 2 ’4

где t F2 (а; b;с;х)— гипергеометрическая функция.

Для интенсивности света в дальней зоне дифракции с учетом (19) получим вместо (18) выражение

• 1, (Р)= 1Ф, (р. W2 = -f -^ (t-) но ф -Jo ^ Н1 ф!2-

• где ы = "~-   - радиус дифракционного пятна, z - расстояние от фильтра до плоскости наблюдения, а - радиус

фильтра. Из (20) следуют асимптотические оценки:

Ц (Р)~Р- Р -" 0

ЦбО-р ¹; Р^”.

Из (17) и (20) видно, что на всем протяжении распространения света, продифрагировавшего на "винтовом фазовом фильтре, в центральной части пучка нет энергии излучения.

ЗАКЛЮЧЕНИЕ

В работе предложено использовать для фокусировки в кольцо оптический элемент с функцией пропускания вида (5), в котором наряду с радиально-линейной составляющей фазы, описывающей пропускание аксикона, име- ется азимутально-линейная (’’винтовая”) составляющая фазы, которая обеспечивает отсутствие энергии света в центральной точке плоскости фокусировки.

Получены выражения (11) и (13) для зависимости максимальной интенсивности света на кольце от радиуса самого кольца.

Получены выражения (17) и (20) для распределения интенсивности света в зонах дифракции Френеля и Фраунгофера (дальняя зона) для случая дифракции плоской монохроматической волны на ’’винтовом” фазовом фильтре. Показано, что на всем протяжении светового пучка, продифрагировавшего на фильтре, энергия света в центре пучка равна нулю.