Виртуальное моделирование эксперимента при статических испытаниях силовых панелей конструкции планера летательного аппарата

создаваемого изделия. Это в полной мере касается вопросов проектирования и отработки прочности конструкции летательного аппарата (ЛА). Значительное внимание здесь уделяется экспериментальному подтверждению выбранных при проектировании критериев статической прочности конструкции. Это, как правило, выполняется на основе ис- пытаний конструктивно подобных образцов силовых агрегатов планера летательного аппарата. Однако возможности эксперимента при воспроизведении сложного, многокомпонентного нагружения того или иного силового элемента конструкции часто оказываются ограниченными, и испытания проводятся на простые виды нагружения. В этой ситуации виртуальное моделирование эксперимента приобретает особое значение. Оно позволяет прогнозировать поведение испытуемого образца при сложном нагружении, оценивать его работу в составе конструкции и анализировать корректность условий проведения эксперимента. Основой для этого служит валидация расчетной модели по результатам сопоставления расчетных и экспериментальных данных на простые случаи нагружения. В задачах прочности одним из основных методов виртуального моделирования является метод конечных элементов (МКЭ). Последние достижения в области этого метода дают возможность учитывать многие нелинейные факторы, возникающие в процессе нагружения конструкции, такие как нелинейность диаграмм σ‒ε, наличие больших перемещений, что является характерным для тонкостенных конструкций. В этом плане нелинейная версия МКЭ является хорошим инструментом расчетного сопровождения экспериментальных работ по оценке прочности, устойчивости и несущей способности элементов и агрегатов конструкции ЛА.

Одними из основных элементов силового каркаса планера ЛА являются подкрепленные панели. Характерная особенность данных элементов конструкции – их тонкостенность и связанные с ней вопросы местной устойчивости и закритического деформирования. При предельных нагрузках в стрингерных панелях в значительной мере могут проявляться различные нелинейные эффекты, связанные с возникновением местной потери устойчивости ее элементов и пластических деформаций. Последнее предопределяет необходимость использования нелинейных методов при расчетной оценке их несущей способности. Однако применение этих методов требует особых подходов, что проявляется как в области корректного построения конечно-элементной модели (КЭМ) панели, так и в особенностях анализа получаемых результатов [1; 2; 3].                33

В рамках данной работы приведены результаты по виртуальному моделированию статических испытаний на сжатие трехпролетных стрингерных панелей каркаса ЛА. Несущая способность многопролетной панели на сжатие, полученная в лабораторных условиях, достаточно хорошо характеризует ее несущую способность в конструкции ЛА при адекватных условиях нагружения. В этом случае наиболее полно реализуются условия реальной работы панели и учитываются взаимное влияние пролетов, жесткость соединенных с панелью шпангоутов, прочность крепежа, конструктивные особенности крепления полки стрингера к шпангоуту. Так, результаты натурных статических испытаний планера ЛА показывают, что критические напряжения общей потери устойчивости панелей хорошо совпадают с критическими напряжениями трехпролетных панелей, испытанных на сжатие при опирании крайних пролетов в торец [4].

Как правило, для испытаний используется панель длиной в три пролета между шпангоутами и по ширине в 4–6 стрингеров (рис. 1). С помощью двух стенок и четырёх шпангоутов две панели соединяются в кессон

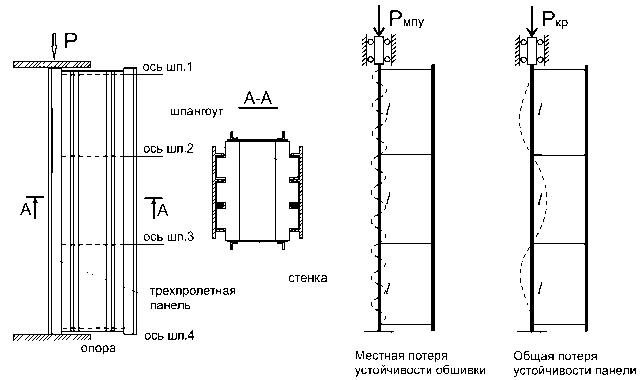
Рис. 1. Схема нагружения панелей, объединенных в кессон

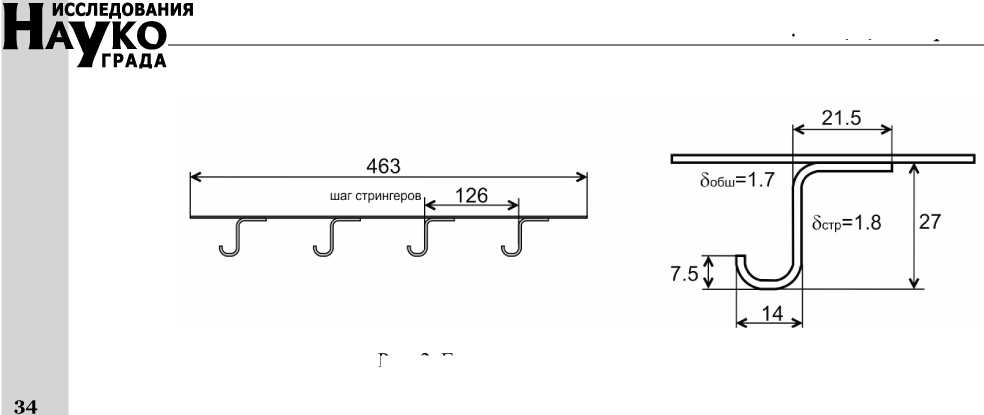
Рис. 2. Геометрические параметры панели, мм

для реализации в среднем пролете условий опирания, близких к реальным. Крепление поясов шпангоутов с панелью идентично натурной конструкции. Стенки устанавливают между панелями и дискретно соединяют со шпангоутами. Жесткость стенок должна быть выбрана таким образом, чтобы реализовы- валась потеря устойчивости панели между шпангоутами.

Испытания панелей кессона как замкнутой системы проводятся поочередно. Одна панель устанавливается по центру жесткости поперечного сечения между опорами испытательной машины, вторая панель свободна и служит вместе со шпангоутами и боковыми стенками устройством, препятствующим выходу из плоскости узлов пересечения панели со шпангоутами. Для контроля центровки панелей и фиксации критических напряжений местной и общей потери устойчивости между пролетами панели на обшивке и стрингерах устанавливают тензодатчики. Также в процессе нагружения панели производятся замеры сближения торцов и прогибов пролетов панели из плоскости.

На рис. 2 показаны основные геометрические параметры четырехстрингерной экспериментальной панели: толщина обшивки – 1,7 мм, толщина стрингеров – 1,8 мм, шаг стрингеров – 126 мм, шаг шпангоутов – 540 мм.

При изготовлении элементов кессонов применялись следующие материалы: обшивка, шпангоуты и боковые стенки – 1163РДТВ, стрингера - В95Т2. Всего было испытано четыре панели (два кессона). Нагружение панелей проводилось до исчерпания ими несущей способности и разрушения. В процессе деформирования панелей зафиксирована местная потеря устойчивости обшивки между стрингерами при значениях напряжения в панели омпу = 5,6 кгс/мм2 (среднее значение для четы- рех панелей). Дальнейшее нагружение приводит к разрушению панелей при среднем уровне действующих напряжений оопу = 11,4 кгс/мм2. Разрушение панелей происходит в результате общей потери устойчивости с образованием поперечной складки, направленной внутрь кессона в одном из крайних пролетов.

Центральный пролет в момент разрушения выпучивается наружу. Характерная форма местной потери устойчивости обшивки экспериментальной панели представлена на рис. 3, а , а характер разрушения панели – на рис. 3, б .

Рассмотренные экспериментальные исследования сопровождались соответствующими расчетами, которые проводились на основе нелинейной версии МКЭ, реализованной в комплексе программ NASTRAN/PATRAN [5]. Расчетная модель представляет собой трех-

а                       б

Рис. 3. Характерные формы местной потери устойчивости ( а ) и разрушения экспериментальных панелей ( б )

пролетный кессон, сформированный двумя четырехстрингерными панелями, боковыми стенками и имитаторами шпангоутов (рис. 4).

Подробность моделирования выбиралась таким образом, чтобы обеспечить достаточно надежное описание возможных местных форм потери устойчивости клеток обшивки и стрингеров. В частности, обшивка разбивалась на 8 конечных элементов (КЭ) на расстоянии между стрингерами, а стенка стрингера – на 2 КЭ. Моделирование велось на основе изгибно-мембранных конечных элементов типа QUAD4. Соединение обшивки и стрингеров панели выполнялось балочными элементами, моделирующими заклепки. На рис. 5 приведен фрагмент КЭМ трехпролетного кессона – четырехстрингерная панель с имитаторами шпангоутов.

Задача решалась в геометрически и физически нелинейной постановке. Учет геометрической нелинейности обеспечивался высокой степенью дискретности КЭМ, позволяющей достаточно надежно описывать местные формы потери устойчивости и их закритическое развитие. Учет физической нелинейности выполнялся на основе задания соответствующих диаграмм σ‒ε для материалов конструкции.

Граничные условия и нагружение кессона были аналогичны условиям эксперимента: один торец панели опирался, а другой торец нагружался в центре жесткости сечения равномерно распределенным усилием сжатия.

Применение нелинейной версии МКЭ к расчету устойчивости тонкостенных конструкций требует всестороннего и тщательного анализа получаемых результатов. Это связано, прежде всего, с тем обстоятельством, что решение подобных задач, как правило, завершается аварийно вблизи точек бифуркации (смены форм равновесия) в силу отрицательной определенности матрицы жесткости либо расходимости итерационного процесса. Однако вопрос о том, насколько мы приблизились к критической точке, часто остается открытым, поэтому при анализе результатов решения необходимо контролировать процесс прохождения решения задачи. При силовом нагружении панели это удобно выполнять на основе анализа графиков сближения торцов панели и прогибов стрингеров в зависимости от процента приложенной нагрузки. В качестве дополнительного средства контроля может служить уровень достигнутого напряжения в стрингерах, поскольку разрушение панели может произойти по причине исчерпания его прочности при нагрузке, меньшей нагрузки общей потери устойчивости.

В результате расчета были получены следующие результаты. При нагрузке Р_мпу = = 7 190 кгс происходит местная потеря устойчивости обшивки, средние критические напряжения при этом о_мпу = Р_мпу/F_пан = 5,9 кгс/мм² (где F_пан = 1 210 мм² - площадь сечения панели). При увеличении нагрузки происходит дальнейший рост прогибов обшивки. Сжимающему усилию Р опу = 14 310 кгс соответствует общая потеря устойчивости панели по трем полуволнам на пролетах, средние критические напряжения при этом о_опу= 11,8 кгс/мм². На рис. 6 и 7 показаны деформированные состояния КЭМ кессона при местной и общей потере устойчивости панелей.

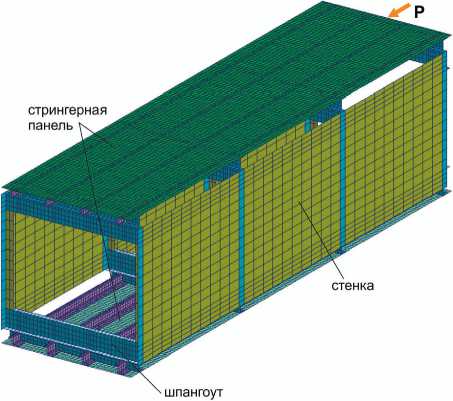
Рис. 4. КЭМ экспериментального трехпролетного кессона

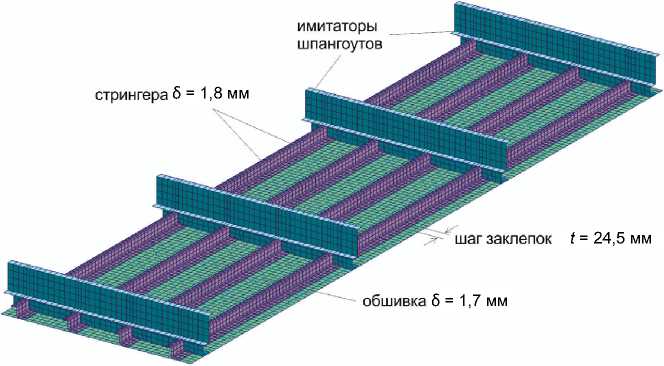
Рис. 5. Моделирование четырехстрингерной панели

U ИССЛЕДОВАНИЯ

Havko- жГРАДА

На рис. 8 показан график роста сближения торцов панели в зависимости от приложенного сжимающего усилия. При нагрузке 7 190 кгс наблюдается излом графика, что свидетельствует об изменении жесткости панели в результате местной потери устойчивости обшивки. При нагрузке 14 310 кгс происходит резкий рост продольных деформаций панели при незначительном увеличении нагрузки, т.е. можно говорить о том, что мы находимся вблизи критической точки общей потери устойчивости панели. Зависимость роста прогиба стрингера из плоскости (в среднем пролете) показана на рис. 9, здесь также в конце

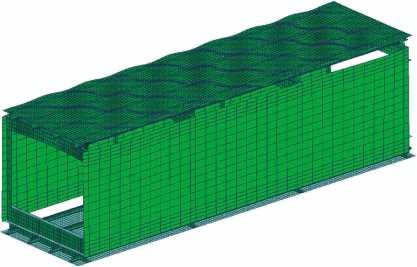
Рис. 6. Местная потеря устойчивости обшивки при сжатии панели

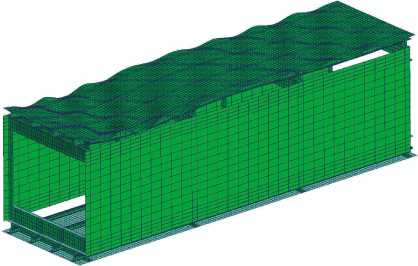
Рис. 7. Общая форма потери устойчивости панели

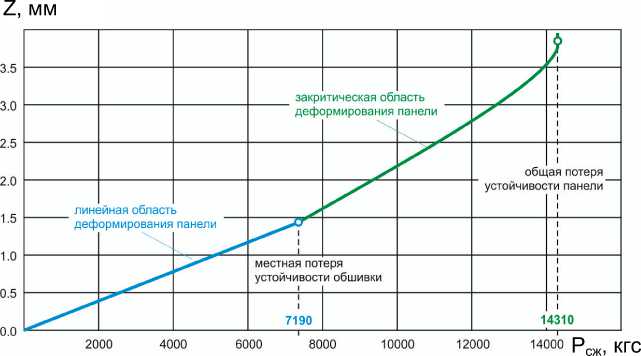
Рис. 8. Зависимость роста сближения торцов панели от приложенной нагрузки сжатия

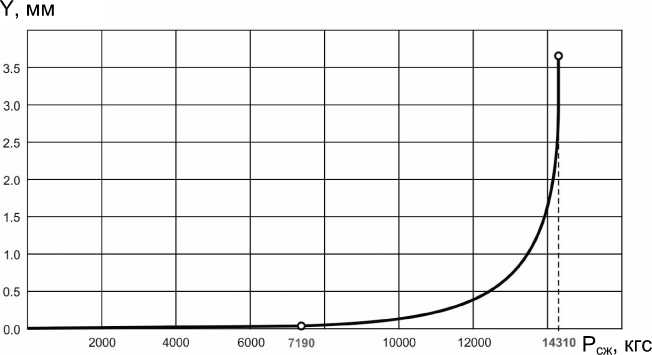
Рис. 9. Зависимость роста прогиба стрингера из плоскости от приложенной нагрузки сжатия

процесса прослеживается резкое нарастание прогиба стрингера с производной, стремящейся к бесконечности.

На рис. 10 приведено деформированное состояние трехпролетной панели при критической нагрузке общей потери устойчивости и распределение эквивалентных по Мизесу напряжений. Видно, что деформация конструкции характерна для общей формы потери устойчивости панели при сжатии, а уровень достигнутых напряжений в обшивке и стрингере достаточно высок и превышает предел текучести для материалов конструкции.

Таким образом, анализ откликов конструкции на прилагаемую нагрузку дает возможность утверждать, что разрушение панели произойдет при среднем уровне критических напряжений, равном 11,8 кгс/мм2.

В процессе эксперимента продольные деформации панели измерялись одиночными тензодатчиками, расположенными на обшивке и стрингерах в средних сечениях каждого из пролетов. Схема расположения тензодатчиков на панели приведена на рис. 11.

Сравнение расчетных и экспериментальных данных (рис. 12) представлено в среднем сечении панели в виде зависимости осреднен-ных по сечению напряжений от измеренных тензодатчиками деформаций.

Как видно из графиков, имеет место достаточно хорошее совпадение результатов как в качественном, так и в количественном отно- 37 шении. Расчетные и экспериментально замеренные деформации хорошо согласуются как на линейном, так и на закритическом участке деформирования панели. Так, разница между расчетными и экспериментальными данными по напряжениям местной и общей потери устойчивости - менее 5 %. Некоторое расхождение показаний тензометрии с расчетными

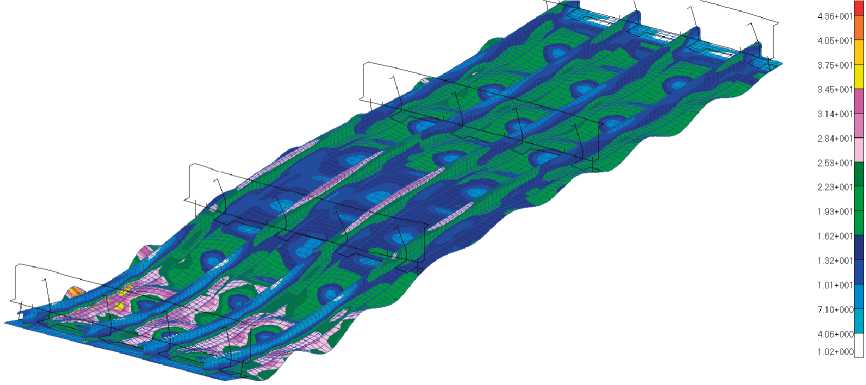
Рис. 10. Распределение эквивалентных по Мизесу напряжений при общей потере устойчивости панели

тензодатчики на обшивке

тензодатчики          тензодатчики на полке стрингера     на стенке стрингера

Рис. 11. Схема расположения тензодатчиков на обшивке и стрингерах панели

ИССЛЕДОВАНИЯ

AVKO-

Ж ГРАДА

стенка стрингера а, кгс/мм2

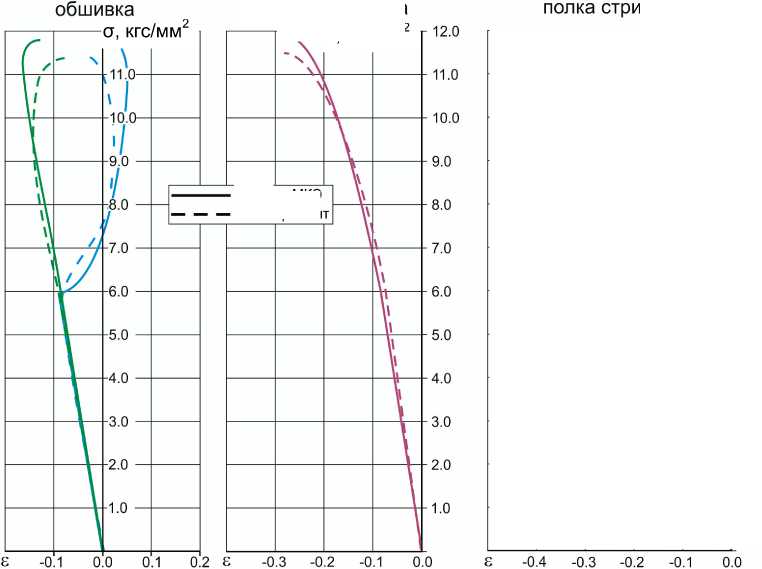
Рис. 12. Сравнение расчетных и экспериментальных деформаций

Расчет МКЭ

—			а, кгс	: /мм2	-    12.0 -    11.0 -    10.0 -9.0 -8.0 -7.0 -6.0 -5.0 -4.0 -3.0 -2.0 -1.0
	X X \
		\
		\
			\ \
			\\ \\ V
				А
				л

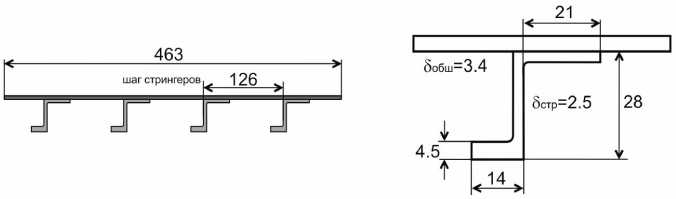
Рис. 13. Геометрические параметры панели, мм

Рис. 14. Вид разрушения панели

Виртуальное моделирование эксперимента при статических испытаниях

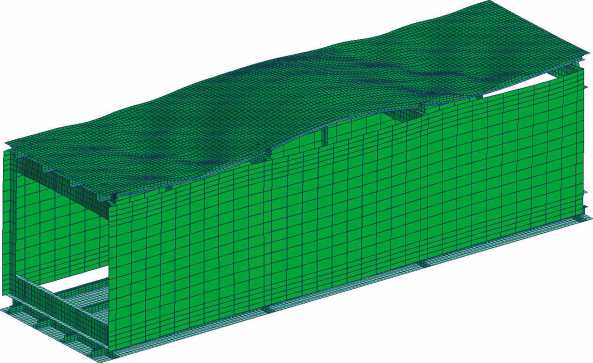
Рис. 15. Общая форма потери устойчивости панели данными в закритической области деформирования панели, очевидно, связано с тем, что расположение тензодатчиков не совпадает с узловой сеткой КЭМ, а также с достаточно условным моделированием сложной геометрии стрингеров.

Аналогичные результаты были получены при сравнении расчетных и экспериментальных данных для панелей, имеющих геометрические параметры, представленные на рис. 13.

Эксперимент показал, что разрушение панелей произошло по общей форме потери устойчивости в среднем пролете с выпучиванием его наружу и изгибом стрингеров при среднем уровне действующих напряжений °опу = 19,8 кгс/мм2. Разрушение сопровождалось разрывом стенок стрингеров и частично заклепочного соединения стрингера с обшивкой. На рис. 14 представлен характер разрушения панели.

Уровень разрушающих напряжений, полученный в расчете, равен о = 19,1 кгс/мм2. На рис. 15 показана общая форма потери устойчивости панели с выпучиванием в среднем пролете. Как видно, и для данной панели результаты расчета и эксперимента достаточно хорошо согласуются как в качественном, как и в количественном отношении.

Рассмотренные примеры показывают, что при корректном построении расчетной модели и соответствующем анализе результатов применение нелинейного МКЭ к оценке несущей способности элементов конструкции ЛА дает достаточно хорошее согласование расчетных и экспериментальных данных. В дальнейшем представленная конечно-элементная модель может использоваться для расчетной оценки несущей способности панели при различных комбинациях действующих на нее усилий.