Виртуальный пульт для управления вычислительным экспериментом в рамках молекулярной динамики

Потребность в современной технике двигает вперед разработку наноматериалов, свойства, которых моделируются с помощью методов молекулярной динамики. Такое моделирование проводится на суперкомпьютерах или компьютерных кластерах и называется вычислительным экспериментом. После проведения серии «виртуальных» экспериментов становится ясно наиболее перспективные варианты наноструктуры, которые соответствуют желаемым свойствам проектируемого материала. Управление такими экспериментами происходит обычно через скрипты или командную строку, и не позволяет управлять данным процессом. После запуска расчета полученные данные сохраняются в хранилище и требуют дальнейшей обработки, анализа и визуализации. Процесс обработки полученных данных занимает время, а хотелось бы иметь возможность влиять на эксперимент в ходе его проведения и видеть визуализацию моделирования в режиме «онлайн» (например, при увеличении температуры сразу увидеть, как это отразилось на моделируемом объекте). Цель данной работы показать, что процессом вычислительного эксперимента основанного на методах молекулярной динамики можно управлять.

Молекулярная динамика

Молекулярной динамикой называют методы компьютерного моделирования для изучения физических перемещений атомов и молекул моделируемого тела, которые во время вычислительного эксперимента взаимодействуют между собой в течение фиксированного периода времени, тем самым давая представление о динамической эволюции системы. Методы МД позволяют проводить моделирование системы при заданной температуре, с заданными скоростями моделируемых частиц, отслеживать состояние системы на каждом шаге, при этом вычисления проходят с достаточно высокой скоростью. Координаты частиц в каждый последующий момент времени вычисляются посредством интегрирования уравнений движения, в которые входят потенциалы взаимодействия частиц между собой и внешней средой [1].

Популярность моделирования материалов такими методами приобрела популярность благодаря возможности сохранять сотни параметров на каждом шаге компьютерного эксперимента, что не всегда возможно сделать в условиях натурного. Молекулярная динамика применяется к системам до 109 частиц, и дает глубокое понимание того, как различные системы подчиняются классическим законам физики [6]. Так как частиц при таком моделирование огромное количество, во время моделирования траектории не сохраняются, заботиться о траектории каждой отдельной частицы не нужно, чтобы не заполнить память устройства, на котором проводятся вычисления [4].

Виртуальный пульт

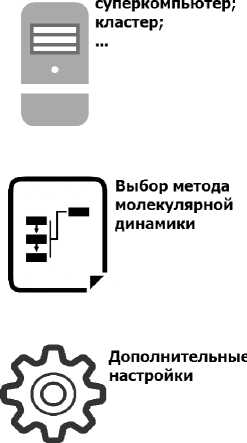
Вычислительные эксперименты проводят на суперкомпьютерах или компьютерных кластерах, управление данным процессом происходит через скрипты. После их запуска на электронную почту поступает сообщение о старте процесса. Если эксперимент завершается некорректно, то поступает сообщение с описанием ошибки остановившей исполнение процесса. После успешного завершения вычислительного эксперимента, данные содержатся в хранилище, и их можно обрабатывать, анализировать и визуализировать. Возникла идея упрощения процесса подготовки эксперимента с помощью виртуального пульта (см. рис. 1).

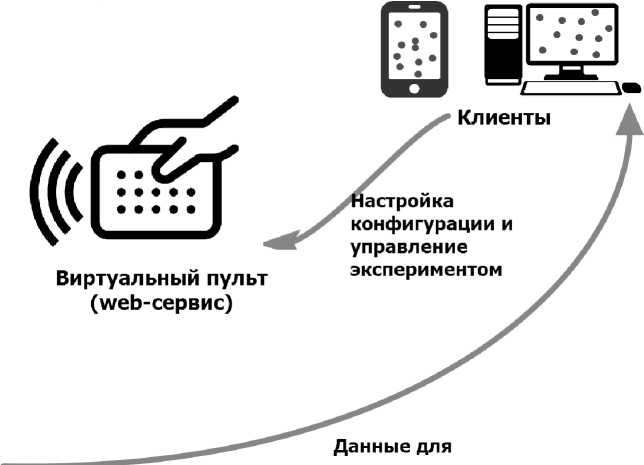
Виртуальный пульт должен помогать сконструировать вычислительный эксперимент из доступного набора аппаратных платформ, методов молекулярной динамики, модулей, хранилищ данных и т.д. А так же быть расширяемым и позволять подключать к нему новые аппаратные и программные модули. ВП это конструктор, который позволит при каждом новом вычислительном эксперименте выбрать желаемую конфигурацию, добавить отсутствующие методы или модули и существенно ускорить процесс подготовки эксперимента. Полученные в режиме реального времени данные с вычислительного эксперимента будут возвращаться клиенту, в котором открыт виртуальный пульт и представляться в удобном для человека виде, то есть предполагается визуализация в режиме «онлайн». В качестве клиента выступит персональный компьютер, который через интернет обменивается командами и данными с ВП. Возможно так же создание клиентского приложения для планшетов и смартфонов с большими дисплеями, что даст еще и мобильность данному пульту, ведь можно будет контролировать процесс, например в дороге на работу. Но создание мобильных приложений для данной задачи имеет ряд сложностей, например, низкая пропускная способность мобильных сетей в некоторых местах и связанный с этим процесс обработки данных для визуализации, которые должны быть, как можно больше сжаты.

Аппаратна платформа

Вычислительный эксперимент

визуализации (Координаты, скорость и т.д)

Рис. 1. Концептуальная схема мобильного виртуального пульта

Предполагается, что процесс использования виртуальным пультом будет прост, нужно будет зайти на сайт, пройти аутентификацию в своей учетной записи и начать настройку конфигурации нового эксперимента, либо запустить одну из сохраненных.

Прототип

Для демонстрации возможности управления вычислительным экспериментом было принято решение создать прототип. В качестве модели системы, которую будем моделировать, была выбрана «простая жидкость». Простыми жидкостями называют жидкие простые вещества, где нет химически связанных друг с другом атомов, образующих молекулы различной формы и размера [2]. То есть это абстрактная теоретическая модель, позволяющая упростить расчеты и проводить моделирование описанной системы в рамках классической молекулярной динамики. Молекулы в данной модели будут рассматриваться как упруго взаимодействующие шары конечного радиуса, а внутримолекулярная структура не учитывается при их взаимодействии.

В основе методов классической молекулярной динамики лежит модельное представление о многочастичной системе, в которой все частицы (атомы или молекулы) представляют собой материальные точки. Поведение отдельной частицы описывается классическими уравнениями движения Ньютона [1], которые задают закон эволюции динамической системы в пространстве и времени. Данные урав- нения включают полный набор переменных, определяющих состояние системы в конкретный промежуток времени (координаты, скорости и ускорения частиц), а так же их производные во времени, что позволяет, зная их состояние в конкретный период времени вычислить состояние системы. Уравнения могут быть записаны в следующем виде:

й2П    "с

^!m.,    ^f

Здесь i - номер частицы (1 < i <  N), N - количество частиц, m ; — масса конкретной частицы f -равнодействующая всех сил, действующих на частицу, имеющая следующее представление:

7 _ ди(Г_ь .. Л) ^{ft -}        dr_t

—»ex

+ ft ,

—►ex где U - потенциал взаимодействия между частицами, ft  - сила, обусловленная внешними полями.

Так как в качестве модели выбрана простая жидкость, и внутримолекулярная структура не учитывается, то мы предполагаем, что сила взаимодействия любых двух молекул зависит только от расстояния между ними. Значит, полная потенциальная энергия U определяется суммой двух частичных взаимодействий:

^{U -V(r} 12 ^{) +} И(Г 1з ) + ..+ У(Г 2з ) + .. - T, i_<j₌i V(r_i j ) , где V(r ;j ) - потенциал парного взаимодействия, который зависит от расстояния r^- между частицами i и j. Соответствует простым жидкостям, о которых говорилось выше.

В качестве среды, в которой будут находиться моделируемые частицы, подойдет тороидальная емкость (смотри рис. 2) . Данное допущение позволит не учитывать взаимодействие со стенками емкости, поскольку частица, выходя за пределы одной из граней будет входить в емкость через противоположную.

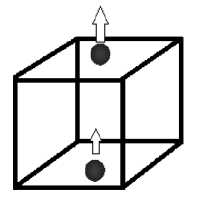
Рис. 2. Тороидальная емкость. Выходя за одну грань, частица попадает внутрь через противоположную

Реализация

Был создан прототип виртуального пульта, демонстрирующий возможность управления процессом вычислительного эксперимента в рамках двумерной молекулярной динамики. Создан web- сайт, в котором серверная часть написана на php, а клиентская на javascript. Поскольку прототип не имеет базы данных и не предполагает моделирование систем с количеством частиц более 255, то вычисления проводятся прямо на клиенте. А сервер отвечает за загрузку шаблонизатора Smarty и js- файлов. Для ускорения разработки графического интерфейса прототипа были использованы библиотека jQery, фреймворк Bootstrap 3 и т.д. Для удобства тестирования на виртуальной машине под управлением Ubuntu, созданной в Oracle VM VirtualBox был настроен виртуальный хост.

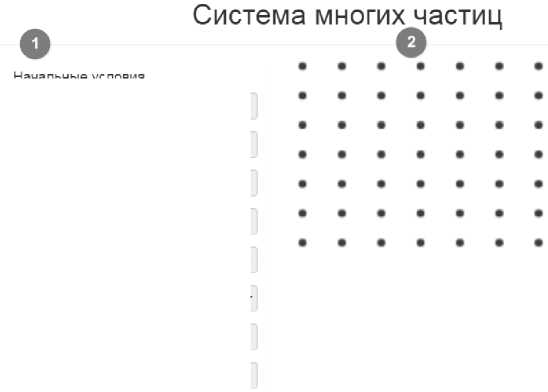
Графическая часть прототипа включает в себя блоки : начальных условий, визуализации и блок управления. В блоке начальных условий происходит выбор значений для старта вычислительного эксперимента. Поскольку частицы расставляются на квадратной сетке и их количество Nx и Ny равны, общее количество частиц будет равно п². Так же есть возможность настройки размеров блока визуализации, начальной кинетической энергии и шага dt. Начальное расположение частиц возможно тремя методами : прямоугольник, треугольник и случайным образом. В блоке визуализации можно видеть состояние системы на i —ой итерации вычислительного эксперимента.

Управление экспериментом происходит с помощью ползунков и кнопок снизу. Например, в ходе эксперимента можно увеличить температуру с помощью ползунка и увидеть в блоке визуализации как это отразилось на системе. Эксперимент можно проводить как пошагово, так и непрерывно. Так же есть возможность добавить в систему хаоса и выстрелить из левого нижнего угла частицей по системе частиц и посмотреть к чему это приведет.

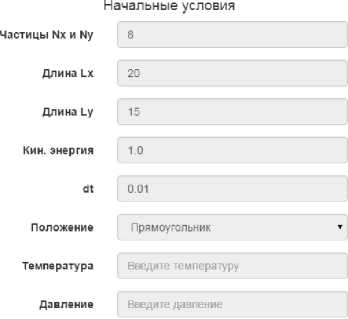
Температура

Давление

Рис. 3. Графический интерфейс прототипа виртуального пульта: 1 – блок начальных условий; 2 – блок визуализации; 3 – блок управления

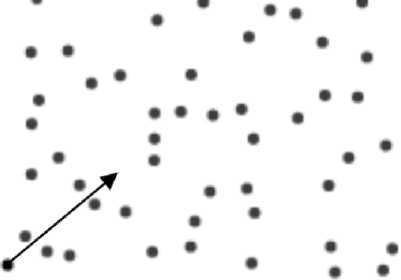
Рис. 4. Выстрел частицей

Рис. 5. Методы начальной сетки: 1 – прямоугольник; 2 – треугольник; 3 – случайным образом

Заключение

На примере созданного прототипа было показано, что возможно управлять вычислительным экспериментом в режиме реального времени. Дальнейшее развитие предполагает интегрирование всех частей вычислительного эксперимента в прототип виртуального пульта. Для этого понадобится суперкомпьютер или компьютерный кластер, хранилище для данных, а также специализированное программное обеспечение для разработки и построения вычислительных модулей для параллельных вычислений на GPU на базе технологии CUDA [3]. Разработка и внедрение виртуального пульта для интерактивного управления вычислительным экспериментом не только позволит значительно повысить эффективность теоретических исследований возможности создания новых наноматериалов, но и предоставит новые возможности для планирования натурных нанотехнологических экспериментов.