Визуализация 1-солитона пространственно-двумерного эволюционного уравнения А6
Автор: Алексеева Александра Валерьевна, Амирханова Гульшат Аманжоловна
Журнал: Проблемы информатики @problem-info
Рубрика: Теоретическая информатика
Статья в выпуске: 2 (27), 2015 года.
Бесплатный доступ
В работе представлены пространственно-двумерное эволюционное уравнение А6, иерархия его вспомогательных линейных систем, закон сохранения, его пространственно-двумерная билинейная форма Н2, его N-солитонные решения, визуализация 1-солитонного решения данного уравнения, исследование свойств и качеств 1-солитона, обработка данных, статистические таблицы.
Уравнение кортевега-де фриза, пространственно-двумерное эволюци¬онное уравнение, пространственно-двумерная билинейная форма, вспомогательная линейная система, закон сохранения
Короткий адрес: https://sciup.org/14320277
IDR: 14320277 | УДК: 517.957
Текст научной статьи Визуализация 1-солитона пространственно-двумерного эволюционного уравнения А6
Многомерные нелинейные уравнения, обобщающие классическое уравнение Кортевега-де Фриза, являются объектом интенсивных исследований в последнее время [1-7]. Интерес вызван тем, что уравнение Кортевега-де Фриза, как и его многомерные аналоги, является универсальной математической моделью, так как описывает многие нелинейные процессы в океанах, кристаллических телах, магнитных материалах, эфире, атмосфере Земли и других планет, живых организмах, экономике и др.
В 1949 году Ферми, Паста и Улама изучали нелинейные системы, которые позже были названы солитонами. Солитоны запоминали информацию и хранили ее очень долго, как молекула ДНК. Ученые утверждали, что солитоны ведут себя как разумные существа, но объяснить этот феномен не смогли.
В океанологии большое внимание уделяют изучению солитонов в морях и океанах, динамику которых описывает (2+1)-мерное эволюционное уравнение Аб. Их называют волны-убийцы, аномальные волны, волны-монстры, блуждающие волны. Они достигают высоты более чем 25-30 метров и представляют большую опасность для судов и морских сооружений. Появление волн-убийц не связано с катастрофическими геофизическими событиями. Они появляются неожиданно и также неожиданно исчезают. Ученые предпо- лагают, что явление волн-убийц связано с особенностями динамики солитонов и не зависит от внешних факторов. Динамику солитонов в морских и океанских водах описывают пространственно-двумерные обобщения уравнения Кортевега-де Фриза [8].
Ранее Алексеевой А. В. были выведены новые пространственно-двумерные нелинейные уравнения А1-А14 и AI-AXII [1], которые являются обобщениями классического уравнения Кортевега-де Фриза.
В данной работе представлены (2+1)-мерное эволюционное уравнение Аб, иерархия его вспомогательных линейных систем, закон сохранения, его (2+1)-мерная билинейная форма Н2, его N-солитонные решения, визуализация 1-солитонного решения данного уравнения, исследование свойств и качеств 1-солитона, обработка данных, статистические таблицы.
Рассмотрим (2+1)-мерное эволюционное уравнение Аб [1]:
Фt + ^xxy + 3 [ФУ]x = 0, гДе Vx = Фу, Ф = Ф (x, y, t) — достаточно гладкая комплекснозначная функция.
Интегрируемость (2+1)-мерного эволюционного уравнения Аб доказывает наличие высших иерархий его вспомогательных линейных систем уравнений:
у х = U o y + Ху,
У t = Ху у + Ау + ХВу,
Ух = Uoy + Ху, yt = Хуу + Ау + ХВу + Х2Су, ух = иоу + Ху, yt = Хуу + Ау + ХВу + Х2Су + Х3Dy, где Х = Х (y,t), Хt = ХХу, Vx = Фу.
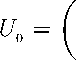
Ф
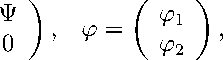
_ 0 __ -Фху - 3ФР
-Фху - 3ФV0
i_ _ -2iд-1Ф - V '
-2id-1^ - V -i,
| _ _ / i -2iд-1Ф \
' = ... = 2idx^
Ф = Ф (x, y, t), yi = yi (x, y, t), i = 1, 2 — достаточно гладкие комплекснозначные функции.
Закон сохранения для (2+1)-мерного эволюционного уравнения Аб имеет вид
∂T
——+ divF = 0, ∂t где T — плотность. F = (F1, F2) — поток.
divF = + dF2,
∂x ∂y
T = Ф + C 1 , F i = 3W + C2, f 2 = Фхх + Сз, Vx = Фу,
Ф = Ф (x, y, t) — достаточно гладкая котшлексиозиачиая функция. Cj. j = 2,3 — постоянные.
(2+1)-мерное эволюционное уравнение Аб можно привести к (2+1)-мерной билинейной форме Н2:
DxDt + DXDy) (у о у) = 0, где
D x D t (у о у) = 2 (^ xt y - ^x^t),
DXDy (у о У) = 2 (Ухххуу - TxxxTy - Зуxxyух + Зуххуху) , у = у (x, y, t) — достаточно гладкая комплекснозначная функция.
(2+1)-мерная билинейная форма Н2 является многомерным обобщением классической билинейной формы Хироты Н [8]:
(DxDt + DX) (f о f ) = 0, где
DmDn (F о G) = (dx - d x o) m (d t - d t o )n F (x,t) G0 (x0/)^=x,to = , f = f (x, t) — достаточно гладкая действительная функция.
Используя метод Хироты, находим солитонные решения (2+1)-мерного эволюционного уравнения Аб.
1-солитонное решение (2+1)-мерного эволюционного уравнения:
ф = 2(ln у^ , где yi = 1 + exp {ax + ву - ваЧ + y} ,
Ф = Ф (x, у, t). у 1 = у 1 (x, у, t) — достаточно гладкие комплекспозпачпые функции. а. в- Y — постоянные.
2-солитонное решение (2+1)-мерного эволюционного уравнения Аб:
Ф = 2(ln y2)xx , где
У2 = 1 + exp {ni} + exp {П2} + exp {ni + П2 + A12} , nj = ajx + ejУ - ejajt + Yj, j = 1,2, a2 - ai -в1а2 + в2а2 + (в1 - в2) (ai -а2 + ai -eia2 - в2a2 + (ei + в2) (ai + a2)2
—тд, ai = a2,
exp {Ai2}
Ф = Ф (x, y, t). у2 = y2 (x, y, t) — достаточно гладкие котшлексиозиачпые (фчпгтшп. aj. ej, Yji j = 1,2 — постоянные.
N-солитонное решение (2+1)-мерного эволюционного уравнения Аб:
Ф = 2(1n Vn )xx , где ^* „пробегает" все мне)жества. pj = 0, 1. j = 1, N.
NN
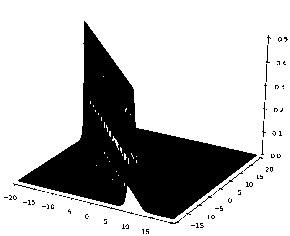
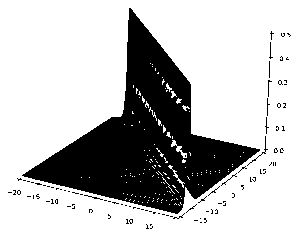
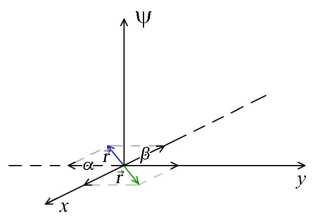
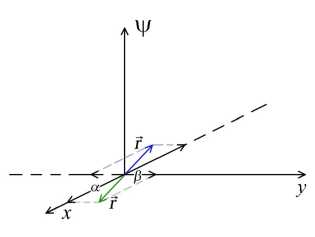
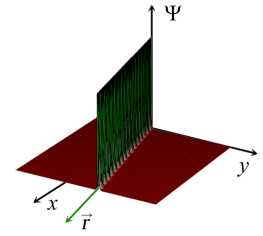
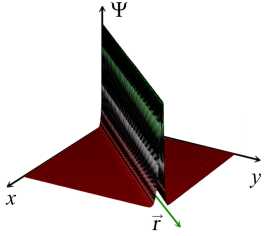
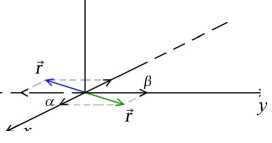
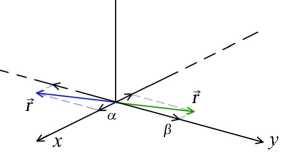
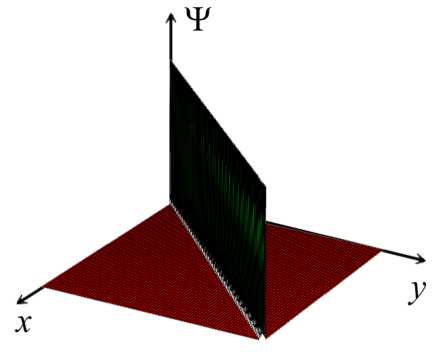
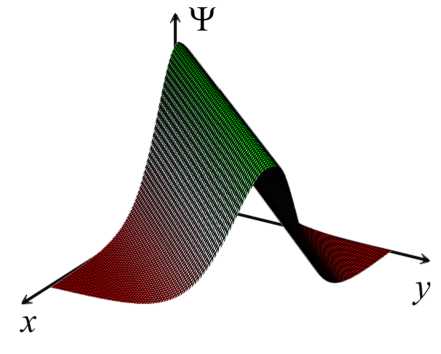
E Mini + E µi µj Aij , i=1 1≤i • —вia2 + вjaj + (вi — вj) (ai — aj) —вia‘i— вjaj + (в + вj) (ai + aj) ai = aj, i = j,i,j = 1,N, Ф = Ф (x,y,t).^N = ^N (x, y, t) — достаточно гладкие комплекспозпачпые функции. aj. вj• Yj, j = 1, N — постоянные. Запишем 1-солитонное решение (2+1)-мерного эволюционного уравнения Аб: ^ = 2 (In^)xx , ^ = 1 + exp {ax + ву — вa2t + y} в виде — ϕxxϕ ^2 ϕ2x , где Откуда имеем у2 = a2 exp {2ax + 2ву — 2ea2t + 2y } , VxxV = a2 exp {2ax + 2ву — 2ea2t + 2y} . 2 exp {2ax + 2ву — 2вa2t + 2y} Ф = 2a -----------------------------------5 (1 + exp {2ax + 2ву — 2вa2t + 2y}) или Ф = α2 2 ch2fax + ву — вa2t + y} Скорость 1-солитона (2+1)-мерного эволюционного уравнения Аб имеет вид v = α2βα — , а его амплитуда вычисляется по формуле A = —. Видно, что скорость 1- V a2 + в2 ' * солитона (2+1)-мерного эволюционного уравнения Аб и его амплитуда пропорциональны 2вА \' v = —, , т. е. чем выше волна, тем быстрее она бежит. V a2 + в2 Приведем компьютерную реализацию, анализ свойств и качеств 1-солитонного решения (2+1)-мерного эволюционного уравнения Аб. 1-солитонное решение (2+1)-мерного эволюционного уравнения Аб при a = 1, в = 1 Y = 0. t = 0 изображено на. рис. 1. На рис. 2-4 изображено 1-солитонное решение (2+1)-мерного эволюционного уравнения Аб в течение времени, изменяющегося от —10 до 10 пр и a = 1, в = 1 Y = 0. На рис. 5-12 показано, что постоянные a и в задают направление ~ = ai + в~, вдоль которого расположен 1-солитон (2+1)-мерного эволюционного уравнения Аб. Далее будем называть вектор ~ вектором направления солитона. Рис. 1. 1-солитон (2+1)-мерного эволюционного Рис. 2. 1-солитон (2+1)-мерного эволюционного уравнения Аб при а = 1, в = 1, Y = 0, t = 0 Рис.З. 1-солитон (2+1)-мерного эволюционного уравнения Аб при а = 1, в = 1, Y = 0, t = 5 ~ ~ Рис. 5. Направление ~ = а i + в j расположения 1-солитона (2+1)-мерного эволюционного уравнения Аб при а = 1, в = 1 (или а = — 1, в = —1), Y = 0, t = 0 ~ ~ Рис. 7. Направление ~ = а i + в j расположения 1-солитона (2+1)-мерного эволюционного уравнения Аб при а = 5, в = 1 (илиа = —5, в = —1) ,7 = 0, t = 0 уравнения Аб при а = 1, в = 1 Y = 0, t = —10 Рис. 8. Расположение 1-солитона (2+1)-мерного эволюционного уравнения Аб при а = 5, в = 1 (или а = —5, в = — 1)Л = 0, t = 0 Рис. 4. 1-солитон (2+1)-мерного эволюционного уравнения Аб при а = 1, в = 1 Y = 0, t = 10 Рис. 6. Расположение 1-солитона (2+1)-мерного эволюционного уравнения Аб при а = 1, в = 1 (или а = — 1, в = — 1) Y = 0, t = 0 Г / Рис. 9. Направление ~ = a i + в~ расположения 1-солитона (2+1)-мерного эволюционного уравнения Аб при a = 1, в = 5 (или a = —1, в = —5), y = 0, t = 0 Рис. 11. Направление r = a i + в j расположения 1-солитона (2+1)-мерного эволюционного уравнения Аб при a = 1, в = -5 (или a = — 1, в = 5), y = 0, t = 0 ■ Ндш.1_________________________________________1^^ 3=1 _________" - V X Щ^9ДЦЩЯ|___________»ЯЯ_у^1Ж1_^<™ы Рис. 13. 1-солитон (2+1)-мерного эволюционного уравнения Аб при a = 0, 1, в = 0, 5, y = 0, t = 0, основной вид Qngu„l щ^^-j ill 1 ИМ ЩО|©Д[ДВ|Я|___.=CM2S»3 Рис. 15. 1-солитон (2+1)-мерного эволюционного уравнения Аб при a = 0, 1, в = 0, 5, y = 0, t = 0, вид слева 'ill 111 Рис. 10. Расположение 1-солитона (2+1)-мерного эволюционного уравнения Аб при a = 1, в = 5 (или a = —1, в = -5), y = 0, t = 0 llllllliii Рис. 12. Расположение 1-солитона (2+1)-мерного эволюционного уравнения Аб при a = 1, в = -5 (или a = —1, в = 5), y = 0, t = 0 *й|О|© 4*1 ИВ|Н| >азым ,у=1221Я . =0Я®а11Я Рис. 14. 1-солитон (2+1)-мерного эволюционного уравнения Аб при a = 0, 1, в = 0, 5, y = 0, t = 0, вид сверху IWnr W|lll|ll|l|l|i|11 I^IOlO 4*1 ■'1в|я1____________________В-0Я21К1 ,р-1ЫВ .сСДШТС Рис. 16. 1-солитон (2+1)-мерного эволюционного уравнения Аб при a = 0, 1, в = 0, 5, y = 0, t = 0, вид справа Рис. 17. 1-солитон (2+1)-мерного эволюционного уравнения Аб при а = в = 5, Y = 0, t = 0 Рис. 18. 1-солитон (2+1)-мерного эволюционного уравнения Аб при а = в = 0, 1 Y = 0, t = 0 Таблица Сводная таблица параметров и характеристик 1-солитонов (2+1)-мерного эволюционного уравнения Аб различной амплитуды (а, в — постоянные, A — амплитуда, v — скорость) α β A, м v, м/с 1 1 0,5 0,7 4,5 β 10 20β p20,25 + β2 5 5 12,5 17,6 7,7 β 30 60β p59,29 + β2 10 10 50 70,7 Интересно отметить, что гладкий, ровный гребень 1-солитона (2+1)-мерного эволюционного уравнения Аб достигается только тогда, когда а = в, как показано на рис. 14, 6 и далее 17, 18. В случае неравных параметров а = в наблюдается эффект закручивания 1-солитона против часовой стрелки от вектора направления г, при этом гребень 1-солитона становится неоднородным и возникает эффект „морской пены“ на гребне волны, как по казано на рис. 8, 10, 12 16. а2 / х Амплитуда A = — 1-солитона (2+1)-мерного эволюционного уравнения Аб всегда ложительна. Следовательно, 1-солитон (2+1)-мерного эволюционного уравнения Аб по мо жет принимать только форму горы или холма, он не может быть впадиной, чего нельзя сказать о солитонах других пространственно-двумерных нелинейных уравнений Al-А14 и AI АХИ [1]. Направление движения 1-солитона (2+1)-мерного эволюционного уравнения Аб показывает вектор П, ортогональный вектору направления г, т. е. n±r. Далее будем называть вектор n вектором движения солитона. Из табл, видно, что 1-солитоны (2+1)-мерного эволюционного уравнения Аб могут иметь одинаковую амплитуду при разных скоростях. Например, в табл, показано, что скорости волн высотой в 10 и 30 метров, зависят от параметра в- Следовательно, скорость 1-солитона (2+1)-мерного эволюционного уравнения Аб зависит от вектора направления r = a i + в j илп вектор;-1 движения п. ортогонального вектору r. Таким образом, мы представили (2+1)-мерное эволюционное уравнение Аб, получили иерархию его вспомогательных линейных систем, вывели закон сохранения, показали его (2+1)-мерную билинейную форму Н2, нашли его N-солитонные решения, сделали компьютерную реализацию 1-солитонного решения (2+1)-мерного эволюционного уравнения Аб, исследовали свойства и качества 1-солитона данного уравнения, для наглядности собрали в таблицу некоторые данные и характеристики 1-солитона (2+1)-мерного эволюционного уравнения Аб.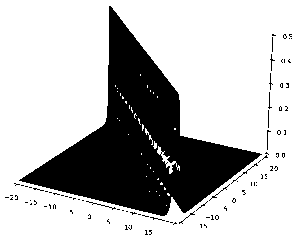




Список литературы Визуализация 1-солитона пространственно-двумерного эволюционного уравнения А6
- Alexeveva A.V. (2+l)-dimensional analogs of the Korteweg-de Vries equation//International Journal of Contemporary Mathematics. 2012. V. 3. N 1-2. P. 47-55.
- Алексеева А. В. (2+1)-мерное солитонное уравнение А9 и его решения/Современные проблемы гуманитарных и естественных наук: матер. XIV Междунар. науч.-практ. конф. Москва, 26-27 марта 2013 г. С. 13-18.
- Алексеева А. В. (2+1)-мерное нелинейное уравнение А10 и его солитонные решения/Тенденции и перспективы развития современного научного знания: Матер. VI Междунар. науч.-практ. конф. Москва, 29 марта 2013 г. С. 21-27.
- Alexeveva А. V. Solution of the (2+l)-dimensional soliton equation A3 by the Hirota's method/Applied Sciences in Europe: tendencies of contemporary development. Proc. of the 6th Internat. scien. conf. Stuttgart, Oct. 18, 2014. Stuttgart: ORTPublishing, 2014. P. 3-7.
- Alexeveva A.V. The (2+l)-dimensional soliton equation A7 and its bilinear form/Applied Sciences and technologies in the United States and Europe: common challenges and scientific findings.
- Alexeveva A. V. The (2+l)-dimensional soliton equation All and its bilinear form/Innovations in Technical and Natural Sciences. Proc. of the 3rd European conf. Vienna: „East West" Association for Advanced Studies and Higher Education GmbH, 2014. P. 63-68.
- Алексеева А. В. (2+1)-мерная модель Кортевега-де Фриза и ее интегрируемость//Вестник МОН РК. 2006. № 3. С. 12-15.
- Абловиц М., Сигур X. Солитоны и метод обратной задачи. М. 1987.


