Визуализация процессов работы аэропорта на основе системы массового обслуживания и компьютеризации управления полетами

нимается решение об изменение курса и скорости (с учетом возможных изменений). При передвижении учитывается необходимость соблюдения определенной дистанции между воздушными судами. Следовательно, воздушное судно должно изменять свою скорость и траекторию полёта так, чтобы не нарушить интервал движения. Имея информацию обо всех воздушных судах, система ЛА вычисляет необходимость пребывания в зону ожидания или возможность посадки. Учитывается направления прилёта ЛА, которое влияет на формирование процедуры входа в зону ожидания.

Зональная навигация предполагает применение современных систем самолетовождения и спутниковых навигационных систем с целью выполнения полета без использования наземных средств передачи навигационных данных. Это позволяет на три-четыре километра сократить расстояние, пролетаемое каждым самолетом с момента отрыва и до выхода из зоны аэропорта. Если предположить, что ежедневно выполняются 700 вылетов, экономия на сокращении расхода топлива оказывается значительной (рис 3).

Задачами теории массового обслуживания являются анализ и исследование явлений, возникающих в системах обслуживания. Основная задача теории заключается в определении таких характеристик системы, которые обеспечивают заданное качество функционирования, например, минимум времени ожидания, минимум средней длины очереди и т.д.

Время обслуживания – одна из важнейших характеристик, обслуживающих аппаратов (приборов), определяющая пропускную способность системы.

В теории массового обслуживания время обслуживания tобс предполагается случайной вели-

Рис. 1. Общая схема аэропорта

чиной. Причиной этого может быть нестабильность работы приборов, различия параметров, поступающих в систему требований.

Случайная величина tобсполностью характеризуется законом распределения

F(t) = P (tобс < t)

Этот закон определяется путем статистических испытаний. В практике чаще всего исходят из гипотезы о показательном законе распределения обслуживания:

F(t) = 1 - e -mt, где m = 1/ tобс – интенсивность обслуживания, а tобс – математическое ожидание времени обслуживания.

Приведем пример обеспечения заправки ГСМ в аэропорту.

Имеется n бригад по заправке ГСМ m видов

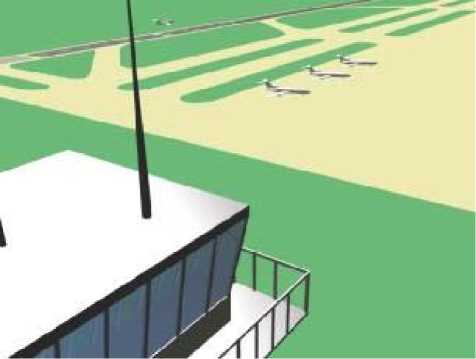
Рис. 2. Модель аэропорта летательных аппаратов, распределенных по различным бригадам. Заправка ГСМ организована силами подвижных бригад, которые могут быть направлены к тому самолету, где есть необходимость в заправке. Суммарное время, необходимое для заправки tз будет состоять из времени tвыз, требуемого для вызова бригады; ее движения к месту заправки tдв; времени осмотра tосми собственно заправки tзап. Полагаем, что время обслуживания – случайная величина с показательным законом распределения и параметром m, где m = 1/ tз .

Для решения определим параметр f=l/m.

Среднее число самолетов, ожидающих заправки

— ож = Z ( k - n ) P .

k = 4

Отсюда средний процент техники, ожидающей заправки в очереди

K ПТР = — • 100% ;

m коэффициент простоя ЛА

K П = N^ • 100% .

n

Среднее число ЛА, находящихся на заправке и в очереди, м =X kPk .

k = 0

Коэффициент простоя техники

, м k = — ^100%.

m

а)                                               б)

Рис. 3. Процедуры вылета с использованием а - без оптимизации траектории вылета, б – с оптимизацией траектории вылета, что увеличивает число коридоров с двух (обведены кружками) до четырех

Далее на основе теории массового обслуживания, проанализируем ситуацию по устранению мелких отказов и неисправностей ЛА. Пусть служба линейного технического обслуживания ЛА имеет n опытных бригад мастеров. В течение рабочей недели от администрации аэропорта поступает заказ на ремонт l ЛА. Общее число ЛА, находящихся в эксплуатации авиакомпаний очень велико, а выходят они из строя (имеют мелкие дефекты) независимо друг от друга. Поэтому имеются основания считать поток заявок пуассоновским. Пусть все бригады мастеров имеют одинаковую квалификацию и в среднем могут отремонтировать k ЛА в день каждая. Определим показатели качества обслуживания в данном аэропорту.

1. Вероятность того, что все бригады мастеров свободны от ремонта ЛА, равна

M

пщ

ож

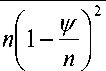
6. Среднее число ЛА, находящихся в службе технического обслуживания

P O

Е К + К к=0 k! Д1 - К) .V n)

2. Вероятность того, что все бригады заняты ремонтом

п =

К Ро nL - — ) .

V n)

3. Среднее время обслуживания каждого ЛА

t обс

.

Ц

4. Среднее время ожидания

t ож

= п

t обс

n - К

nk

M = Mo +Р рУк ■К ож o.

к=1

7. Среднее число бригад, свободных от работы n-1

No = Р, ЕСn - к)К. к=0

Таким образом, подставляя конкретные значения в данные формулы можно определить показатели качество обслуживания любого аэропорта.

А теперь смоделируем работу линейного технического обслуживания (ТО) аэропорта в программе GPSS World Student Version. Предположим, что компания аэропорта нанимает одного мастера, для ремонта ЛА и осуществляет сервисное обслуживание заказчиков, а также делает ремонт “по прибытию”. Ремонт арендованных самолетов, начинается каждые 40±8 часов, работа завершается через каждые 10±1 часов. Ремонт “по прибытию”: замена масла, настройка и корректировка выполняются немедленно. Заказы прибывают каждый 90±10 минут и на данный ремонт уходит 15±5 минут. Заказчики, требующие полного обслуживания, прибывают каждый 5±1 час и требуют ремонта 120±30 минут. Полное обслуживание имеет более высокий приоритет, чем ремонт арендованных самолетов.

Итак, нам нужно определить:

• 1.    Работу мастера в течение 50 дней.

• 2.    Определить загруженность мастера и задержки в обслуживании заказчиков.

5. Средняя длина очереди

Модель представлена в табл. 1.

• *    Модель Работы мастера *

• *    Ремонт арендованных самолетов, выполняются каждую неделю *

• *    Модуль Времени - одна минута *

GENERATE 2400,480,,,1 ;Ремонт арендованных самолетов

QUEUE Overhaul ; Очередь для обслуживания

QUEUE Alljobs ; Сбор общей статистики

SEIZE Maintenance ;получен заказ на ремонт

DEPART Overhaul ;Заказчик уходит из очереди

DEPART Alljobs ; Сбор общей статистики

ADVANCE 600,60   ;Полная работа 10+/-1 часов

RELEASE Maintenance ; Мастер освободился

TERMINATE      ;Удаление одной транзакции

* Ремонт "по прибытии"

GENERATE 90,10,,,3 ;Ремонт "по прибытию"

QUEUE Spot    ; Очередь для ремонта "по прибытию"

QUEUE Alljobs ;Сбор статистики

PREEMPT Maintenance,PR ;Получение заказа

DEPART Spot    ;Уход из очереди ремонта "по прибытию"

DEPART Alljobs ;Сбор статистики

ADVANCE 15,5    ;Время настройки/плавкие элементы/недостатки

RETURN Maintenance ;Освобождает мастера

TERMINATE

• *    Сложный ремонт для заказ чика

GENERATE 300,60,,,2 ;Сложный ремонт самолета

QUEUE Service ; Очередь для обслуживания

QUEUE Alljobs ;Сбор статистики

PREEMPT Maintenance,PR ;Занимает мастера по обслуживанию

DEPART Service ;Уход из сервисной очереди

DEPART Alljobs ;Сбор статистики

ADVANCE 120,30   ;Сервисное время

RETURN Maintenance ;Освобождает мастера

TERMINATE

GENERATE 480    ;Один 8 часовой рабочий день

TERMINATE 1

• *    Счет дней

  Данная программа моделирует работу мастера в течение 50 дней. В результате получаем следующее: мастер был полностью занят на 78 %; среднее время ожидания для ремонта арендованных самолетов 25 дней и 51 день для полного сервисного обслуживания. Не было никакой задержки в работе “по прибытию”. Среднее время ожидания для работ “по прибытию” приблизительно 12 минут.

  Смоделируем вторую ситуацию с помощью GPSS World Student Version . На складе имеется три вида топлива: a) керосин b) бензин и c) дизельное топливо для транспортных средств обслуживания. Для каждого вида топлива имеется свой насос, и запрос обрабатывается для каждо-

  
  

  го вида отдельно. Заказы топлива изменяются от 3000 до 5000 галлонов, в приращении 10 галлонов их распределенных равномерно. Функция исследования – время, требуемое, для заправки.

  • 1.    Производительность работы каждого насоса 6, 5 и 7 минут на 1000 галлонов соответственно.

  • 2.    Число транспортных средств постоянно (время заправки 30 секунд на транспортное средство).

  • 3.    Фиксированное время заправки топливного грузовика две минуты.

  На складе может задерживаться максимум двенадцать грузовиков. Средние время прибытия грузовиков – 18 минут и их

  
  

  Частота .20 .40 .25 .15

  Средний коэффициент обслуживания .45 .60 1.5 2.0

  Наша задача

  • 1.    Смоделировать работу склада ГСМ в течение 5 дней, если число транспортных средств постоянно.

  • 2.    Найти среднее время заправки топливного грузовика.

  • 3.    Какое общее количество топлива продается ежедневно?

  • *    Нефтехранилище

  • *    Модуль Времени - Одна Минута

  Модель представлена в табл. 2.

  В результате расчета были получены следующие значения: средние время заправки грузовика 35 минут, стандартное отклонение приблизительно 14 минут; количество ежедневной продажи горючего = 109490 галлонов.

  Преимуществом имитационных моделей является возможность подмены процесса смены событий в исследуемой системе в реальном масштабе времени на ускоренный процесс смены

  
  

  событий в темпе работы программы. В результате за несколько минут можно воспроизвести работу аэропорта на основе системы массового обслуживания в течение определенного времени, что дает возможность оценить работу в широком диапазоне варьируемых параметров.

  Проводя анализ моделирования однотипных ситуаций с помощью 3D графики Blender и языка моделирования GPSS World Student Version, можно отметить следующее:

  • 1.    Наглядность происходящих процессов в аэропорту хорошо представлена в программе Blender. Управления камерами в данной программе позволяет рассматривать происходящие процессы с разных углов: с диспетчерской вышки, окна администрации, с пассажирского зала и т.д.

  • 2.    Время моделирования 3D графики на персональном компьютере значительно больше, чем в языке GPSS World Student Version.

  • 3.    Отчет по расчетным формулам в программе Blender и отчет в языке GPSS World Student Version совпадают.

  
  

Таблица 2.

RMULT 5631,39941

Arr FUNCTION RN2,C5 ; частота поступлений

0,0/0.2,.45/.6,1/.85,1.5/1.0,2

Pumprate FUNCTION P$Type,L3 ; мин имал ьные значе ния, чтобы перекачать 1000 галлонов 1,6/2,5/3,7

Gals VARIABLE (RN1@201+300)#10

Type VARIABLE RN1@3+1

Pump VARIABLE (FN$Pumprate#P$Gals)/1000+S$Depot/2+2

Depot STORAGE 12      ;Максимальный участок памяти для 12 топливных грузовиков

Transit TABLE M1,10,10,20   ;Время работы топливных грузовиков

Qty TABLE X$Gals,20000,20000,9 ;Количество нефти в данный день

GENERATE 18,FN$Arr ;Приезд топливн ого грузовика

ASSIGN Gals,V$Gals ;P$Gals=количеству галлонов

ASSIGN Type,V$Type ;P$Type=тип горючего

ENTER Depot QUEUE P$Type SEIZE P$Type DEPART P$Type

ADVANCE V$Pump

;топливный грузовик приезжает в нефтехранилище

;Очередь по типу горючего

;Работает насос

;Очередь продвигается на одного

;Сервисное время работы насоса

RELEASE P$Type ;Освобождает насос

LEAVE Depot ; Топливный грузовик уезжает из нефтехранилища SAVEVALUE Gals+,P$Gals ;Счетчик остановлен. Галлон топлива продан TABULATE Transit   ;Таблица текущего врем ени

TERMINATE       ;Грузовик уезжает

GENERATE 480     ;Время заправки в один день

TABULATE Qty     ;Записи нет. Галлон топлива продан

SAVEVALUE Sold+,X$Gals ;Запись общей продажи топлива SAVEVALUE Gals,0 ;Обнуление продажи TERMINATE 1      ;Один день пр ош ел