Вязкопластическое деформирование гранулированного никелевого сплава при высоких температурах

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN

Авиационное двигателестроение является крупным потребителем сложнолегированных, в том числе порошковых (гранульных), сталей и жаропрочных сплавов на никелевой и титановой основе, которые трудно поддаются обработке давлением. Поэтому, для формообразования из них заготовок дисков газотурбинных двигателей (ГТД) 5-го и 6-го поколения требуется разработка новых технологических процессов. Перспективными в этом отношении являются ротационные методы, которые существенно снижают силы деформации, позволяют получать детали сложной пространственной формы и существенно повышают коэффициент использования металла [1; 2].

В процессе изотермической раскатки в условиях высокой температуры материал подвергается вязкопластическому деформированию. При этом процесс деформирования материала в зависимости от вращения диска и движения ролика может повторяться. Напряженное состояние материала в процессе раскатки является неоднородным и многоосным. К тому же диаграмма вязкопластического деформирования материала при растяжении с различными скоростями деформирования после начального упрочнения имеют падающий участок разупрочнения вплоть до разрушения. Такое поведение материала обусловлено тем, что при высоких темпера- турах наблюдается кратковременная ползучесть, происходящая в условиях мощного разупрочнения.

Экспериментальному исследованию и математическому моделированию процессов термовязкопластического деформирования конструкционных сталей и сплавов посвящено большое количество работ [3–33]. Наиболее развитыми и перспективными направлениями математического моделирования термовязкопластического деформирования являются варианты теории термовязкопластичности, базирующиеся на теории течения при комбинированном упрочнении [8–17; 21–29].

В работе рассматривается вариант теории термовязкопластичности, основанный на теории неупругости [9]. Вариант теории термовязкопластичности обобщен на неизотермическое нагружение и на зависимость процесса нагружения от скорости деформирования. Определены материальные параметры варианта теории термовязкопластичности, базовый эксперимент и метод определения материальных параметров. Для гранулированного никелевого сплава получены материальные параметры для высоких температур. Проводится экспериментально-теоретическое исследование вязкопластического поведения гранулированного никелевого сплава при одноосном растяжении в условиях высоких температур в широком диапазоне скоростей деформирования. Результаты расчетов сравниваются с данными экспериментов.

1. Основные положения и уравнения варианта теории термовязкопластичности

Материал однороден и начально изотропен. В процессе вязкопластического деформирования в нем может возникать только деформационная анизотропия. Тензор скоростей деформаций ly представляется в виде суммы тензоров скоростей упругой ej и неупругой ep деформаций e y = e e + e P.                       (1)

Процесс деформирования зависит от изменения температуры T и скорости деформирования £

; = [ з e y e ,                   (2)

где e y - девиатор скоростей деформации.

При изменении напряжений, температуры и скорости деформирования упругие деформации следуют закону Гука, обобщенному на неизотермическое нагружение и нагружение при переменной скорости деформирования eej = EI °i - V(3°05i - °7i )] + aT T + a ^’     (3)

a ^T = a_T 8 —1- [ c -v(3a_n8 -a )]—-—(3a_n8 -a ,

У T V E 2 L       \ ⁰ i ^jv) d d T EV ⁰ J "'TT

a ^; —1— [о. -v(3a_n5 -a-)]—-—(3a_n8. -a    ,

1    E 2 L \°v j d^ EV 0 y jy) g^ , где Gy - тензор напряжений; a0 = au / 3 - среднее напряжение; 5y - символ Кронекера; E - модуль Юнга; V - коэффициент Пуассона.

Полагается, что в пространстве составляющих тензора напряжений существует поверхность нагружения, разделяющая области упругого и неупругого состояний. Поверхность нагружения изотропно расширяется или сужается и смещается в процессе нагружения. Уравнение поверхности нагружения принимается в следующем виде:

f ( ° y ) = 2 ( s y ^- a y )( s y ^- a y ) ^- C = 0.        ⁽⁴⁾

Здесь s * = S y - a ij - девиатор активных [4] напряжений; s_ij - девиатор напряжений. Тензор a_ij (добавочных напряжений [6], остаточных микронапряжений [4]) характеризует смещение поверхности нагружения в деви-аторном пространстве напряжений, т.е. направленное (анизотропное) упрочнения. Скаляр C отвечает размеру (радиусу) поверхности нагружения и характеризует изотропное упрочнение (разупрочнение). Тензор a_y

и радиус C являются функционалами процесса нагружения.

Для радиуса поверхности нагружения принимается следующая зависимость:

C = C p (С , T , ; ) ,                 (5)

C = q e ^{e p} * + q T T + q ^.               ⁽⁶⁾

Здесь e p *

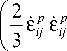
- интенсивность скоростей

неупругой деформации (скорость накопленной неупру

гой деформации);

Е2 ) 2

e p = fl -e p e p I dt u ∗            ijij

0 V ³        /

накопленная

неупругая деформация (длина дуги траектории неупругой деформации); q _e , q_T , q ; - определяющие функции, которые далее будут выражены через материальные.

Смещение поверхности нагружения определяется эволюционным уравнением Армстронга - Фредерика -Кадашевича [19; 20], обобщенным на неизотермическое [9] нагружение и переменную скорость деформирования

a l ij = 3 g ^e P ⁺ g a a ij ^e u * ⁺ gaa ij^{T +} g^ y .        ⁽⁷⁾

Здесь g , g_a , g T , g ^; - определяющие функции, которые выражаются [9] через материальные функции в и a _a следующим образом:

о            о Т 1 Э°я Е 1 Эоя g = в° а , ga =-в ga =™    , g;=--

σ _a ∂ T       σ _a ∂

.

Неупругие деформации являются функционалами процесса нагружения и определяются на основе ассоциированного с поверхностным нагружением (4) закона течения (градиентального закона течения) следующим образом:

*                             1

— p df л 3 Sy pF _* l 3 * * 12 ey = 4 ^ = V Teu * , °u = I Tsy sy I da у    2 °u          V2    J)

.

Здесь ° U - интенсивность активных напряжений; Z - скалярная функция.

Скорость накопленной неупругой деформации при мягком (задаются компоненты тензора напряжений) и жестком (задаются компоненты тензора деформаций) режимах нагружения определяется [9] следующим образом:

* l

ё_м '. = — ³ ^ j -T j - B^Ti’ - B ^;;

^u * E * 2 a *             ^s

^p ε _{u ∗}

E + 3 G ∗

_{3 G} ^SiJ ( ^e ij ^-a "y T ^-a l ^; )

σ ^∗ _u

-

BTi^ - b ^;; ,

^E * = q e ⁺ g ⁺ g a a U ,

B^T = q j ⁺ gX

EE *

B ^E = q e ⁺ g ; ^au ,

*

3 5 a

* J 1111

a = —-—-u**

2 ° u .

Уравнение (9) соответствует мягкому нагружению, а уравнение (10) – жесткому.

Условия упругого и неупругого состояний следуют из того, что для неупругого состояния необходимо, чтобы изображающаяся точка процесса нагружения находилась на поверхности нагружения и определяемая скорость накопленной неупругой деформации была положительная, а упругое состояние следует при нарушении любого из двух упомянутых условий. Тогда условия упругого и неупругого состояний будут иметь следующий вид:

° U <  C U e " . 5 0 - упругость, о U = C П e Up * > 0 - неупругость.

Здесь под e Up * подразумевается выражение, задаваемое уравнением (9) либо (10) или любым другим уравнением, связывающим скорость накопленной неупругой деформации и любой набор скоростей напряжений и деформаций (смешанное нагружение).

• 2.    Материальные функции и их аппроксимации

Рассмотренный вариант теории термовязкопластичности замыкается следующими материальными функциями:

E ( T , E ) , v , a _T ( T ) - упругие функции;

C p ( e P , T , E ) - функция изотропного упрочнения;

о _a ( T , E ) , в - функции анизотропного упрочнения.

Эти функции предлагается аппроксимировать следующими выражениями:

E(T, E) = KE (T)EnE(T) ,(12)

Cp (ep*, T,E) = Ec (T)ep* + Cо (T,E) ,(13)

со ( t , E) = Kc (T )EnC (T),(14)

° a ( T, E) = Ka ( T )Ena (T) ,(15)

^{d C}P _F      ^{d C}P dE_cP ^CC

qP = = Er , qT = = e,P + , e dep C d T dT u dT u *

= d C p =э с^ q ^E    dE dE .

Таким образом, на основе результатов экспериментов необходимо определить следующие материальные параметры:

K_E ( T ) , n_E ( T ) , v , a _T ( T ) - параметры аппроксимации упругих функций;

E_C ( T ) , K_C ( T ) , n_C ( T ) - параметры аппроксимации функции изотропного упрочнения;

K_a ( T ) , n_a ( T ) , в - параметры аппроксимации функций анизотропного упрочнения.

Экспериментальные исследования, проведенные авторами работ, показали, что изменение материальных функций v и в от температуры и скорости деформирования незначительно.

• 3.    Метод определения материальных параметров

• 4.    Вязкопластическое деформирование гранулированного никелевого сплава

  Для выбора модели поведения гранулированного никелевого сплава и определения материальных параметров необходимо провести ряд экспериментов по одноосному растяжению образцов (см. рис. 1) в диапазоне температур, до которых может быть нагрета заготовка при проведении раскатки . Для получения достоверной диаграммы деформирования материала замер деформации осуществляется по перемещению захватов испытательной машины, отнесенному к длине рабочей части образца, измеряемой между серединами радиусов перехода от рабочей части к захватной. Испытания образцов проводятся при температурах 1050,1100,1150 ° C и скоростях деформирования 0,032; 0,0053; 0,00053; 0,00026; 0,00011 c ^{- 1} .

Метод определения параметров гранулированного никелевого сплава основан на представлении экспериментальных данных в виде линейных зависимостей с использованием метод наименьших квадратов. Материальные параметры сплава определяются при разных температурах. Исходными данными для определения материальных параметров сплава является диаграмма, связывающая нагрузку, приложенную к образцу (рис. 1), его удлинение, начальный диаметр образца, база, на которой проводится измерение удлинения, и заданная скорость удлинения образца. Полученные по результатам эксперимента диаграммы перестраиваются в истинные диаграммы деформирования, связывающие истинное напряжение и логарифмическую деформацию для каждой температуры и разных скоростей деформирования.

Модуль упругости определяется как тангенс угла наклона начального (упругого) участка диаграммы деформирования. Далее в логарифмической системе координат строится линейная зависимость lg E от lg E и определяются параметры K_E и n_E для каждой температуры.

Для определения скорости изотропного разупрочнения E_C диаграмма деформирования перестраивается в диаграмму неупругого деформирования, исключая упругую деформацию. На построенных диаграммах неупругого деформирования присутствует линейный участок, тангенс угла наклона которого и есть скорость изотропного разупрочнения E_C .

Начальный размер поверхности нагружения C ₀ определяется напряжением, разделяющим область упругого и неупругого деформирования, значение которого можно определить путем экстраполяции первых точек диаграммы неупругого деформирования до нулевой деформации. Далее в логарифмических координатах строится линейная зависимость lg C ₀ от lg E и определяются параметры K_C и n_c для каждой температуры.

Для определения параметров анизотропного упрочнения о a и р из диаграммы неупругого деформирования вычитается функция (13) изотропного разупрочнения, и получается диаграмма изменения микронапряжений от неупругих деформаций. Далее полученная диаграмма перестраивается в координатах производной микронапряжения da / d г p от микронапряжения a . Аппроксимируя эту зависимость линейной функцией, можно получить [9] параметры о _a и р . Далее в логарифмических координатах строится линейная зависимость lg о _a от lg ^ и определяются параметры K_a и n_a .

В таблице приведены материальные параметры гранулированного никелевого сплава для трех уровней высоких температур. Для данных, приводимых в таблице, скорость деформирования ^ измеряется в c ^{- 1} .

Материальные параметры гранулированного никелевого сплава

Material parameters of granular nickel alloy

Параметр	Значение
Т , °С	1050	1100	1150
K , МПа E	14000	14000	12000
nE	0.0756	0.113	0.138
KC , МПа	745	456	255
nC	0.166	0.166	0.166
EC , МПа	-1600	-1600	-780
Ka , МПа	196	165	92
n a	0.16	0.17	0.173
р	250	250	250
V	0,3	0,3	0,3

Экспериментальные диаграммы деформирования при разных температурах и скоростях деформирования приведены на рис. 2–4.

Результаты испытаний образцов на растяжения с разгрузкой и последующим растяжением со скоро- стью деформирования 0,032 c 1 приведены на рис. 5-7 для разных температур. Экспериментальные результаты на рис. 2–7 показаны кружками различного цвета.

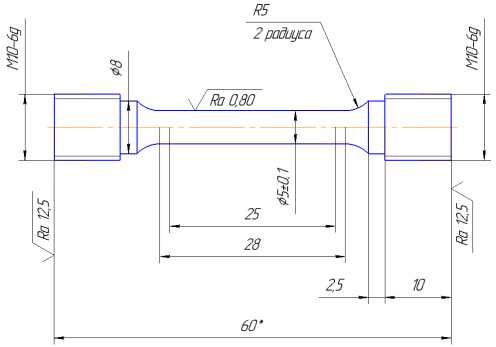
Рис. 1. Образец для испытаний при повышенных температурах

Fig. 1. Specimen for testing at elevated temperatures

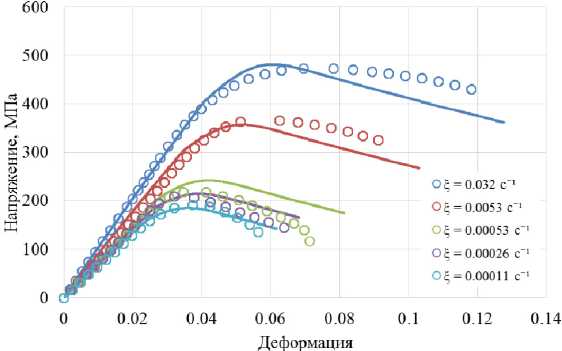
Рис. 2. Расчетные и экспериментальные диаграммы деформирования гранулированного никелевого сплава при температуре 1050 °С

• Fig. 2.    Calculated and experimental diagrams of deformation of a granular nickel alloy at a temperature of 1050 °С

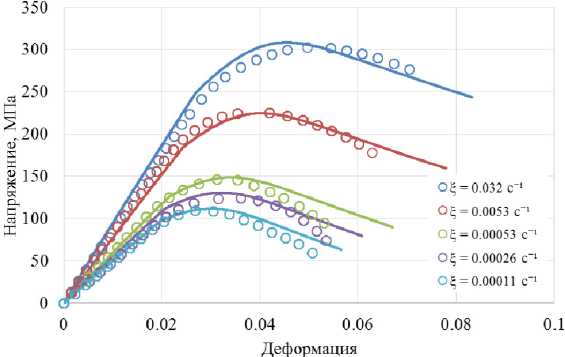
Рис. 3. Расчетные и экспериментальные диаграммы деформирования гранулированного никелевого сплава при температуре 1100 °С

• Fig. 3.    Calculated and experimental diagrams of deformation of a granular nickel alloy at a temperature of 1100 °С

  

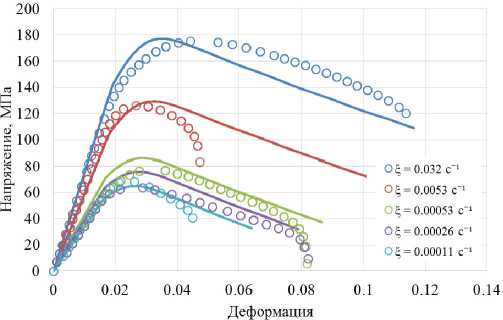
  Рис. 4. Расчетные и экспериментальные диаграммы деформирования гранулированного никелевого сплава при температуре 1150 °С

  
  
  

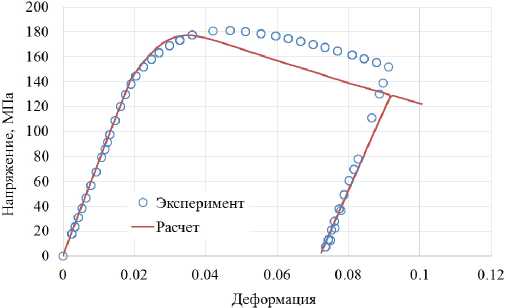
  Рис. 7. Расчетная и экспериментальная диаграмма деформирования гранулированного никелевого сплава при температуре 1150 °С с разгрузкой

  
  

• Fig. 4.    Calculated and experimental diagrams of deformation of a granular nickel alloy at a temperature of 1150 °С

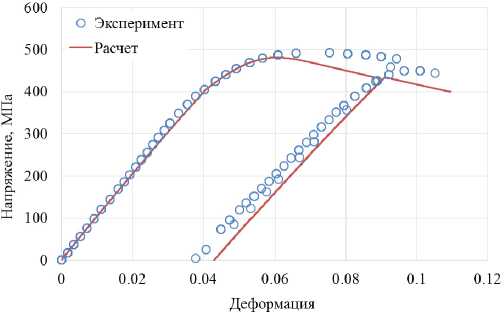
Рис. 5. Расчетная и экспериментальная диаграмма деформирования гранулированного никелевого сплава при температуре 1050 °С с разгрузкой

Fig. 5. Calculated and experimental diagram of deformation of a granular nickel alloy at a temperature of 1050 °С with unloading

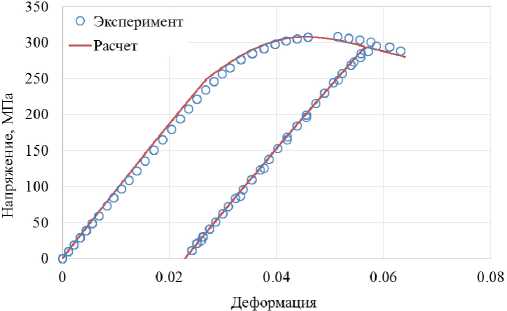
Рис. 6. Расчетная и экспериментальная диаграмма деформирования гранулированного никелевого сплава при температуре 1100 °С с разгрузкой

Fig. 6. Calculated and experimental diagram of deformation of a granular nickel alloy at a temperature of 1100 °С with unloading

Fig. 7. Calculated and experimental diagram of deformation of a granular nickel alloy at a temperature of 1150 °С with unloading

Для расчетного определения напряженно-деформированного состояния при одноосном деформировании по заданной скорости осевой деформации и температуре решается задача Коши для системы уравнений для одноосного напряженного состояния при жестком нагружении, полученной на основе общих уравнений, приведенных выше. Пример получения такой системы уравнений приводится в работе [9]. Решение задачи Коши проводится по методу Рунге – Кутты 4-го порядка точности.

На рис. 2–7 сплошными кривыми различного цвета показаны результаты, полученные на основе предложенного варианта теории вязкопластичности. Сравнение результатов расчетов и экспериментов показывает, что расчет качественно моделирует нестандартное поведение падающих диаграмм растяжения при различных скоростях деформирования и температурах. Поведение материала в экспериментах при упругой разгрузке и последующем нагружении соответствует рассчитанному с помощью модели поведения материала. Отличие результатов расчетов и экспериментов не превышает 15 %.

Заключение

Сформулированы основные положения и уравнения варианта теории термовязкопластичности для математического моделирования процесса раскатки дисков из гранулированного никелевого сплава. Разработан метод идентификации материальных параметров, замыкающих вариант теории термовязкопластичности. Получены материальные параметры гранулированного никелевого сплава.

Результаты проведенного математического моделирования удовлетворительно коррелируют с результатами экспериментов, что говорит об адекватности предложенного варианта теории термовязкопластичности и метода идентификации материальных параметров.