Вязкоупругие свойства полимерных жидкостей и их смесей

Полимерные жидкости находят широкое применение в современной технике. Большой интервал рабочей температуры и хорошие смазывающие свойства позволяют применять их в качестве консистентных смазок, приборных масел, полирующих средств, а также в качестве гидротормозных жидкостей. Поэтому изучение физико-механических и химических свойств полимерных жидкостей и их смесей открывает новые области исследований для решения практических задач. Полимерные жидкости – это новая группа жидкостей, которая в силу своего особого строения должна обладать некоторыми свойствами, отличными от свойств простых жидкостей. Эти жидкости отличаются от простых тем, что состоят из молекул, состоящих в свою очередь из большого количества атомов и, следовательно, имеющих большое количество внутренних степеней свободы, позволяющих в случае линейных цепочек изгибаться в определенных пределах вплоть до образования клубков.

Большое внимание уделяется исследованию природных полимеров. В частности, коллагену [1], который является одним из наиболее распространенных в природе высокомолекулярных соединений. Простейшими структурными элементами коллагена являются цепи, объединяющие большое число различных остатков амино- или иминокислот; цепи соединены между собой пептидными связями. Установлено, что по длине полипептидных цепей коллагена правильно чередуются: 1) менее полярные участки (блоки), образованные из остатков иминокислот (пролина и оксипролина) и гликоля; 2) более полярные участки, которых много остатков карбоновых и диаминокислот. Таким образом, коллаген является природным блоксополимером. В соединительных тканях животных коллаген всегда присутствует в совокупности с различными веществами, например, с полисахаридами, образуя белково-углеводные комплексы. Полисахариды – природные биополимеры, содержащие цепи, образованные остатками моносахаридов.

В данной работе акустическим резонансным методом исследованы вязкоупругие свойства гомологического ряда полиэтилсилоксановых жидкостей (ПЭС), которые представляют собой либо смесь полимеров линейной (C 2 H 5 )Si-O-[Si(C 2 H 5 ) 2 O] n -Si(C 2 H 5 ) 3 и циклической [(C 2 H 5 ) 2 SiO] n структур, либо полимеры линейной структуры.

Также были исследованы смеси таких полимеров, как коллаген и карбоксиметилцеллюлоза (КМЦ). КМЦ – полисахарид, содержащий остатки глюкозы. Смешение полимеров во многом аналогич- но сополимеризации как способу достижения заданных свойств химических структур. Разница состоит в том, что смешение позволяет достичь этой цели физическим, а не химическим путем.

Суть акустического резонансного метода заключается в следующем [2]. Пьезокварцевый кристалл, колеблющийся на основной резонансной частоте, контактирует своей горизонтальной поверхностью, совершающей тангенциальные смещения, с прослойкой жидкости, накрытой твердой накладкой, расположенной на одном конце. При этом прослойка жидкости испытывает деформации сдвига и в ней устанавливаются стоячие сдвиговые волны. В зависимости от толщины прослойки жидкости изменяются параметры резонансной кривой пьезокварца, по которым определяются действительный модуль сдвига G ’ и тангенс угла механических потерь tg θ .

Теория акустического резонансного метода дает следующие выражения для G ’ и tg θ [3]:

G ' =

4 π ² Mf 0 Δ f ' H _;

G ''    Δ f ''

tg θ == ,

G '     Δ f '

где М – масса пьезокварца, Δ f' и Δ f" - действительный и мнимый сдвиги резонансной частоты, S – площадь основания накладки, f 0 – резонансная частота пьезокварца. Мнимый сдвиг Δ f" равен половине изменения ширины резонансной кривой. В эксперименте измеряются толщина прослойки жидкости H и сдвиги резонансной частоты. По формулам (1) вычислялись основные вязкоупругие параметры жидкостей. В эксперименте применялся пьезокварц Х-18,5⁰ среза с резонансной частотой 74 к Гц, с массой 6,24 г, площадь основания накладки составляла 0,2 см².

Из выражений (1) видно, что при наличии комплексного модуля упругости зависимости Δ f' и Δ f" от обратной величины толщины жидкой прослойки должны быть линейными.

На рисунке 1 показаны экспериментальные результаты для ПЭС жидкостей с различными значениями n . По оси абсцисс отложены обратные величины толщины жидкой прослойки, по оси ординат – действительный сдвиг резонансной частоты. Аналогичные линейные зависимости получаются и для Δ f ″ .

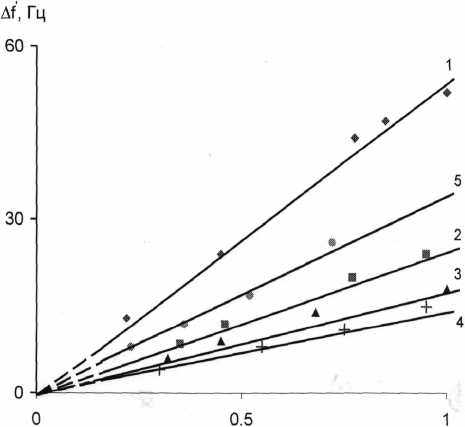
1/Н, мкм"1

Рис. 1. Зависимость действительного сдвига частоты Δ f' от обратной величины толщины прослойки жидкости Н для ПЭС-1 (1), ПЭС-2 (2), ПЭС-3 (3), ПЭС-4 (4) и ПЭС-5 (5)

Рассчитанные значения G ’ и tg θ приведены в таблице 1. В таблице также приведены значения табличной и эффективной вязкости, рассчитанной по реологической модели Максвелла:

η = G '(1 + tg ² θ )

.

^М    2 π f ₀ tg θ

Анализируя данные таблицы, можно заметить существенное отличие вязкоупругих свойств полиэтилсилоксановых жидкостей от полиметилсилоксановых (ПМС) жидкостей [4-6]. Если у ПМС жидкостей с увеличением молекулярной массы или n действительный модуль сдвига G′ растет, то у ПЭС- жидкостей G' сначала уменьшается и, проходя через минимум, вновь возрастает. ПМС жидкости с большими числами n обладают большим конформационным набором, т.е. полимерные цепи могут принимать больше различных пространственных форм, легче свертываться, что ведет к увеличению модуля сдвига. ПЭС жидкости, вероятно, при малых п более структурированы, молекулы более компактны, упорядочены, с возрастанием п увеличивается количество степеней свободы, степень упорядоченности молекул при этом уменьшается, что выражается в уменьшении G’. В дальнейшем удлинение звеньев цепочки ведет к увеличению конформационного набора, молекулы ПЭС способны зацепляться друг за друга с образованием межмолекулярных связей, что ведет к увеличению модуля сдвига.

Таблица 1

Вязкоупругие характеристики полиэтилсилоксановых жидкостей

Жидкости	t°С	G ’ - 10 -6 дин/см2	tgθ	η T , П	η М , П	число атомов Si в цепи
ПЭС-1	23	9.83	0.11	0.03	194.48	2
ПЭС-2	24	4.81	0.63	0.12	23.2	3
ПЭС-3	24	3.45	0.87	0.14	15.16	4
ПЭС-4	23	2.96	2	0.46	16.1	5
ПЭС-5	24	5.9	6.6	3.88	86.69	15

Изменение тангенса угла механических потерь с увеличением молекулярной массы у этих жидкостей проявляется по-разному. У ПМС-жидкостей он проходит через максимум, оставаясь при этом меньше 1, для ПЭС-жидкостей возрастает, достигая значений больше единицы. Согласно реологической модели Максвелла частота релаксации наблюдаемого процесса приближается к частоте эксперимента, проходит через нее и в дальнейшем уходит в область высоких частот.

При исследовании смеси природных полимеров сначала были определены значения модуля упругости и тангенса угла механических потерь для исходных компонентов смеси (2% водные растворы коллагена и КМЦ). Значения действительного модуля низкочастотной сдвиговой упругости оказались равны 0,65 - 10 6 дин/см² и 0,8 - 10 6 дин/см² для коллагена и КМЦ соответственно. Затем исходные компоненты смешивались в различных соотношениях и определялись те же параметры.

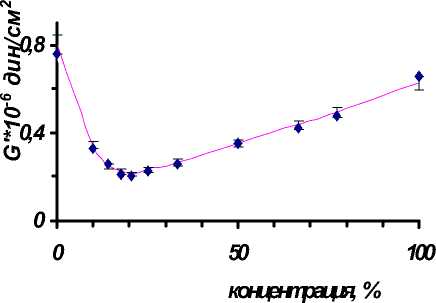
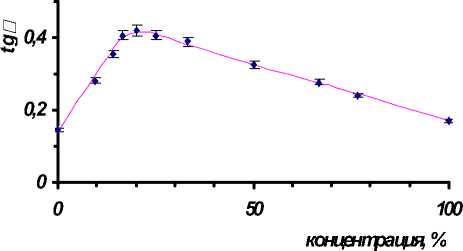
Рис 2. Зависимость G’ от концентрации КМ 74 Г

Рис 3. Зависимость tgθ от концентрации коллагена в КМЦ при 74 кГц

На рисунке 2 представлены результаты исследования свойств данной смеси. По оси абсцисс отложено содержание КМЦ в коллагене, выраженное в процентах. Видно, что G ’ проходят через минимум при содержании 80% КМЦ и 20% коллагена, а tg θ проходит через максимум при этом же составе смеси (рис.3).

А по модели Такаянаги [7], в которой поведение смеси, состоящей из двух компонентов с различными модулями упругости, справедливо соотношение:

G = G , ^ 1 G 1 + ( a + У 2 ) G 2 см ¹ (1 + a(p 2 ) G 1 + аф 1 G 2’

где G 1 и G 2 – модули упругости компонентов, φ 1 и φ 2 – объемные доли компонентов в смеси. Из формулы (3) видно, что для такой модели модуль упругости смеси будет равномерно увеличиваться от G 1 до G 2 . В модели предполагается, что смесь является чисто механическим соединением компонентов ( α = 0). Исходя из экспериментальных результатов исследования смеси коллагена и КМЦ, можно предположить, что их молекулы взаимодействуют между собой. При определенном составе смеси наблюдается минимум взаимодействия молекул и смесь является менее упругой, но более пластичной, поэтому наблюдается минимум модуля упругости.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 09-02-00748-a.