Влияние аддитивных составляющих на фазовые шумы делителя частоты в составе цифрового синтезатора частот

Построение современных средств цифровой радиосвязи, радиолокации, измерительного оборудования невозможно без использования синтезатора частот. От качества генерируемого синтезатором сигнала во многом зависят характеристики и возможности всей системы, и в ряде случаев именно он является ограничивающим фактором, особенно на частотах выше 2–3 ГГц, когда работа с сигналом требует особых приемов и материалов, свойственных СВЧ-технике. Ниже речь пойдет об эффектах, имеющих место при высокочастотном цифровом синтезе, хотя аналогичные методы можно применить и для низкочастотной области.

Рис. 1. Синтезатор частот

В состав практически любого синтезатора наряду с такими элементами, как ГУН (VCO), фазовый детектор (Phase Detector), зарядовый насос (Charge Pump), петлевой фильтр (Loop Filter) и направленный ответвитель (Directional Coupler), входит цифровой делитель частоты (Frequency Divider, Prescaler) (рис. 1.).

Каждый из этих элементов вносит свой вклад в результирующий фазовый шум на выходе синтезатора. Общепринятая оценка шума на выходе такой системы складывается из влияния опорного генератора, фазового детектора, петлевого фильтра и ГУНа. Математические выражения, связывающие эти параметры, методика расчёта и измерения довольно подробно описаны в литературе по данной тематике [1, 2]. Влиянием делителей в большинстве случаев пренебрегают, поскольку сами по себе они не вносят существенных искажений, их собственный шум по отношению к опорному сигналу низок, а передаточная характеристика по фазе линейна. Однако не стоит забывать, что в реальных системах помимо собственных источников шума компонентов синтезатора существуют внешние источники излучения, которые способны значительно повлиять на конечный результат.

Высокочастотные наводки на петлевой фильтр сказываются слабо, поскольку выход зарядового насоса и вход ГУНа, как правило, шунтированы керамическими конденсаторами. Связи между блоками, обведёнными на рис. 1 пунктирной линией, достаточно малы, так как обычно размещены в одном корпусе микросхемы

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 и практически не образуют контуров и соответственно менее подвержены внешнему излучению. Наиболее подверженными излучению участками являются связи между опорным генератором и входным делителем опорной частоты, а также направленным ответвителем и входом делителя сравниваемой частоты. Причиной этого является высокий (порядка нескольких сотен) коэффициент передачи по фазе от этих точек до выхода, равный N/R в области пропускания петлевого фильтра.

Аддитивный шум, наведённый на вход опорной частоты, после прохождения через цифровой делитель преобразуется в фазовый шум, дальнейший анализ которого производится известными методами [3]. Темой же данной работы является анализ преобразования аддитивного шума в фазовый на выходе делителя и его спектральных составляющих при входных воздействиях, находящихся в частотном диапазоне гораздо выше частоты сравнения фазового детектора. Результатом анализа является методика оценки спектральных характеристик фазового шума на выходе делителя и методы борьбы с такого рода эффектами.

• II.    Модель преобразования аддитивного шума в фазовый

Рассмотрим модель, показанную на рис. 2. В нее входит опорный генератор детерминированного периодического сигнала s ( t ), генератор шума, представленного в виде случайного процесса f ( t ), сумматора, компаратора и цифрового делителя.

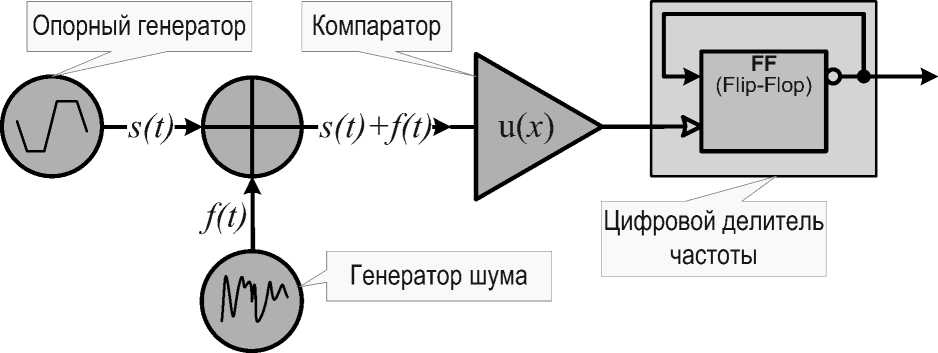
Рис. 2. Модель преобразования аддитивного шума в фазовый

Генератор шума и сумматор соответствуют модели аддитивного шума, наведённого на линию связи между генератором опорной частоты и входом делителя частоты в микросхеме цифрового фазового детектора (рис. 1). Компаратор представляет входной каскад делителя частоты в этой микросхеме, он сравнивает входной сигнал с нулем и выдает логический сигнал «0», если сигнал на входе меньше нуля, и «1», если больше либо равен нулю, то есть компаратору можно сопоставить единичную функцию Уолша. В качестве цифрового делителя частоты приведён делитель на два. Фактически он состоит из двухтактного триггера, работающего по фронту (flip-flop), с инвертированным выходом, замкнутым на его вход.

Опорный генератор выдает синал s ( t ) с периодом T s и конечной скоростью нарастания фронта в точке пересечения с нулем. Таким образом, если исключить шум, то на выходе компаратора будем иметь периодический сигнал с фронтами (моментами переключения из «0» в «1»), расположенными во времени строго через интервалы T s . Если добавить шум (подразумевается, что уровень шума гораздо ниже уровня опорного сигнала), то моменты времени, в которые функция s ( t ) + f ( t ) проходит через ноль, сместятся относительно своих номинальных точек. Эти смещения с учётом прохождения через делитель частоты и есть тот фазовый шум, который следует рассмотреть.

• III.    Спектральная плотность средней мощности фазового шума

Для облегчения анализа разобьём задачу на следующие этапы:

• —    рассмотрим фазовый шум, то есть временные смещения фронтов как непрерывный во времени случайный процесс, и найдём его спектральную плотность средней мощности;

• —    преобразуем непрерывный процесс в ряд временных отсчётов;

• —    рассмотрим влияние цифрового делителя частоты.

• III.1. Спектральные характеристики фазового шума как непрерывного процесса во времени

Аналитическая оценка. Для определения непрерывного во времени смещения представим, что фронт сигнала s ( t ) может непрерывно двигаться по оси времени, и рассмотрим одну из реализаций случайного процесса f ( t ) (рис. 3).

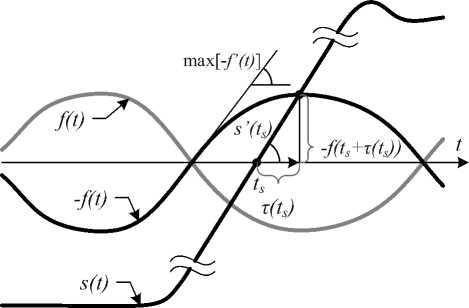
Рис. 3. Графическое представление фазового сдвига

На рис. 3 s(t) пересекает ноль в точке ts — это положение фронта в идеальном случае. В случае с шумом указанное положение определяется пересечением s (t) и —f (t). Сдвиг будет равен разности точки пересечения и ts . Этот сдвиг как функцию параметра ts назовем т (ts) — он является реализацией исследуемого случайного про- цесса.

Сделаем следующие предположения об опорном сигнале s (t) и шуме f (t):

• 1)    процесс f ( t ) ограничен, то есть

  < го : f min < f ⁽ m ) ( t )

  
  

  3 ^f min ,

  
  

  f max

  
  

  max ,

  
  

Vm, t, где f(m) (t) — m-я реализация процесса f (t) и E(f(m)(t)) = 0, где f(m)(t) — m-я реализация процесса f (t), E — опера- тор усреднения по всем реализациям;

• 2)    функция s ( t ) дифференцируема и V s E [min( f ( t ));max( f ( t ))] , ^ t, t s E R выполняется условие

s — s (ts + SEltS)) s (ts + s'ltS))

< 1;

• 3)    процесс f ( t ) стационарен в широком смысле, то есть для функции плотности вероятности выполнены условия

P ^{( f} 1 ; t 1 ) = P ^{( f} 1 ; t 1 + ^т ) ^,Vt

и

P ^{( f} 1 ^,f 2 ; t 1 ,t 2 ) = p ^{( f} 1 ^,f 2 ; t 1 + ^T,t 2 + ^T ) ^,Vt ;

4) процесс f ( t ) дифференцируем в среднеквадратическом, то есть

3f-(t):1Н„ e[(Z ('') - f ('')(t) -

С учётом приведённых выше ограниче-гний найдём связь между реализацией f ( t ) и реализацией т ( t ). Обозначив s' ( t _s ) через K s и воспользовавшись выражением (1), напишем

- f ' ( t )} = 0 .

где f ^{( m} ) ( t ) — m -я реализация процесса f ( t ), E — оператор усреднения по всем реализациям;

f ( t s + т ( t s )) + K s T ( t s ) = 0 .      (3)

Разложив реализацию f ( t ) в степенной ряд до первого члена в точке t _s с учётом выражения (2), получим

f ( t s ) + f ( t s ) • т ( t s ) + K s T ( t s ) = 0 .

^{T (} t s ) =

^{f (} t s )

Ks+ dt(ts)

В условии 1 требование на равенство нулю среднего значения не является существенным ограничением, поскольку это всего лишь приводит к постоянному сдвигу по фазе и соответственно может быть приведено к процессу с нулевым средним путём пересчёта рабочей точки пересечения фронта.

Условие 2 означает линейность участка фронта опорного сигнала в области точки пересечения с нулем. В реальных устройствах при отсутствии серьезных ошибок при проектировании это всегда выполняется, поскольку существует ограничение на немонотонность опорного сигнала в области границ переключения.

Условия 3 и 4 являются обычными при использовании корреляционного подхода. Большинство реальных процессов, встречающихся в цифровой связи, им удовлетворяют.

Условие 5 означает отсутствие двойных переключений и возможность интерполяции реализации процесса f ( t ) в области точки t _s . Знак «много больше» в условии 5 служит лишь для большей точности оценки. Для сходимости результата вполне достаточно знака «больше». Очевидно, если данное условие не будет выполняться, возникнут двойные переключения, что совершенно не приемлемо для физических систем, и рассматривать этот случай вообще не стоит.

При практическом использовании для большинства встречающихся сигналов эти условия можно заменить одним: уровень опорного сигнала должен быть гораздо выше уровня шума.

Ввиду малости производной реализации f ( t ) по отношению к K _s разложим знаменатель в ряд до первой степени:

^{T (} t s ) =

f(ts) (

K s k

-

f ' ( t s ) k

Ks.

Выражение (4) будем в дальнейшем использовать для нахождения спектральных характеристик процесса т ( t _s ). Для этого определим спектральную плотность средней мощности и выразим её через оператор усреднения по реализациям во временной области. Поскольку в выражение (4) входит производная, то свяжем усреднение по реализациям производных с производными от усреднённого значения.

Итак, пусть имеется m -я реализация f ^{( m} ) ( t ) случайного процесса f ( t ). Обозначим через f,' ) ( t ) функцию

f(')m _ f f(')(t). |t| < , fT (t} = to. Iti > , .

тогда её фурье-образ назовем F,(') (ju). При этом спектральная плотность средней мощности равна фf(u) = ^lim 1 E ( FT')(ju) ) . (5) 2nT^^T у J

где E — оператор усреднения по реализациям. Перейдём в выражении (5) к временной области.

E (4')(ju)FT')• (ju)) =

T

⁺ 2

= J J B ( т.т - t ) dт

e-titdt.

^

T

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 тогда

+ОО

Ф f ( ш ) = 1- [ B ( т )■ dr,

2 п

—^

⁺ T

^X j E ^{[ f (} t ) ^{f (} t ^- t s ) ^f ' ⁽ t ^{)] dt},

T

где

⁺ T

B(т) = Jim    [ B(tt - т)dt, т ^^ T

T 2

B T 3 ⁽ t s ) = ^ J^im T ^x K 3 т ^^ T

⁺ T

X j E [f (t) f (t - ts) f'(t - ts)] dt,

^— T

B ( 1 1 ,t 2 ) = Ef ⁽ m ⁾( 1 1 ) f ⁽ m ⁾( 1 2)) •

BT4(ts) = K4 Tm T X

Определив таким образом корреляционную функцию B ( t ), мы несколько расширили класс рассматриваемых процессов. Если в выражении (4) пренебречь вторым слагаемым, то воспользовавшись выражением (7), найдём спектральную плотность средней мощности процесса т ( t _s ):

⁺ T

X J E [ f (t) f (t - ts) f'(t) f'(t - ts)] dt

^— "T

Ф/( ш )

^Ф t ( ^ш ) = -tt •

s

Выражение (9) даёт приближение первого порядка, составляющие фазового шума соответствуют той же области частот, что и у аддитивного шума на входе. Для нахождения других спектральных составляющих постараемся учесть второе слагаемое. Подставив выражение (4) в (8), получим

Первому слагаемому при подстановке в (6) с учётом стационарности в широком смысле процесса f ( t ) соответствует результат (9). Если предположить, что производная процесса слабо коррелирована с его значением в этой точке, то усреднение от произведения равно произведению средних значений. Но так как среднее от производной равно нулю, то второе и третье слагаемые также равны нулю. Таким образом, четвертое слагаемое можно записать в виде

^х (1

BT (11 ,t 2)=Eff х

Ks2

^{T +} 2 11

B T 4 ⁽ t s ) =       l^{im         E [ f (} t ) ^{f (} t ^- t s ^{)] X}

K 4 т ^^ T

T 2

^^^^^^^^^r

f ' ( t 1 )      f ' ( t 2 )

^^^^^^^^^r

K s K s

+ f )],

Подставим получившееся выражение в (7) и представим результат в виде

b t ⁽ t s ) = b t 1 ⁽ t s ) + b t 2 ⁽ t s ^{) +}

+ B T 3 ⁽ t s ) + B T 4 ⁽ t s ) ,

где

T

⁺ 2

B T 1 ⁽ t s ) =     j™ ^E [ ^{f (} t ) ^{f (} t ^- t s ^{)] dt},

K sт -^ T

T 2

B T 2 ⁽ t s ) = ^ lim - ^х K s т -^ T

xE [f'(t) f'(t - ts)] dt

Поскольку процесс f ( t ) является стационарным в широком смысле, то входящие в интеграл выражения не зависят от переменной интегрирования t , и можно записать:

BT4(ts) = K4 Bf (ts)Bf' (ts), где

B f ( t s )= E [ f ( t ) f ( t - t s )] ,

Bf, (ts )= E [f' (t) f' (t - ts)] •

Выразим корреляционную функцию производной B f 1 ( t _s ) через корреляционную функцию самого процесса f ( t ) — B f ( t _s ).

Поскольку из сходимости в среднеквадратическом следует сходимость по вероятности, то

E ( f ' ( 1 1 ) f ' ( 1 2 )) =

= Bm E\f < t i + T > - f < t-I x t^ о         T f ( t 2 + T ) — f ( t 2)

x T . ’ учтя выражение (8), запишем:

E ( f ' ( 1 1 ) f ' ( 1 2 )) =

— lim — ⁽ B ⁽ t - + Tt 2 + T ) ^— t ^ 0 T

-

B ( 1 1 + T,t 2 )

-

^—B ^{( 1} 1 ^,1 2 + ^T ) + B ^{( 1} 1 ^,1 2 )) ^—

r 1

— lim — t^ 0 T 2

( B ( 1 1 ,1 2 )

+ £ t +

∂t ₁

-

+

∂B

∂t 2

_  1 d ² B

T +2 d1 1

1 d ² B

⁺ 2 d1 2

T ²

^^^^^^^^^r

1 d ² B

T ² +

∂2B

∂t 1 ∂t 2

B ( 1 1 ,1 2 )

^^^^^^^^^r

■ T ²+

∂B

— t — ∂t 1

-

2 d12

1 d ² B

2 d1 2

T ²

-

B ( 1 1 ,1 2 )

-

∂BT ∂t2

-

■ T ² +

B ^{( 1} 1 ^,1 2 ) + o ^{( T 2 )}^ ^—

∂2B

∂t1 ∂t2 .

Поскольку для стационарного в широ-

ком смысле процесса

B ^{( 1} 1 ^,1 2 ) ^— B ( ¹ s ) ,   ¹ s ^{— 1} 1 ^{— 1} 2 ,

то

∂2B    ∂   ∂B ∂ts

∂t ₁ ∂t ₂     ∂t ₂ ∂t _s ∂t ₁

∂2B ∂ts ∂ts   ∂B ∂2ts

∂ts2 ∂t2 ∂t1    ∂ts ∂t1 ∂t2

∂2B

∂ts2 .

Таким образом, получим корреляционную функцию процесса т ( 1 _s ):

R(+>₌ .кп(П-— ^{д 2} Bf ^{( 1}s ) ГШ

^{T (} s ) Ks2 Bf ⁽ s ) KS d12 ^{. ()}

Подставив её в выражение (6) и приняв во внимание, что оператор дифференцирования во временной области соответствует умножению на jω , а умножение — свёртке в частотной области, получим

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 Это и есть искомое выражение, учитывающее спектральные составляющие второго порядка.

Область применения оценки. При переходе от выражения (10) к (11) мы воспользовались предположением, что процессы f ( 1 ) и f ' ( 1 ) слабо связаны друг с другом, в результате чего сократилось 2-е и 3-е слагаемые в выражении (10), а четвертое представилось в виде произведения двух усреднений. Вообще говоря, это довольно жёсткое требование, в частности, не выполнимое для детерминированных сигналов. Однако если принять во внимание предел интегрального соотношения в выражениях B _{T 2} ( 1 s ), B _T з ( 1 s ) и B _{T 4} ( 1 s ), то мы придем к тем же результатам упрощения общего выражения для более широкого класса процессов.

Рассмотрим случай детерминированного гармонического воздействия: f ( 1 ) — sin( 1 ). Тогда произведению f ( 1 ) f ( 1 — 1 _s ) f ' ( 1 ) будет соответствовать сумма гармонических составляющих с фазами: 1 — 1 _s , 3 1 — 1 _s , 1 + 1 _s , интеграл по 1 будет конечным, а предел, входящий в состав выражения B _{T 2} ( 1 s ), будет равен нулю. То же самое относится и к B _{T 3} ( 1 s ). Результат 4-го слагаемого в выражении (10), очевидно, корректен, поскольку средним от детерминированной функции является само значение функции. Таким образом, выражение (12) вполне применимо и для детерминированного гармонического воздействия. Единственным существенным ограничением остаётся слабая версия условия 5 (со знаком «больше»): скорость нарастания фронта должна быть больше максимальной производной наведённой синусоиды.

Анализ фазового сдвига при гармоническом воздействии. Поскольку при отладке и тестировании наиболее распространенными являются синусоидальные воздействия, то рассмотрим их более подробно.

Спектральная плотность мощности синусоиды с частотой ω f равна

Ф т(^) — 772 ф f(ш) +

K _s

^ф f ^{( U} ) ^— 4 ^{( 5 ( U} f ^{— U} ) + ^{5 ( U} f + ^U )) .

+ ^

+ K4 J Ш2Фf(Us)фf(ш - Us)dUs.

— ^

Подставив это выражение в (12), получим

1                 U _f ²

фт(U) — 4K25(Uf ± U) + 16K45(2Uf ± U).

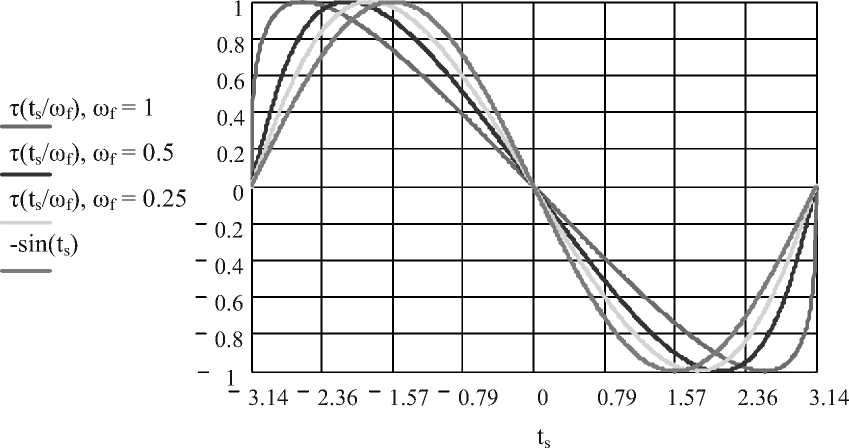
Рис. 4. Приведённые решения уравнения для гармонического воздействия разной частоты

На рис. 4 отображены приведённые графики численного решения уравнения (3) для воздействия:

f ( t ) = sin( u f • t ) ,K s = 1 ,U f = 1; 0 , 5; 0 , 25 , а также уравнение — sin( t ), являющееся ас-СИМПТОТОЙ при U f ^ 0.

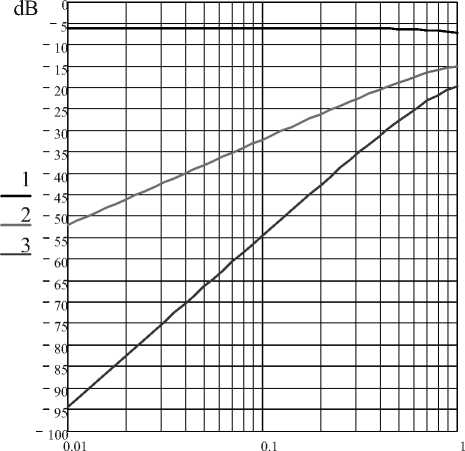
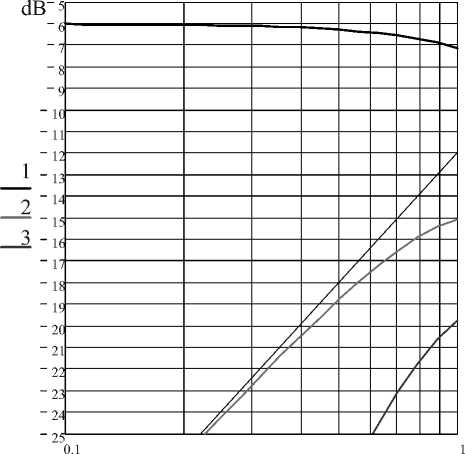
Как видно из графика, при увеличении частоты и приближении к границе условия 5 сильнее сказывается нелинейность уравнения (3). На рис. 5 представлена зависимость уровня первой, второй и третьей гармоник решения т ( t s ) от частоты гармонического входного воздействия ω f .

to f

Рис. 5. Уровень 1-й, 2-й и 3-й гармоники от частоты

Следует отметить, что уровень первой гармоники с ростом частоты практически остаётся без изменений, а уровень второй гармоники растёт со скоростью 20 dB/dec, что находится в согласии с полученным результатом (12).

На рис. 6 показана крупным планом область нелинейности и соответствующая ошибка оценки.

to f

Рис. 6. Ошибка оценки в нелинейной области

Таким образом, даже при достижении граничного условия по частоте величина ошибки первой гармоники составляет около 1 dB, а второй гармоники — не более 3dB.

• III.2. Фазовый шум как дискретный во времени процесс

В предыдущем разделе мы рассмотрели фазовый шум как непрерывный во времени процесс, образуемый за счёт непрерывного сдвига фронта опорного сигнала по оси времени. Теперь зададимся вопросом, как изменятся спектральные характеристики процесса, если фронт опорного сигнала появляется последовательно через равные промежутки времени, что и имеет место в реальном устройстве.

Пусть период опорного сигнала равен T . Представим сдвиги в моменты времени kT , k E N в виде дельта-импульсов с амплитудой т ( kT ). Выразим спектр данной реализации через спектр т ( t s ):

+ОО тт(ju) = 52 т(kT)e   ' = к =—га

+ га

= Е к=— га

+ га

• 2 - [ т ( ju 1 ) e j" ^{1 kT} du 1

• 2    п

  -∞

X

xe"^.

Воспользовавшись соотношением

+ “            ⁺ “

Е e—MT = T Е 5(u - ^k).

• к = — га               к = —га

получим т1 /т(ju )

1 ЕЕ (₍ 2 п Л T >, ^ти ^{( u} - Tk )) .

к = х то есть результирующий спектр равен сумме последовательно сдвинутого исходного спектра. Следует обратить внимание, что амплитуда т1 /т (ju) обратно пропорциональна периоду T . Если спектры не перекрывают друг друга, то для спектральной плотности мощности можно записать:

Фт/T(u) =     Е Фт(u - "E7k).

T 2

к = —^

или в пересчёте на фазу ( ф = 2 п Тт ):

Ф ф (ш) = 4 п 2Ф т/т (u).(14)

• III.3.    О спектральной плотности мощности периодического сигнала с фазовым шумом

Выражение (14) при малых ϕ соответствует величине соотношения первой гармоники сигнала на выходе компаратора к спектральной плотности шума при малой отстройке частоты. Эта величина выражается в едниницах dBc/Hz (децибел относительно несущей на герц) для заданной отстройки и является основной характеристикой качества сигнала гетеродина. Ее легко измерить при помощи анализатора спектра с достаточно узкополосным радиофильтром (RBW). То есть у периодического сигнала, подверженного действию фазового шума, его спектральная плотность мощности вблизи основной гармоники в точности повторяет спектральную плотность средней мощности фазового шума Фф (u). Это легко показать на примере синусоидального сигнала s (t) = sin(ust) и малого фазового сдвига ф (t). Результат воздействия фазового шума в таком случае будет s^ (t) = sin( ust + ф (t)) =

= cos(ust) sin(ф(t)) + sin(ust) cos(ф(t)). Разложив sin(ф(t)) и cos(ф(t)) ввиду малости ф(t) в ряд до первой степени, получим sv(t) = ф(t) cos(ust) + sin(ust).

Таким образом, спектральной плотностью мощности рассматриваемого сигнала, подверженного действию фазового шума, является дельта-функция, соответствующая исходному опорному сигналу s ( t ), и смещённая на ω _s спектральная плотность средней мощности процесса ф ( t ). Этот факт даёт возможность экспериментально определять спектральные характеристики фазового шума с достаточно высокой точностью.

• III.4.    Влияние цифрового делителя частоты

Для дальнейшего рассмотрения процесса преобразования фазового шума следует отметить, что подавляющее большинство фазовых детекторов, входящих в состав микросхем PLL (Phase Lock Loop), работают по одному из фронтов сигнала, для определённости, например, переднему. Поэтому значение сдвига важно лишь для

ТРУДЫ МФТИ. — 2009. — Том 1, № 2 этого фронта, положение другого практически никакого влияния не оказывает.

Рассмотрим теперь целочисленный делитель. По сути, он представляет собой счётчик по модулю N ,где N и есть коэффициент деления. Переключение счётчика также происходит по одному из фронтов сигнала, подаваемого на вход синхронизации. Таким образом, фазовый сдвиг на том фронте, по которому происходит переключение, без изменений транслируется на выход делителя (рис. 7) плюс к нему добавляется постоянное значение задержки. Очевидно, что эта постоянная составляющая дополнительного шума не вносит, поэтому её можно не учитывать.

Приняв во внимание выводы, сделанные в предыдущих разделах, выпишем результирующее выражение для расчёта фазового шума на выходе цифрового делителя при аддитивном воздействии на опорный сигнал, подаваемый на его вход:

• 4 п ² + ^         2 п

ФV (U) = NT2 L Фт (U ~ TTN k) , (15) к =—^