Влияние адгезионной добавки и природы наполнителя на межфазное взаимодействие и усталостные параметры асфальтовых вяжущих

Горбатова В.Н., Гордеева И.В., Дударева Т.В., Красоткина И.А. Влияние адгезионной добавки и природы наполнителя на межфазное взаимодействие и усталостные параметры асфальтовых вяжущих // Нанотехнологии в строительстве. 2024. Т. 16, № 5. С. 415–430. – EDN: KQNYDX.

Межфазное взаимодействие между битумом и каменными материалами асфальтобетонной смеси (щебень разных фракций, песок и тонкодисперсный наполнитель) во многом определяет эксплуатационные характеристики и срок службы всего дорожного покрытия. При приготовлении ас- фальтобетонной смеси сразу же за процессом смачивания поверхности каменных материалов происходит избирательная адсорбция компонентов битума. Активность адсорбции определяется природой, дисперсностью и удельной поверхностью каменных материалов, химическим составом битума и широко применяемых для улучшения адгезии поверхностно-активных веществ, а состав адсобрированного

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ битума характеризуется повышенной, по сравнению с объемным битумом, концентрацией наиболее высокомолекулярных и полярных компонентов [1].

На протяжении многих десятилетий внимание исследователей направлено на разработку эффективных методов оценки адгезии битума с каменными материалами [2]. В последние годы активно исследуется взаимосвязь межфазного взаимодействия и реологических свойств асфальтовых вяжущих, состоящих из матричной фазы битума и тонкодисперсного наполнителя [3-6].

Используя модель эмульсии Palierne [7], которая была разработана для системы твердых частиц, диспергированных в вязкоупругой подложке, физико-химическое взаимодействие между битумом и наполнителем может быть описано параметром межфазного взаимодействия K–B–G*через комплексные модули составляющих компонентов:

K-B-G*

(Gc / Gm) 1

(l.S+Gc’/G^X^ ,

где φ – объемная доля наполнителя; G*_c и G*_m – значения комплексного модуля для асфальтового вяжущего и матрицы (битумного вяжущего) в зависимости от частоты.

Одним из основных видов разрушений дорожных покрытий является образование усталостных трещин при так называемых средних температурах эксплуатации. Содержание асфальтового вяжущего в асфальтобетонной смеси составляет всего около 10–15%, однако при циклических нагрузках именно этот компонент может разрушаться в первую очередь и оказывать непосредственное влияние на усталостную долговечность покрытия.

Для оценки усталостных свойств битумных и асфальтовых вяжущих широко используется тест линейной амплитудной развертки (LAS) [8–9], выполняемый на реометре динамического сдвига. На первом этапе проведения испытаний по результатам частотной развертки в области LVE диапазона определяются вязкоупругие характеристики образца. На втором этапе, когда образец подвергается серии циклов колебательной нагрузки при увеличивающейся амплитуде деформации, определяются накопленные повреждения, что позволяет определить усталостные характеристики, приближенные к реальным условиям деформации битумного или асфальтового вяжущего в процессе эксплуатации дорожных покрытий [10].

Анализ усталостных свойств производят в соответствии c теорией VECD (система моделирования повреждений вязкоупругой сплошной среды – viscoelastic continuum damage), основанной на теории потенциала Schapery [11], где интенсивность накопления повреждений (D) зависит от потенциальной энергии (W), которая связана с ростом повреждений и параметра α, который определяется способностью данного материала накапливать повреждения:

dD/dt =-(div/dof .                  (2)

Основным элементом этой теории является построение зависимости, связывающей интенсивность накопления повреждений с функцией, характеризующей целостность материала при циклическом нагружении. Интенсивность накопления повреждений при определенном уровне разрушения, определяемом выбранным критериям разрушения, входит в определение коэффициента А в законе усталости для определения параметра усталостной долговечности N_f :

,                               13»

где N_f – число циклов до разрушения, В = 2α – характеризует неразрушенное состояние материала, определяют на основе экспериментальных данных LAS теста в первой его части при минимальной деформации. а γ _max – максимальная деформация при данной конструкции дорожного покрытия, которая принимается обычно как 2.5, 5 или 15% [12].

Расчет интенсивности накопления повреждений проводят по различным моделям теории VECD, основанным на энергии, которая определяет накопление повреждений [13–16]. В последнем стандарте AAS-HTO T391-20 [12], принятом в США, используется модель, основанная на рассеянной энергии деформации, где в качестве функции, характеризующей целостность материала, применяют модуль потерь:

,                               (4)

а накопление повреждений от времени испытаний определяется по формуле (5):

o(t) = Z^J^Dr^C^sm^i -

,               (5)

где I_D – значение комплексного модуля G* при деформации 1 %; γ _i, G_i , δ _i и t_i– текущие значения деформации, комплексного модуля, фазового угла и времени в испытании линейной амплитудной развертки (вторая часть LAS теста).

Вторая, широко используемая модель расчета основана на энергии псевдодеформации, а в качестве функции целостности материала при циклических нагрузках используется псевдожесткость [17–18]:

^- = -c_Y? ,                            (6)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ где γR – псевдо деформация, С – целостность материала, определяемая как псевдожесткость по формуле (7):

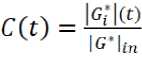
где | G*|_in и | G*_i|(t) – начальное (определяемое во второй точке) и текущее значения комплексного модуля, полученные во второй части LAS теста.

Интенсивность накопления повреждений в этом случае:

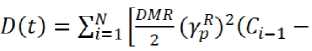
,                             (8)

?^ = ?<. ■ К^; 1лт ,                                (9),

С =

тр

,

где γ _p ^R – псевдодеформация при τ _p , α – параметр, характеризующий ненарушенное состояние образца (первая часть LAS теста), γ _p – деформация, определенная при τ _p на кривой τ(γ) в каждом цикле нагрузки, а DMR определяется как:

DMR = -—^ , l^G \lve

где | G*|_LVE – значение комплексного модуля, определенное в испытании частотной развертки (первой части LAS теста).

Для определения параметра B используют угол наклона зависимости логарифма модуля релаксации от времени ( m) . Из-за трудностей, связанных с проведением релаксационного испытания, модуль

релаксации обычно получают с помощью методов преобразования или, упрощая, строят зависимости комплексного модуля или модуля упругости ( G′ ) от частоты. Отметим, что зависимость B от угла наклона m остается открытой. Для асфальтобетонных смесей обычно принимают В = 2α, где α = 1/ m , тогда как для вяжущих применяется и эта формула, и формула α = 1/(1+ m ) [12, 19].

В данной работе поставлена цель - исследовать влияние адгезионной добавки и природы минерального наполнителя на межфазное взаимодействие в асфальтовых вяжущих на основе дорожного битума БНД 100/130 и оценить влияние толщины адсорбированного слоя битума на параметры усталостной долговечности асфальтовых вяжущих.

МАТЕРИАЛЫ И МЕТОДЫ

Материалы

В работе были использованы:

• •    Битум нефтяной дорожный марки БНД 100/130 по ГОСТ 33133 [20]: глубина проникания иглы (пе-нетрация) при 25°С – 115 × 0,1 мм; температура размягчения по кольцу и шару – 46°С; температура хрупкости по Фраасу – минус 23°С. Групповой химический состав битума, определенный по методу жидкостно-адсорбционной хроматографии с градиентным вытеснением [21], представлен на рис. 1.

• •    Наполнители:

  – минеральный порошок карбонатных пород марки МП-1 по ГОСТ Р 52129-2003 [22] (Н1);

  – порошок, полученный механическим дроблением некарбонатных пород (габбро) (Н2).

Распределение частиц наполнителей по размерам исследовали методом лазерной дифракции частиц в жидком потоке. Измерения выполняли на приборе ANALYSETTE 22 NanoTec plus с использованием

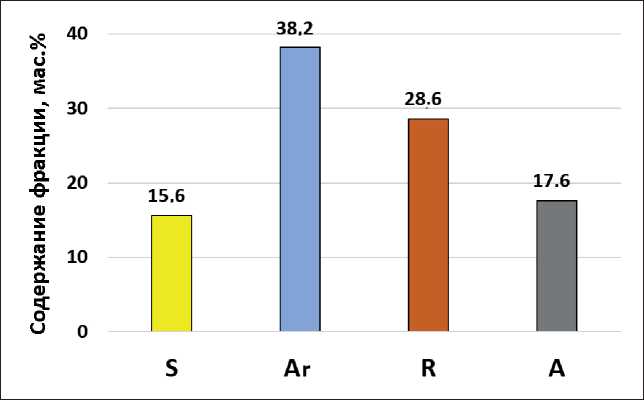
Рис. 1. Групповой химический состав битума: парафино-нафтеновые углеводороды (S), ароматические углеводороды (Ar), смолы (R), асфальтены (A)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ программного обеспечения FRITSCH MaS control. Полученные результаты представлены на рис. 2 и в табл. 1.

Удельную поверхность наполнителей определяли на приборе NOVA Series 1200e Quantachrome (USA) методом низкотемпературной адсорбции азота. Величину удельной поверхности и объем пор исследуемых образцов получали из анализа изотерм адсорбции-десорбции N2 при –196°С (77К), измеренных в области равновесных относительных давлений паров (Р/Р0) от 10–3 до 0,995. Образцы предварительно дегазировали при 180°С в течение 3 часов. Истинная плотность, удельная поверхность и значения параметров пористой структуры наполнителей, определенные по методу BET, представлены в табл. 1. Ошибка измерений не превышала 5–7%.

В соответствии с классификацией IUPAC [23] средний диаметр пор обоих наполнителей характерен для структуры с преобладанием мезопор. Полу- ченные результаты показали, что наполнитель Н2 отличается от наполнителя Н1 большим размером частиц, большей истинной плотностью и меньшими значениями удельной поверхности, объема и размера пор.

Адгезионная добавка

В качестве адгезионной добавки (АД) использовали поверхностно-активное вещество, применяемое в дорожном строительстве для улучшения сцепления нефтяного дорожного битума с каменными материалами как кислых, так и основных пород.

ИК спектр адгезионной добавки, полученный c использованием ИК-Фурье-спектрометра Thermo Scientific Nicolet iS50, приведен на рис. 3.

При изучении ИК-спектра адгезионной добавки отмечены хорошо выраженные пики 2952, 2922 и 2852 см–1, соответствующие –СН3, –СН2

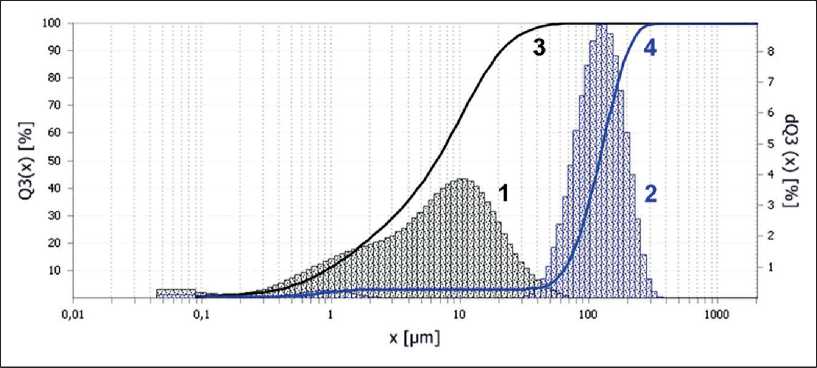
Рис. 2. Дифференциальная (1, 2) и интегральная (3, 4) кривые распределения частиц наполнителей по размерам: Н1 (1, 3), Н2 (2,4)

Таблица 1

Основные параметры наполнителей

Параметр		Наполнитель
		Н1	Н2
Распределение по размерам	D50, мкм	7	120
	D75, мкм	13	160
	D90, мкм	21	201
Истинная плотность, ρ, г/см3		2,71	3,05
Удельная поверхность, SBET, м2/г		4,214	1,437
Общий объем пор при относительном давлении Р/Р0 = 0,99, Vt, см3/г		0,0106	0,002742
Средний диаметр пор, Dпор, нм		10,1	7,63

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

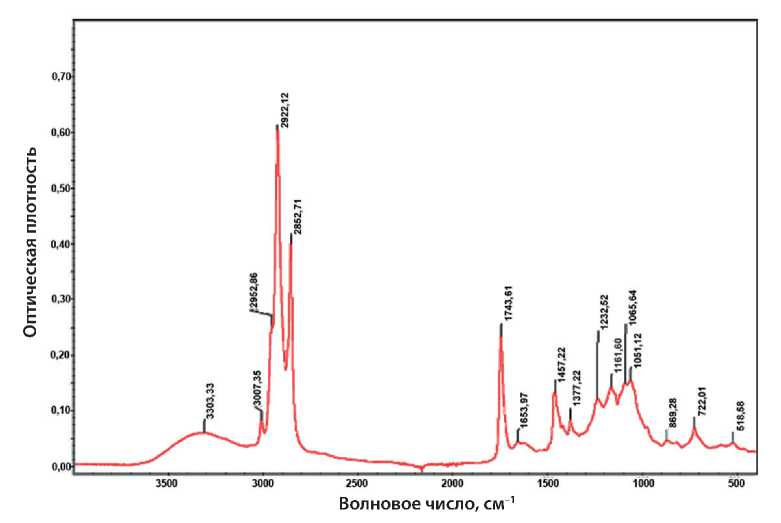
Рис. 3. ИК-спектр адгезионной добавки

и –СН-группам. Наличие более слабых по интенсивности пиков 1457 и 1377 см–1 свидетельствует о значительном содержании в адгезионной добавке предельных и ароматических углеводородов (парафинов, масел и т.д.). Полоса поглощения в области 3005–3007 см–1 образована валентными C–H колебаниями, проявляющимися у ненасыщенных жирных кислот. Широкая полоса поглощения при 3300 см–1 относится к валентным колебаниям О–Н связей фенола. Четко выражена полоса поглощения 1743 см–1, характеризующая карбонильные группы сложных эфиров насыщенных кислот. Полосы поглощения в области 1600–1560 см–1 характерны для функциональных групп С=О аминокислот. Пик при волновом числе 1065см–1 относится к валентным колебаниям С–N связей.

Приготовление образцов для проведения реологических испытаний

Известно, что термоистория образцов, размер пластин, толщина зазора между пластинами реометра и т.д. могут влиять на результаты измерений реологических свойств [24]. Поэтому все образцы для реологических испытаний готовили и испытывали в одинаковых условиях.

Образец Б представлял собой битум БНД 100/130, подвергнутый нагреву до 160°С и перемешиванию при этой температуре в течение 3 минут при скорости вращения мешалки 600 об/мин.

Образец Б-АД готовили аналогичным образом, добавляя адгезионную добавку в количестве 0,7 мас.% в битум перед его разогревом.

Асфальтовые вяжущие АВ1 и АВ2 получали смешением при 160°С предварительно нагретого до этой температуры битума БНД 100/130 (Б) и наполнителя (Н1 и Н2, соответственно) в течение 3 минут при скорости вращения мешалки 600 об/мин. Массу наполнителей подбирали с учетом истинной плотности так, чтобы объемная доля (Φ) наполнителей в АВ была одинаковой и составляла 0,275.

При приготовлении образцов асфальтовых вяжущих АВ1-АД и АВ2-АД, содержащих адгезионную добавку и наполнитель Н1 и Н2, соответственно, АД предварительно вводили в битум перед его разогревом в количестве 0,7 мас.%.

Для исключения процедуры повторного разогрева образцы сразу же после приготовления разливали в силиконовые формы диаметром 8 мм, выдерживали сутки при комнатной температуре и затем использовали для реологических испытаний.

Методы испытаний

Реологические испытания выполняли на реометре динамического сдвига «MCR 702e» («Anton Paar») с параллельной геометрией пластин диаметром 8 мм. Измерительный зазор составлял 2 мм. Образцы извлекали из силиконовых форм и укладывали между пластинами реометра, нагретыми до 64°С. Обрезку образцов производили при этой же температуре. Расхождение измеряемых параметров от среднего значения не превышало 3–7%.

Для оценки межфазного взаимодействия выполняли частотную развертку в диапазоне частот от 0,1 до 100 рад/с при деформации (γ) 0,05% при темпе-

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ ратурах от 30 до –10°С с шагом 10°С. Деформация 0,05% была выбрана, т.к. она находится в LVE диапазоне для всех образцов при –10°С (минимальное значение наблюдалось для AB и составляло 0,15%). Использовали один образец, который термостатировали после достижения заданной температуры испытаний в течение 10 минут.

Параметр К–В–G* , характеризующий физикохимическое взаимодействие между минеральным порошком и битумом, через комплексный модуль определяли по формуле (1). При определении отношения комплексных модулей асфальтового вяжущего к матрице ( G*_c /G*_m ) для АВ1 и АВ2 в качестве матрицы использовали данные для битума, а для АВ1-АД и АВ2-АД – для битума с адгезионной добавкой (Б-АД).

Толщину адсорбированного слоя ( d ) определяли по формуле (12):

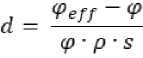
где φ _эфф = φ•( K–B–G* ) – эффективная объемная доля наполнителя, т.е. наполнитель вместе со слоем адсорбированного битума, φ – объемная доля наполнителя; ρ – плотность наполнителя, s – удельная поверхность наполнителя.

Усталостные испытания по методу линейной амплитудной развертки (LAS в соответствии с [12]) выполняли в диапазоне температур от 16 до 1°С с шагом 3°С. Верхнюю температуру диапазона испытаний выбирали так, чтобы начальное значение модуля потерь (G*sinδ) битума или битума с адгезионной добавкой превышало 5–6 МПа. Для каждой темпе- ратуры использовали новый образец. Первая часть испытаний выполнялась в режиме частотной развертки (ω = 0,2–30 Гц при деформации 0,1%). Далее, используя тот же образец, вторая часть испытаний выполнялась в режиме ступенчатой линейной амплитудной развертки при частоте 10 Гц в диапазоне деформаций 0.1%; 1% и далее с шагом 1% до 30% (по 100 циклов при каждом значении деформации, всего 3100 циклов).

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Межфазное взаимодействие и толщина адсорбированного слоя в асфальтовых вяжущих

На первом этапе работы методом частотной развертки было исследовано межфазное взаимодействие по параметру К–B–G * в асфальтовых вяжущих без адгезионной добавки (АВ1 и АВ2) и в ее присутствии (АВ1-АД, АВ2-АД). Особенностью испытаний было то, что один образец использовался для последовательных измерений при пяти температурах, начиная от 30°С и до –10°С с шагом 10°С и с термостатированием образца при каждой температуре.

Как можно видеть на рис. 4, при одинаковой объемной доле наполнителя (0,275) большее значение параметра K–B–G* как без адгезионной добавки, так и в ее присутствии наблюдалось для образца АВ1, т.е. при использовании в качестве наполнителя минерального порошка карбонатных пород Н1.

Параметр K–B–G* асфальтового вяжущего АВ2 на основе наполнителя порошка некарбонатных пород (габбро) Н2 оказался более чувствителен к веде-

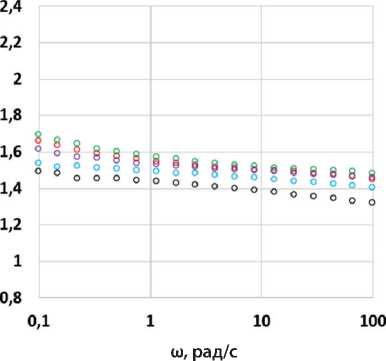
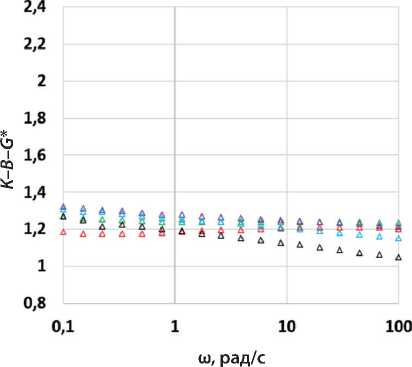
Рис. 4. Графики зависимости параметра межфазного взаимодействия K–B–G* от частоты испытаний (ω) для образцов: АВ1 (а), АВ2 (б), АВ1-АД (в), АВ2-АД (г) при температурах 30 (красный), 20 (зеленый), 10 (лиловый), 0 (голубой) и –10°С (черный)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

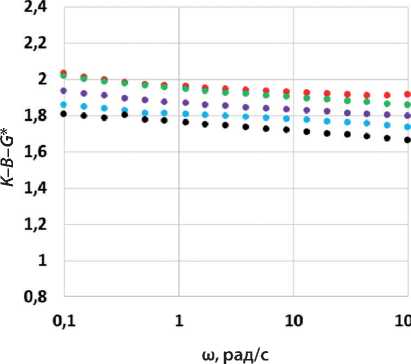
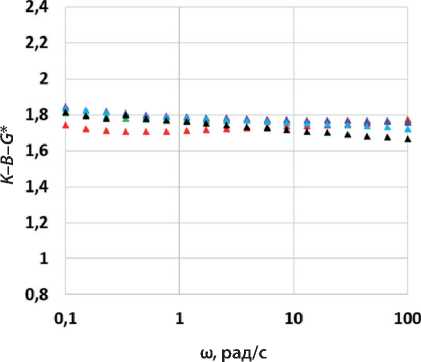
Рис. 4. Окончание нию адгезионной добавки. При этом чувствительность к воздействию температуры и частоты для образца АВ2-АД была меньше, чем для образца АВ1-АД.

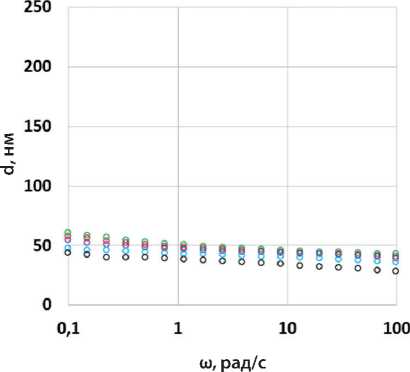
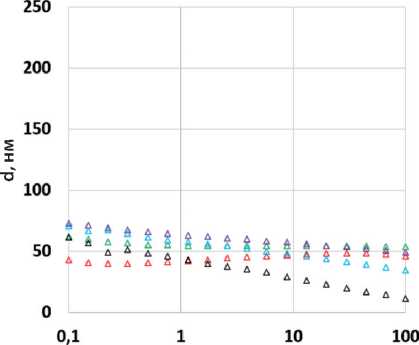
На рис. 5 для всех асфальтовых вяжущих представлены графики зависимости толщины адсорбированного слоя ( d ) от температуры и частоты испытаний. Толщина слоя в образцах, не содержащих адгезионную добавку, составляет от 60 до 30 нм для АВ1 и от 75 до 10 нм для АВ2 (см. рис. 5а и 5б).

Введение в асфальтовые вяжущие адгезионной добавки (АД) в обоих случаях увеличивает d (см. рис. 5 в и 5 г). Этот эффект проявлен в меньшей степени для образца АВ1-АД, в состав которого входит наполнитель Н1. При этом можно отметить тенденцию к увеличению зависимости толщины адсорбированного слоя от температуры по сравнению с образцом АВ1 без адгезионной добавки. Для АВ2-АД на основе Н2 можно отметить увеличение по сравнению с АВ2 толщины межфазного слоя более чем в 2 раза (до 190–150 нм).

Усталостные испытания

Область температур испытаний, где механизм разрушения определяется усталостными свойствами материла без влияния текучести и потери адге-

ω, рад/с

Рис. 5. Графики зависимости толщины адсорбированного слоя d от частоты испытаний (ω) для образцов: АВ1 (а), АВ2 (б), АВ1-АД (в), АВ2-АД (г) при температурах 30 (красный), 20 (зеленый), 10 (лиловый), 0 (голубой) и –10°С (черный)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

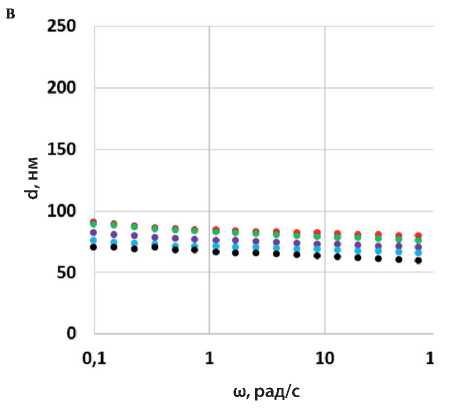
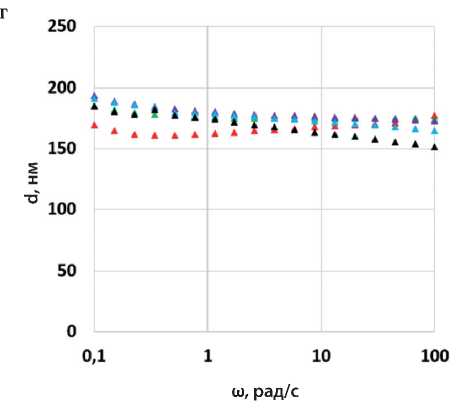
Рис. 5. Окончание зии, рекомендовано выбирать таким образом, чтобы комплексный модуль сдвига находился в диапазоне от 12 до 60 МПа [25]. В табл. 2 приведены зависимости параметров G* (ID) и G*sinδ (С0) от температуры испытаний. В соответствии с общепринятым подходом, ID определяли как начальное значение комплексного модуля G* при деформации 1 %; а С0 как среднее значение G*sinδ при деформации 0,1%.

Как можно видеть из табл. 2, для образца битума (Б) С0 при температуре 16°С составляет 6,6 МПа, что довольно близко к значениям, характеризующим не усталостное поведение, а пластическое течение в процессе испытаний. Из приведенных данных также можно видеть, что введение наполнителей в битум привело к увеличению ID и эквижесткие (или близкие к ним) образцы наблюдаются при испытаниях на 6 градусов выше. Введение адгезионной добавки в битум и АВ снизило значение ID образцов, и эквижесткие образцы наблюдаются во всех случаях при испытаниях на 3 градуса ниже.

Так, например, значения параметра I_D, близкие к 22 и 32 МПа, соответствуют температурам испыта-

Таблица 2

Зависимости параметров I_D и С₀ от температуры испытаний

Параметр		Образец
		Б	Б-АД	АВ1	АВ1-АД	АВ2	АВ2-АД
ID , МПа
Температура, °С	16	10,2		22,1		21,4
	13	14,5		33,8	24,8	35,8	19,6
	10	22,1	12,3	53	29,4	48	31
	7	31,7	20,2	61,8	50,6	59,5	43,5
	4	42,1	31,6		76,2		63,8
С0, МПа
Температура, °С	16	6,6		15,9		15,7
	13	9,0		22,9	16,3	24,7	13,5
	10	12,6	7,4	32,5	17,9	29,1	20,0
	7	16,8	11,0	35,5	30,9	36,6	26,0
	4	21,4	16,5		40,7		36,7

Примечание: тонировка ячеек выполнена для двух групп эквижестких (или близких к ним) образцов.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

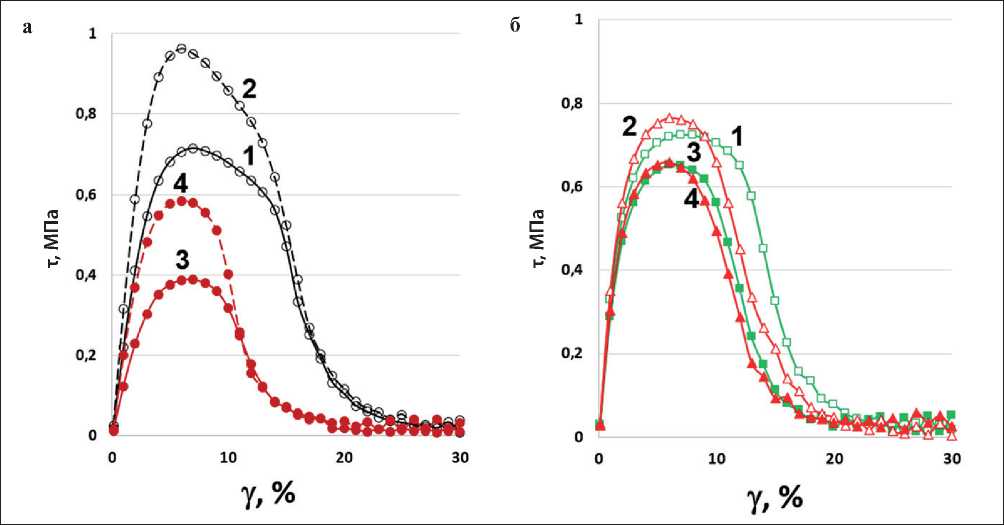
Рис. 6. Зависимость напряжения сдвига (τ) от деформации (γ) для образцов: а) битум (1, 2) и Б-АД (3,4) при температурах 10 (1, 3) и 7°С (2, 4); б) для АВ1 (1) и АВ2 (2) при 13°С и АВ1-АД (3) и АВ2-АД (4) при 10°С

ний 10 и 7°С для битума, 7 и 4°С для Б-АД, 16 и 13°С для АВ1 и АВ2, 13 и 10°С для АВ1-АД и АВ2-АД. Вместе с тем, как можно видеть на рис. 6, где приведены графики зависимости напряжения сдвига (τ) от деформации (γ), в процессе усталостных испытаний поведение эквижестких образцов с адгезионной добавкой и без нее существенно различается.

Так, на рис. 6а эквижестким образцам соответствуют кривые 1 (битум, при 10°С) и 4 (битум с адгезионной добавкой при 7°С). Снижение температуры испытаний для образцов Б и Б-АД приводит к увеличению максимального напряжения сдвига и уменьшению соответствующей ему деформации. При этом введение в битум адгезионной добавки снижает максимальное напряжение сдвига, что должно положительно сказываться на усталостной долговечности, но изменяет поведение постпикового участка кривой, что, по-видимому, может отражать более быстрое разрушение образца в процессе испытаний. Аналогичную тенденцию более резкого снижения τ после прохождения максимума можно проследить, сравнивая кривые τ(γ) эквижестких образцов АВ и АВ-АД (рис. 6б).

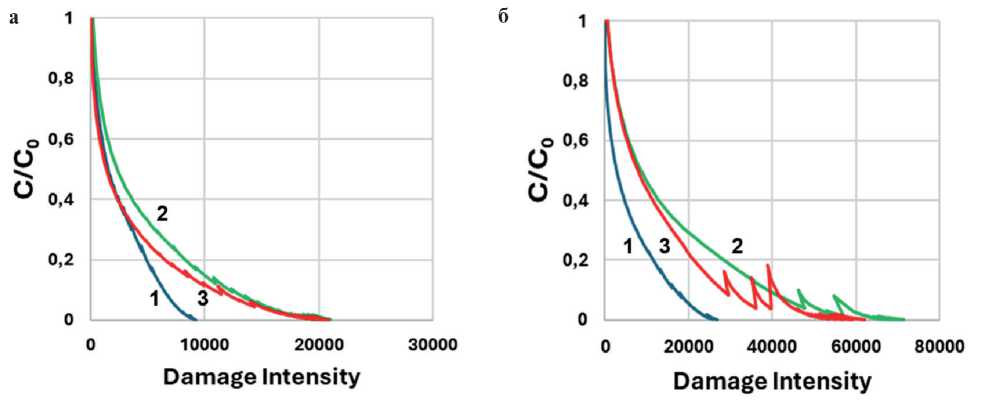
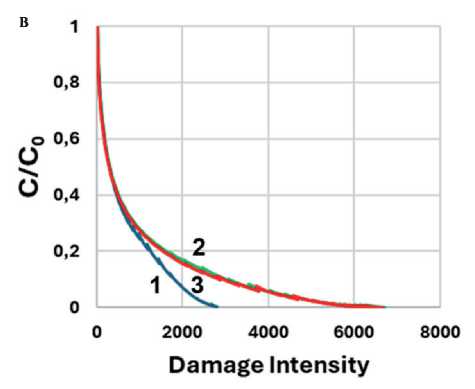
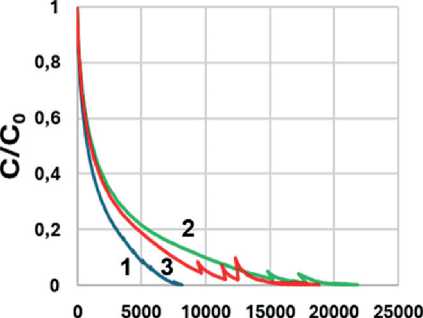
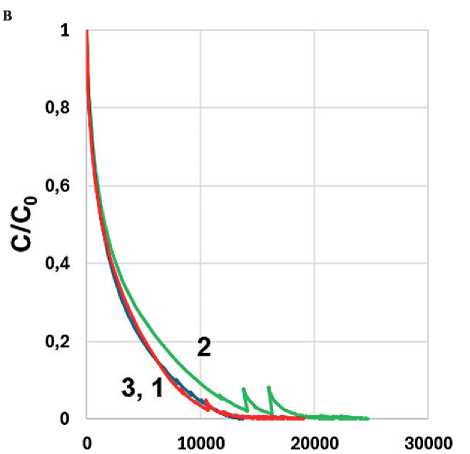
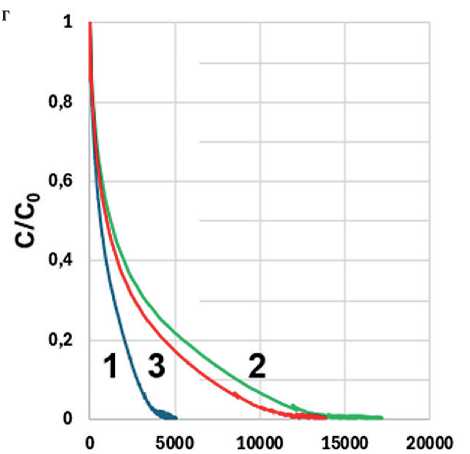
Для характеристики усталостной долговечности в теории VECD анализируется кривая зависимости накопления повреждений от деформации (Damage Curve), отражающая потерю структурной целостности материала при циклическом нагружении. На рис. 7 представлены Damage Curve, представляющие собой зависимость отношения параметра С (текущего мо- дуля потерь (G*•sinδ) в модели рассеянной энергии деформации (см. рис. 7а и 7б) и комплексного модуля (G*) в модели энергии псевдодеформации (см рис. 7в и 7г) к его начальному значению С0 от интенсивности накопления повреждения (Damage Intensity). Анализируя представленные данные, следует помнить, что значение С/C0 = 1 соответствует деформации γ = 0,1%, а минимальное значение С/C0 для каждой кривой фиксируется при γ = 30%. Появление зубцов, возможно, связано с особенностями расчета Damage Intensity по различным моделям и краевыми эффектами при больших деформациях сдвига.

Как можно видеть из рис. 7а и 7в, при температуре 16°С наименьшее накопление повреждений по обоим расчетным моделям проявляет битум, в то время как для образцов асфальтовых вяжущих при расчете по методу энергии псевдодеформации практически отсутствует разница между кривыми. При понижении температуры (см. рис. 7б, 7г и рис. 8), а также при введении адгезионной добавки (рис. 8) проявляется преимущество образца АВ2, что может быть связано с большей толщиной адсорбированного слоя.

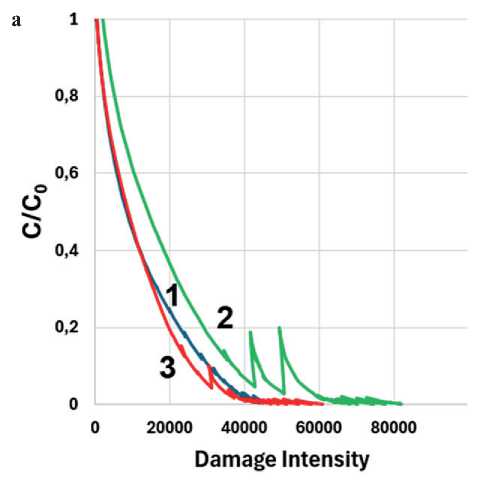
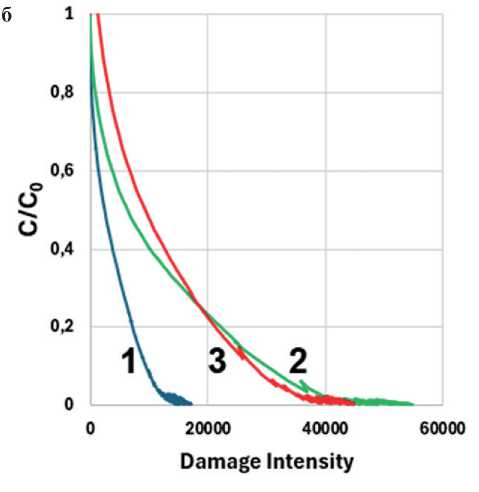
Следует обратить внимание на то, что при температуре 7°С ухудшается устойчивость к разрушению образца битума без адгезионной добавки (рис. 8а, в), так что кривая битума оказывается близка к кривой АВ2. Учитывая высокое (15,6%) содержание па-рафино-нафтеновых углеводородов в битуме (см. рис. 1), можно предположить протекание в этом

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Damage Intensity

Рис. 7. Зависимость С/C 0 от Damage Intensity: (а) при температуре 16°С (а, в) и 10°С (б, г) для образцов: Б (1) АВ1 (2), АВ2 (3) по моделям рассеянной энергии деформации (а, б) и энергии псевдодеформации (в, г)

температурном диапазоне процессов структурирования, связанных с кристаллизацией (плавлением) н-алканов (парафинов) [25]. Структурирование битума приводит к появлению новых границ раздела, по которым также может происходить зарождение микротрещин. Добавление адгезионной добавки, по-видимому, сдвигает структурирование битума в область более низких температур, и при температуре 7°С (рис. 8б и 8г) битум с адгезионной добавкой опять имеет преимущество перед асфальтовыми вяжущими с той же АД.

На рис. 9 представлены кривые зависимости интенсивности накопления повреждений от температуры. Расчет проводили по модели рассеянной энергии деформации и двух вариантов критерия отказа (разрушения, failure) – С/C0 = 0,65 [12] и С/C0 при τmax на кривой τ(γ) в тесте амплитудной развертки. Па- раметр α, входящий в расчет Damage Intensity, определяли двумя способами как α = 1+1/m и α =1/m.

Аналогичные кривые, полученные по модели энергии псевдодеформации для критерия отказа С/C ₀ при τmax на кривой τ(γ) и двух вариантах определения параметра α, представлены на рис. 10.

Для всех вариантов расчетов, критериев разрушения и вариантов определения параметра α можно отметить общие тенденции, заключающиеся в том, что при одной температуре ранжирование образцов в порядке убывания накопленных повреждений (Damage Intensity) выглядит следующим образом: АВ1, АВ2, АВ1-АД, АВ2-АД. Сопоставляя данные, приведенные на рис. 9–10 и рис. 5 и 7–8, можно проследить определенную корреляцию между толщиной адсорбированного слоя ( d ) и Damage Intensity: увеличение d приводит к снижению Damage Intensity.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Damage Intensity

Damage Intensity

Рис. 8. Зависимость С/C₀ от Damage Intensity: (а) при температуре 7°С для образцов без АД (а, в) и с АД (б, г): Б (1) АВ1 (2), АВ2 (3) по моделям I (а, б) и II (в, г)

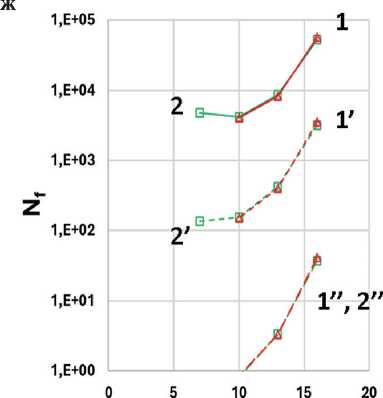
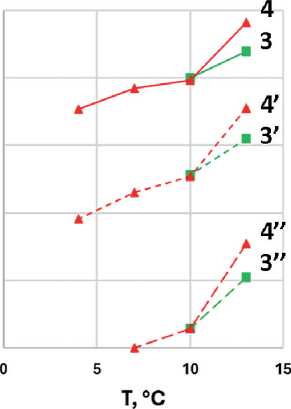
К сожалению, применение моделей расчета для параметра Nf не дало однозначного результата. На рис. 11 для образцов асфальтовых вяжущих представлена зависимость от температуры параметра числа циклов до разрушения (Nf) для деформаций 2,5, 5 и 15% при расчете по модели рассеянной энергии деформации при α = 1+1/m и α = 1/m и критерию разрушения (отказа, failure) при τmax на кривой τ(γ). Для всех образцов Nf уменьшается при понижении температуры. В отсутствии адгезионной добавки зна- чения Nf для образца АВ1 близки к битуму (кривая не приводится) и превышают значения Nf для образца АВ2. Добавление адгезионной добавки несколько снижает Nf битума (кривая не приводится) и АВ1, в то время как для АВ2 наблюдается увеличение усталостной долговечности независимо от того, по какой формуле производится расчет параметра α.

Графики зависимости N_f от температуры при расчете по модели энергии псевдодеформации для образцов без адгезионной добавки носят тот же ха-

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

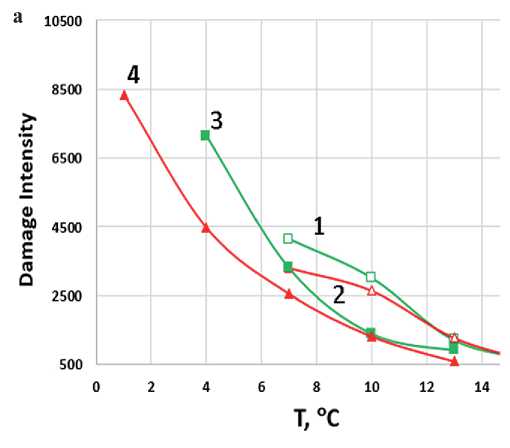
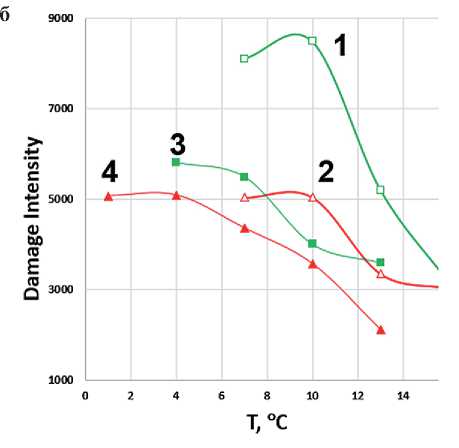
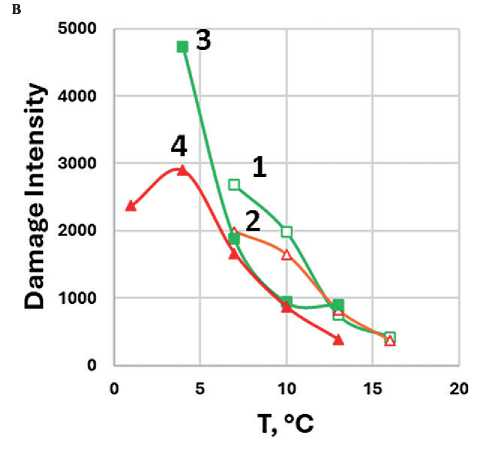
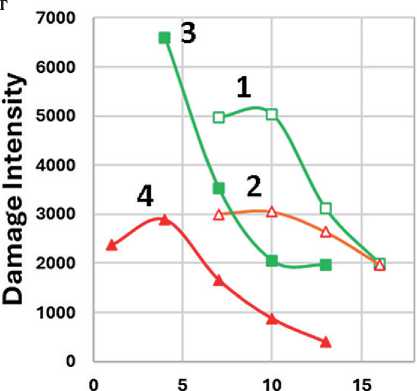
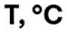
Рис. 9. Зависимость накопления разрушений (Damage Intensity) от температуры при расчете по модели рассеянной энергии деформации при α = 1+1/ m (а, б) и α = 1/ m (в, г) и при критериях разрушения: С/C ₀ = 0,65 (а, в), С/C ₀ при τmax на кривой τ(γ) (б, г) для образцов АВ1 (1), АВ2 (2), АВ1-АД (3), АВ2-АД (4)

рактер, но различия между образцами АВ1 и АВ2 практически отсутствует, независимо от способа расчета параметра α. Образец АВ2-АД демонстрирует несколько большую усталостную долговечность по сравнению с АД1. А вот кривая N_f ( T ) образца битума с адгезионной добавкой возрастает при понижении температуры (кривая не приводится), что вызывает сомнение в применимости данного метода расчета для прогнозирования усталостной долговечности в таких образцах.

Таким образом, удалось проследить только некоторые тенденции влияния толщины адсорбированного слоя в асфальтовых вяжущих и асфальтовых вяжущих, содержащих адгезионную добавку, на накопление повреждений (Damage Intensity), но не на параметр усталостной долговечности Nf.

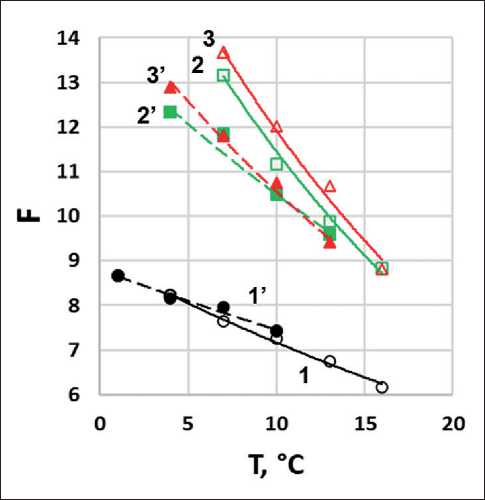
Интересную закономерность удалось проследить по параметру F , который фактически характеризует скорость нарастания энергии псевдодеформации. Ранее было показано, что более низкое значение параметра F связано с более высокой усталостной долговечностью образца [26]. Как можно видеть на рис. 12, введение наполнителя Н2 приводит к более сильному ухудшению усталостной долговечности битума по сравнению с Н1. Введение адгезионной добавки приводит к снижению величины F для ас-

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

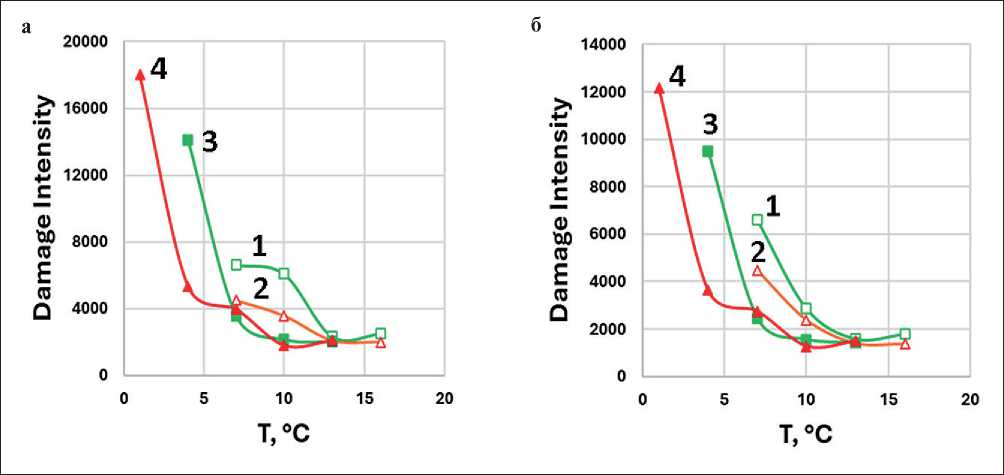
Рис. 10. Зависимость накопления разрушений (Damage Intensity) от температуры при расчете по модели энергии псевдодеформации при α = 1+1/ m (а) и α = 1/ m (б) и критерии разрушения (отказа) С/C ₀ при τ_max на кривой τ(γ) для образцов АВ1 (1), АВ2 (2), АВ1-АД (3), АВ2-АД (4)

фальтовых вяжущих, т.е. увеличивает их усталостную долговечность, причем это увеличение больше проявлено для АВ с наполнителем Н2, у которого толщина адсорбированного слоя выше. Следует отметить, что для битума влияние адгезионной добавки на этот параметр практически отсутствует.

ЗАКЛЮЧЕНИЕ

В работе были использованы стандартный минеральный порошок карбонатных пород (Н1) и наполнитель некарбонатных (габбро) пород (Н2), отличавшийся от Н1 большим размером частиц, боль-

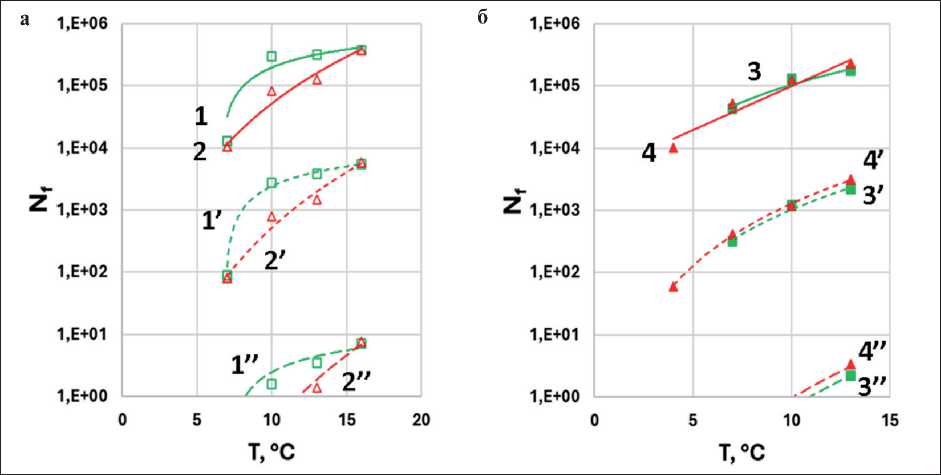
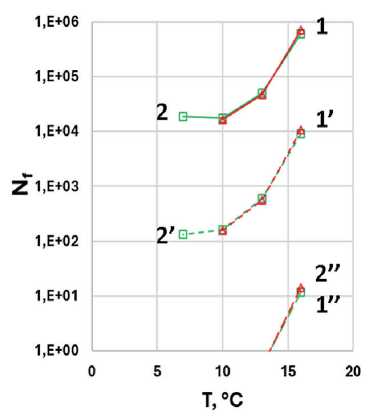
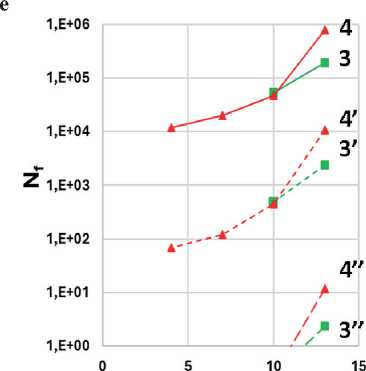
Рис. 11. Зависимость числа циклов до разрушения ( N_f ) при расчете по модели рассеянной энергии деформации при α = 1+1/ m (а, б) и α = 1/ m (в, г) и по модели энергии псевдодеформации при α = 1+1/ m (д, е) и α = 1/ m (ж, з) при критерии разрушения (отказа, failure) τ _max на кривой τ(γ) для образцов АВ1 (1), АВ2 (2); АВ1-АД (3), АВ2-АД (4) при деформациях 2,5% (1–4), 5% (1’–4’) и 15% (1’’–4’’)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

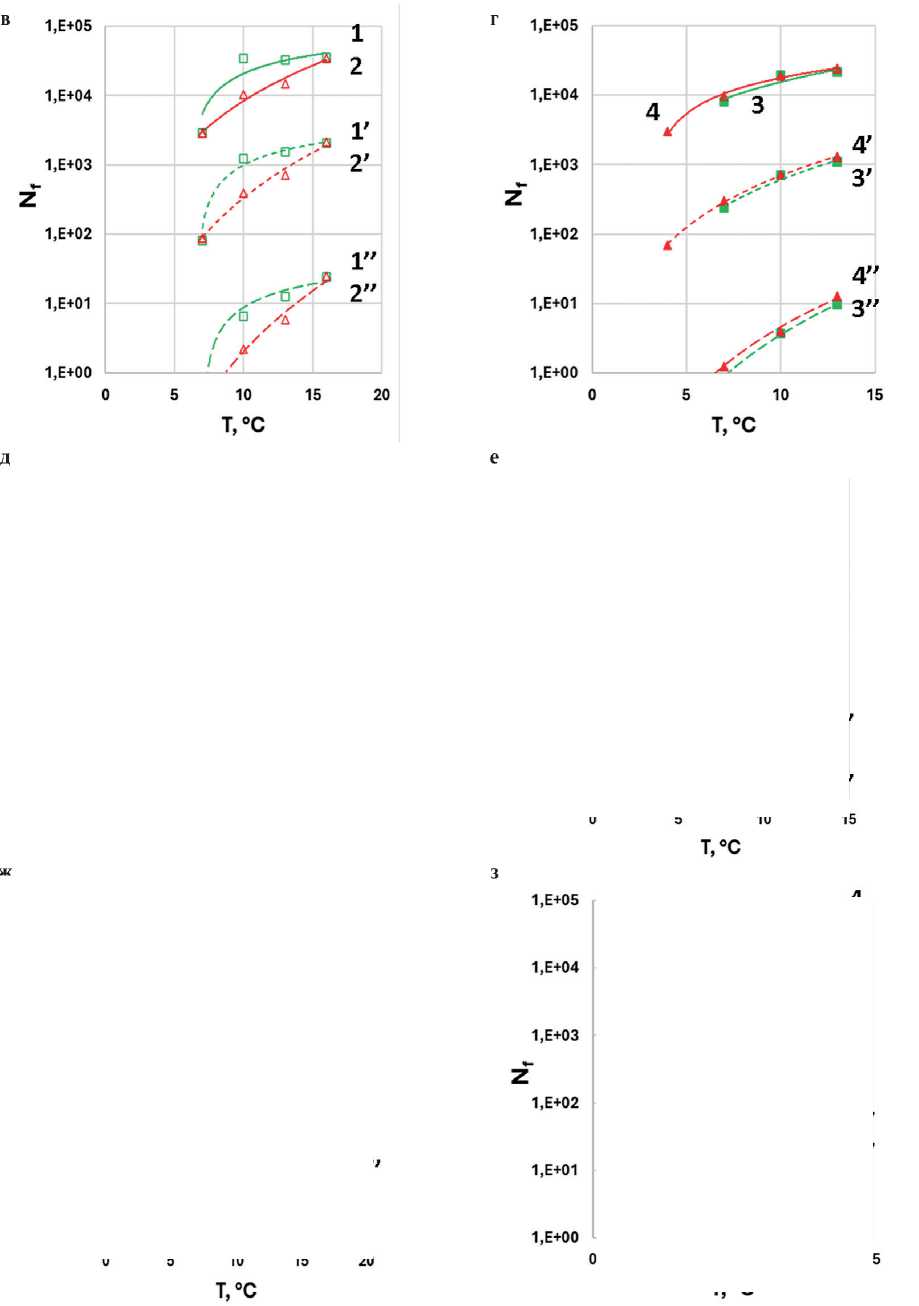
Рис. 11. Окончание

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

шей истинной плотностью и меньшими значениями удельной поверхности, объема и размера пор. При одинаковой объемной доле наполнителя (0.275) в асфальтовых вяжущих на основе битума БНД 100/130 большее значение параметра K–B–G* как без адгезионной добавки, так и в ее присутствии наблюдалось для образца асфальтового вяжущего (АВ) на основе наполнителя Н1. Введение адгезионной добавки в асфальтовое вяжущее на основе напол-

Рис. 12. Зависимость параметра F от температуры для образцов: битум (1), АВ1 (2), АВ2 (3); Б-АД (1’), АВ1-АД (2’), АВ2-АД (3’)

нителя Н2 привело к большему, по сравнению с АВ на основе Н1, росту параметра K–B–G* , снижению его чувствительности к воздействию температуры и частоты испытаний. Толщина адсорбированного слоя при применении адгезионной добавки (АД) существенно увеличивается в асфальтовом вяжущем с наполнителем H2.

Для оценки усталостной долговечности по результатам LAS теста были использованы различные модели VECD теории, критерии разрушения и варианты параметра неразрушенной структуры α. Для всех вариантов расчетов наблюдаются тенденции сохранения ранжирования образцов по устойчивости к накоплению повреждений (Damage Intensity) при одной температуре: AВ1 < AВ2 < AВ1-AД < AВ2-AД. Увеличение толщины межфазного слоя (d) приводит к снижению Damage Intensity. Однозначных данных по зависимости параметра усталостной долговечности – числа циклов до разрушения ( N_f ) от температуры – получить не удалось. Показано, что увеличение толщины адсорбционного (межфазного) слоя приводит к улучшению усталостной долговечности, определяемой по усталостному критерию F .

Работа будет продолжена с расширением круга исследуемых объектов: битумов, наполнителей и адгезионных добавок.