Влияние амплитуды деформации и всестороннего давления на скорость и затухание p- и s-волн в сухом и водонасыщенном песчанике: экспериментальное исследование

Введение и постановка проблемы

В современном развитии наук о Земле повышение геологической эффективности сейсмических и акустических методов опирается на новые фундаментальные знания в физике деформирования горных пород. О механизме деформации природных материалов при различных нагрузках получены новые знания. Это неупругие скачкообразные, прерывистые деформации, регистрируемые на микро/нано уровне. Малоизвестное в геофизике свойство микропластичности горных пород может проявляться при малых и даже очень малых деформациях. Учет этого фактора важен для практики, так как сейсмические и акустические методы используют диапазон малых деформаций. Интерес к этому эффекту проявился в результате предыдущих исследований. Изучение нелинейности в сейсмике привело к необходимости глубокого понимания физики деформирования пород [1–3]. Была подтверждена возможность нелинейности при очень малых деформациях, что расширило границы действия неупругих процессов [4, 5]. Теоретические исследования в сейсмике совершенствуют классическую вязкоупругую модель стандартного тела. Модель хорошо описывает дисперсию, релаксацию и связанные с нею неупругие процессы.

Теоретические и эксперименты исследования подтверждают наличие эффекта микропластичности [6, 7]. Влияние амплитуды деформации на скорость волны и затухание неоднозначно, так как приводит в одном случае к увеличению параметров, в другом – к уменьшению. Таким же образом изменяется модуль упругости, что влияет на кривизну соотношения «напряжение–деформация» [8, 9]. Такое нестандартное поведение пород обусловлено совместным действием упругой и микропластической деформации [10, 11].

На диаграмме «напряжение–деформация» и на записи акустического сигнала этот эффект представлен в виде «стресс-плато» и «стресс-падение» [12. 13]. Свойство микро-пластичности пород допускает нерегулярное кратковременное «включение» процесса пластичности с одновременным действием упругой деформации. Имеются также теоретические подтверждения [14–16]. Механические свойства горных пород в большей степени различаются по их неупругим характеристикам. Они больше связаны с динамическими параметрами волн, чем с упругими характеристиками. Современный подход предполагает использование новых данных, которые могут быть использованы для решения геологических задач. Это подтверждают высокоточные экспериментальные и теоретические исследования [17, 18].

Исследования в физике твердого тела показали, что вязкоупругая модель может быть дополнена неупругим элементом прерывистого характера, участвующим в процессе деформирования. Упруго-вязкопластическая модель с участием пластической составляющей способна представлять амплитудно-частотно-зависимый динамический модуль. В этой модели общий тензор напряжения определен суммой трех компонент – упругого, упругопластического и вязкоупругого модулей материала [19–21]. В физике твердого тела и материаловедении большое внимание уделяется исследованию скачкообразной деформации [22–24]. Имеет место резкий переход от упругого деформирования к пластическому течению. Такой скачок деформации сопровождается падением напряжения и сложным образом зависит от свойств материала и условий его нагружения [25, 26]. Развитие механической модели геологической среды базируется на учете данных, полученных о прерывистой неупругости. Некоторые https://mst.misis.ru/

2023;8(1):22–29

данные для горных пород (песчаник, суглинки, кварц, кремний, мусковит, стишовит, слюда, сапфир, диорит, графит) описаны в работах [27, 28].

В этой статье описывается лабораторное исследование влияния амплитуды деформации и давления на поведение скорости и затухания продольной и поперечной волны в сухом и водонасыщенном песчанике при комнатной температуре. Это исследование представляет большой интерес для понимания микро-деформационных механизмов в горных породах. Механизм микропластичности горных пород пока мало изучен, но есть основания утверждать, что он близок к механизму, известному в физике твердого тела. Микропластическое поведение происходит при активизации подвижных дислокаций в виде лавинного явления. Первым признаком этого процесса является появление эффекта «стресс-плато» и «стресс-падение». Результаты, полученные в этом эксперименте, могут быть полезны не только как фундаментальные знания, но также для их применения в решении практических задач. Новые знания о свойстве микро-пластичности горных пород позволяют усовершенствовать стандартную вязкоупругую модель, используемую в сейсмических исследованиях. Это может быть достигнуто включением в стандартную модель компоненту микропластической деформации. Комплексная вязко-упруго-пластическая модель может более реалистично описывать процессы деформации в горных породах. При практическом применении полученных знаний, например, в сейсмике и акустике необходимо учитывать амплитудно-зависимый эффект, который влияет на скорость и затухание продольных и поперечных волн в горных породах. Учет этого эффекта повышает точность измерения и интерпретацию полученных данных.

Методики исследования и фактический материал

В эксперименте были использованы образцы мелкозернистого песчаника из керна, взятого с глубины 2545 м. Плотность песчаника 2,45 г/см³, содержание мелкозернистой песчаной фракции 82 % и алевролита 18 %, общая пористость 12 %. Измерение скорости и затухания P- , S -волны в зависимости от величины амплитуды деформации проводилось при постоянном гидростатическом давлении 20 МПа. Кроме того, на постоянной амплитуде было изучено поведение скорости P- , S -волны в зависимости от величины гидростатического давления в диапазоне от 10 до 50 МПа. Образцы цилиндрической формы имеют размеры: 40 мм в диаметре и 16 мм в длину. Использовалась стандартная установка в виде трехслойной модели [29, 30]. Первый и третий слои (бериллиевая бронза) обеспечивают идентичное отражение волны на границах раздела. Первый слой – линия задержки, а третий слой – акустическая нагрузка. Образец породы располагается между этими слоями. Возбуждение и прием акустических сигналов обеспечивают пьезокерамические датчики на частоте 1 МГц, которые поляризованы на продольную и поперечную волны. Декремент затухания вычислялся как [11, 31, 32]:

-1 _ a V _ aX ~ = 8,686^7 " 8,686л, где α – коэффициент поглощения, дБ · м-1,

8,686 a(to) = — l — In

где L – двойная длина образца, м; A_top ( f ) – амплитуда Фурье отраженного импульса от верхней границы образца; A_bot ( f ) – амплитуда Фурье отраженного импульса от нижней границы образца; R ₁₂( f ) – коэффициент отражения от верхней границы; R ₂₃( f ) – коэффициент отражения от нижней границы. В нашем случае границы являются идентичными и поэтому R ₁₂( f ) = - R ₂₃( f ). Коэффициент отражения

R ( f ) =

P V ( f )-P b V b ( f ) P r V r ( f ) + P b V b ( f ),

где ρ _r и ρ _b – плотность породы и бериллиевой бронзы, кг · м^-3, соответственно; V_r ( f ) и V_b ( f ) – скорости волны, м · с^-1; V – фазовая скорость, м · с^-1; f – частота, Гц.

При измерении скорости волны и затухания изменение величины амплитуды деформации происходило по замкнутому циклу. Сначала амплитуда возрастала от минимальной до максимальной величины (восходящий курс), затем по тем же величинам уменьшалась (нисходящий курс). Полный курс: ε ₁ ≈ 0,5×10^-6 → ε ₂ ≈ 1,0 × 10^-6 → ε ₃ ≈ 1,3 × 10^-6 → ε ₄ ≈ 1,67 × 10^-6 → ε ₃ ≈ 1,3 × 10^-6 → ε ₂ ≈ 1,0 × 10^-6 → ε ₁ ≈ 0,5 × 10^-6. Увеличение и последующее уменьшение амплитуды на всех рисунках помечено стрелками. Регистрация импульсов проводилась с накоплением сигналов. Это обеспечивает повышенную помехоустойчивость.

Результаты исследований

На рис. 1 и 2 представлена зависимость скорости P - и S -волны от амплитуды деформации в сухом и водонасыщенном (50 %) песчанике на постоянном давлении 20 МПа. На рис. 1 в сухом песчанике на восходящем и нисходящем курсе амплитуды деформации скорость P -волны возрастает на 1,12 %. В водонасыщенном песчанике изменение скорости волны при тех же условиях составляет 0,28 %. Диаграммы скоростей представляют незамкнутые петли гистерезиса (помечены скобками). Открытый гистерезис сухого и насыщенного песчаника составляет соответственно 1,41 и 0,28 %. Изменение скорости S -волны при тех же условиях измерения не превышало 0,35 %. Незамкнутая часть петли гистерезиса для сухого и смоченного песчаника составляет 0,54 и 0,35 % соответственно.

На рис. 3 представлено затухание P-волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике при постоянном давлении. В сухом песчанике при изменении амплитуды от минимальной до максимальной величины затухание волны нелинейно возрастает на 5,43 %. При возвращении амплитуды к минимальной величине затухание уменьшается до начальной величины. В результате петля гистерезиса затухания является замкнутой. В смоченном песчанике увеличение амплитуды слабо https://mst.misis.ru/

2023;8(1):22–29

влияет на затухание. На обратном курсе амплитуды затухание уменьшается на 4,93 %, что приводит к появлению незамкнутой петли гистерезиса. График смоченного песчаника располагается выше графика сухого песчаника.

На рис. 4 показано затухание S -волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике при постоянном давлении. Графики сухого и смоченного песчаника существенно удалены друг от друга. Величина затухания волны в сухом песчанике значительно меньше, чем в смоченном. В обоих случаях с увеличением амплитуды затухание уменьшается. В сухом и смоченном песчанике уменьшение затухания составляет 8,81 и 2,71 % соответственно. Обе петли гистерезиса незамкнутые. Величина открытой петли гистерезиса в обоих случаях не превышает 0,8 %.

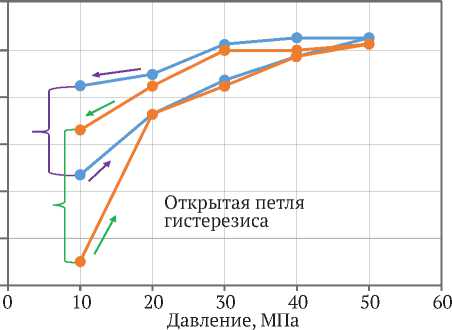
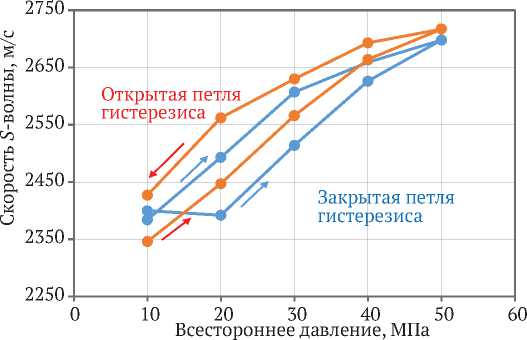
На рис. 5 представлена скорость P -волны в зависимости от всестороннего давления в сухом и водонасыщенном песчанике при постоянной амплитуде деформации. С увеличением всестороннего давления от минимальной до максимальной величины как в сухом, так и смоченном песчанике скорость волны нелинейно возрастает на 15,06 и 26,35 % соответственно. В обоях случаях наблюдается незамкнутая петля гистерезиса: для сухого песчаника – 9,77 % и смоченного – 15,93 %. На рис. 6 показана скорость S -волны в зависимости от всестороннего давления в сухом и водонасыщенном песчанике на постоянной амплитуде деформации. Здесь увеличение скорости волны идет так же, как и в случае P -волны, и составляет для сухого песчаника 12,42 %, а для смоченного – 15,81 %. Незамкнутый гистерезис для сухого песчаника составляет 0,67 %, а для смоченного – 3,45 %.

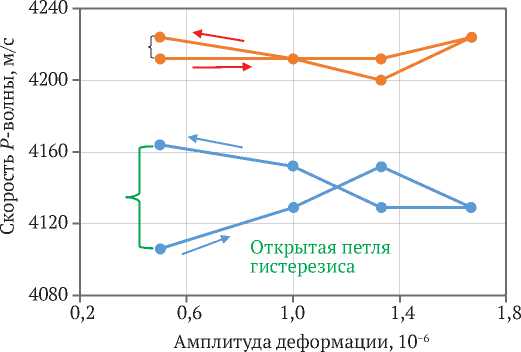
—•—Vp-сухой —•—Vp-водонасыщенный

Рис. 1. Скорость P -волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике

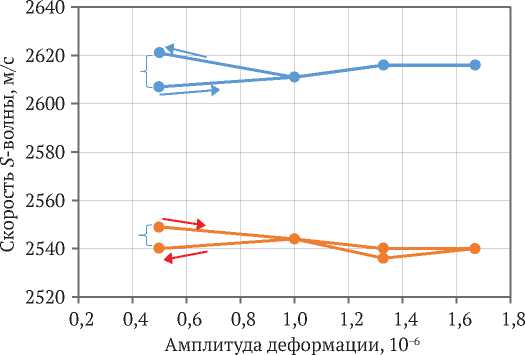
—•—Vs-сухой —е—Vs-водонасыщенный

Рис. 2. Скорость S -волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике

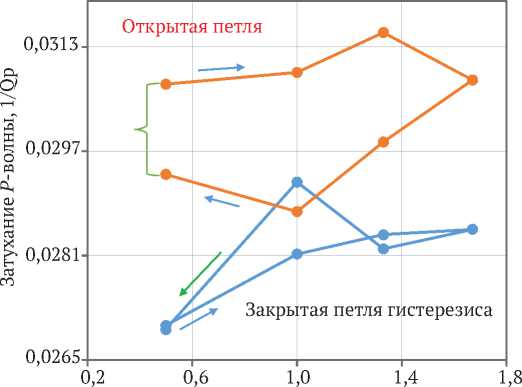
Амплитуда деформации, 10-6

—•— 1/Qp-сухой —•— 1/Qp-водонасыщенный

Рис. 3. Затухание P -волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике

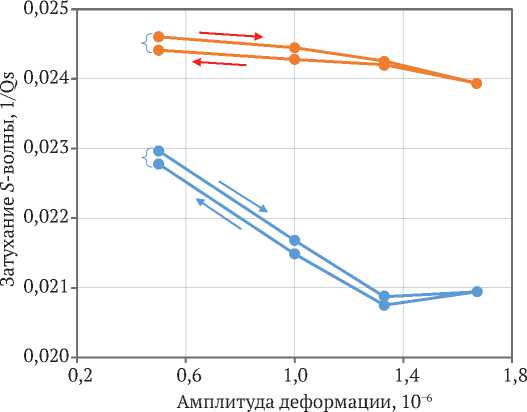
—•— 1/Qs-сухой ^^ 1/Qs-водонасыщенный

Рис. 4. Затухание S -волны в зависимости от амплитуды деформации в сухом и водонасыщенном песчанике

2023;8(1):22–29

-е-Vp-сухой -е-Vp-водонасыщенный

Рис. 5. Скорость P -волны в зависимости от всестороннего давления в сухом и водонасыщенном песчанике

—е-Vs-сухой -•-Vs-водонасыщенный

Рис. 6. Скорость S -волны в зависимости от всестороннего давления в сухом и водонасыщенном песчанике

Обсуждение результатов

Проведенное исследование показывает сложное влияние амплитуды деформации, давления и состояния песчаника на поведение скорости и затухания P - и S -волн. Затухание волны по сравнению со скоростью волны более чувствительно к девиации амплитуды и смоченного состояния песчаника. Поведение скорости продольной волны существенно отлично от поперечной. Измерение скорости P -волны показывает, что смена состояния песчаника влияет на форму гистерезиса и величину его открытия. Открытая часть гистерезиса для продольной волны в сухом песчанике составляет 1,41 %, а в смоченном 0,28 %, т.е. имеется большое различие между ними. Скорость S -волны как в сухом, так и смоченном песчанике, слабо реагирует на девиацию амплитуды.

Наибольшее изменение величины затухания продольной волны за счет амплитуды деформации получено в сухом песчанике (5,43 %) и том же состоянии на поперечной волне (8,81 %). Изменение величины затухания поперечной волны в смоченном песчанике за счет амплитуды достигает 2,71 %. На продольной волне открытый гистерезис зарегистрирован в смоченном песчанике (4,5 %), в сухом он отсутствует. На поперечной волне как в сухом, так и смоченном песчанике проявление открытого гистерезиса незначительно. Изменение всестороннего давления в замкнутом режиме как для продольной, так и поперечной волны приводит к нелинейному возрастанию скорости и появлению незамкнутой петли гистерезиса. Стоит отметить, что скорость продольной и поперечной волн при обоих состояниях песчаника реагирует на изменение величины всестороннего давления.

Заключение

Анализ полученных в эксперименте новых данных показывает сложный характер поведения скорости и затухания продольной и поперечной волн в зависимости от величины амплитуды деформации и сухо-водного состояния песчаника. Изменение амплитуды деформации и всестороннего давления по замкнутому циклу (то есть ее увеличение и адекватное уменьшение) приводит к существенному изменению динамических характеристик регистрируемого сигнала. Это преобразование имеет место для скорости волны и затухания. Влияние амплитуды деформации на гистерезис открытого и закрытого типа происходит как для скорости волны, так и для затухания. Как в сухом, так и смоченном песчанике в большинстве случаев наблюдается открытая петля гистерезиса. Имеются случаи проявления закрытой петли гистерезиса и также эффект перехлеста петлей гистерезиса. Наибольшее изменение скорости волны за счет амплитуды деформации получено для продольной волны в сухом песчанике. Однако параметр затухания превышает достижения скорости волны. Наибольший результат для амплитудно-зависимого затухания получен для сухого песчаника при распространении продольной волны – 5,43 % и при распространении поперечной волны – 8,81 %.

В нашем исследовании к признакам проявления микропластичности можно отнести следующее. Гистерезис открытого и закрытого типа, обнаруженный в амплитудно-зависимой скорости и затухании в сухом и смоченном песчанике. Нелинейный характер и перехлест восходящего и нисходящего курсов амплитуды. Их расхождение может быть вызвано эффектом микропластичности. Сложное и своеобразное поведение обеих петель гистерезиса предполагает возможность участия в процессе деформирования песчаника нестандартного механизма. Многообразное поведение скорости волны и затухания при деформировании горной породы может быть вызвано совместным действием процессов вязко-упругости и микропластичности. Качественные и количественные характеристики осложнений динамических параметров могут являться признаками внутреннего строения исследуемого объекта.

2023;8(1):22–29

2023;8(1):22–29

2023;8(1):22–29