Влияние асимметрии на развитие неустойчивостей в токовых слоях

В данной работе исследуется возможность развития разрывной тиринг - и кинк - неустойчивостей [1] ( с учетом симметрич ной и несимметричной мод ) в анизотропных тонких токовых слоях ( ТС ) [2]. В приближении линейной теории возмущения для уравнений Власова найдены профили возмущенных векторных потенциалов , инкременты нарастания неустойчивостей . Иссле довано влияние плазменной анизотропии и асимметрии токового слоя на развитие в нем данных неустойчивостей .

In this paper, a possibility for the development of tearing tiring- and kink-instabilities [1] (with regard to the symmetrical and asymmetrical modes) in anisotropic thin current sheets (CS) [2] is studied. Profiles of perturbed vector potentials and increments of instability increase have been found from the linear perturbation theory for the Vlasov equations. The effect of plasma anisotropy and asymmetry of the current sheet on the development of the above instabilities is investigated.

Разрывная неустойчивость , которая , как предпола гают , ответственна за начало пересоединения в ТС , была первоначально рассмотрена [3] в модели ТС Хар риса [4] в виде волнового возмущения вдоль магнитно го поля ~exp( ikx – i ω t ). Позднее линейная теория воз мущения была обобщена на случай ненулевой попе речной компоненты магнитного поля B _z ≠ 0 [5]. Элек троны , замагниченные компонентой магнитного поля B _z, не могут участвовать в резонансном взаимодействии с волной возмущения . В этом случае резонансное взаи модействие обеспечивается ионной компонентой плаз мы . Было показано , что для изотропных моделей ТС эффект электронной сжимаемости препятствует разви тию в токовом слое разрывной неустойчивости [6], поэтому такие слои являются полностью устойчивыми .

Таким образом , возникла необходимость исследо вания других моделей ТС на наличие разрывной неус тойчивости . Для модели анизотропного ТС [2] было показано , что в пространстве параметров системы { ε , b n } ( ε = ν T / ν D , b n = B z / B 0 , B 0 – магнитное поле на границе ТС ) существуют области отрицательных значений энергии тиринг - моды δ W ( рис . 1). В них ТС являются неустойчивыми . Области с δ W < 0 как функ ции волнового числа зависят от относительной толщи ны ТС L / ρ _i и величины нормальной компоненты маг нитного поля b_n . Для асимметричного ТС [7] области разрывной неустойчивости сильно зависят от парамет ра r , определяющего степень асимметрии ТС ( рис . 2). Можно видеть , как с ростом асимметрии увеличивается неустойчивость ТС .

Анизотропия ТС оказывает существенное влияние на развитие в нем кинк - неустойчивости , что можно видеть

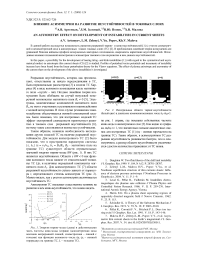
Рис . 1. Энергия тиринг - моды ( слева ) и действительная часть частоты кинк - моды ( справа ) ( асимметричная мода показана непрерывной линией , симметричная – линией с точками ) как функции волнового числа k ρ _i ( ρ _i – ионный гирорадиус на границе ТС , L – толщина ТС ).

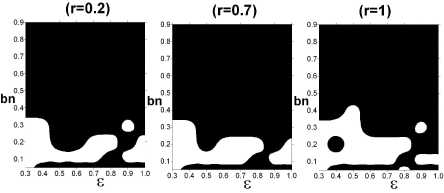
Рис . 2. Интегральные области тиринг - неустойчивости ( белый цвет ) в диапазоне изменения волновых чисел b_n < k ρ _i<1.

на рис . 1 справа , где показаны собственные частоты кинк - моды в анизотропном слое [2]. Как видно из графи ка , ω _r / ω _i << 1, что значительно меньше аналогичных оце нок для изотропных ТС [1] ( ω _i – ионная гирочастота на границе ТС ). Таким образом , в асимметричном ТС раз рывная неустойчивость развивается быстрее , чем в сим метричном , а размер области неустойчивости увеличива ется с ростом количества отраженных от ТС ионов .