Влияние атомов примеси на скорость диффузии лития в кристаллическом кремнии

Развитие литий-ионных аккумуляторов в настоящее время является одной из самых актуальных задач в области источников тока ввиду их перспективности, широкого использования в электронных устройствах и даже в автомобилестроении ближайшего будущего. По сравнению с другими перезаряжаемыми батареями, такими как кислотно-свинцовые, никель кадмиевые, и никель-металл гидридные, литий-йонные батареи обладают большим удельным зарядом, рабочим напряжением и меньшим током саморазряда. На сегодняшний день основным материалом анодов современных батарей является графит, который обладает адсорбционной емкостью по литию 372 мА∙ч/г, а также материалы на его основе. При внедрении ионы лития слегка раздвигают слои углеродной матрицы и располагаются между ними, образуя интеркалаты. Благодаря слабости Ван-дер-Ваальсовых взаимодействий между слоями sp2-гибридизированного углерода, удельный объем углеродных материалов в процессе интеркаляции-деинтеркаляции ионов лития меняется незначительно, что является положительной чертой данных материалов. К сожалению, в таких материалах происходит значительный перенос электрического заряда с атомов лития на слои графита, что ведет к существенному отталкиванию ионов лития. Это приводит к тому, что максимальное содержание лития в графите соответствует фазе LiC6, соответствующей вышеупомянутой адсорбционной емкости. Однако уже известно, что теоретическая емкость для батарей с кристаллическим кремниевым анодом может составить величину в 10 раз большую, чем для углеродных материалов [1], поэтому материалы на основе кремния сейчас широко изучаются как анодный материал для следующего поколения литий-йонных батарей [2–5]. Основной проблемой для широкого применения кремния в таких батареях является огромное увеличение объема кристаллической решетки кремния при его интеркалировании литием (~ 300 %), что приводит к быстрой деградации материала и малому количеству циклов сорбция-десорбция [6]. Одной из возможностей обойти данную проблему является использование наностуктур из кремния (наноусы и наночасти- цы), которые могут эффективно выращиваться, например, из газовой фазы методом CVD и др. В работах [7; 8] было убедительно продемонстрировано, что экспериментальные образцы с использованием кремниевых наноусов обладают в ~ 3 раза большими абсорбционными свойствами по сравнению с лучшими углеродными наноматериалами. Содержание лития в кремниевых наноусах и покрывающем их аморфном кремнии доходило до состава Li15Si4, причем кулоновская эффективность составляла ~ 90 % после 100 циклов зарядки. При этом именно использование наноусов, растущих в виде «леса» с выделенным направлением роста, позволило добиться малой деградации материала при значительном количестве циклов зарядка-разрядка. Малая деградация материала объяснялась тем, что значительные промежутки между отдельными наноусами (диаметром ~ 50 нм) не мешали «разбуханию» материала уса, внешняя оболочка которого за счет высокой скорости роста состояла из аморфного кремния, составлявшего в общей массе уса ~ 99 %. Тонкая кристаллическая сердцевина уса обеспечивала ему необходимую прочность и гибкость, а аморфное покрытие позволяло абсорбировать литий без разрушения структуры даже при большом разбухании решетки.

В недавних экспериментальных исследованиях было показано, что кристаллический кремний трансформируется в аморфный в процессе интеркаляции литием [9–13]. Результаты дифракции рентгеновский лучей (XDR) кристаллической фазы кремния максимально насыщенной литием при комнатной температуре, показали, что состав этой фазы не Li 21 Si 5 , как предполагалось ранее, а Li 15 Si 4 . Теоретическая адсорбционная емкость этой фазы равна 3579 мА∙ч/г, что хорошо согласуется с имеющимися экспериментальными результатами. При этом известно, что фазовая диаграмма систем Si–Li содержит достаточно большое количество кристаллических фаз [14; 15]. Известны фазы Li 21 Si 5 [16], Li 13 Si 4 , Li 14 Si 6 [17], Li 12 Si 7 [18] и LiSi [19; 20], однако они не возникают в процессе электрохимической интеркаляции/деинтер-каляции лития в кристаллический кремний [9–11].

Данные термодинамически стабильной фазы Si–Li обычно получаются в синтезе при высоких температурах (~ 700 К). Фазы, полученные электрохимическим методом и стабильные при комнатной температуре, предположительно являются аморфными сплавами чистого кремния и фазы кристаллического Li 15 Si 4 [21].

Одновременно с изучением системы Si–Li существуют экспериментальные работы, в которых проводилось изучение диффузии лития в твердых растворах Ge–Si [22]. Авторами было показано, что допирование кремния атомами германия приводит к увеличению скорости диффузии. Таким образом, допированные системы представляют интерес для дальнейших исследований. Их теоретическое исследование необходимо для лучшего понимания процесса сорбции в них лития и преодоления проблемы деградации материала в процессе циклической перезарядки. Поэтому целью данной работы являлось теоретическое исследование влияния атомов примесей на скорость диффузии лития в кристаллическом кремнии, которая в основном определялась величиной энергетического барьера для перехода атома лития между ближайшими минимумами энергии.

Все расчеты в работе проводились в рамках формализма функционала плотности (DFT) [23] с градиентными поправками Perdew-Burke-Ernzerhof (PBE) [24] с использованием лицензионного пакета VASP (Vienna Ab-initio Simulation Package) [25–28]. Данная программа для проведения ab-initio расчетов использует метод псевдопотенциала и разложение волновых функций по базису плоских волн. Для эффективного уменьшения количества базисных функций и увеличения скорости расчетов в программе для всех атомов использовались псевдопотенциалы Вандербильта (Vanderbilt ultrasoft pseudopotential) [29] с энергией обрезания E cutoff = 240 эВ. Для выбора оптимальных параметров расчета и точности интегрирования по первой зоне Бриллюэна был использован набор к-точек, сгенерированный с помощью метода Мон-хорста-Пака [30] на равномерной сетке 3X3X3, так как было обнаружено, что увеличение числа к-точек не приводит к увеличению точности расчета, но значительно увеличивает время расчета.

В первую очередь была оптимизирована геометрическая структура ячейки кремния в виде куба, включающая 64 атома и 1 атом лития, который располагался в потенциальном минимуме энергии – тетраэдрической поре. При проведении оптимизации геометрии координаты всех атомов в суперячейке варьировались с помощью метода сопряженных градиентов, используя вычисление сил, действующих на атомы. Оптимизация геометрии проводилась до тех пор, пока силы, действующие на каждый атом, не становились менее 0,05 эВ/Å.

Далее были рассчитаны высоты потенциальных барьеров (переходные состояния) для прыжков атомов лития. Данные расчеты были выполнены методом эластичной упругой ленты (NEB) [31]. Для этого были проведены оптимизации двух систем, где атом ли- тия последовательно находился в соседних тетраэдрических порах (потенциальных минимумах), и после этого найдена траектория движения атома лития (путь реакции) при переходе из одной поры в соседнюю. При этом были вычислены потенциальный профиль и величина барьера перехода атома лития через седловую точку потенциального профиля.

Расчет коэффициента диффузии проводили при помощи стандартного уравнения

D = — v a 2 , 2 Z

где a ² – квадрат длины прыжка атома лития между минимумами; v - частота его перескоков, которая в данном случае была получена из обобщенного уравнения Веньярда [32], учитывающего энергию нулевых колебаний. Данное уравнение позволяет рассчитывать частоту v перескока атома через потенциальный барьер:

— Ebarrier v = Ae kT ,                    (2)

где А – предэкспоненциальный фактор, определяемый следующим образом:

A =

h 3 N — 4

3 N — 3

IT П 1 ¹ kT i = i I

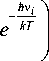
П 1 — e

i = 1

h v i

kT

'

где T - температура; v i и v i

– частоты всех собст-

венных колебаний системы для атома лития в локальном минимуме и седловой точке соответственно. При этом в положении седловой точки атом лития находится в максимуме энергетического барьера между двумя локальными минимумами – центрами тетраэдрических пор кремния. В данной работе, ввиду большого количества атомов в системе, частоты колебаний были рассчитаны для атома лития и его ближайшего окружения, включающего первую координационную сферу начального и конечного положения (9 атомов). Данное приближение было нами успешно использовано ранее [33].

Рассчитанное значение коэффициента диффузии лития в кристаллическом кремнии D = 3∙10^–3exp(–0,605 × × [eV] / kT ) неплохо согласуется с полученным экспериментально D = 2,5∙10^–3exp(–0,655[eV] / kT ) в работах [34; 35].

Далее было исследовано влияние атомов примесей (Al, B, C, Ge, P) на высоты потенциальных барьеров при движении атома лития около близкорасположенного атома примеси. На рис. 1 представлены энергетические профили реакции перехода атома лития между тетраэдрическими пустотами вблизи этих примесей. При этом атом примеси располагается поперечно и принадлежит одному из тетраэдров, поэтому начальная и конечная энергия для перехода атома лития неэквивалентны. Из графика видно, что величина барьера прямого и обратного перехода лития различ- на за счет разной энергии систем в начальном и конечном положениях.

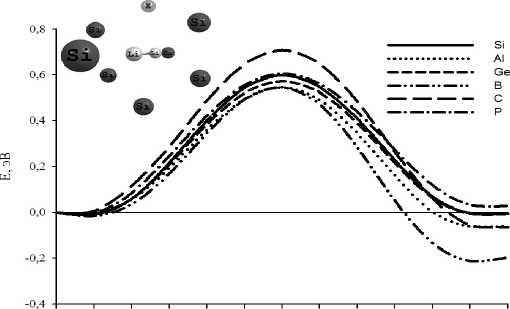
Рис. 1. Профиль потенциального рельефа для перехода атома лития между ближайшими минимумами в структуре XSi63Li, X = (Al, B, C, Ge, P, Si). Атом примеси находится перпендикулярно к направлению прыжка

Для кристаллической структуры кремния без примеси энергии перехода атома лития во всех направлениях: ∆ E пр = ∆ E обр = 0,605 эВ. Для дальнейшего рассмотрения в качестве примеси были выбраны атомы Al и Ge, так как для них величины барьера были минимальны: барьер для прямого перехода атома лития с примесью алюминия составил ∆ E _пр(Al) = 0,546 эВ, а обратный – ∆ E обр (Al) = 0,605 эВ. В присутствии примеси германия барьеры равнялись ∆ E пр (Ge) = 0,573 эВ и ∆ E обр (Ge) = 0,580 эВ. Наличие атомов фосфора не приводило к снижению энергии барьера перехода, а в случае B и C барьеры значительно увеличивались (на 0,14–0,17 эВ).

Далее было исследовано влияние на величину барьера для перехода лития двух близкорасположенных атомов примесей. Два атома примеси располагались в поперечном положении к атому лития напротив друг друга. В данном случае начальное и конечное состояния системы были эквивалентны по энергии, поэтому профиль потенциального рельефа перехода атома Li был симметричным (рис. 2).

В работе также было исследовано влияние на величину барьера перехода близкорасположенных атомов примеси, которые находились вдоль направления перемещения атома лития (рис. 3).

При этом данный барьер также соединяет неэквивалентные положения в минимумах. Однако при использовании в качестве примеси атома Ge начальное и конечное состояния отличаются на 0,02 эВ. Такое незначительное изменение можно объяснить тем, что Ge, как и Si, имеют схожую электронную конфигурацию и одинаковую алмазоподобную решетку. Только параметр решетки германия (a = 5,66 Å) больше, чем параметр для кремния (a = 5,43 Å). Только примесь в виде атома Al в данном положении значительно увеличивает энергетический барьер.

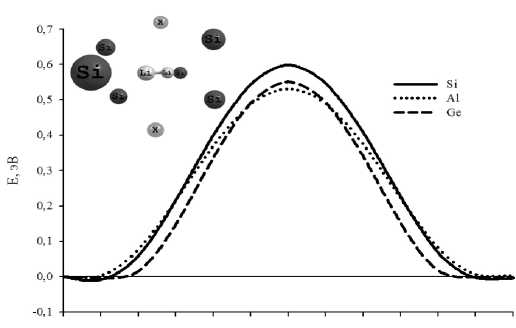
Рис. 2. Профиль потенциального рельефа для перехода атома лития между ближайшими минимумами в структуре X ₂Si₆₂Li, X = (Al, Ge, Si). Атомы примеси находятся перпендикулярно к направлению прыжка

Рис. 3. Профиль потенциального рельефа для движения атома лития между ближайшими минимумами в структуре X Si₆₃Li, X = (Al, Ge, Si). Атом примеси находится в продольном положении к направлению прыжка

В таблице представлены значения высот потенциальных барьеров перехода атома лития и коэффициенты диффузии в зависимости от типа и положения атомов примеси.

Высота потенциального барьера и коэффициент диффузии лития

Атом примеси	Положение атома примеси	Высота потенциального барьера, эВ	Коэффициент диффузии при T = 300 K, см2/с
Al	Поперечное	0,605	1,4∙10–13
	Продольное	0,790	1,5∙10–16
	Поперечное (2 атома)	0,532	2,6∙10–12
Ge	Поперечное	0,580	4,1∙10–13
	Продольное	0,610	1,3∙10–13
	Поперечное (2 атома)	0,553	1,5∙10–12
B	Поперечное	0,743	7,7∙10–16
C	Поперечное	0,772	3,6∙10–16
P	Поперечное	0,606	1,5∙10–13
Чистый Si	–	0,605	1,7∙10–13

Выполненные квантово-химические расчеты показывают, что коэффициенты диффузии лития в кристаллическом кремнии могут изменяться под влиянием близкорасположенных атомов примесей. Для ускорения диффузии лития могут применяться добавки в виде алюминия и германия. Внесение этих атомов в кремний ускоряет диффузию лития в ~ 4 раза при Т = 300 К. При этом показано, что увеличение концентрации примесей, т. е. возможность существования двух атомов примеси в окрестности атома лития, существенно увеличивает этот эффект.