Влияние ближнего разряда молнии на линию передачи

Проблема электромагнитной совместимости технических сооружений с атмосферным электричеством в условиях многолетней мерзлоты имеет особую актуальность. Одним из аспектов этой проблемы являются вопросы повышения эффективности грозозащиты линий передач. При разряде молнии вблизи кабеля между оболочкой и жилой кабеля возникают кратковременные перенапряжения, или вызванные прямым попаданием молнии, или индуцированные. Методы защиты от прямых ударов молний достаточно хорошо разработаны. Однако в регионах с высоким удельным электрическим сопротивлением грунта, к которым относятся и регионы с многолетней мерзлотой, часто наблюдаются множественные повреждения подземных кабелей вдали от точки разряда молнии даже при отсутствии прямого попадания молнии в кабель.

Общепринятый метод приближенного расчета индуцированных перенапряжений в воздушных линиях основан на вычислении электромагнитного поля, излучаемого каналом молнии. Это связано с решением системы уравнений Максвелла. С другой стороны, под действием электростатического поля грозового облака на проводниках линии передач индуцируются электрические заряды. При быстром разряде грозового облака эти заряды «высвобождаются» и, растекаясь по линии передач, образуют волну тока и напряжения (ВТН), в результате которой появляются так называемые грозовые перенапряжения. По мнению авторов, при отсутствии прямого попадания молнии основной причиной повреждений подземных кабелей, протянутых в плохо проводящей земле, является возникновение ВТН. Явление ВТН также может инициировать аварийные явления в ЛЭП и трубопроводах, расположенных в регионах с многолетней мерзлотой. Есть сведения о том, что на линии передач, расположенные в полярных и субполярных широтах, интенсивные геомагнитные возмущения оказывают сильное влияние, вплоть до аварий.

В предыдущих работах авторов аналитически и численно решены задачи о ВТН в предположении о мгновенном характере разряде молнии, рассмотрены случаи разряда молнии в землю и между двумя облаками [1; 2]. В нашей работе [3] представлена математическая модель ВТН, учитывающая зависимость тока молнии от времени и аналитически решена задача о ВТН. В данной статье приведен другой вид решения для случая произвольных погонных параметров R , C , L , G , проведены новые численные расчеты.

Математическая модель. Рассмотрим линию передач с одним проводником. Ось x направим вдоль этого бесконечного проводника. Проводник характеризуется распределенными параметрами R,C,L,G – сопротивлением, емкостью, индуктивностью и коэффициентом утечки, рассчитанными на единицу длины. Грозовое облако моделируем точечным зарядом Q, расположенным на высоте h над кабелем и на высоте h +1 над проводящим полупространством (проводящий слой земли), параметр l описывает толщину многолетнемерзлого слоя грунта. Следовательно, проводник находится в поле заряда и его электростатического изображения (рис. 1).

Рис. 1. Геометрия модели

Проводник считаем заземленной в бесконечно удаленной точке, потенциал Земли v = 0 , т. е. индуцированные на проводнике заряды создают такой потенциал, который компенсирует потенциал, создаваемый двумя точечными зарядами Q и - Q .

Пусть в момент времени t = 0 облако начинает разряжаться, зависимость заряда облака от времени выражается функцией Q(t), t > 0, тогда ток молнии равняется dQ(t) / dt. При уменьшении заряда облака на dQ за время dt те заряды на линии, которые компенсировали потенциал заряда dQ (и его изображение –dQ), стано- вятся свободными и начнут «разбегаться», возбуждая ВТН в линии. Другими словами, разряд грозового облака эквивалентен действию некоторого источника зарядов в линии. За время dt на элементе dx этот источник вырабатывает количество зарядов dq1, равное dq1 = Cdxdu = Cf (x) dxdQ, (1)

t--

X t ^{x - at}          a

+ — J d Z J *(Z, T) e

^{2 aC} x     0

k (t - 1 )

где

( t - t)²

( x - Z)²

f ( x ) =-- r=

⁴ⁿS o ( 4h

i

। „ 2

V(2 l + h )² + x² ₇

такой вид функции соответствует тому, что заряд нахо-

Rae

+---

(

XI 0

k

k J(t - t)² - ' x -' V              a

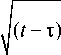
( x - Z)² '

„ 2

,л / t ^x + ^a ( t ^{- T} )

— J ^d t  J e ^/: y^T) I 0 ^x

0 x - a ( t - t)

d t +

дится над началом координат.

Аналогично [4] выведем систему телеграфных уравнений с учетом действия такого источника зарядов. Применяя закон Ома к участку длиной dx , получаем

x k. f( t - t)² -

( x - Z)² ' a²

d Z,

- u_x dx = iRdx + Li_t dx .                (3)

i ( x , t ) =

-

_ae - X t -----x

Количество зарядов, притекающих в элемент проводника dx за время dt равно

t xJ e" (*(x + a(t - t), t) - *(x - a(t - t), t))dt + 0

dq ₂ = ( i ( x , t ) - i( x + dx , t )) dt = - i x dxdt , за это время dt на участке dx за счет действия указанного выше «генератора» дополнительно образуется количество зарядов dq₁ . Количество заряда dq ₃ , которое идет на зарядку элемента dx за счет электроемкости равно dq ₃ = C ( u ( x , t + dt ) - u ( x , t )) dx = Cu t dxdt , количество заряда dq ₄ , теряющегося за счет несовершенства изоляции:

ke

-y t t     x ^{+ a} ( t - ^{t )}

+---- 2 a

J d T J   e "^T

0      x - a ( t - t)

x -Z

( t - t )²

x 1 ₁ ⁽ k I ( t - T ) ² - ^ x -^^)^ V             a

RC + LG 2 LC

( x - C )² a²

W ( Z , T ) x

d C

dq ₄ = Gudxdt .

Согласно закону сохранения заряда, dq₁ + dq ₂ = dq ₃ + dq ₄ .

Подставляя сюда выражения для зарядов, получаем Cf ( x ) dxdQ - i x dxdt = Cu t dxdt + Gudxdt .

Из этого соотношения и уравнения (3) получаем искомую неоднородную систему телеграфных уравнений и, добавляя нулевые начальные условия, получаем задачу Коши, описывающую ВТН в линии передачи, с учетом зависимости тока молнии от времени:

I RC ^- LG a 2 = k = 2 LC ' LC '

Рассмотрим неискажающую линию передачи, т. е. когда погонные параметры удовлетворяют соотношению RC = LG . В этом случае

R

^X = ^- L, k = 0, и формулы для величин ВТН существенно упрощаются:

-

u + Lit + Ri = 0, -^ > x xt ix + Cut + Gu = Cf (x) dQ, u(x,0) = 0, i(x, 0) = 0.

t >  0,

x - at x + at /x r , Z - x 1 ■ x *1 Z, tI

a x k7

- X^-x       1

^a d Z +----x

2 aC

-

X^^-^ ^a d Z,

Аналитическое решение . Аналитическое решение задачи (4), описывающей ВТН, получаем в следующем виде:

i _{( x t} ) _{= -} ^{ae X} t \e"^{X T (} * ⁽ x ⁺ a ⁽ t - t),t) - ¹ ’ ^J 2 ^J ₀ - *( x - a ( t - t), t)) d t .

λ t e^t

+--

2 aC

x - at x + at / x J * ( x

Z - x t + ---- xa

x                     1

a d Z + x 2 aC

— 1

( г

-

X^-x ^a d Z +

Прямоугольный импульс тока молнии . Рассмотрим случай, когда ток молнии имеет вид прямоугольного импульса с длительностью 1 ₀ , с амплитудой 1 ₀ = Q ₀ / 1 ₀ , где Q ₀ - первоначальный заряд облака, в этом случае заряд облака выражается функцией

Q (t) = Q0(1 -1 )n( 10 -1), t0

где

J d Z J *(Z, T) eXI o k J(t - t)² -

x - at 0

k (t - t )

'(t - T)2 - a

k

1 1 ⁽ k J ( t - T)² - ^ x -Д v              a

( x - Z)² a²

1'

d t +

= (1, при t >  0, ¹ { 0, при t <  0

- единичная функция Хевисайда.

Тогда dQ^ -Q n(10 -1) dt         10

откуда

V( x , t ) = Cf ( X )

dQ ( t )

^^^^^^B

dt

CQ^ ^{f ( x} )П ⁽ t 0 ^- t )- t 0

Таким образом, решение (5) задачи (4) будет иметь

следующий вид:

x u (x, t) = - Q^- J f (Z)n 110 -1 2aC x J at       k

^^^^^^в

^z - ^x

-xi^x

e

a

-

Q 0 e

2 at ₀

a

d ζ

^^^^^^в

над ущельем), R = 10 ³ Ом/м, C = 10 ¹⁰¹ Ф/м, L = 10 7 Гн/м, G = 10 ^{6    1} .

Ом ■ м

Результаты расчетов в разные моменты времени для безразмерной силы тока и напряжения при разряде молнии в землю приведены на рис. 2,3-

+

-

-

x + at           /            i, \

-Q ^ f f (Z)n 1 1 ₀ - 1 + ^ - x I e

2 aC x k ⁰ a J

-xi^x

a

d Z -

x

Z - x t + -----

a

J d Z J f (Z) eX1 0 kJ(t - t)² -

( x - Z)²

x

at

k

A

k ( t - t)

( t - t)²

Q 0 e' t x

—

^^^^^B

at

( x - Z) ²

a ²

t

—

Z-x

a

a a

2 at ₀

+

k ( t - t)² -

( x - Z) ²

a a

П⁽ t о ^{- t) d t}

-

(

(

J d Z J f (Z) e    (-X) I о kJ ( t - t)² -

( x - z)² A

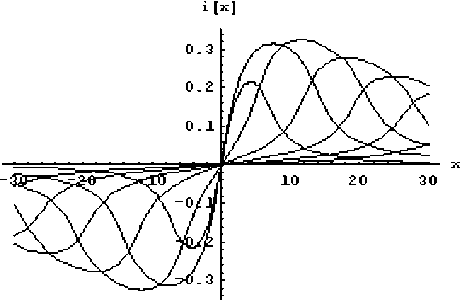
Рис. 2. Волна силы тока для прямоугольного импульса тока молнии

x

k

A

k ( t - t)

a2

( t - t)²

^^^^^B

( x - Z)²

I 1 k .И t - t)² -

( x - Z)²

a2

П⁽ t

-

t) d t

-

^^^^^^B

a a

RCQ0 ae

- X t t

x + a ( t

J ^{d T} J

t)

e ' f (Z) I о x

x k. (tt - t)² -

x - a ( t - t) ( x - Z)² A

a a

П ⁽ t о ^{- t) d Z.}

Аналогично преобразуется формула (6) для силы тока:

i ( x , t ) =

Q 0 Cae ^{- X t}

x

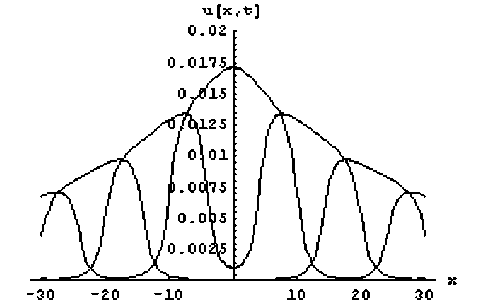
Рис. 3. Волна напряжения для прямоугольного импульса тока молнии

x

f e ^{X t} (y( x + a ( t - t))

J - y( x - a ( t - t))) n( t₍

-

-

t) d t

-

kQ o Ce

, - X t t

x + a ( t - t)

2 at ₀

J ^{d t} J

e

- Xt

x

-

ζ

x

a ( t

t)

( t - t)²

^^^^^^B

( x - Z)²

^x

x 1 1 k. (tt - t)² -

( x - z)² A

a

a a

d Z.

В случае неискажающей линии передач решение (7), (8) будет иметь вид

x

u ⁽ x , t ) = ^-        J

² at 0

^{f (Z)} n l t

-

t

-

e

x + at          / x J f (Z)nl 10 -1- x

ζ x

- X----

■ a d Z -

Z - x ) - I e

a

2 at

i ( x , t ) =

Q 0 Cae

- х5л^

' a d

’ ^X t fe ^Xt (v( x + a ( t - t)) -

^{J -} V ^{( x -} a ⁽ t ^{- t)))} П ⁽ t 0 ^{- t) d T-}

Численные расчеты . Численные расчеты проведены для случая прямоугольного импульса тока молнии с длительностью 1 ₀ = 50 мкс и амплитудой J ₀ = 20 кА , Q ₀ = 1 Кл при h = 1 500 м, l = 250 м (сухой грунт над вечной мерзлотой или скальный грунт, воздушная линия

Расчеты показывают, что максимальное значение силы тока в линии при приведенных выше параметрах достигается в точках, расположенных на значительном расстоянии. Сравним полученные результаты с результатами расчетов по модели с мгновенным разрядом молнии [5]. Распределения силы тока в линии при достижении ее максимального значения, рассчитанные по этим двум моделям при одинаковых параметрах, приведены на рис. 4

Видно, что максимум тока в модели с мгновенным разрядом молнии в несколько раз больше, чем в модели с учетом зависимости тока молнии от времени. Видны и различия в крутизне переднего фронта волны. Максимальные значения силы тока достигаются в разные моменты времени.

Распределения напряжения в линии при достижении ее максимального значения, рассчитанные по этим двум моделям при одинаковых параметрах, приведены на рис. 5.

Таким образом, в работе построена математическая модель ВТН, существенно отличающаяся от общепринятых моделей расчетов индуцированных перенапряжений [6; 7], в которых принято вычислять горизонтальную составляющую электрического поля излучения канала мол-

нии вблизи линии передачи. Численные расчеты по этой модели показывают, что предыдущая модель авторов с мгновенным разрядом молнии дает завышенные значения для величин ВТН. Ясно, что приведенная в данной работе модель с учетом зависимости тока молнии от времени более адекватно описывает изучаемое явление.

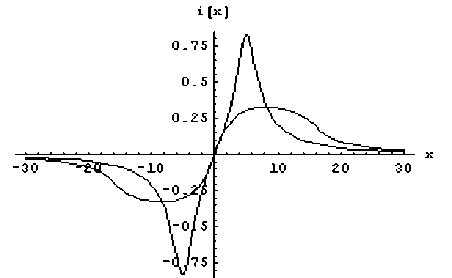
Рис. 4. Волны тока для двух математических моделей при достижении максимальных значений силы тока

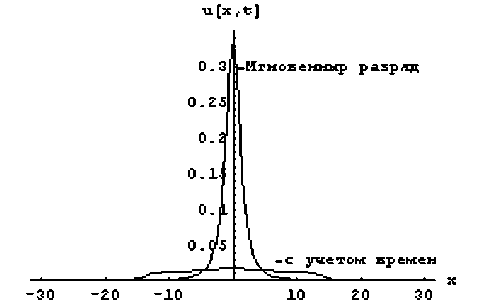
Рис. 5. Волны напряжения для двух математических моделей при достижении максимальных значений