Влияние частоты на параметры синхронной электрической машины

Представляет интерес поведение синхронных электрических машин при различном характере нагрузки. Для индуктивной синхронной электрической машины заслуживает внимания зависимость амплитуды тока и момента сопротивления вращению от нагрузки, для емкостной синхронной электрической машины – это зависимость амплитуды напряжения и момента сопротивления вращению.

Анализ состояния вопроса. Потокосцепление обмотки вращающей электрической машины равно

ψ = Ψ _m cos ω t .

ЭДС обмотки определяется выражением dψ e = -    = ωΨ sin ω t.

dt ^m

Амплитуда ЭДС

Em = ®* m зависит от частоты, в связи с чем может возникнуть интуитивное предположение, что амплитуды тока и момента сопротивления вращению для индуктивной синхронной электрической машины (амплитуды напряжения и момента сопротивления вращению для емкостной машины) также зависят от частоты. В действительности это не является закономерностью. Существенную роль при этом играет характер нагрузки электрической машины.

Цель исследования – показать, при каком характере нагрузки параметры синхронной электрической машины не зависят от частоты.

Задачи работы – получить доказательные на уровне теорем результаты.

Актуальность работы обусловлена широким распространением синхронных электрических машин, используемых, в частности, в качестве генераторов [1–3].

Методы исследования

В настоящей работе применяются методы математического моделирования.

Результаты и обсуждение

Ток и момент сопротивления вращению индуктивной синхронной электрической машины при индуктивной нагрузке

Пусть нагрузкой фазы индуктивной синхронной электрической машины является катушка индуктивности [4]. Суммарная индуктивность катушки и обмотки машины обозначается L. Число витков обмотки – n. Длина активной части витка – l. Индукция магнитного поля в рабочем зазоре – B. Угол поворота ротора - ф. Частота вращения - ш = dф/dt. Ток - i. Число полюсов - два. Диаметр ротора - Dr. Активные электрические и механические потери не учитываются.

Для синхронной машины с индуктивной нагрузкой справедлива следующая теорема.

Теорема 1. Амплитуда тока в индуктивной нагрузке индуктивной синхронной электрической машины не зависит от частоты вращения.

Доказательство. При указанных допущениях справедливо равенство (второй закон Кирхгофа и закон электромагнитной индукции применительно к вращающей машине)

D_r d ф         di

Bln r sin ф = L .

2 dt          dt

Интегрирование этого выражения дает

I =

Bln D _r

L 2

cos ф + 1 0 = - I _m cos ф + 1 0 .

Начальный ток I 0 можно считать равным нулю. Амплитуда тока

_I _ BlnD _r ” = L 2

от частоты вращения ω не зависит. Теорема доказана.

Теорема 2. Амплитуда момента сопротивления вращению для индуктивной синхронной электрической машины с индуктивной нагрузкой не зависит от частоты вращения.

Доказательство. При указанных допущениях момент сопротивления вращению в соответствии с законом Ампера (применительно к вращающей машине) равен

D           Bln D D         ( Bln ) ² D ²

µ = Blni ^r sin ϕ = -Bln ^r cos ϕ ^r sin ϕ = - ^r sin 2 ϕ .

2             L 2      2           L 8

Амплитуда момента сопротивления вращению

M m

( Bln )² D r ²

L 8

от частоты вращения ω не зависит. Теорема доказана.

На рисунке представлена схема синхронной электрической машины с индуктивной нагрузкой.

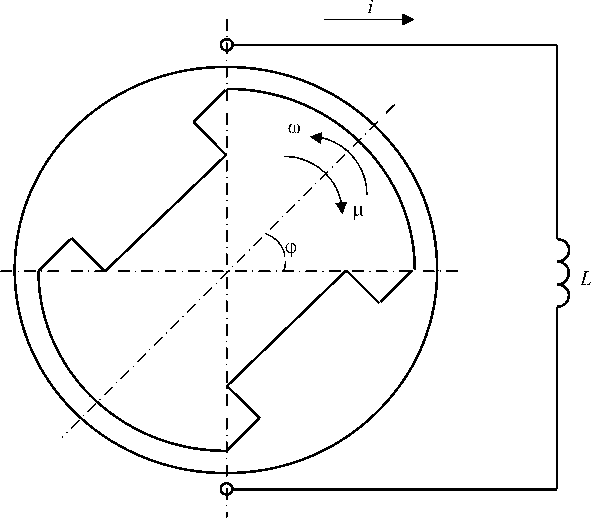
Рис. Схема синхронной электрической машины с индуктивной нагрузкой Fig. The circuit of the synchronous electric machine with inductive load

Правомерен вопрос – как обстоит дело при другом характере нагрузки синхронной электрической машины?

Ток и момент сопротивления вращению при активном и емкостном характере нагрузки При активной нагрузке аналог уравнения (1) имеет вид

Bln ^r ^- sin m = Ri .

2 dt

Амплитуда тока

Bln D

Im =--® m R2

от частоты вращения ω зависит (линейно).

Момент сопротивления вращению равен

D        Bln D

D         ( Bln )² D ²

^r sinϕ = ^r ω sin 2ϕ.

2          R 8

µ = Blni ^r sin ϕ = Bln ^r ω sin ϕ

2           R 2

Амплитуда момента сопротивления вращению

M. = (Bln) 2 m R

D ²

—- to

от частоты вращения ω зависит (линейно).

При емкостной нагрузке [5–7] аналог уравнения (1) имеет вид

D             1 ^t

Bln —- to sin to t = — idt.

2           C ^∫ 0

Дифференцирование этого выражения дает

D i = BlnC — ю cos юt, 2

Амплитуда тока

, D .

I = BlnC -m m 2 m ₂

от частоты вращения ω зависит (квадратично).

Момент сопротивления вращению равен

D           D      D           D ²

µ = Blni ^r sinϕ = BlnBlnC ^r ω ² cosϕ ^r sinϕ = (Bln) ² C ^r ω ² sin 2ϕ.

Амплитуда момента сопротивления вращению

M „ = ( Bln)¹ GD- to²

от частоты вращения ω зависит (квадратично).

Связь мощности с частотой при различных видах нагрузки

Для индуктивной нагрузки реактивная электрическая мощность равна

Q = 1 ² X = 1 2 ® L = (-ln-- r- ш ,

L где I – действующее значение тока.

Механическая мощность [8] равна

( Bln ) ² D¹ Qm = M to =--- to .

M          L 8

Как мы видим, (2) и (3) совпадают.

Мощность линейно зависит от частоты.

Для резистивной нагрузки активная электрическая мощность равна

Р = ₇ 2 r = (_K DL _ф 2 .

R 8

Механическая мощность равна

P M

= M to =

( Bln ) ² D r ² 2 --to .

R 8

Разумеется, (4) и (5) совпадают.

Мощность квадратично зависит от частоты.

Для емкостной нагрузки реактивная электрическая мощность равна

Q = 1 ² X_c = 1 ²--- = (Bln) ² CD- m 3 .

C     mC          8

Механическая мощность равна

q = m rn= ( Bln)² Cd- rn ³ .

Очевидно, что (6) и (7) совпадают.

Мощность кубично зависит от частоты.

Напряжение и момент емкостной синхронной электрической машины при емкостной нагрузке

Дуальным аналогом индуктивной синхронной электрической машины является емкостная синхронная электрическая машина.

В соответствии с законом магнитоэлектрической индукции (дуальный аналог закона электромагнитной индукции) ток равен

i = Dbv ,

где D – электрическая индукция (электрическое смещение) в рабочем зазоре, b – ширина электрода, v – линейная скорость.

Выражение (8) можно преобразовать следующим образом:

dq = Db dx dt dt dq = Dbdx , qx

∫ dq = Db ∫ dx , 00

q = Dbx .

С учетом последнего уравнения сила, действующая на электрод, равна

F = qE = q ^u = Dbu. x

Это дуальный аналог закона Ампера для электрического (магнитоэлектрического) взаимодействия. Здесь Е – напряженность электрического поля, u – напряжение. Электрический ток равен i = C du .                                               (10)

dt

Замечание. Формулы (8) и (9) могут быть получены из их электромагнитных аналогов путем простой дуально-инверсной замены величин e → i , B → D , l → b , i → u [9; 10].

Теорема 3. Амплитуда напряжения на емкостной нагрузке емкостной синхронной электрической машины не зависит от частоты вращения.

Доказательство. Для вращательной машины уравнение для тока с учетом (8) и (10) имеет вид

D d ф . du Db — — sin ф = C — .

2 dt           dt

Интегрирование этого выражения дает

Db D

u = ———— cos ф + U 0 = - U m cos ф + U 0 .

Амплитуда напряжения

U = Db Dr m C2

от частоты вращения ω не зависит. Теорема доказана.

Теорема 4. Амплитуда момента сопротивления вращению для емкостной синхронной электрической машины с емкостной нагрузкой не зависит от частоты вращения.

Доказательство. Момент сопротивления вращению в соответствии с (9), (11) и (12) применительно к вращающей машине равен

ц = Dbu-^-sinф = -DbUm cos ф-^rsinф =-Db

Db D    D

--- cos Ф —- sin Ф =

C 2      2

_D 2 _b 2 _D 2

--- Sln2 ф .

C 8

Амплитуда момента сопротивления вращению

Mm

D ² b ² Dr ²

C8

от частоты вращения ω не зависит. Теорема доказана.

Выводы

Таким образом, вопреки возможному интуитивному предположению для индуктивной синхронной электрической машины с индуктивной нагрузкой амплитуды тока и момента сопротивления вращению от частоты вращения не зависят. Наряду с этим, как показали исследования, амплитуды тока и момента сопротивления вращению зависят от частоты вращения при активном и емкостном характере нагрузки. Для емкостной синхронной электрической машины с емкостной нагрузкой амплитуды напряжения и момента сопротивления вращению от частоты вращения не зависят.

Полученные результаты рекомендуется использовать при проектировании электрических систем.