Влияние числа куранта на результаты численного моделирования распространения сигналов в недиспергирующих однородных средах

Численные методы решения волновых уравнений играют важную роль не только в конкретных технических приложениях, но и в фундаментальной науке в целом. К таким методам относится и FDTD (Finite-Difference TimeDomain) [1], некоторые особенности которого и являются предметом данной работы.

Основное достоинство метода FDTD — простота реализации расчетного алгоритма. Именно это обуславливает широкое применение FDTD в самых разнообразных приложениях: биологии и медицине [2–5], экологии, геологии и минералогии [6, 7], оптике, фотонике, электронике, связи и телекоммуникациях [8–13]. Кроме множества статей, так или иначе связанных с методом FDTD, на эту тему имеется и обширная учебная литература [14–17].

Несмотря на давнюю историю развития, внимание исследователя по-прежнему привлекают фундаментальные основы метода FDTD. К числу этих основ относится и вопрос оценки корректности решений, полученных методом FDTD в разнообразных постановках задачи для сигналов с различной формой спектра [14, 17, 18].

Хорошо известно (см., например, учебную литературу [14–17]), что основным параметром, регламентирующим точность вычислений методом FDTD, является число Куранта, которое для 2D-случая (1 пространственное + 1 временное измерения) имеет вид

S c = c ^ t (1)

^ x и связывает вместе основной физический параметр c — скорость света в вакууме с численными параметрами задачи Ax и At, определяющими шаг дискретизации пространства-времени.

Замечание 1 . Качество численного решения определяется не только выбором значения числа Куранта S _c , но и требованием к спектральному составу сигнала, а также уровнем начального тока его источника (см. Утверждение 2 в нашей предыдущей работе [18]). Именно влиянию последних двух факторов и была посвящена статья [18], в которой число Куранта было выбрано оптимальным образом для моделирования электромагнитных процессов в вакууме, а именно — было положено, что S _c = 1 . Данное исследование является логическим продолжением работы [18].

E Z ⁺¹ [ m ] = E q [ m ] -J q ^{+ 2} [ m ]+

+ ^-П (Н У ^{+ 2} [ m + ¹ 1 - Н У + ²

£ r \ y L 2_ ^y

m -

а простейшие поглощающие граничные условия (21) из [18] заменены нами на более общие уравнения, построенные на основе дифференциальных уравнений адвекции электромагнитного поля второго порядка точности. Все детали реализации данной схемы подробно изложены в статье [18] и пособии [14].

Замечание 2 . Моделирование работы направленного источника тока в формализме TF/SF в данной статье также претерпело некоторые изменения по сравнению с [18] и сводится к вычислению полей по схеме

_{H y}q + ¹ 2

s -

= H y ²

s -

-     E nc [0 ,q ] , (4)

ηµ r ^z

. Г 1

E q ⁺1 [ s ] = E Z [ s ] + E - - ,q + ₉ .   (5)

V £ r M r L 2     2

1. Мотивация и цель работы

Выбор S _c = 1 в общем случае не обеспечивает качество получаемого численного решения в однородных недиспергирующих средах, оптически отличных от вакуума. Это можно легко увидеть, изучая рис. 1 и 2.

1.0

E z [m] 0.5

0.0

0    25    50    75   100   125   150   175   200

m

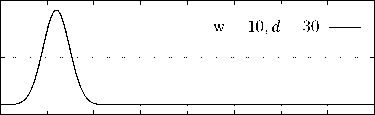
Здесь (как и в работе [18]) s = 50 — это фиксированный во всех численных экспериментах номер узла сетки, задающий расположение в пространстве точечной антенны, формирующей падающее поле E _z ^inc . Вычисление электрического E _z [ s ] и магнитного H _y [ s - 2] полей, согласно (4), (5) по заданному типу падающей волны E _z ^inc , позволяет имитировать работу источника тока J ^q , формирующего волну, излучаемую в правую область сетки m ⩾ s . В дальнейшем везде под работой источника тока J ^q будем иметь в виду именно эту схему.

1.0

J ^q 0.5

0.0

0    25    50    75   100   125   150   175   200

q

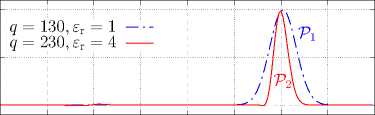
Рисунок 1. Моделирование распространения импульсов гауссова вида в вакууме P 1 и диэлектрике P 2 с относительной диэлектрической проницаемостью е _r = 4 .

Figure 1. Simulating of the propagation of Gaussian form pulses in vacuum P 1 and dielectric P 2 with relative permittivity е _r = 4 .

1.0

0.5

E _z [m]

0.0

-0.5

0    25    50    75   100   125   150   175   200

m

1.0

0.5 J ^q

0.0

-0.5

0    25    50    75   100   125   150   175   200

q

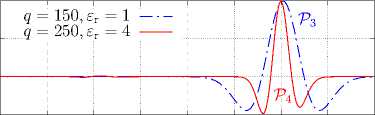
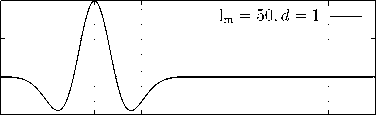
Рисунок 2. Моделирование распространения импульсов в форме вейвлета Рикера в вакууме P 3 и диэлектрике P 4 с относительной диэлектрической проницаемостью е _r = 4 .

Figure 2. Simulating of pulse propagation in the form of a Ricker wavelet in vacuum P 3 and dielectric P 4 with relative permittivity е _r = 4 .

Рисунки 1 и 2 построены в соответствии с алгоритмом Йи, подробно обсуждавшимся нами в предыдущей работе [18] (см. там формулы (13), (19)–(21)), с той разницей, что теперь уравнения обновления (19)–(20) в явном виде учитывают материальные параметры среды (а именно — ее диэлектрическую ε r и магнитную µ r проницаемости), в которой распространяются сигналы

_{H y}q + ¹ 2

m +¹ = H y

m +2 +

+    ( E Z [ m +1] - E Z [ m ]) ,

ηµ _r

Параметры источников тока J ^q , формирующих сигналы, представленные на рис. 1 и 2, также подробно описаны нами в работе [18] (см. там формулы (32)–(34) и соответствующий текст) и выбраны такими, чтобы импульсы P 1 и P 3 , распространяющиеся в вакууме, можно было считать корректным численным решением задачи в смысле Определения 2, данного в [18]. Исходя из этого, импульсы P 1 и P 3 можно считать «опорными», сравнивая с которыми

импульсы P 2 и P 4 соответственно, легко оценить влияние среды на корректность численного решения задачи.

Рисунки 1 и 2 построены при одном и том же значении числа Куранта S c = 1 , для которого в источнике [14] утверждается, что оно минимизирует численные ошибки FDTD-расчета, а в пособии [17] заявлено, что такой выбор позволяет получить точное решение задачи.

Вместе с тем, совершенно очевидно, что FDTD-решения, изображенные импульсами P ₂ на рис. 1 и P ₄ на рис. 2, не являются корректными в смысле Определения 2, данного нами в работе [18], что находится в явном противоречии с отмеченным в предыдущем абзаце. Эта некорректность есть результат явления, повсеместно возникающего при численных расчетах методом FDTD и известного в литературе [14, 17] под названием «численная дисперсия».

Действительно, сигналы P ₂ на рис. 1 и P ₄ на рис. 2 не представляют собой ни исходный гауссов импульс, ни вейвлет Рикера соответственно. При распространении данных волновых пакетов в диэлектрике с е _r = 4 за достаточно длительное время ( A q = 230 и 250 соответственно) их форма существенно исказилась (отметим, что этот эффект при использованных параметрах достаточно слаб и отчетливо начинает проявляться только к концу моделирования). Это противоречит изначальной математической модели симулируемого нами явления, так как среда полагалась нами недиспергирующей. Это явное противоречие порождает закономерный вопрос: может ли метод FDTD вообще использоваться для получения корректных результатов моделирования распространения сигналов в недиспергирующих материалах? И если это возможно, то как на корректность получаемых решений влияет выбор числа Куранта S _c ?

Несмотря на отмеченное выше противоречие, метод FDTD был использован нами ранее в ряде работ, в которых либо рассматривалось распространение волн в случайно-неоднородных средах [12, 13], либо исследовались особенности решения однородной и неоднородной задач Коши методом FDTD [18]. И в первом, и во втором случаях все проблемы, связанные с численной дисперсией, полностью игнорировались, что отчасти обусловлено тем, что во всех этих работах существенную часть трассы, вдоль которой рассматривалось распространение электромагнитных сигналов, представляло собой воздушное пространство (моделируемое нами неотличимым от вакуума). Вместе с тем, подобное игнорирование данной стороны дела не может быть полностью оправданным, что требует, если не полной корректировки численной дисперсии, то хотя бы уточнения эффектов, связанных с ней.

Далее отметим, что в книге [14] без каких-либо доказательств постулируется, что значение Sc = 1 — максимально возможное, что, вообще говоря, абсолютно не соответствует смыслу определения (1), которое не накладывает никаких ограничений на произвольно выбираемые пространственно-временные шаги сетки Ax и At и их соотношение между собой. В источнике [17] более осторожно утверждается, что выбор Sc > 1 приводит к экспоненциальному нарастанию шума, вызванному ошибками округления, всегда имеющими место при численном моделирова- нии, что в конечном счете полностью разрушает полученное решение.

Замечание 3 . Следует также отметить, что в работах [14] и [17] числами Куранта называются разные величины, что создает дополнительные трудности для понимания всех отмеченных вопросов. Это связано с тем, что в [14] в определении (1) величина c — это скорость света в вакууме (как принято и нами в данной работе), в то время как в [17] считается, что c — это скорость распространения волны в данной конкретной среде.

Кроме уже отмеченных проблем, также возникает вопрос о возможности применения метода FDTD для моделирования электродинамики в «не самых обыкновенных средах» (пусть и в пренебрежении явлением дисперсии). Здесь имеются в виду следующие примеры: распространение радиоволн в ионосфере Земли [19], электромагнитные волны терагерцового или рентгеновского диапазона в проводниках, полупроводниках или диэлектриках [20, 21], среды с отрицательными значениями относительных прони-цаемостей (в частности, «левые» среды [22–25]). Во всех этих случаях решающую роль играет дисперсия электромагнитных волн, аномальный характер которой с математической стороны дела состоит в том, что проницаемости ε _r и µ _r могут принимать значения, меньшие единицы, и даже более того, — отрицательные.

При этом обычные алгоритмы, встречающиеся в литературе по методу FDTD [1, 12–18], не позволяют моделировать распространение электромагнитных волн в таких средах, просто задавая значения 0 < е _r ,ц _r <  1 и е _r , р _r <  0 .

Решению отмеченных вопросов и посвящена настоящая статья, цель которой состоит, таким образом, в рас-смотрии численной дисперсии метода FDTD и оценке влияния выбора значений числа Куранта на качество моделирования распространения сигналов в однородных недиспергирующих средах.

• 2.    Численная дисперсия в методе FDTD

Для получения выражения, описывающего численную дисперсию в сетке Йи, вернемся к исходным дискретным аналогам уравнений Ампера (3) и Фарадея (2), которые в более компактной и удобной форме можно записать с помощью операторов сдвига в пространственно-временной сетке S _x ^χ и S _t ^τ (здесь χ и τ — параметры сдвига, имеющие форму х,т = р/ 2 , Ч р 6 Z ). Действие этих операторов по определению имеет вид

S X : S X ^ q [ m ] = ^ q [ m + X ] ,          (6)

S t : S t ^ ^q [ m ]= ^ q ^{+ T} [ m ] ,           (7)

где ψ обозначает произвольную компоненту электромагнитного поля (в рассматриваемом нами 2D-случае — E z или H y ).

Несложно проверить, что с помощью операторов (6) и (7) уравнение Ампера (3) в отсутствии сторонних источников ( J = 0 ) может быть записано в форме

1 _{S t} 2 _ε

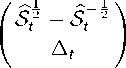
E z [ m ] =

/ bl     b^— 1 \

Утверждение 1. Дисперсионное соотношение для сетки Йи может быть представлено в форме

= b   ^S x -S x ² V q [ m ] .

x

sin

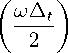
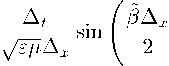
Здесь учтено определение числа Куранта (1), связь скорости света в вакууме с его диэлектрической е ₀ и магнитной ц ₀ проницаемостями с = 1 / ^ е ₀ М о и выражени е для характеристического импеданса вакуума П = V Ц ₀ /е ₀ ~ 120 п (для справки см., например, учебники [20, 21]). Кроме того, при записи (8) используется обозначение для абсолютной диэлектрической проницаемости среды е = е _r е ₀ .

Определим для удобства также конечно-разностные операторы ∂i согласно di = Si    Si   ,                   (9)

^ i

Доказательство. Используя результаты (14) и (15) Леммы 1, а также (16) в законе Ампера (10) для плоской монохроматической волны, запишем

iе-^— sin ( ^^t ^ e i“ ^д t/ ² E Z [ m ] =

— t     2          ^z

-i- — sin

— x

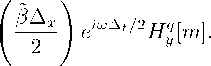
Подставляя в последнее равенство явные выражения полей (12), (13) для плоской монохроматической волны и сокращая общие множители, получаем

где i — это x или t . С помощью (9) закон Ампера в стационарной среде без сторонних токов (8) окончательно может быть записан в форме Йи [14]

е S t d _t E Z [ m ] = S t d _x H y [ m ] .         (10)

— | H_o.  (19)

2 J ⁰

Отсюда приходим к выражению для численного импеданса в сетке Йи

Таким же образом, с помощью (6), (7) и (9), дискретный аналог закона Фарадея (2) приводится к форме Йи

m S X d t H y [ m ] = S X d x E Z [ m ] .         (11)

E 0

H 0

_— е — _x

. в — X sin----- _____ 2

и — _t sin---- 2

Теперь рассмотрим плоскую монохроматическую волну частоты ω , распространяющуюся в сетке Йи вправо ( m ⩾ s )

E q [ m ] = E ₀ e i ⁽ “q △ ^{t — e}m ^д x ) ,          (12)

H q [ m ] = H 0 e i ⁽ “q ^{д t — e}m ^д x ) ,          (13)

где β — волновое число, т. е. постоянная распространения плоской монохроматической волны в FDTD-сетке (отличающаяся от соответствующей константы β в непрерывном пространстве), а E ₀ и H ₀ — комплексные амплитуды напряженности электрического и магнитного полей.

Лемма 1. Действие операторов (9) на произвольную компоненту ψ плоской монохроматической волны (12) , (13) сво-

Выполняя аналогичные действия применительно к закону Фарадея (11), последовательно получаем iu-— sin

— t

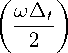
e -i? △ x / ² H y [ m ]

—i- — sin

— x

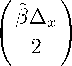
e     . ^д x / ² E q [ m ] ,

( 3л

— I E o  (22)

2       ⁰

и соответствующий импеданс в форме дится к

д _t ф = i — sin

ψ,

д х ф =

-i- — sin

— x

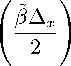
ψ.

и — _t

P        , л sin----

E 0 = - M — x     2

^H 0 “    ^— t ' в — x .

sin----- 2

Доказательство. Проверяется непосредственной подстановкой (12), (13) в (9) с учетом (6), (7). Выпишем здесь в явном виде только действие на ψ операторов сдвига (6), (7) при параметрах х,т = ± 2

Приравнивая правые части (20) и (23) и выполняя в получившемся равенстве перекрестное произведение сомножителей, получаем

sin ²

— 2 ц ^— x

sin ²

в — x

S ± ² ф = e ±i“ ^д t / ² ф,   S ± ² ф = e ^i^{e д} x / ² ф,   (16)

с помощью которых равенства (14) и (15) получаются эле-

ментарно.

Извлекая квадратный корень в последнем равенстве, окончательно приходим к (17), что и завершает доказательство.

Замечание 4 . Дисперсионное соотношение (17) метода FDTD существенно отличается от своего непрерывного аналога, имеющего вид [20, 21]

в = Ш ^ ЁД.

Вместе с тем отметим, что это отличие становится исчезающе малым при достаточно малой дискретизации пространства-времени. Действительно, сохраняя в рядах Тейлора разложения синуса при Л t и Л x ^ 0 только слагаемые первого порядка малости, из (17) легко получить

Л^

в = Шу/ЁД.

Подчеркнем, однако, что (26) справедливо только в пределе бесконечно малой дискретизации Л t , Л x ^ 0 . В общем же случае конечной дискретизации пространства-времени фазовые скорости волны в FDTD-сетке Йи с _р и в непрерывном пространстве с _р будут отличны.

Утверждение 2. Отклонение фазовой скорости волны в сетке Йи от соответствующего значения в непрерывном случае может быть описано равенством

Cоотношение (27) в рамках ограничений, рассматриваемых в настоящей статье (согласно которым исследуются недиспергирующие однородные среды, для которых и е _r и д _r — есть некоторые действительные константы), имеет очевидный смысл на следующей области определения параметров:

N _x е N \ 1 , е r ,д r ,S c е (0 , + ж ) с R , (34)

где ни множество натуральных чисел, больших единицы N \ 1 , ни множество положительных вещественных чисел считаются не содержащими непосредственно элемент + ж . Выход за рамки области определения (34) требует отдельного подробного исследования, и мы вернемся к нему в последнем разделе данной статьи.

Прежде чем перейти к обсуждению особенностей выражения (27) отметим, что диэлектрическая и магнитная проницаемости среды входят в него только в комбинации n r = Vе r Д r, (35)

Ср = ________Пу/ЁД______ р   Nx arcsin V rДr sin ( —c

^X L S _c      \N_X

где параметр N λ — есть число узлов пространственной сетки на длину волны в свободном пространстве

X = N x Л x .                 (28)

Доказательство. Используем связь фазовой скорости с волновым числом в непрерывном пространстве [20, 21]

и FDTD-сетке

ωω cp = в, cp = в,

что позволяет привести левую часть равенства (27) к виду

которая имеет физический смысл относительного показателя преломления среды.

Пример 1. Рассмотрим распространение плоской монохроматической волны с N x = 10 в стекле с показателем преломления n _r = 1 . 5 в случае числа Куранта S _c = 1 . Отношение (27) при этом равно с _р /с _р « 0 . 9777 , что в процентном отношении составляет численную ошибку примерно 2 . 23% . Таким образом, в данной ситуации на каждую единицу пути, равную длине волны, FDTD-расчет накапливает существенную фазовую ошибку порядка 8 . 03 ° . Заметим также, что улучшение дискретизации длины волны в два раза ( N _x = 20 ) сокращает соответствующие ошибки до значений 0 . 48% и 1 . 89 ° (т. е. примерно четырехкратно), как это и должно происходить для вычислительного метода второго порядка точности.

Ср   в

— = — = — cp

Далее применим (25) к числителю последнего равенства

c λ

2 п λ

ёДь ,

где длина волны в вакууме λ дискретизуется согласно (28),

что дает

в Л x

Пу/е _r д _r

N λ   ^.

Применяя теперь к знаменателю правой части (30) дисперсионное соотношение (17), в котором используются преобразования аналогичные (31), а также определение числа Куранта (1) совместно с (28), получаем

1.10

1.05

1.00

0.95

0.85

0.80

0.75

0.70

2     4     6     8    10    12    14    16    18    20

N λ

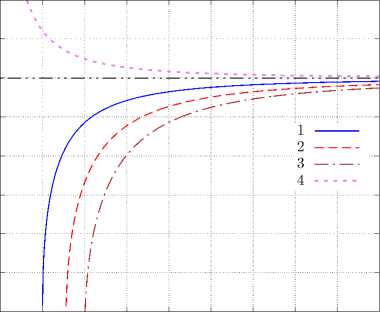
Рисунок 3. Зависимость фазовой скорости, определяемой согласно методу FDTD по отношению к ее точному значению (27), от параметра дискретизации длины волны N λ для некоторых сред с относительными показателями преломления n _r . Число Куранта S c = 1 .

Figure 3. Dependence of the phase velocity ratio, determined according to the FDTD method with respect to its exact value (27), on the wavelength discretization parameter N λ for some media with relative refractive indices n r . The Courant number S c = 1 .

в Л X   „

----= arcsin

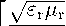
c

sin

nS c

N λ

Подстановка двух последних равенств в (30) приводит к результату (27), что завершает доказательство.

Особенности численной дисперсии метода FDTD, определяемые выражением (27), и дополняющие приведенный выше пример, представлены на рис. 3, где показано семейство кривых, для которых n r > S c (а именно, n r = д/2 для кривой 1 , n r = V3 — для линии 2 и n r = 2 — для 3 соответственно). Видно, что увеличение показателя преломления среды при плохой дискретизации длины волны приводит к существенному запаздыванию волны, моделируемой методом FDTD, что выражается в значительном отклонении отношения c p /с p от единицы.

Кроме того, на рис. 3 изображена кривая 4 , отвечающая случаю n r < S _c ( в да нном конкретном случае выбрано значение n r = у/ 1 / 2 ). Этот пример демонстрирует, что в средах оптически менее плотных, чем вакуум, FDTD-расчет приводит к распространению моделируемых волн с опережением по сравнению с истинной скоростью.

Следствие 1. Из рис. 3 видно, что точность FDTD-расчета падает с уменьшением N _x , а кроме того — по мере отклонения проницаемости среды от единицы (что имеет место и в диэлектриках, и в магнетиках, и в магнитных диэлектриках).

Следствие 2. Легко вычислить предел отношения (27), который независимо от величин nr и Sc равен lim cp = 1. (36)

N X ^ + ^ c p

Это означает, что точность FDTD-расчета улучшается с ростом N _x .

Замечание 5 . Ухудшение точности FDTD-расчета в среде с n _r >  1 связано с тем, что длина волны в такой среде короче, чем в вакууме, и малой дискретизации длины волны N _x оказывается недостаточно для корректного расчета. Однако простой перенос этого утверждения на случай среды с е _r <  1 не так очевиден и требует уточнения.

Следствие 3. Кроме того, рис. 3 указывает на то, что высокочастотные компоненты волнового пакета в средах с е _r >  1 имеют тенденцию к запаздыванию, в то время как в средах с е _r <  1 эта особенность меняется на противоположную — высокочастотные компоненты волнового пакета в сетке Йи распространяются с большей фазовой скоростью, чем это имеет место в действительности. Другими словами, в средах оптически более плотных, по сравнению с вакуумом, FDTD-расчет приводит к возникновению численной дисперсии, имеющей характер аномальной дисперсии [26]. И наоборот, — при моделировании оптически менее плотных сред, влияние FDTD-дискретизации соответствует поведению нормальной дисперсии (при этом «красные» компоненты волнового пакета «обгоняют синие»).

Замечание 6 . Структура знаменателя (27) имеет явное сходство с формой дисперсионных уравнений, получаемых в задачах о распространении волн в средах с периодическими неоднородностями [19,27–29].Аименно, — здесь фигурирует функция

ф(Nx ,Sc ,nг) = nr sin ^Sc, (37) Sc Nx характер которой определяет полосы пропускания и не- пропускания сетки Йи. Действительно, легко понять, что область значений параметров (Nx, Sc, nr), на которой выполняется условие |ф(Nx,Sc,nr)| > 1, отвечает непро-пусканию волн, так как выражение arcsin ф при этом не имеет смысла в вещественных значениях.

Подобная картина явления имеет место в модели Кро-нига-Пенни, а также в уравнениях Хилла и Матье, описывающих параметрические колебания [19, 27–29], а также распространение волн в системах с пространственной периодичностью в расположении неоднородностей. В качестве периодической структуры в нашем случае (в методе FDTD) выступает непосредственно сама расчетная сетка Йи. При этом пропускание и непропускание волн (квантово-механический аналог — разрешенные и запрещенные зоны) определяется как раз величинами N _x , S _c и n _r .

S c

-1

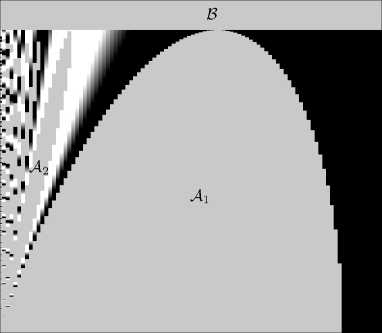
50    100    150    200    250    300    350

N λ

( N _x ,S _c ) -диаграмма полос пропускания сетки Йи

Рисунок 4.

при n r = 100 .

Figure 4. ( N _x ,S _c ) -diagram of Yee grid bandwidths when n _r = 100 .

Рисунок 4 иллюстрирует ( N _x ,S _c ) -диаграмму полос пропускания сетки Йи, построенную на основе функции (37) для сравнительно большого значения показателя преломления среды n _r = 100 . Области полос непропускания {A i } _i ^N ₌₁ , соответствующие условию | ф ( N _x ,S _c ,n _r ) I >  1 , изображены на этой диаграмме однотонной заливкой серого цвета. Общее число таких областей N (на рис. 4 отмечены первые две из них) зависит от величины показателя преломления среды n r и растет с увеличением последнего. Полосы пропускания представлены на данной диаграмме градиентной заливкой, меняющейся от черного ( ф = +1 ) к белому ( ф = — 1 ) цвету. Именно в рамках последних областей имеет смысл дисперсионное соотношение в форме (27).

Также на рис. 4 серым цветом выделена область B , определяемая неравенством S _c > n _c , в рамках которой метод FDTD также не может обеспечивать корректного численного решения задачи о распространении волны в однородной недиспергирующей среде. Аргументы, поддтвер-ждающие справедливость данного утверждения, приведены в следующем разделе статьи при обсуждении рис. 6.

• 3.    Связь численной дисперсии с числом Куранта

Теперь, после проведенного предварительного исследования, обсудим алгоритм коррекции численной диспер- сии с помощью специального выбора числа Куранта. Его возможность опирается на соотношение (27), из которого непосредственно вытекает следующий результат.

Утверждение 3. При любых заданных ε r и µ r , принадлежащих области определения (34) , всегда можно устранить вычислительные ошибки, связанные с численной дисперсией, задавая число Куранта равным

S c = V ^£ r M r ■

Доказательство. Проверяется непосредственной подста- новкой (38) в (27).

□

Замечание 7 . Значение числа Куранта (38) можно назвать «магическим», так как в этом случае фазовая скорость волны в FDTD-сетке c p точно совпадает с реальным значением фазовой скорости c p , независимо от выбранной дискретизации длины волны N λ . В то же время в источнике [14] «магическим» называется значение S _c = 1 , что справедливо только для вакуума, но никак не в общем случае. Здесь же отметим, что наш выбор (38) эквивалентен заданию S _c = 1 , используемому в книге [17].

Несколько примеров, иллюстрирующих идею применения «магического» числа Куранта (38) для коррекции программной дисперсии в недиспергирующих однородных средах, ограниченных выбором параметров (34), приведены на рис. 5.

1.0

E z [m] 0.5

0.0

q= 130, n r = 1.0 q = 80, n r = 2.0

q = 155, n r ≈ 0.7

/

P 5          P 1    P 6

0    25    50    75   100   125   150   175   200

m

1.0

J ^q 0.5

0.0

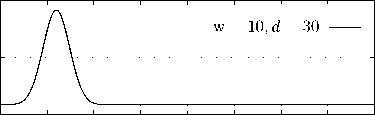
0    25    50    75   100   125   150   175   200

q

Рисунок 5. Моделирование распространения импульсов гаус сов а вида в средах, оптически более P 5 ( n _r = 2 ) и менее P 6 ( n _r = у/ 1 / 2 ) плотных, чем вакуум, с применением коррекции программной дисперсии (38). Figure 5. Simulating of Gaussian pulse propag atio n in media optically more P 5 ( n _r = 2 ) and less dense P 6 ( n _r = у/ 1 / 2 ) than vacuum, using correction of numeric dispersion (38).

Рисунок 5 подтверждает идею, сформулированную в виде Утверждения 3 — численная дисперсия здесь действительно не имеет места ни в случае среды оптически более плотной по сравнению с вакуумом (импульс P5), ни в случае оптически менее плотной среды (импульс P6). Рисунок 5 следует сопоставить с рис. 1, на котором численная дисперсия отчетливо проявляется на форме импульса P2. Замечание 8. Отметим также, что распространение электромагнитного поля в пространстве со временем (определяемым, как и всегда, величиной дискретного индекса q), представленное на рис. 5 для импульса P5, происходит с видимым опережением аналогичного процесса для импульса P2 на рис. 1 в два раза. Следует подчеркнуть, что это опережение — только кажущееся, так как его причиной является именно двукратное отличие в числах Куранта, выбранных в случае рис. 1 и 5. В действительности же (при учете поправки на Sc), все временны́ е характристи-ки сигналов на рис. 1 и 5 идентичны. Другими словами, если считать пространственный шаг решетки Ax фиксированным параметром, не меняющимся при переходе от моделирования в случае Sc = 1, представленного на рис. 1, к моделированию с числом Куранта (38), то «цена» каждого временного шага At (а вместе с ним, и полная продолжительность моделирования) изменится в √εrµr раз. Тот же эффект (с точностью до замены слов «опережение» на «запаздывание») имеет место и в случае оптически менее плотных сред (см. импульс P6) на рис. 5.

Замечание 9 . Также отдельно укажем на то, что моделирование распространения импульса P ₆ в среде оптически менее плотной, чем вакуум, в соответствии с расчетным алгоритмом (2) - (5) при выборе числа Куранта S _c = 1 принципиально невозможно. Несложно убедиться в том, что вычисления в этом случае очень быстро приводят к расходимостям, не давая никакой полезной информации, и принципиально не описывают данный частный случай.

Последнее замечание прекрасно иллюстрирует рис. 6, на котором показан лавинообразный процесс накопления численных ошибок в процессе расчета по алгориму (2)– (5) в случае превышения числа Куранта S _c , по сравнению с n _r , всего на 0 ■ 1% . Данная иллюстрация построена при тех же параметрах источника сигнала J ^q , что и на рис. 1 и 5, для случая вакуума, хотя принципиально такая же картина имеет место и в случае любых других однородных недиспергирующих сред из области определения (34).

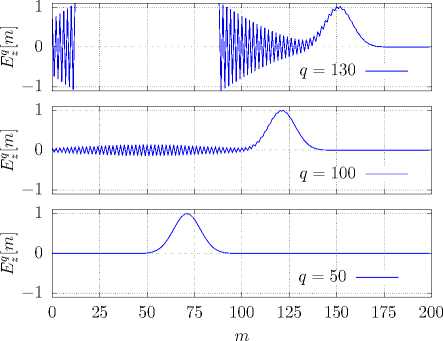
Рисунок 6. Временная динамика разрушения численного решения, получаемого в процессе вычислений согласно алгоритму (2) – (5) при S c — n r = 10 - 3 .

Figure 6. Time dynamics of the numerical solution destruction obtained during computation according to the algorithm (2) – (5) when S c — n r = 10 - 3 .

Как видно из рис. 6, к моменту времени q = 130 уровень шума, произвольно возникающего в результате вычислений по схеме (2) - (5) при Sc — nr = 10-3, двухкратно превышает величину полезного сигнала по абсолютному значению. При этом пространственная протяженность части сетки Йи, затронутой данным шумом, составляет 3/4 от всей длины расчетной области. Последнее обстоятельство существенно искажает форму заднего фронта моделируемого полезного сигнала. Далее с последующим развитием процесса при q > 130 полезное решение разрушается полностью.

Дополнительные численные эксперименты, выполненные нами, также показывают, что эффекты, связанные с накоплением ошибок, вследствие самовозбуждения сетки, имеют место всегда при выполнении неравенства S c > n r . Так, при S с — n r = 10 - ⁴ самовозбуждение сетки становится заметным уже после прохождения полезного сигнала, однако его лавинообразный характер наблюдается и в этом случае. Все эти наблюдения можно обобщить в форме следующего утверждения.

Утверждение 4. Расчетный алгоритм (2) – (5) быстро расходится и не может быть использован для получения корректного численного решения задачи о распространении сигналов в недиспергирующих однородных средах при выборе S _с > n r .

Доказательство. Исчерпывающая аргументация справедливости данного утверждения на «физическом уровне строгости» приведена выше при обсуждении рис. 6.

Применением данного утверждения как раз и обясня-ется наличие области B , показанной на рис. 4, хотя с формальной точки зрения функция (37) при этом не превышает единицу по модулю.

Замечание 10 . В то же время отметим, что выбор значений S _с <  n n , согласованный с условием | ф ( N x ,S _с ,n _r ) | <  1 , не приводит к столь драматическим последствиям, которые имеют место в Утверждении 4.

Важным следствием проведенного таким образом подробного исследования, основные результаты которого сдержатся в Утверждениях 3 и 4, является еще один факт. Следствие 4. Задание числа Куранта в форме (38) — единственно возможный оптимальный выбор с точки зрения применения численного FDTD-алгоритма (2) – (5) для моделирования распространения сигналов в недиспергирующих однородных средах.

Доказательство. Оптимальность такого выбора обусловлена тем, что он устраняет численную дисперсию при моделировании сигналов любой формы и спектрального состава, не противоречащих Утверждению 2 работы [18], распространяющихся в широком классе недиспергирующих однородных сред, описываемых областью определения (34). Единственность вытекает из Утверждения 4.

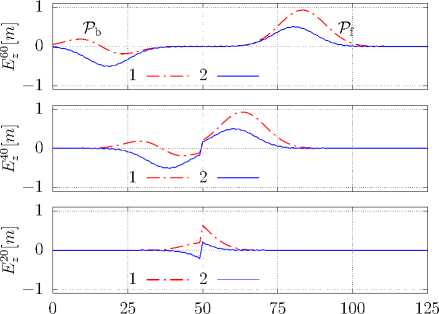
Замечание 11. Проблема, оставшаяся нерешенной до конца на данный момент (возникающая при внимательном изучении применения алгоритма (2) – (5) к однородным недиспергирующим средам, оптически отличным от вакуума), состоит в том, что в данном случае помимо основного сигнала с избранной направленностью всегда наблюдается сигнал сравнительно малой амплитуды обратной направленности. Назовем для краткости этот последний сигнал — обратным Pb, в противоположность исходному — прямому Pf. Иллюстрация этой проблемы приведена на рис. 7, который построен при тех же параметрах источника сигнала, что и рис. 1 и 5.

Рисунок 7 демонстрирует формирование обратного импульса P b при моделировании распространения сигнала гауссовой формы в средах, оптически менее плотных, чем вакуум при оптимальном выборе числа Куранта. Видно, что характер этого явления существенно зависит от величины относительного показателя преломления n _r среды. При стремлении последнего к нулю этим явлением уже нельзя пренебречь, так как оно приводит к искажению характеристик и полезного прямого сигнала P _f . В то же время, в случае n _r >  10 - ¹ соответствующая численная ошибка сравнительно мала, и может быть оценена не превышающей уровня в 1% .

m

Рисунок 7. Динамика формирования прямого P f и обратного P b импульсов при моделировании распространения сигнала гауссовой формы в средах, оптически менее плотных, чем вакуум при оптимальном выборе числа Куранта. Штрих-пунктирная кривая 1 соответствует случаю S c = n _r = 10 - 1 , сплошная линия 2 — S c = n _r = 10 - 2 .

Figure 7. Dynamics of forward P f and backward P b impulses formed in simulating the propagation of a Gaussian-shaped signal in media optically less dense than vacuum under optimal choice of the Courant number. The dashed-dotted curve 1 corresponds to the case of S _c = n _r = 10 - 1 , the solid line 2 — S c = n _r = 10 - 2 .

• 4.    Границы применимости основных результатов

В завершении данной работы обсудим вопрос о применимости полученных здесь результатов за рамками области определения (34).

Во-первых, укажем на то, что интервал значений 0 < e _r , ц _r <  1 , входящий в область определения (34), используемый при выполнений условий Утверждения 3, уже сам по себе расширяет диапазон применимости развитого в данной работе расчетного алгоритма на область экзотических сред, обычно не рассматриваемых в литературе.

Во-вторых, отметим, что наш численный алгоритм (2) – (5) остается справедливым и при расширении области опредления (34) на интервал e _r ,ц _r е ( —ж , + ж ) при условии одновременной отрицательности проницаемостей среды e _r ^ _r >  0 .

Среды с одновременно отрицательными проницаемо-стями, как известно [23–25], называются левыми. В таких средах могут распространяться обратные волны [30], определяемые тем фактом, что для них скалярное произведение волнового вектора k (в нашей работе всюду k = в e x )

и вектора Умова-Пойнтинга S — отрицательно

( k • S ) <  0 ,                     (39)

где поток энергии, переносимый волной, и определяемый вектором S , равен [20–23, 26]

S = C [ E x H ] .             (40)

4 n

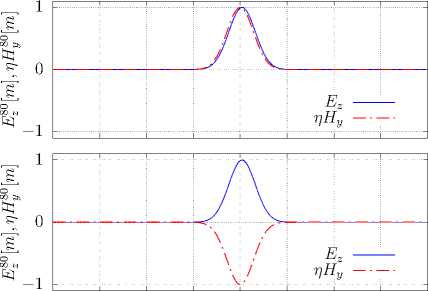
Справедливость такого обобщения демонстрирует рис. 8, на котором представлены результаты сравнения волновых пакетов, формируемых тем же источником сигнала, что и на рис. 1, 5 – 7, зафиксированные в одинаковый момент времени q = 100 , при распространении в правой среде с е r = ц r = +1 (нижняя половина рисунка) и левой среде с е r = ц r = — 1 (верхняя половина).

0    25    50    75   100   125   150   175   200

m

Рисунок 8. Мгновенные снимки прямых (нижняя половина) и обратных (верхняя часть) волн, распространяющихся в сетке Йи согласно расчетному алгоритму (2) – (5).

Figure 8. Instantaneous snapshots of forward (bottom half) and backward (top half) waves propagating in the Yee grid according to the computational algorithm (2) – (5).

Легко убедиться в том, что для волнового пакета, показанного в верхней части рис. 8 вектор Умова-Пойнтин-га (40) S f^ e x , что как раз и определяет обратную волну согласно условию (39).

И наконец, поясним, что справедливость алгоритма (2) – (5) при расширении области опредления (34) на интервал е r ,ц r G ( —ж , + ж ) при условии неодновременной отрицательности проницаемостей среды е r ц r <  0 в рамках данной работы нами не исследовалась. Это связано с тем, что при е r ц r <  0 постоянная распространения (25) оказывается мнимой величиной, что соответствует сильному затуханию волн в таких средах, которые вследствии этого оказываются сильно диспергирующими (для них распространение плоских волн оказывается невозможным, а вместе с этим теряет простой смысл Утверждение 2, которое требует иной формулировки в данном случае). Все это выходит за рамки темы данной работы.