Влияние деформируемости угольного пласта на пространственное напряженно-деформированное состояние массива горных пород в окрестности полости
Автор: Хапилова Нелли Сергеевна, Залетов Владислав Всеволодович, Залетов Сергей Владиславович
Журнал: Горные науки и технологии @gornye-nauki-tekhnologii
Статья в выпуске: 1, 2014 года.
Бесплатный доступ
Предложен метод расчета пространственного напряженно- деформированного состояния массива горных пород в окрестности призматической выработки с произвольной формой сечения в плане. Численно исследовано распределение напряжений вблизи полости в форме прямоугольного параллелепипеда.
Массив горных пород, угольный пласт, призматическая выработка, пространственное напряженно-деформированное состояние, закономерности
Короткий адрес: https://sciup.org/140215824
IDR: 140215824 | УДК: 539.3:
Текст научной статьи Влияние деформируемости угольного пласта на пространственное напряженно-деформированное состояние массива горных пород в окрестности полости
Разработка и оптимизация способов охраны подземных выработок и предупреждения динамических явлений в шахтах, как правило, базируются на теоретических либо экспериментальных исследованиях закономерностей распределения напряжений в окрестности полостей, образованных в массиве горных пород. Ниже на основе аналитического решения задачи о пространственном напряженно-деформированном состоянии массива с выработкой, проведенной в пласте полезного ископаемого, проанализированы закономерности распределения напряжений в горных породах, вмещающих угольный пласт с полостью в форме прямоугольного параллелепипеда.
Обозначим через 2 h мощность горизонтального угольного пласта, залегающего на глубине H от дневной поверхности.
Введем декартову прямоугольную систему координат, совместив координатную плоскость x,y с поверхностью контакта пласта полезного ископаемого с породами, ось z направим вертикально вверх (рис. 1).
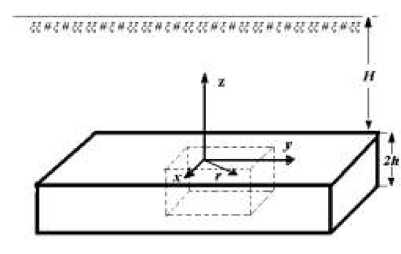
Рис. 1. Схема угольного пласта с призматической выработкой.
Пространственное напряженное состояние ненарушенного массива опишем формулами
G x 0 = ст y 0 =a. g ( H z ), ° z 0 g ( H z ), т x 0 y = т xz = т yz 0 (1)
Здесь О0, 0,..., 0 – компоненты тензора нормальных и касательных напряжений, α – коэффициент бокового распора, ρ - средняя плотность горных пород, g - ускорение силы тяжести.
В массиве с выработкой неизвестные напряжения оe, e,..., e представим в виде сумм e0
x= Gx + О"x, оy= Gy+ оy, e0
аz— Gz + О"z, о xy - тxy + тxy, e0 e0
xz xz xz , yz yz yz .
где О , О ,..., 7" - дополнительные напряжения, появление которых связано с созданием полостей в массиве.
Для достаточно больших глубин залегания разрабатываемого пласта при определении дополнительных напряжений можно пренебречь влиянием дневной поверхности. Тогда задача о напряженном состоянии массива с горизонтальным угольным пластом может быть рассмотрена как трехмерная задача теории упругости для полупространства, лежащего на перфорированном упругом основании, моделирующим пласт полезного ископаемого с выработками.
Считаем, что в плане сечение V призматической выработки имеет произвольную форму. Сформулируем граничные условия смешанной задачи. При z = 0 в области V , являющейся потолком выработки, в случае отсутствия крепи дополнительное напряжение ^, согласно (1), (2), равно
ρgH. Касательные напряжения xz в точках граничной плоскости равны нулю. Чтобы учесть деформируемость пласта, принимаем, что в точках поверхности контакта угля с породами выполняется условие пропорциональности нормальных напряжений и смещений.
В работе [1] построено решение сформулированной смешанной задачи теории упругости для изотропного полупространства, позволяющее рассчитать опорное давление на угольный пласт, другими словами, определить распределение нормального напряжения σ ze в плоскости контакта угля с породами. Численные результаты исследования пространственного опорного движения в концевой части (нише) очистной выработки приведены в книге [2]. Ниже кратко изложим один из способов решения смешанной задачи, позволяющий вычислить компоненты тензора напряжений не только в плоскости контакта угля с породами, но и в произвольных точках массива.
Для построения искомого решения смешанной задачи используем аналитическое решение задачи о действии сосредоточенной силы на полупространство, лежащее на упругом основании [3]. В этом случае задача осесимметрична, поэтому введем цилиндрическую систему координат r , о , z . В результате решения задачи с помощью интегрального преобразования Ханкеля для компонент напряжений, действующих в изотропном полупространстве, лежащем на упругом основании, имеем следующие формулы [4], [5]:
P 12 V
2 тс 2
z
r 2
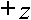
3 r z 2
r 2 z 2 2
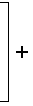
P 1 2 V
2 тс
z 1
32 r 2 z 2 2 r
r 2
z
т rz
3Pr z 2
2 к r 2 z 2 52
PXz т t 2 e — #Г dt.
rt t .
2 IT t V 1
2 0 t
Здесь P – сосредоточенная силa, J 0 (rt), J 1 (rt) – функции Бесселя 1
нулевого и первого порядка, r x2 + y2 2 . Постоянная χ определяется из соотношения z =2k1 v- 2 , (7)
E где v – коэффициент Пуассона, Е – модуль упругости пород, k – «коэффициент постели» упругого основания, характеризующий деформируемость угля.
Приравнивая в формуле (5) координату z нулю, получаем закон распределения нормального напряжения на границе полупространства
PУ ^ - dt
СУ z P -J t J 0 rt dt PG ( x , y )
2 71 00 t +z
При единичной сосредоточенной силе равенство (8) совпадает с аналогичной формулой для σ z , приведенной в работе [1]. Закономерности распределения напряжений и перемещений в изотропном полупространстве, лежащем на упругом основании, при действии на него сосредоточенной силы исследованы в [4], [5].
При переходе в решении (3)-(6) от цилиндрической к прямоугольной системе координат вычислим напряжения от единичной сосредоточенной силы, приложенной в произвольной точке ( ξ,η ) области V . Составляющие напряжений в декартовой системе координат x,y,z имеют вид [6]:
<7 x
(<т r * СУ e )+( ст r )
x 2 y 2
x 2 y 2
аy
( (У r +<У0 )
( (Т r - не )
x 2 y 2
x-^ 2 y 2
c
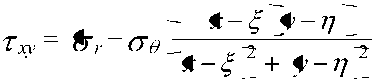
xz
rz
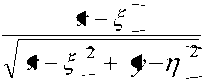
yz
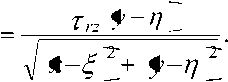
Здесь напряжения , , c , задаются соотношениями (3)-(6), в которых величина полагается равной r x 2 y 2 12 .
Переход от сосредоточенной силы к распределенной нагрузке осуществим общепринятым в теории упругости способом с помощью принципа суперпозиции. Выделим в окрестности точки приложения сосредоточенной силы (^,п) элементарную площадку d^dq и проинтегрируем, используя [7],[8], правые части соответствующим образом преобразованных соотношений (9)-(14) по области приложения распределенной нагрузки неизвестной интенсивности в(^/ц).
В результате получаем аналитические формулы для расчета напряжений в произвольных точках полупространства
x ( x , y , z ) 1 ( , )
2 V
3 z ( x )2
1 2 z ( y )2 ( x )2 ( y )2
(1 2 tz ) J 0 ( t )
( x )2 ( y )2
(1 2 tz ) J 1( t ) e
1z tz tdt t
dd ,
оо
z ( x , y , z ) 1 ( , ) 3 z (1 tz ) J 0( t ) e
2 V 1 1 5 0
tz tdt
d d (15)
z
3 P z 3
2 r 2 z 2 5 2
P t 1+ tz — т
J 0 rt e tz dt ,
2 тс 0 t 0
в котором функция G определяется равенством (8). При переходе к безразмерным напряжениям левые и правые части соотношений (15), (16) делятся на pgH.
Результаты численных исследований распределения напряжения для прямоугольной области V со сторонами 10 м и 6 м приведены на рис. 2, 3. Начало декартовой системы координат совмещено с точкой пересечения диагоналей прямоугольника. Так как область V симметрична относительно координатных осей x,y то пространственное распределение безразмерных нормальных напряжений 5^=0^/ pgH , crz Hozl pgH в плоскости z=6 (рис. 2a, 3a ) исследовано в области V = { x е[0;10], у е[0,10]} , а в плоскости z=0 (рис. 2b,3b ) в области V = { x е[5;10], у е[3,10]}, которая является поверхностью контакта угольного пласта с породой. При расчетах коэффициент Пуассона пород полагался равным 0.25.
Входящий в равенстве (7) коэффициент к оценивался по известной формуле [2]
к= (1- г с ) Ес h (1 + Г с )(1-2г с ) где vc, Ес - коэффициент Пуассона и модуль Юнга угольного пласта.
Трехмерные графики построены при х=1м 1 . Аналогичные графики строились для всех компонент напряжений при варьировании параметра %.
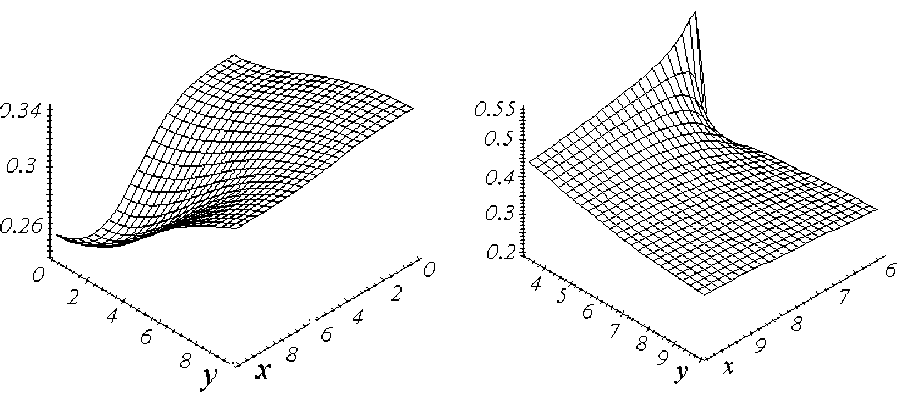
а) Область V 1 , плоскость z=6
b) Область V2, плоскость z=0
Рис. 2. Распределение безразмерных напряжений ах
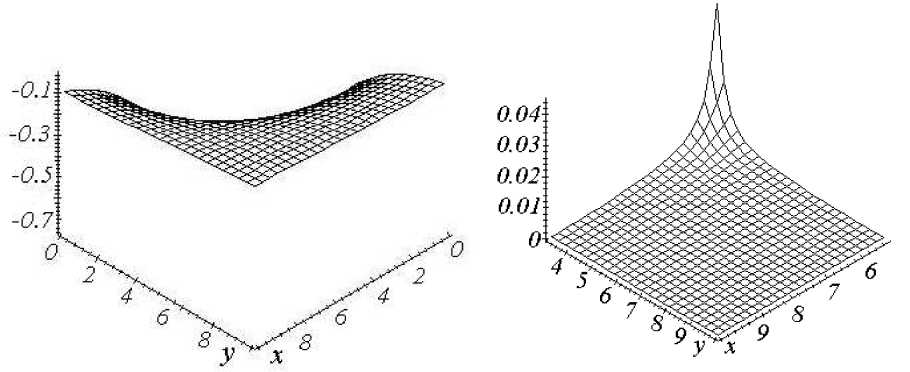
a) Область V 1 , плоскость z=6
b) Область V 2 , плоскость z=0
Рис. 3. Распределение безразмерных напряжений сz
Из рис. 2, 3 видно, что картины распределения напряжений в плоскостях z=6м и z=0 отличаются качественно. Расчеты показывают, что в плоскости z=6м в некоторой области V3 , находящейся непосредственно над областью V, распределение напряжений зависит в основном от нагрузки ρgH, по мере удаления от области V3 в плоскости z=6м усиливается влияние параметра χ, характеризующего деформируемость угольного пласта. Зависимость распределения напряжений от параметра χ также возрастает при приближении к граничной плоскости. Из расчетов следует, что в плоскостях z=const нормальные напряжения с ростом χ от 0.2 At 1 до 1 Ai 1 увеличиваются в 2-4 раза, касательные изменяются на 2030%. Для получения полных напряжений в массиве необходимо к рассчитанным величинам ст , стy ,..., х прибавить начальные напряжения, которые задаются соотношениями (1).
массив горных пород, угольный пласт, призматическая выработка, пространственное напряженно-деформированное состояние, закономерности rock mass, coal seam, prismatic working, the spatial stressed-strained state, regularities t2dt
t
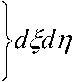
Список литературы Влияние деформируемости угольного пласта на пространственное напряженно-деформированное состояние массива горных пород в окрестности полости
- Кавлакан М.В., Михайлов А.М. Решение смешанной статической задачи теории упругости для полупространства на упругом основании//Докл. АН СССР, 1980. -Т.251, №6. -C. 1338-1341.
- Хапилова Н.С. Теория внезапного отжима угольного пласта. -Киев: Наукова думка, 1992. -232с.
- Залетов В.В. Осесимметричная задача теории упругости для изотропного полупространства, лежащего на упругом основании, при действии сосредоточенной силы//Труды Института прикладной математики и механики НАН Украины, 2004. -Т.9. -С.61-67.
- Залетов В.В. Распределение напряжений в изотропном полупространстве при заданных граничных условиях смешанного типа//107 Труды Института прикладной математики и механики НАН Украины, 2006. -Т.13. -С.83-91.
- Залетов В.В., Хапилова Н.С.//Труды Института прикладной математики и механики НАН Украины, 2010. -Т.20. -С.65-73.
- Амензаде Ю.А. Теория упругости.-М.: Высшая школа, 1971. -287 с.
- Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.-М.: Наука, 1974. -1108 с.
- Корн Г., Корн. Т. Справочник по математике. -М.: Наука, 1978. -832 с.


