Влияние диффузности ионосферы на оптимальную рабочую частоту декаметровой радиолинии

рассеянию радиоволн и изменению формы зондирующих радиосигналов. Соглаcно [4] диффуз-ность ионосферы обусловлена тем, что на п лав ное изменение по высоте ( h ) средней ЭК N ( h ) накладываются пространственные неоднородности ЭК A N ( h , р ), где р = ( х , у ). Поэтому диффуз-ность в слое F ионосферы наблюдается на высотно-частотной характеристике (ВЧХ) станции вертикального зондирования ионосферы (СВЗИ) в виде ее расплывчатости (утолщения) линии ВЧХ, которая возрастает по мере приближения частоты вертикального отражения ( f в ) волны к критической ( f _кр ). Уровень диффузности принято оценивать в баллах по 4-бальной шкале или по трем градациям уширения ВЧХ вблизи f .

В [5] обосновано, что уровень диффузности ионосферы целесообразно оценивать не в баллах, а по величине интенсивности ( β ) мелкомасштабных неоднородностей (ММН) ЭК ионосферы. Известна [6] методика определения в одно-скачковой ДКМ радиолинии оптимальной рабочей частоты (ОРЧ) по критерию максимального превышения сигнала над помехой в точке приема, при которой обеспечивается наибольшая надежность (вероятность) связи c достоверностью не хуже допустимой. Она разработана на основе учета зависимости глубины быстрых замираний в ДКМ радиолинии от выбора рабочей частоты (РЧ). При этом установлена зависимость параметра распределения глубины быстрых замираний ( m –параметра Накагами) от интенсивности ММН ионосферы ( β ). Однако в [6] не учитывалась возможность роста интенсивности ММН ионосферы ( β ) на порядок и, следовательно, существенного изменения ОРЧ относительно МПЧ и НПЧ в односкачковой ДКМ радиолинии в условиях диффузности ионосферы.

Интенсивности ММН ионосферы обычно [4-6] определяется как отношение в = о-AN (h)/N(h) величины среднеквадратического отклонения (СКО) флуктуаций ЭК AN(h, р)

в ММН ионосферы

Г--------2 т5

a a n ⁽ h ) = A N ( h , р )

к

среднему значению ЭК n(h) на некоторой высоте h . При этом на любой высоте ионосферы, вклю- чая высоту максимума ионизации h = hm, ин- тенсивность ММН остается неизменной: в = О an ( h )/N ( h ) = Oan ( hm )/N ( hm ) =const.

Способ определения интенсивности ММН ЭК в = O a n ( h m )/ Ж5 по результатам построения ВЧХ СВЗИ обоснован и реализован в патенте РФ [7]

Очевидно, что для достижения поставленной в статье цели необходимо установить зависимость изменения ОРЧ в односкачковой ДКМ радиолинии по мере возрастания интенсивности ММН ЭК ионосферы от обычных значений в = io ^{- 3} в нормальной среднеширотной ионосфере до в = 10 ^{- 2} в условиях ее возмущений типа диффузности [8].

Зависимость оптимальной рабочей частоты от диффузности ионосферы. Известно [3], что условием осуществления ДКМ связи с достоверностью и надежностью не хуже допустимых значений является превышение Р / Р > K2 c пн отношения мощности сигнала к мощности помех на входе приемника (ПРМ) над минимально необходимым значением. Это условие можно записать в виде E1 / E1 > T превышения отношения единичной напряженности поля сигнала к удельной напряженности поля помех в точке приема над техническим фактором (T ). Поскольку указанные напряженности (в отличие от технического фактора Т) зависят от выбора РЧ (f,), это условие можно записать в децибелах как

E С ( f , )/ E 1 ( f о ) - T >  0 ,              (1)

где T = K н K бз K мз V B /0,25 Р , G n D 2 .      (2)

Здесь K – наименьший необходимый кон эффициент защиты, определяемый видом работы; Kбз – коэффициент защиты от быстрых (интерференционных) замираний; Kмз – коэффициент защиты от медленных замираний; B – полоса пропускания приемника; Р - мощность передаваемого сигнала; G1 и П1 — коэффициент усиления и КПД фидера передающей антенны; D2 - коэффициент направленного действия приемной антенны. Отметим, что значение РЧ, при котором выполняется равенство

E С ( f , ) / E 1 ( f , ) - T = 0 согласно [2] соответствует НПЧ: f >  = f , .

Чтобы определить ОРЧ, следует учесть, что в ДКМ радиолинии коэффициент защиты от быстрых замираний (БЗ) K _бз должен зависеть от выбора РЧ ( f ₀ ), поскольку известно [1,2], что при выборе РЧ вблизи МПЧ возрастает рассеяние и глубина замираний принимаемого сигнала. Это согласно (2) обуславливает наличие частотной зависимости у технического фактора: K _бз ( f 0 ) ^u T ( f , ). Поэтому ОРЧ можно определить по критерию максимального превышения отношения сигнал/помеха E 1 ( f ₀)/ E П ( f 0 ) в точке приема над техническим фактором T ( f ₀) в результате решения уравнения

E 1 ( f о )/ E 1 ( f о ) - T ( f о ) = max , (3) где T ( f . ) = K н K бз ( f о ) K мз7 B /0,25 P , G , D 2 .

Известно [1, 3, 4, 6, 8], что обычно наблюдаемые в односкачковой ДКМ радиолинии райсовские или рэлеевские распределения быстрых замираний удовлетворительно аппроксимируются m -распределением Накагами в интервале 1 <  m < да . В этом случае коэффициент защиты от быстрых замираний K _бз можно определить как [1]

K бз = 2 m [ ( 2 Р ошдоп )^{- 1} m - 1 ]Д- 21п (2 Р ош_доп ) ] , ⁽⁵⁾

где P _{ош доп} - допустимое значение вероятности ошибочного приема сигналов. Анализ (5) показывает, что по мере увеличения глубины замираний (т.е. приближения m к значению 1, соответствующему релеевским замираниям) коэффициент защиты от них возрастает.

В свою очередь, параметр Накагами m в односкачковой ДКМ радиолинии полностью определяется дисперсией флуктуаций фазового фронта отраженной волны о ^ на выходе неоднородной ионосферы, величина которой зависит от используемой РЧ ( f , ) и уровня диффузности ионосферы ( в ) согласно выражениям [6]:

m = [1 - ехр( - 2 о 2 )] ^{- 1} , (6) ^где ° ф = ^{2 r}0L э [ n f о^{( h} д^{) в} c ^sec2 Ф о ] . ⁽⁷⁾

Здесь r₀ - наибольший размер ионосферных неоднородностей (м); L _э - эквивалентный однородный путь ДКМ волны в слое F ионосферы (м);

f ) ( h _д ) — рабочая частота ДКМ волны с действующей высотой h _д отражения от ионосферы (Гц); c - скорость света в вакууме (м/с); ф ₀ - угол падения волны на нижнюю границу отражающего слоя ионосферы; в — интенсивность ММН ЭК ионосферы.

На практике выбор РЧ ( f 0 ) в ДКМ радиолинии осуществляется на основе измерения действующей высоты отражения ( h _д ) вертикально направленной волны с частотой f в :

f)(h д) = fв(hд)sec фо, (8)

где секанс угла падения волны на нижнюю границу отражающего слоя вычисляется по заданной дальности связи (r) с учетом кривизны Земли (Rз $ 6370 км) как sec ф) « {1 + r2 / 4[hд (fв) + (r2 / 8R3 )]2 }0,5. (9)

Зависимость h _д ( f в ) действующей высоты отражения от частоты вертикальной волны обычно определяется по ВЧХ СВЗИ, а при параболической модели распределения ЭК в отражающем слое ионосферы ее можно рассчитать по формуле

(7,8) дисперсия флуктуаций фазового фронта с ф отраженной ДКМ волны на выходе неоднородной ионосферы прямо пропорционально зависит от значения РЧ ( f ₀ ( h _д ) = f в ( h _д )sec ф ₀ ) и интенсивности ММН ЭК ионосферы ( в ) и ее можно рассчитать по двум формулам:

с ф ( f 0 , в ) = 2 rL ,

n f 0 ( h д ) в "² c ^sec 2 ф 0

= 2 r L ,

^{n f}в ( h д ) ^{в 2} c sec ф ₀

h д ( f ) .

= ^h о ⁺

' z fв '

I ² f КР ^j

ln

( 1 + f в / f кр ) ( 1 - f в / f кр )

где h ₀ - нижняя граница слоя; z_m = h m - h ₀ -

высота максимума ионизации h_m относительно нижней границы h ₀ слоя; f кр = [ 80,8 N ( h m ) ] ^0,5 -критическая частота ионосферы.

Следует отметить, что используемый для вычисления с ф в (7) эквивалентный однородный путь ДКМ волны L , в слое F также зависит от

частоты вертикально направленной волны f в , отражающейся на высоте h _д , как

L , = [ ^h д ( f в ) - h о ]О +

кр

—

z м

f в

гх

^h д ^{( f}в ^{) — h} о ,

Ц 0,5

х j sec² Ф 0 - 0,5 1 +

кр

zм hд ( fв ) — h0

.

Методика определения ОРЧ односкач-ковой ДКМ радиолинии. Согласно выражениям

где sec ф ₀ и L , определяются согласно выражениям (9-11). Второе равенство (12) наглядно отражает физическую причину возрастания с ф ~ f _в ( h _д ) в по мере увеличения уровня диф-фузности ионосферы в = с _д N ( h )/ N ( h ) и частоты вертикально направленной волны f в с действующей высотой отражения h _д . Поскольку последняя близка к истинной высоте отражения волны h _д « h _от , то частота отражения вертикально направленной волны описывается выражением f в = [ 80,8 N ( h _от) ] . Поэтому произведение f _в в в (12) пропорционально величине СКО флуктуаций ЭК в ММН ионосферы с _{д N} ( h ) = N ( h ) в , которое возрастает по мере приближения h к высоте максимума ионизации h_m , где наблюдаются наибольшие средние значения ЭК N ( h m ) >  N ( h ) и их флуктуации с _М ( h m ) = N ( h m ) в >  с_ш ( h ) = N ( h ) в .

При повышении уровня диффузности ионосферы в произведение f в в ~ f ) в ~ N ( h )) в будет еще больше, что приведет к дальнейшему росту с ф .

Согласно выражениям (6, 7) параметр Накагами, характеризующий глубину замираний в односкачковой ДКМ радиолинии, через величину с ф (f ₀, в ) зависит от выбора РЧ ( f ₀ ) и уровня диффузности ионосферы ( в ):

m ( f„ в ) = { 1 - exp [- 2 сф ( f, в ) ] } - ' .(13)

Анализ выражений (12, 13) позволяет объяснить тот известный [1-4] факт, что при выборе в ДКМ радиолинии РЧ вблизи МПЧ

0,5

^f 0 ~ ^f м = ^{0,9 f} кр sec ф ) = 0,9 [ 80,8 N ⁽ h m ) ] sec ф ) произведение ^f 0 ( h д ) ^в ~ ^с возрастает и обуславливает рост с ф и уменьшение параметра m ( f 0 , в ) ~ 1/ сф ( f ₀ , в ) , т.е. увеличение глубины замираний принимаемых сигналов.

В свою очередь, параметр m ( f 0 , в ) согласно (5) определяет коэффициент защиты от быстрых замираний

K бз ( f ) , в ) =

2 m ( f о , в ) ( 2 Р ош доп ) — 1 m ^{( f 0 , в} ) - 1 [- 2ln ( ^{2 Р} ош доп ) ]

В соответствии с (14) выражение (4) для технического фактора односкачковой ДКМ радиолинии можно представить в следующем виде

T ( f , , в ) = К н К бз ( f о , в ) K мз V B /0,25 Р , G , D 2 =

= Kбз ( f) , в ) Тмз, где Tнмз = КнКмз ^B /0,25Р, G,D2 - составляющая технического фактора T(f0, в), не зависящая от выбора РЧ и диффузности ионосферы.

На основе (15) можно при заданном уровне диффузности ионосферы ( в ) определить ОРЧ как частоту ( f ₀ = f _орч ), на которой обеспечивается максимальное превышение отношения сиг-нал/помеха E _c¹( f ₀)/ E _п¹( f ₀) в точке приема над техническим фактором (15) T ( f 0 , в ) в результате решения уравнения (3):

E 1 ( f о )/ E 1 ( f о ) — T ( f о , в ) = max .   (16)

Приведем пример определения ОРЧ одно-скачковой ДКМ радиолинии на основе расчета зависимости T ( f ₀ ) технического фактора от выбора РЧ согласно (15) при фиксированном уровне диффузности ионосферы в = const . Для определения согласно (12) величины о ф 2 (f 0 , в ) необходимо предварительно рассчитать h _д( f _в) и sec ф ₀ по формулам (10), (9). Приведенные ниже примеры расчета h _д ( f в ) и sec ф ₀ произведены при следующих исходных данных: h 0 = 2,5 - 10 5 м, z м = ¹⁰5 м, ^f кр = 4 МГц, f в/ f ср = 0,1...0,9 , r = 2000 км, R _з » 6370 км. Далее по формулам (11) и (8) проведены расчеты эквивалентного однородного пути ДКМ волны в слое F ионосферы L _э и рабочей частоты ДКМ волны f ₀ ( h _д ) с действующей высотой h _д отражения от ионосферы. На этой базе при заданных значениях r ₀ = 5 • 10² м, c = 3 - 10 8 м/с и типовой интенсивности неоднородностей среднеширотной ионосферы в = 5 - 10 — ³ произведен расчет согласно (12) величины с ф (f , , в ) . Далее в соответствии с выражениями (13, 14) производится расчет параметра m ( f , , в )~^ °"ф (f 0 , в ) и коэффициента К _бз ( ^f , , ^{в )} при р _ош д_оп = 3 - 10 ^{- 3} . Расчет T ( f ₀) по формуле (15) проведен при значениях К _н « 10 дБ, К _мз ~ 11 дБ, B = 0,3 кГц, Р 1 = 1 кВт, G 1 = 3 , D 2 = 2 . Полученная частотная зависимость T ( f 0 , в ) при в = 5 - 10 ^{- 3} представлена на рис. 1 штрихпунктирной линией.

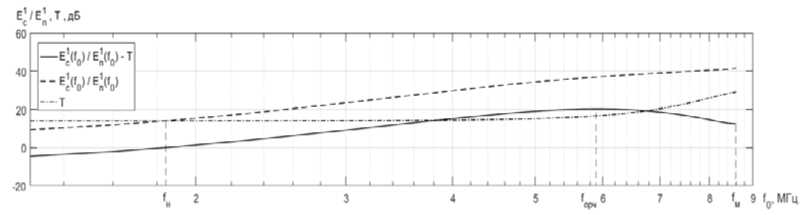
Рис. 1. Результаты вычисления оптимальной рабочей, максимально и наименьшей применимой частот в односкачковой декаметровой радиолинии при интенсивности неоднородностей ионосферы в = 5 • 10 ^{- 3} .

Здесь же пунктирной линией представлена типовая [3, 6] частотная зависимость E _c¹( f ₀)/ E _п¹( f ₀) и пунктирной линией - разность

E 1 ( f 0 )/ E 1 ( f ) ) — T ( f ) ) для диапазона рабочих частот от f ₀ =1 МГц до МПЧ ( f _м ). Эти зависимости при традиционно определяемой МПЧ

( f м = 0,9 f кр sec ф ₀ - 8,6 МГц) позволяют по точке пересечения графиков E С ( f ₀)/ E 1 ( f ₀) и T ( f ₀) найти значение НПЧ ( f н - 1,9 МГц) и по точке достижения максимума функции (16) их разности E 1 ( f о )/ E П ( f о ) - T ( f о , в ) = max определить значение ОРЧ ( f орч - 5,9 МГц).

Полученные результаты позволяют разработать методику определения ОРЧ односкачко-вой ДКМ радиолинии по критерию обеспечения максимального превышения отношения сиг-нал/помеха, которая сводится к следующим этапам:

• 1.    Расчет дисперсии флуктуаций фазового фронта о ^ (f ₀, в ) отраженной ДКМ волны на выходе неоднородной ионосферы в зависимости от значений РЧ ( f ₀) и интенсивности ММН ЭК ионосферы ( в ) в соответствии с выражениями (7-12).

• 2.    Расчет параметра Накагами m ( f ₀, в ) ~ 1/ ^ ( f ₀, в ) , характеризующего глубину замираний в односкачковой ДКМ радиолинии, согласно выражению (13).

• 3.    Расчет коэффициента защиты от быстрых замираний в односкачковой ДКМ радиолинии согласно функциональной зависимости (14) к бз ( f о , в ) = ^ [ m ( f 0 , в ) ] .

• 4.    Расчет технического фактора односкачко-вой ДКМ радиолинии согласно произведению (15) T ( f„ в ) = K бз ( f , , в ) ■ T m3 .

• 5.    Определение частотной зависимости отношения E 1 ( f , )/ E 1 ( f ₀) единичной напряженности поля сигнала E 1 ( f ₀) к удельной напряженности поля помех E 1 ( f ₀) в точке приема.

• 6.    Определение рабочей частоты ( f ₀ = f _орч ), на которой обеспечивается максимальное превышение отношения сигнал/помеха E 1 ( f ₀)/ E П ( f ₀) над техническим фактором T ( f ₀, в ) при заданном уровне диффузности ионосферы ( β ), на основе решения уравнения (16) E 1 ( f 0 )/ E 1 ( f 0 ) — T ( f 0 , в ) = max.

Анализ влияния диффузности ионосферы на ОРЧ односкачковой ДКМ радиолинии. Покажем, что выбор ОРЧ в односкачковой ДКМ радиолинии существенно зависит от интенсивности ММН ЭК ионосферы, которая в средних широтах может изменяться в широких пределах [8]: от в = 10 ^{- 3} до 10^-2. Результаты вычисления разности E _c / E _п ( f ₀) - T ( f ₀) по приведенной выше методике определения ОРЧ для граничных значений интенсивности ММН ЭК в = 10 ^{- 3} и 10 ^{- 2} (а также в = 5 ■ 10 ^{- 3} ) представлены на рис. 2.

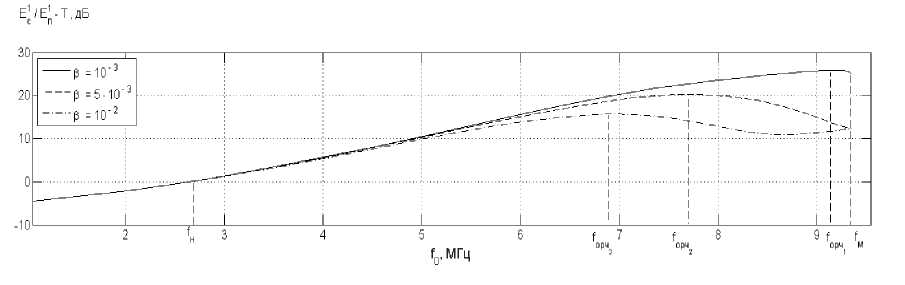
Рис. 2. Результаты вычисления оптимальной рабочей частоты ДКМ радиолинии при трех значениях интенсивности неоднородностей ионосферы: в = 10 ^{- 3}; 5 ■Ю ^{- 3}; 10 ^{- 2}

Из рис. 2 видно, что при увеличении интенсивности ММН ЭК ионосферы ( в = 10 ^{- 3}...10 ^{- 2} ) значения НПЧ и МПЧ не изменяются ( f м - 8,6 МГц, f _н ® 1,9 МГц), тогда как оптимальная рабочая частота (при которой достигается наилучшая надежность ДКМ радиосвязи) понижается ( f ,рч1 - 8,2 МГц; f орч 2 - 5,9 МГц; f _фч з - 4,9 МГц).

Аналогично рис. 2 по разработанной методике можно построить более детальные графики зависимостей ОРЧ от интенсивности ММН ЭК ионосферы. На их основе можно построить графики изменения отношений МПЧ / ОРЧ и ОРЧ / НПЧ при возрастании интенсивности ММН ЭК (р = 10-3 ^10-2) ионосферы (рис. 3).

Анализ рис. 3 показывает, что по мере увеличения уровня диффузности (интенсивности ММН ЭК) ионосферы от в = 10-3 до 10-2 величина ОРЧ в односкачковой ДКМ радиолинии снижается по отношению к МПЧ с традиционных значений           до            и повышается орч , м         орч , м по отношению к НПЧ с обычных значений fорч - fн/0,2 до fорч - fн/0,4.

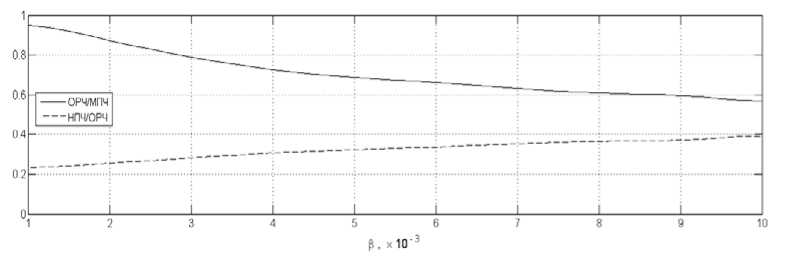
Рис. 3. Изменение соотношений между оптимальной рабочей и максимально применимой частотой, а также оптимальной рабочей и наименьшей применимой частотой в ДКМ радиолинии при возрастании интенсивности неоднородностей ионосферы

Выводы:                                 2.

• 1.    Разработана 6-этапная методика определения оптимальной рабочей частоты ( f =   ) од-

• 0 орч             з.

• 2.    В результате анализа влияния роста диф-фузности ионосферы было установлено, что по мере увеличения интенсивности мелкомасштабных неоднородностей ионосферы на порядок (от ^6. 3 = 10 ^{- 3} до 10 -2 ) величина оптимальной рабочей частоты в односкачковой ДКМ радиолинии снижается по отношению к максимально применимой частоте почти в 2 раза и во столько же раз повышается по отношению к наименьшей при-  7.

носкачковой ДКМ радиолинии по критерию обеспечения максимального превышения отношения сигнал/помеха E 1 ( f 0 )/ E 1 (f 0 ) на входе .

приемника над техническим фактором T ( f , , Д') при заданном уровне диффузности ионосферы ( β ).                                                         ^5.

менимой частоте (рис. 3).