Влияние динамики процесса сверления на формирование погрешностей глубоких отверстий

Введение. Во многих областях машиностроения используются детали, имеющие глубокие отверстия [1]. Для получения глубоких отверстий, имеющих отношение глубины l к диаметру D равное или более 5, используются сверла, обладающие малой жесткостью в радиальном направлении особенно при обработке отверстий малого диаметра. Это зачастую приводит к появлению брака, связанного с геометрической неточностью отверстия, прежде всего с отклонением действительной оси отверстия от его идеальной оси и отклонениями диаметра отверстия в поперечных сечениях.

Постановка задачи. Изучение механизмов формирования погрешностей, возникающих при обработке отверстия из-за упругих деформационных смещений вершины инструмента, вызванных динамикой процесса сверления.

Построение модели. Рассматриваются составляющие силы, которые связаны с координатами упругих деформаций вершины инструмента, формирующими пространство состояния системы. В этом случае все внешние силы, не связанные с координатами пространства состояния, не принимаются во внимание.

При построении системы дифференциальных уравнений, описывающих динамику системы в радиальном направлении, ограничимся первой формой радиальных изгибных колебаний сверла. Тогда динамику системы необходимо рассматривать на основе анализа радиальных колебаний обобщенной массы, подвешенной к несущей системе станка на упруго-вязких подвесках (рис.1).

Рис.1. Эквивалентная схема механической системы

Необходимо проанализировать деформационные смещения вершины инструмента во вращающейся системе координат, для этого представим силы, действующие на сверло в координатах упругих деформаций инструмента, тогда в общем виде [2] уравнения динамики сверла в радиальных направлениях будет иметь вид:

M _; + H— + C Y = P y ( Y, S P , V P ) ,                        (1)

dt2       dt где M =

m ₁

m ₂

- матрица приведенных масс, Н - с 2 /мм; H =

h ₁ 0

h ₂

– матрица приведенных

коэффициентов диссипации, Н - с/мм; С =

c ₁

c ₂

– матрица приведенных коэффициентов

жесткости, Н/мм; Y = y ₁, y ₂ ^T – вектор отклонений сверла в радиальных направлениях, мм; P_Y ( Y , S _P , V _P ) = H P Yis ( Y , S _P , V _P ), P_Y2Y ( Y , S _P , V _P )| ^г - вектор-функций динамических характеристик (сил резания) по радиальным направлениям, H ; S _P – подача пиноли, мм/рад; V _P – скорость резания, мм/с. Отметим, что подача S _P и скорость V _P задают стационарную траекторию движения инструмента. Матрицы M , H и C определяют параметры подсистемы инструмента в ортогональных радиальных направлениях.

Следующие обстоятельства раскрывают связь деформационных смещений вершины инструмента с точностью отверстия.

– если координаты состояния смещаются от идеальной оси режущего инструмента за счет упругих деформаций и при этом отсутствует изгиб сверла, то в этом случае будет наблюдаться разбивка диаметра отверстия;

– если координаты состояния не только смещаются относительно оси вращения, но при этом наблюдается изгиб инструмента, то возможно формирование нового направления движения инструмента, что приведет к уводу оси отверстия.

Базовые уравнения динамики. Моделирование упругих радиальных деформаций режущего инструмента не представляет сложностей, если рассматриваются колебания в частотном диапазоне, ограниченном первой формой колебаний. Параметры уравнения (1) M , H и C могут быть идентифицированы на основе анализа колебательных реакций системы на импульсные 5 -образные воздействия и статических измерений жесткости сверла. Особое значение имеет представление радиальных составляющих сил P_Y1Y ( у 1 , у 2 ) и P _Y2Z ( у 1 , у 2 ) в координатах упругих деформаций, определяемых относительно стационарной траектории. Для раскрытия динамических характеристик примем базовую гипотезу образования сил, утверждающую, что силы на i -ом режущем лезвии сверла пропорциональны площади f_i срезаемого слоя материала заготовки соответствующим режущим лезвием сверла. Данная гипотеза не противоречит положениям теории резания металлов.

Рассмотрим схему деформирования сверла в радиальном направлении y ₁ и влияние упругих деформаций сверла на изменение площадей f_i срезаемых слоев каждым режущим лезвием, при этом будем исходить из того, что колебания имеют первую форму. Радиальное отклонение сверла в направлении y ₁ может быть представлено в виде поворота сверла относительно точки закрепления O₁ на угол α_O1 и одновременного поворота на угол α_O2 относительно точки O₂ (рис.2).

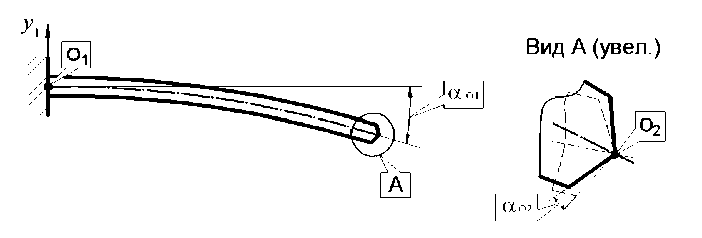
Рис.2. Схема деформирования сверла в радиальном направлении

Рассматриваемая схема деформирования сверла приводит к нелинейному изменению площадей f 1 ( y _J ) и f 2 ( y _J ) срезаемых слоев каждым режущим лезвием сверла (рис.3). В начале упругого деформирования сверла влияние угла α_O1 на смещение вершины инструмента будет больше (за счет вылета сверла), чем угла a_O2 , что приведет к уменьшению площади f 1 ( y _J ) и увеличению площади f 2 ( y _J ) , т.е. f _J ( y _J ) < f 2 ( y _J ) (рис.3, 6 ). По мере деформирования сверла, влияние угла α_O2 на смещение вершины инструмента будет увеличиваться, а угла α_O1 – уменьшаться, что приведет к увеличению площади f_j ( y _J ) и уменьшению площади f 2 ( y _J ) , в результате f , ( y _J ) = f 2 ( y _J ) (рис.3, в ). При дальнейшем деформировании в направлении y_J , площадь f _j ( y _J ) будет продолжать увеличиваться, а площадь f 2 ( y _J ) - уменьшаться, в результате f 1 ( У i ) > f 2 ( У i ) (рис.3, / ). Приведенная схема деформирования рассматривается для инструмента, обладающего симметричной геометрией режущей части, например, неравенство углов в плане ф ₁ и ф ₂ может привести к дополнительным изменениям площадей срезаемого слоя f _J ( У _J ) и f 2 ( y _J ) и соответственно к изменению сил резания.

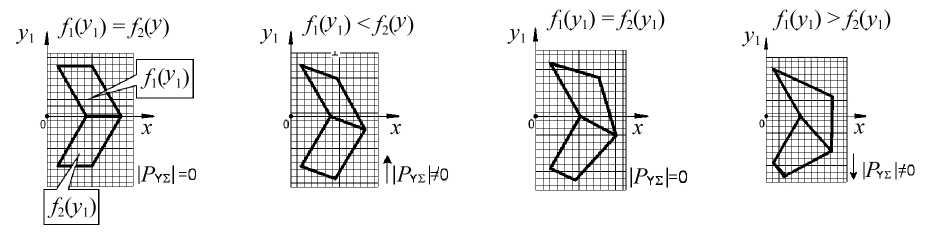
а )                                б )                               в )                             г )

Рис.3. Влияние отклонения сверла y1 на площади срезаемых слоев fj(У j)и f2(У j):

а –

^a OJ = ^a O2 = ⁰ ; ^{6 a} OJ >  ^a O2 ; в

^a OJ ^ 0, ^a O2 ^ ⁰ : ^f J = ^f 2 ; ^{r a} OJ <  ^a O2

Тогда динамическая характеристика P_YJY ( y _J ) , в силу базовой гипотезы, будет определяться значениями площадей f _j ( y _J ) и f 2 ( y _J ) :

P yj^ ( У j ) =РУЧ У j ) — P?( У j ) ,                                 (2)

p(4У J ) = P y f ( У J ) , i = J,2 ,                                  (3)

где рУ¹ ) ( y _J ) - радиальная составляющая силы резания на i -ом режущем лезвии в направлении y _J , Н; р _y - коэффициент резания (удельная сила резания) по радиальному направлению y _J , МПа; f i ( у _J ) - площадь срезаемого слоя на i -ом режущем лезвии, мм².

Одновременно изменение площадей срезаемых слоев f 1 ( у 1 ) и f 2 ( у 1 ) приводит к образованию составляющей силы резания, действующей в радиальном направлении y ₂ . Отметим, что возникновение деформации сверла в направлении y ₂ , вызывает одновременное увеличение переднего угла резания на одном лезвии сверла и уменьшение переднего угла на другом лезвии. Так как силы зависят от величины переднего угла режущего инструмента, то за счет увеличения упругих изгибных деформаций, будет возрастать значение радиальной составляющей силы резания, что приведет к еще большему увеличению деформации сверла в радиальном направлении. Таким образом, при смещении вершины сверла в радиальном направлении y ₁ , возникают как составляющая силы P_YXY ( у 1 , у ₂ ) , так и силы P _Y2Z ( у 1 , у ₂ ) , действие этих сил будет направлено по ортогональным направлениям y ₁ и y ₂ соответственно.

Для дальнейшего анализа важны следующие обстоятельства, которые приведены ниже: – упругие деформации сверла будем рассматривать как стержень круглого сечения, известно, что в этом случае, независимо от выбранной системы координат, матрицы M , H и C в системе (1) являются не только диагональными, но и имеют равные значения коэффициентов m_i , h_i и c_i , деформация же сверла осуществляется по направлению действия силы. В этом случае можно выбрать произвольную систему координат, при этом матрицы M , H и C являются независимыми от выбранной системы координат;

– примем допущение о том, что ориентации сил резания в зависимости от деформации сверла являются постоянными.

Эти обстоятельства позволяют при оценке деформации сверла выбрать новую систему координат у 0 - у 0 , повернутую относительно системы координат у 1 - у ₂ на угол у , который определяется ориентацией силы в системе координат у 1 - у ₂ , тогда деформационные смещения в направлении y ₁ ⁰ будут вызывать изменение силы, действующей в этом же направлении (рис.4).

Рис.4. Преобразование исходной системы координат у ! — у 2 к новой системе координат у 0 — у 0

Можно проанализировать движение системы в направлении у 0 ( у ) :

^т<Мг+^ ^+с у=P^. ⁽ у )

dt ²      dt

Уравнение (4) на фазовой плоскости запишем относительно фазовых координат:

dy =	z
ddt”
dz =	1
. dt	m

⁽ P YX. ⁽ У ) - hz - cy )•

Анализ динамики системы. Вопрос смещения положения вершины сверла относительно его идеального осевого положения за счет упругих деформаций, а также исследование точки равновесия и области ее притяжения можно решить через фазовые портреты системы для случая идентичности геометрических параметров режущей части сверла.

На рис.5, а показаны нелинейные зависимости изменения площадей f 1 ( у ) и f 2 ( у ) , а на рис.5, б соответствующая им нелинейная зависимость динамической характеристики резания Р ух ( У ) в радиальном направлении, которая вычислена по выражениям (2) и (3) при у 1 = у , данные для расчета имели следующие значения: диаметр сверла D = 12 мм, вылет сверла L = 150 мм, углы в плане ф ₁ = ф ₂ = 60 ° .

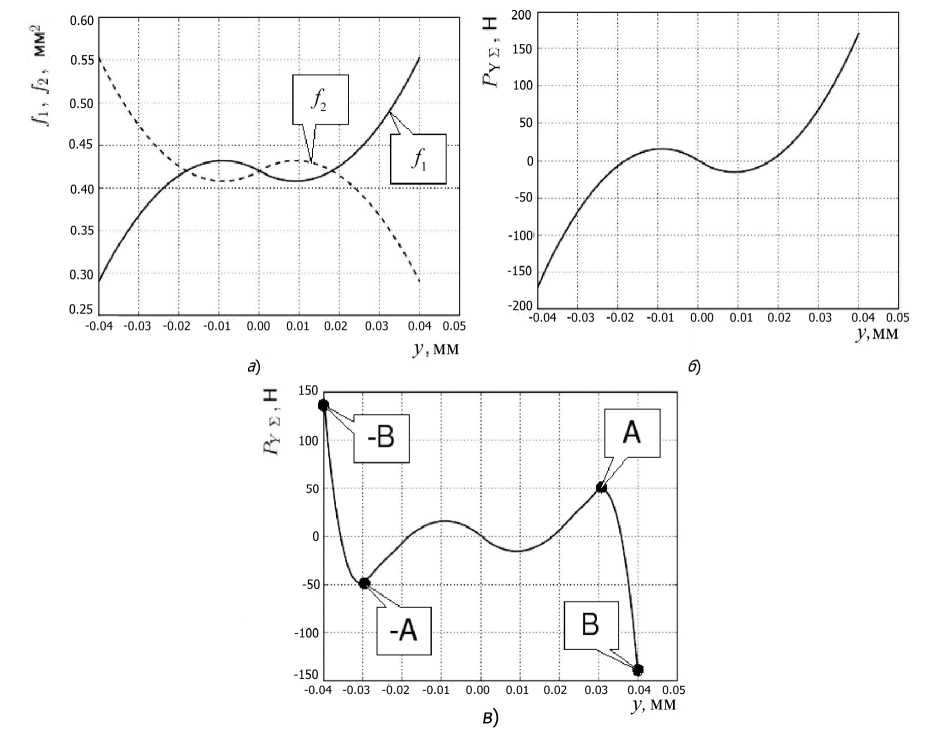
Рис. 5. Нелинейные зависимости: а - площадей f 1 ( у ) и f 2 ( у ) ; б - динамической характеристики Р у^ ( у ) без учета функции сближения F s ; в ) - динамической характеристики Р у^ ( у ) с учетом функции сближения F s

В процессе сверления по мере заглубления сверло соприкасается своей боковой поверхностью (ленточками) с цилиндрической поверхностью образуемого отверстия. В результате формируется нормальная сила контактного взаимодействия, которая направлена противоположно радиальному перемещению сверла. Нормальную силу контактного взаимодействия поверхностей сверла и отверстия можно описать функцией сближения FS [3], которая зависит от величины сближения поверхностей сверла и отверстия в радиальном направлении, глубины засверливания и площади контакта поверхностей:

F S = g ( 5 ( У ) ,l засв ^, ^ S ) ,                                         ⁽⁶⁾

F S ^ F S max : ^{8 (} y ) ^ ⁸ min , l засв > l засв max ,                              (7)

где 8(у) - расстояние между поверхностями сверла и отверстия в радиальном направлении, мм; lзасв – глубина засверливания, мм; wS – ширина ленточки сверла, мм, wS = const .

Влияние функции сближения F S на динамическую характеристику P Y^ ( у ) проявляются в образовании участков { - B ; - A } и { A;B } (рис.5, в ).

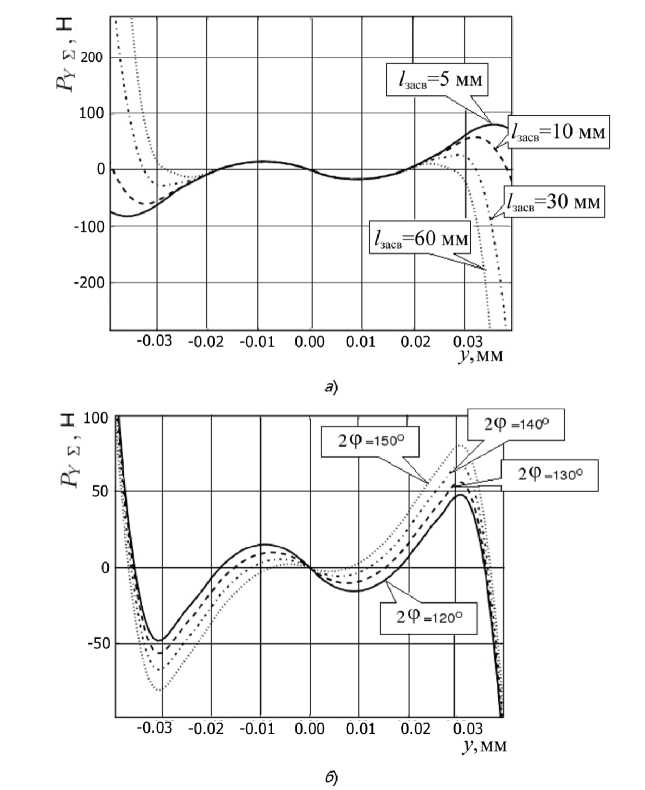
Рис.6. Влияние на динамическую характеристику

PYY (y ) :

а - глубины засверливания l _засв ; б - двойного угла в плане 2 ф

На рис.6 показано изменение динамической характеристики P Y^ ( у ) в зависимости от глубины засверливания l засв (рис.6, а ) и двойного угла в плане 2 ф сверла (рис.6, 6 ).

При увеличении глубины засверливания l _засв точки - A и A (рис.5, в ) приближаются к значению P Y^ ( у ) = 0 , что является непосредственным проявлением влияния функции сближения F_S , значение которой увеличивается с увеличением глубины засверливания l _засв . Приведены фазовые портреты численного решения системы (5) для значений динамической характеристики P Y^ ( у ) (рис.6, а ). Как можно наблюдать при малых значениях глубины засверливания (рис.7, а ), при незначительном влиянии функции сближения F_S на сверло, на фазовой плоскости образуются три точки равновесия Q ₁ , Q ₂ и Q ₃ со своими областями притяжения. Эти области разделены седлообразными сепаратрисами.

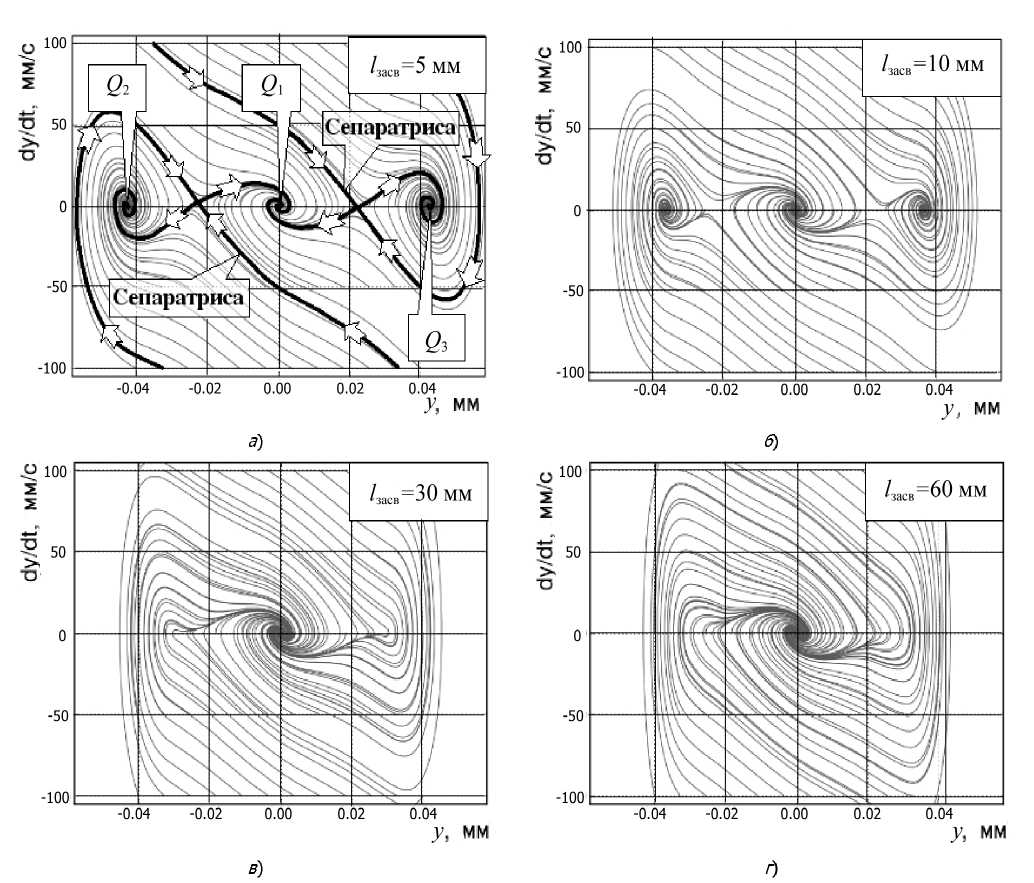
Рис. 7. Фазовые портреты решений системы (5) для динамической характеристики PY^ (у), соответствующей различным глубинам засверливания l засв : а - l засв = 5 мм; б - PY^ (у) мм; в - l засв = 30 мм; г - l засв = 60 мм

Подчеркнем, что точка равновесия Q1 находится на идеальной оси вращения сверла, совпадающей с осью вращения шпинделя. Точкам равновесия Q2 и Q3 соответствуют упругие стационарные деформации инструмента относительно оси его вращения. Поэтому, если система находится в точках равновесия Q2 и Q3 , то, во-первых, изменяется диаметр обрабатываемого отверстия, во-вторых, резко возрастает вероятность увода сверла. Поэтому принципиальное значение имеет область притяжения точки равновесия Q1 . По мере увеличения глубины за- сверливания lзасв , точки равновесия Q2 и Q3 вырождаются, а область притяжения точки Q1

занимает всю фазовую плоскость.

Проанализируем преобразование фазовых портретов в зависимости от величины двойного угла в плане 2 ф сверла (рис.8).

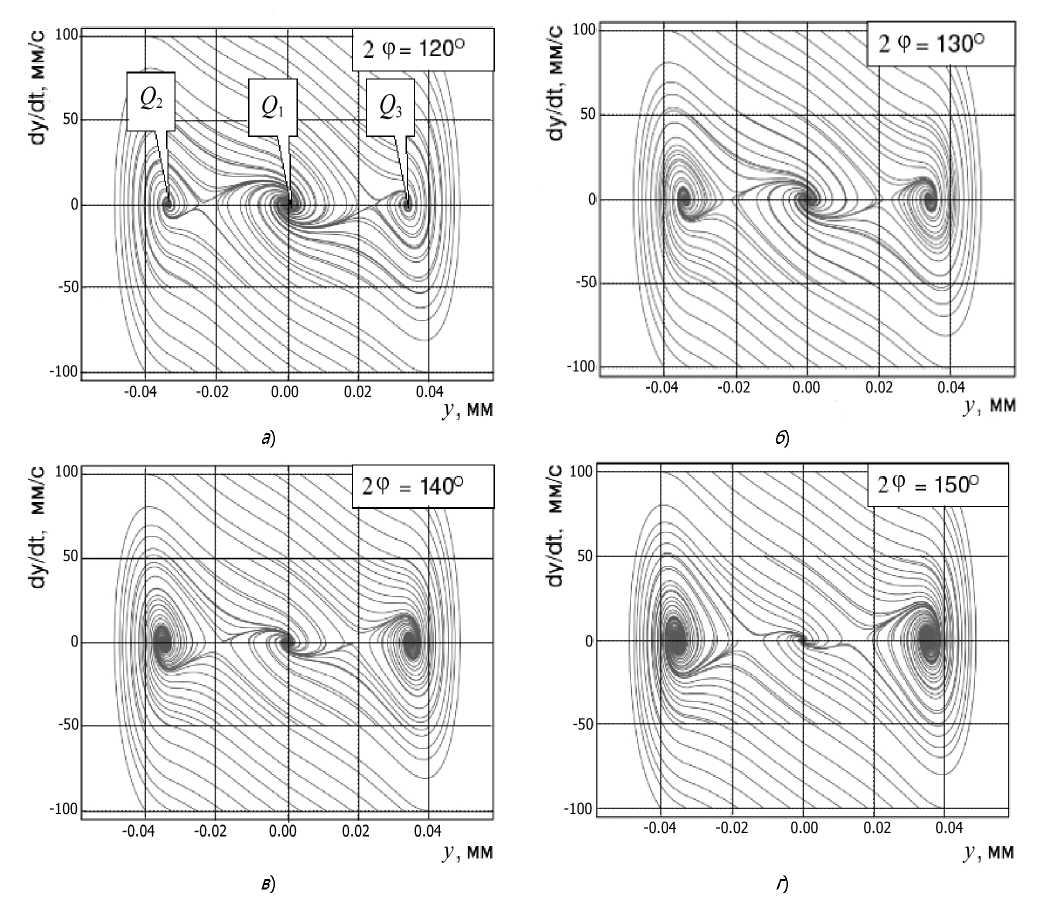
Рис. 8. Фазовые портреты решений системы (5) для динамической характеристики

PYS (y), соответствующей различным значениям двойного угла в плане 2ф сверла:

а - 2 ф = 120 O ; б - 2 ф = 130 O ; в - 2 ф = 140 O ; г - 2 ф = 150 O

На фазовых портретах (рис.8) также отчетливо проявляются три стационарные точки Q1 , Q2 и Q3 с областями притяжения соответственно. Но в отличие от ранее рассмотренного случая увеличение угла 2ф способствует расширению областей притяжения точек равновесия Q2 , Q3 и сужению области притяжения стационарной точки Q1 , таким образом, вероятность стабилизации системы в начале координат фазовой плоскости снижается. С технологической точки зрения увеличение двойного угла в плане 2ф сверла увеличивает вероятность увода оси отверстия. Таким образом, можно сделать вывод, что уменьшение двойного угла в плане позволяет снизить вероятность отклонения вершины сверла, однако необходимо помнить, что уменьшение угла 2ф может отрицательно сказаться на других показателях процесса обработки, например, с уменьшением угла 2ф затрудняется отвод стружки из зоны резания вследствие ее пакетирования. Таким образом, фазовые портреты показывают, что на величину области притяжения точки равновесия Q1 принципиальное влияние оказывает величина двойного угла в плане 2ф (рис.8).

Все рассмотренные выше случаи относились к режущему инструменту, обладающему идеальными и симметричными режущими свойствами. Однако если режущие свойства лезвий сверла отличаются друг от друга, то имеет место смещение точки равновесия Q ₁ .

Изменение режущих свойств лезвий сверла может быть вызвано следующими факторами:

• –    погрешность заточки лезвий сверла, проявляющаяся в наличие эксцентриситета вершины сверла относительно его идеальной оси;

• –    неравномерность развития износа;

• –    анизотропия физических свойств обрабатываемого материала;

• –    неравномерность поступления СОЖ в зону резания и прочими факторами.

Влияние на смещение точки равновесия Q ₁ и изменение фазового портрета системы асимметрии геометрии режущей части сверла проявляется в наличии эксцентриситета вершины сверла относительно его идеальной оси.

На рис.9, б показано изменение динамической характеристики P Y^ ( у ) в результате эксцентриситета вершины сверла ( e * 0 ) (рис.9, а ).

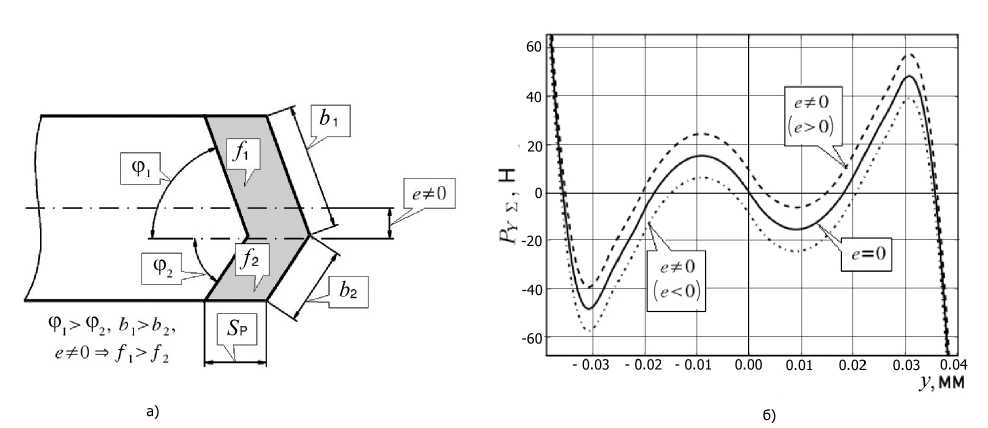
Рис. 9. Влияние неравенства углов в плане Ф 1 и Ф 2 :

а – на образование эксцентриситета, e ; б – динамическую характеристику,

P ys ⁽ y )

Эксцентриситет e вызывает не только изменение областей притяжения точек равновесия (область притяжения точки Q ₃ больше, чем точки Q ₂ ), но и смещение точки равновесия Q ₁ относительно начала координат фазового портрета, т.е. относительно идеальной оси вращения сверла, что приводит к возникновению геометрических погрешностей отверстия (рис.10).

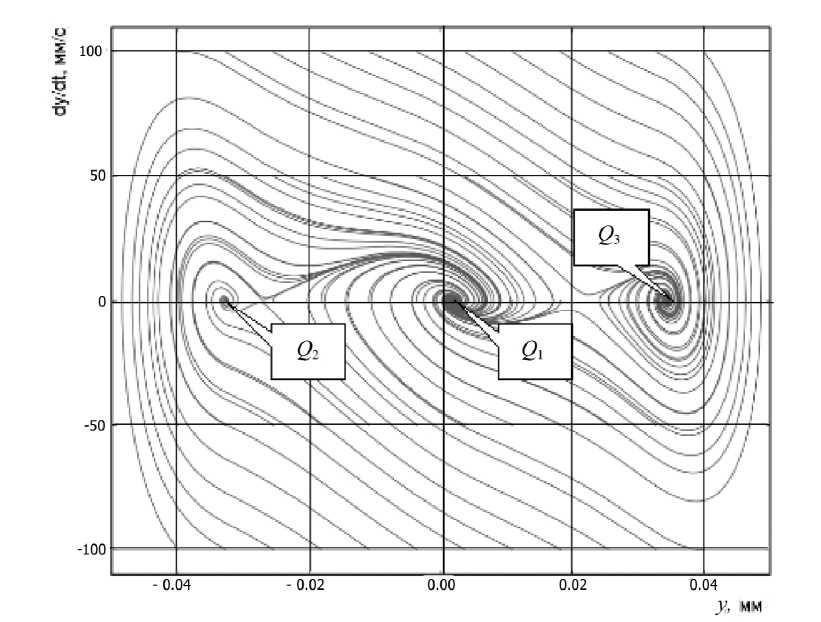
Рис.10. Фазовый портрет решений системы (5) для динамической характеристики при наличии эксцентриситета

( e >  0 ) вершины сверла