Влияние фактора сезонности на инвестиционную активность малого бизнеса в регионе

Потребность малого бизнеса в инвестициях в сложившейся экономической ситуации сегодня ни у кого не вызывает сомнений, так же, как и сложность привлечения этих самых инвестиций. Поэтому инвестиционная активность субъектов малого бизнеса является крайне важной составляющей предпринимательской деятельности. Вне всякого сомнения, малый бизнес особенно чувствителен к различным колебаниям и рискам, исходящим из внешней среды [1]. Одним из таких системообразующих факторов является сезонность. При этом адекватной информации об инвестиционной составляющей деятельности малого, а особенно, микробизнеса, крайне мало [2]. В связи с этим предлагается для оценки влияния фактора сезонности использовать косвенные данные, которые, по мнению автора, достаточно полно характеризуют исследуемый процесс инвестиционной активности.

В качестве релевантной по отношению к инвестиционной активности малого бизнеса информации были использованы данные о выдаче микрозаймов малому бизнесу Архангельским региональным фондом микрофинансирования в рамках государственной программы развития предпринимательства. Сегодня на региональном уровне Фонд как микрофинансовая организация является одним из основных институтов, входящих в инфраструктуру поддержки предпринимательства. За время своей работы с декабря 2010 года по сегодняшний день им было выдано более 900 займов на общую сумму свыше 500 млн. руб., поэтому данные о динамике портфеля Фонда можно считать достаточно репрезентативными для описания инвестиционных потребностей малого бизнеса в регионе [3].

Первичный анализ имеющейся информационной базы, представленной Фондом, позволяет сделать вывод о том, что исследуемый показатель – выданные микрозаймы, обладает рядом особенностей, таких как:

• -    короткий динамический ряд (длина ряда не превышает 3 – 5 лет, то есть 36 – 60 точек);

  - ярко выраженная сезонность показателя;

  - отсутствие ряда данного показателя в ежедневной динамике.

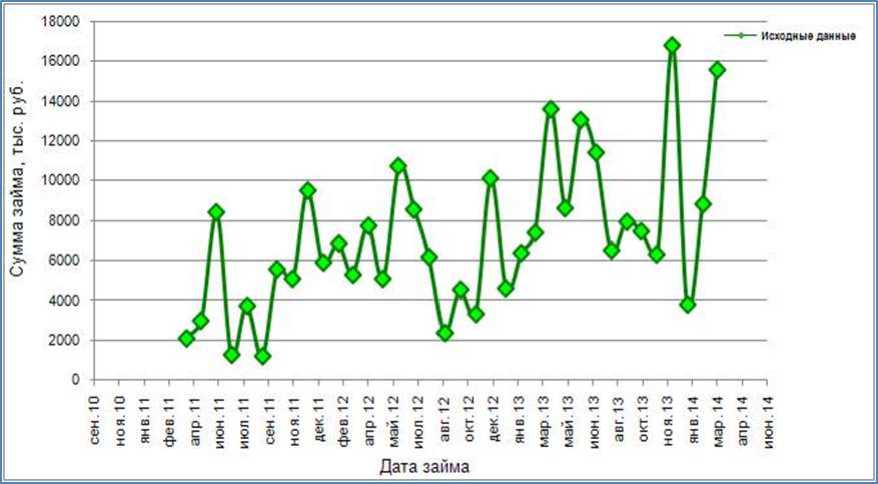
Рисунок 1 – Динамика объёмов выданных микрозаймов за период с апреля 2011 г. по март 2014 г.

Приведенные выше факторы обуславливают применение эконометрических методов [4] для дальнейшего анализа динамики временного ряда, визуализированного на рисунке 1.

Исходные данные, подвергаемые математико-статистической обработке, должны удовлетворять следующим требованиям: уровни исследуемого показателя обязательно должны быть сопоставимы, однородны и устойчивы, а их число должно быть достаточно велико. Только если все указанные предпосылки выполняются, то временной ряд считается пригодным для моделирования.

Исследуемый в статье временной ряд с помесячной динамикой был сформирован на основе 36 точек (объёмы выданных микрозаймов, тыс. руб.). Было проверено, что требования сопоставимости и полноты исходных данных для него выполняются. По графику на рисунке 1, видно, что изменения последовательных уровней ряда не являются хаотичными, и визуально можно проследить наличие устойчивой закономерности в изменении уровней ряда, что свидетельствует об устойчивости исходных данных.

При проведении качественного анализа аномальных уровней ряда с использованием критерия Ирвина было выявлено, что причинами аномалий являются ошибки II рода, которые возникли из-за воздействия факторов, имеющих объективный характер. Согласно экспертному мнению опрошенных специалистов выявленные аномальные уровни ряда несут в себе значительную смысловую нагрузку, а именно:

• -    октябрь 2011 г., декабрь 2011, 2012 и 2013 гг. - данным уровням ряда соответствуют наибольшие значения объёмов выданных займов, что объяснимо периодом подведения итогов финансово-хозяйственной деятельности предприятий, когда возрастает необходимость в привлечении дополнительного финансирования;

• -    январь 2013 и 2014 гг. - первая декада января является нерабочей, чем и вызвано традиционное падение деловой (и в первую очередь инвестиционной) активности;

• -    апрель 2013 г., февраль и март 2014 г. - происходит скачок объёмов выданных займов в силу того, что рассматриваемый весенний период совпал с открытием торгов на подряды и активным объявлением тендеров, для участия в которых бизнесу необходимы дополнительные инвестиции;

• -    июнь и июль 2011 г., июнь 2012 и 2013 гг., август 2013 г. – этот временной период характеризуется повышением объёмов выданных займов, что в свою очередь явилось следствием массовой активности региональных и федеральных СМИ по вопросам предпринимательства. Таким образом, в данный период сработал эффект «навязчивой рекламы».

В силу того, что выявленные аномалии вызваны причинами второго рода, то они устранению не подлежат, а значит требование однородности исходных данных также выполнимо. Таким образом, все предпосылки к моделированию выполняются.

Предварительный анализ динамики исследуемого показателя, позволяет выдвинуть гипотезу о составных компонентах модели, включая фактор сезонности. Стоит заметить, что выдвинутая гипотеза на данном этапе имеет эмпирическое происхождение, хотя бы по причинам, отмеченным в начале статьи.

Автокорреляционная функция (АКФ) исследуемого временного ряда (ВР) представлена в таблице 1, ее визуализация приведена на рисунке 2.

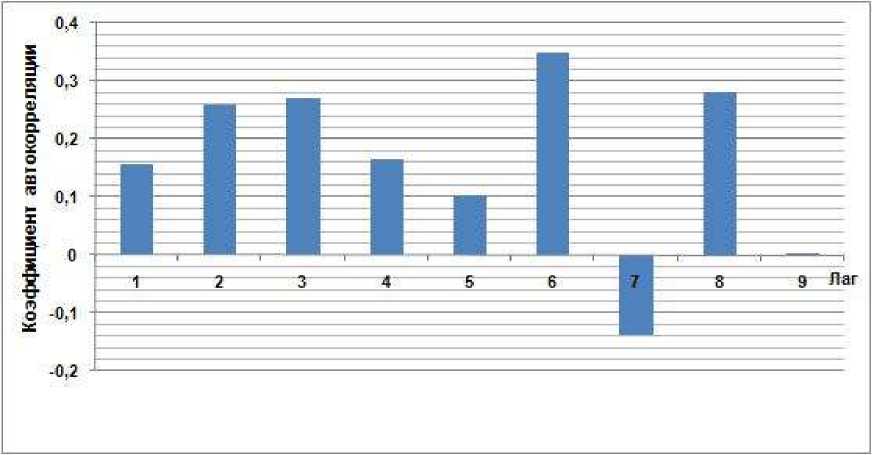
Рисунок 2 – Коррелограмма АКФ объёмов выданных микрозаймов

Коррелограмма позволяет выдвинуть гипотезы: о наличии в ВР линейной тенденции, о которой также свидетельствует убывание коэффициентов автокорреляции с лагами 3 – 5; а также о периодической компоненте, включающей в себя несколько гармонических колебаний с различными циклическими частотами.

Таким образом, исследуемый ВР может предположительно быть аппроксимирован тренд-сезонной моделью следующего вида :

Y(t ) = f ( t ) + s ( t ) + z (t ),               (1)

где f(t) - тренд, S(t) - сезонная компонента, s(t) - случайная (остаточная) компонента. В качестве модели-кандидата тренда используем линейную функцию, параметры которой оценим с помощью метода наименьших квадратов (МНК).

Таблица 2 – МНК-оценка параметров линейного тренда в MS Excel

Таблица 1 – АКФ объёмов выданных займов

Лаг	1	2	3	4	5	6	7	8	9
Коэффициент автокорреляции	0,15 5	0,26 1	0,27 1	0,16 6	0,10 3	0,35 0	0,138	0,28 0	0,00 3

Регрессионная статистика
Множественный R	0,5532
R-квадрат	0,306
Нормированный R-квадрат	0,2856

Стандартная ошибка	3191,9603
Наблюдения	36

		df	SS		MS		F
Регрессия		1	152735222,8		15273522 3		14,9907 8
Остаток		34	346412762,5		10188611
Итого		35	499147985,3
Коэффициенты уравнения регрессии			Стандартна я ошибка определения коэффициент ов	t -статистик а, расчётное		Вероятность ошибки		Нижние 95% -пределы		Верхние 95% - пределы
Свободны й член	3613		1042,1963	3,4667		0,0014		1495,004 6		5731,0002
Переменн ая t	198,27 8		51,2108	3,8718		0,0005		94,2048		302,3508

Таким образом, получаем следующее уравнение тренда: f ( t ) = 198,28 - 1 + 3613,002.

Результаты таблицы 2 показывают, что тренд статистически значим на 5%-м уровне (расчетное значение критерия Фишера Fфакт. = 14,99 при Fкр. = 4,13); но при этом он объясняет только 30,6% изменений объёмов выданных микрозаймов.

Как было отмечено выше, для моделируемого процесса характерна сезонность. Моделирование сезонных колебаний «очищенного» от тренда ряда проведено с использованием гармонического анализа, основанного на использовании рядов Фурье (3). Соответствующие расчеты параметров приведены в таблицах 3 и 4.

V   V Г        (  2 П 1 • У , •   • „ (  2 1 1 ^ I           • •  1                       (3) Y, =/ a^ - cos-- kt + b, - sin-- kt , k = 0,..., N - 1. k  ^ L k    I   N   J   k   I   N  J_ Таблица 3 – Параметры при cos тригонометрического ряда Фурье
k	ak		k	ak
0	0,000		10	-320,225
1	108,508		11	-365,730
2	-1004,811		12	-501,253
3	1459,337		13	-1411,662
4	201,388		14	-1202,213
5	375,249		15	-335,559
6	-494,969		16	56,930
7	421,468		17	-127,333
8	-60,567		18	2486,439
9	445,222

Таблица 4 – Параметры при sin тригонометрического ряда Фурье

k	bk		k	bk
0	0,000		10	644,868
1	-286,298		11	504,963
2	6,484		12	1731,751
3	-244,823		13	482,154
4	815,947		14	-34,662
5	-220,724		15	-508,672
6	-1387,801		16	177,308
7	331,713		17	73,878
8	-182,471		18	0,000
9	1007,172

Для определения качества параметров модели сезонной компоненты тестировались информационные критерии: байесовский, Акаике и Ханнана-Куинна. Необходимые для расчета критериев амплитуды (4) приведены в таблице 5.

A = ^b' .              (4)

Таблица 5 – Значения амплитуды k -го гармонического колебания

k	Ak		k	Ak
1	306,171		10	719,999
2	1004,832		11	623,496
3	1479,730		12	1802,835
4	840,432		13	1491,731
5	435,352		14	1202,713
6	1473,427		15	609,382
7	536,348		16	186,223
8	192,260		17	147,213
9	1101,190		18	2486,439

Визуализация результатов таблицы 5 представлена на рисунке 3.

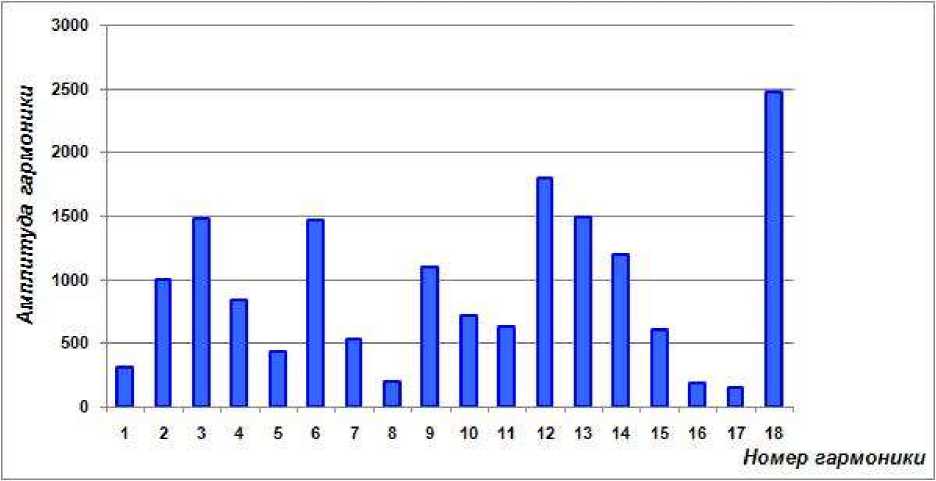
Рисунок 3 – Амплитуды гармонических колебаний

Отметим, что в данном случае байесовский критерий по определенному ряду причин оказался неприемлемым.

Расчет значений критерия Акаике ( AIC ) по формуле (5) показал, что в сезонную компоненту моделируемой динамики выданных микрозаймов войдут гармоники с номерами 18, 12, 13, 3, 6, 14, 9, 2, 4.

AIC = 2 m + n

К

( n-1   A ln E £t

V t = 0     J

аналогичному результату приводят расчеты по критерию Ханнана-

Куинна (HQ) по формуле 6 – для включения в сезонную компоненту попали гармоники с номерами 18, 12, 13, 3, 6, 14, 9, 2.

Г N n -1 \

Так как для аддитивныXn (1моД+пейп E ^евонными компонентами, параметры которых определены с помоЩью 0информационных критериев Акаике и Ханнана-Куинна, R2 = 0,82 и R2 = 0,8, соответственно, то выбор остановим на первой из них. Таким образом, с учетом сезонности уже 82% изменения объёмов выданных микрозаймов объясняется временным диапазоном. Аналитическое представление построенной аддитивной модели будет задано следующим тригонометрическим рядом Фурье (7):

Yt = 3613,002 + 198,28 t + 2486,439cos		j ( -n t ) - 501,253cos |	'  2 n ^    3	t | + 1731,751sin | - — t |- )        ’         I    3   )
- 1411,662cos |	t )^154^	- — t | + 1459,337cos |-v 18   )                 I		П t I- 244,823sin I - n t I- 6 )              I 6 )
- 494,969cos |	- - 1 |- 1387,801sin f - 3 )         ’         I	П t I- 1202,213cos I 3   )         ’          I	7 n - t 9	I- 34,662sin I - — t | + )      ’         I    9   )
+ 445,222cos f	- П t V 1007,172sin f - 2 )         ,         I	П t V 1004,811cos f 2 )         ’         I	n — t 9 ))	+ 6,484sin f- П t V I 9 )
+ 201,388cos | ■	- — t | + 815,947sin | - 9   )                I	2 n I t . 9   )		(7)

Фактическая и модельная динамики объёмов выданных микрозаймов за период апрель 2011 г. – март 2014 г. представлены на рисунке 4.

После выделения тренда и сезонной составляющей результаты проверки остаточной компоненты показали следующее.

Случайных характер остатков обусловлен количеством поворотных точек p = 30 (при n=36 на 5%-м уровне значимости критерий «пиков» дает pрасч.=17).    Соответствие нормальному закону распределения подтверждается значением R/S-критерия, равным 4,11 и попадающим в табличный интервал от 3,67 до 5,16. Равенство нулю математического ожидания уровней ряда остатков проверено по t-критерию Стьюдента: t   =-0,11 < 2,03 = t расч              табл . При этом следует отметить наличие автокорреляции в остатках – критерий Дарбина-Уотсона дает значение DW=3,09. Обнаружение автокорреляции в ряду остатков является естественным результатом, объясняемым наличием в исследуемой динамике нескольких наложенных друг на друга гармонических колебаний.

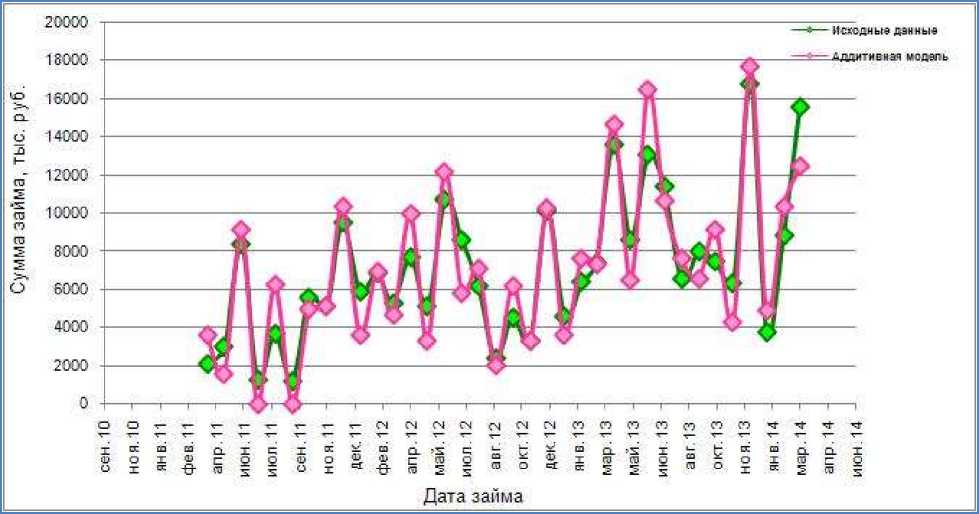
Рисунок 4 – Динамика объёмов выданных займов с апреля 2011 г. по март 2014 г.

Таким образом, аддитивная модель (7), аппроксимирующая процесс выдачи микрозаймов за период апрель 2011 г. – март 2014 г., является достаточно адекватной и обладает хорошим уровнем точности. Как уже отмечалось выше, полученная динамика, по мнению ряда опрошенных региональных экспертов, достаточно хорошо отражает системообразующую тенденцию инвестиционной активности субъектов малого бизнеса, по крайней мере тех, которые представлены в легальном секторе экономики.

Проведённые по модели прогнозные расчеты на март 2015 г. - апрель 2016 г. подтверждаются фактическими данными Фонда за этот период. Таким образом, верификация модели свидетельствует о её приемлемом качестве.

Как показал приведенный выше модельный пример, сезонность является крайне существенным фактором, влияющим на малый бизнес. Предложенную модель можно использовать, по крайней мере, в качестве некоего «зеркала», отражающего инвестиционные потребности малого бизнеса, а также основы для расчета индикативных показателей его инвестиционной активности на региональном уровне.