Влияние фазовых диаграмм направленности щелевых излучателей на диаграмму направленности турникетной щелевой антенны

Турникетные антенны широко используются в качестве передающих антенн для излучения электромагнитных волн горизонтальной поляризации. Первые антенны, созданные в нашей стране и за рубежом для передачи телевизионных сигналов, представляли собой турникетные антенны, в которых в качестве излучающих элементов использованы, по существу, щелевые излучатели. В оригинальных работах щелевые излучатели назывались плоскостными вибраторами [1, 2]. В настоящее время турникетные антенны со щелевыми излучателями широко применяются для излучения телевизионных сигналов в метровом диапазоне волн. С переходом в дециметровый диапазон ранее предложенные конструкции антенн оказались не реализуемыми [3]. Задача создания новых, оригинальных, конструкций антенн обусловила интерес к теории щелевых антенн, в частности, к их фазовым диаграммам направленности.

Рассмотрим модель турникетной антенны, состоящую из двух взаимно перпендикулярных элементарных щелевых излучателей, выполненных на идеально проводящих лентах. Ленты имеют бесконечную протяжённость в направлении, параллельном оси щели (в направлении, параллельном оси Oz на рис. 1), и конечную ширину в ортогональном направлении. Щели на рис. 1 представлены имеющими конечную ширину. Предполагается, что при размещении антенны на местности ось Oz будет направлена вертикально. На рис. 1, б показано сечение турникетной антенны плоскостью, перпендикулярной к вертикальной оси антенны. Периметр каждой ленты в сечении равен L. Ширина каждой ленты соответственно равна L/2 .

Рассмотрим амплитудную и фазовую ДН одного щелевого излучателя при различных значениях отношения периметра ленты L к длине волны А: ЦХ. Предположим, что щели расположены в цен-

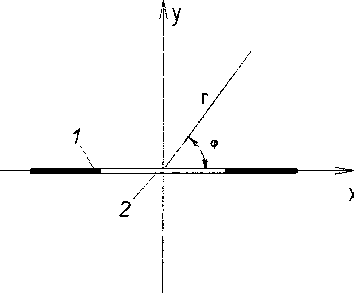
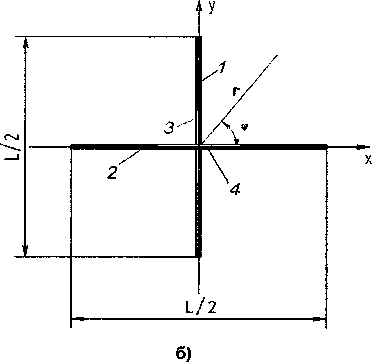
Рис. 1. Система координат (а): 1 - лента; 2 - щель на ленте; вид турникетной антенны в сечении ортогональном к вертикальной оси антенны (б): 1,2- ленты; 3 - щель на ленте 1; 4 - щель на ленте 2

тре ленты. Тогда для вычисления комплексной ДН щелевого излучателя воспользуемся следующей формулой [4]:

Н = i-HL rXZB

1-2 £ /^+1 .     р=0

Я^рС^О)

^ы (рСо,О)^+1[рсЦ U„+1 (рС0,Ф) , (1)

где Н - напряжённость магнитного поля в дальней зоне излучателя; U - напряжение; I - длина щелевого вибратора; (г,ф)- полярные координа

ты; Z^ - волновое сопротивление свободного пространства; Я_2/?+1(рС_о,О) - производная радиальной нечетной функции Матье-Бесселя 2р+1 порядка Js_2p+\ (РС₀,Рг) от аргумента рг попеременной г при г = г₀ = 0 ; Я5^₊₁ (рС_о,О) - производная радиальной нечетной функции Матье-Хан-келя второго рода 2р+1 порядка Я^²-^ (рС₀,Рг) от аргумента рг по переменной г при г = г₀ = 0 ; se₂p+i (Р^щф) ^- угловая нечетная функция Матье 2р+1 порядка для параметра рС₀ от аргумента ф [5, 6]. При выполнении данной работы для функции se_2/?+i (РС₀,ф) использована нормировка, приведенная в [7]. 2С₀- расстояние между фокусами,

Со =

А

; р - постоянная распространения, р =

2л

Т

Поясним величину параметра Со . Формула (1) получена как частный случай решения задачи дифракции плоской волны на эллиптическом цилиндре путем перехода от эллипса к ленте. При переходе от эллипса к ленте малая полуось эллипса принимается равной нулю. При этом большая по

луось эллипса равна расстоянию от начала координат до края ленты. Таким образом, постоянная Со при переходе к ленте оказывается равной половине ширины ленты.

При вычислении комплексных ДН множитель

—-— перед скобками в формуле (1) приравняем к XrZB единице. Обозначим комплексную амплитуду источника первого щелевого излучателя йтХ, комплексную амплитуду источника второго щелевого излучателя йт2 • Тогда комплексная диаграмма направленности первого щелевого излучателя Fx (ф) пропорциональна Uml и функции Н^), вычисляемой по (1). Комплексная диаграмма направленности второго щелевого излучателя F2 (ф)

пропорциональна U_mX и функции Я1 ф + —

При вычислениях по формуле (1) применялась нормировка эллиптических функций, предложенная в работе [7]. Основным достоинством применяемой нормировки и предложенной в [7] системы координат является то, что формулы для расчёта составляющих напряжённости поля не 2С0 содержат нормирующих множителей, вычисление которых сопряжено с громоздкими расчётами.

Фазовую ДН щелевого излучателя вычислим по формуле

6(ф) = arctg ----:---- .                     (2)

V 7 (КеЯ(ф))

Здесь 9(ф) - функция зависимости фазы напряжённости поля от полярного углаф; 1т(Я)-мнимая часть комплексной ДН щелевого излучателя; Ке(Я)- реальная часть комплексной ДН щелевого излучателя.

Для вычисления комплексной ДН по формуле

(1) и фазовой ДН по формуле (2) была написана программа в среде MATLAB. На рис. 2, 4 и 6 приведены амплитудные ДН, на рис. 3, 5 и 7 - фазовые ДН, полученные в результате расчётов по формулам (1) и (2) при различных значениях L / X

Представленные на рис. 4 и 6 амплитудные ДН с графической точностью совпадают с диаграммами направленности в работе [4, с. 226].

Перейдём теперь к рассмотрению ДН турникетной антенны.

Для формирования круговой диаграммы направленности расположим ленты взаимно перпендикулярно, как указано на рис. 1. Пусть амплитуда напряжения |<7mi| источника, возбуждающего щель 2 на ленте 1, равна амплитуде напряжения |(/т21 источника, возбуждающего щель 4 на ленте 3, фазы напряжений UmX и йтг отличаются друг от друга на 90°: йтг = йтХе 2 .

Тогда комплексная ДН первого щелевого излучателя F_x (<р) пропорциональна й_тХ и напряжённости магнитного поляН(ф)> найденной по (1) в предположении, что множитель U= 1. Комплексная ДН второго щелевого излучателя /₂ (ср)

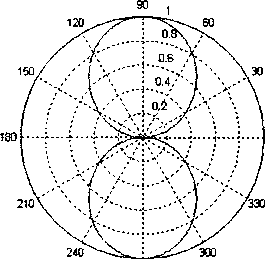
Рис. 2. Амплитудная ДН щелевого излучателя, L/X = 1

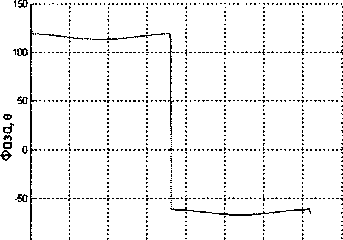
.1(Ю1--------------I--------------i--------------i---------------1---------------i---------------i---------------1---------------1

0     50     100    150    200    233    303    350    403

Угол, Ф

Рис. 3. Фазовая ДН щелевого излучателя, LjX = 1

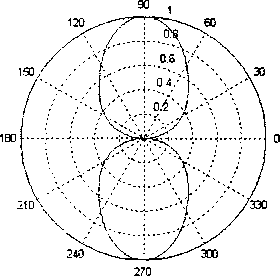
Рис. 4. Амплитудная ДН щелевого излучателя, L/X = 2

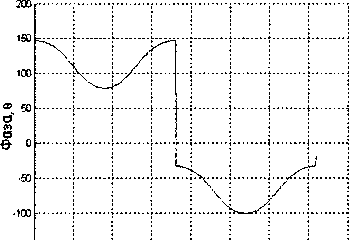
.1501--------------1---------------1---------------1---------------1---------------1--------------1---------------!---------------i

0      50     100    150    200    250    300    350    400

Угол, v

Рис. 5. Фазовая ДН щелевого излучателя, L/X = 2

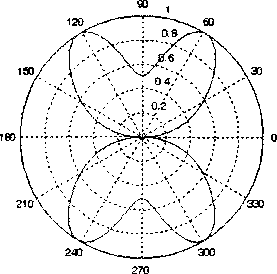
Рис. 6. Амплитудная ДН щелевого излучателя, L]X = 4

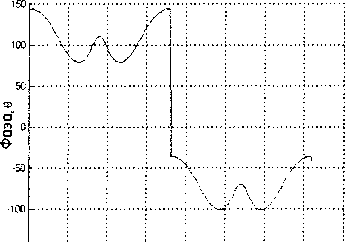
.,5П___I_______________I_______________I_______________i_______________I_______________I_______________I---------------1

0      50     100    150    3X1    250    300    350    400

Угол, Ф

Рис. 7. Фазовая ДН щелевого излучателя, LjX = 4

пропорциональна U_m2 и напряжённости магнитного поля Н(ц>+— ), найденной по (1) в предположении, что множитель (7=1.

Сравним диаграммы направленности турникетной антенны, вычисленные без учёта фазовых ДН щелевых излучателей (что заведомо неверно), с диаграммами направленности, вычисленными с учётом фазовых ДН излучателей. Без учёта фазовых ДН излучателей иногда делают оценку амплитудной ДН турникетной антенны, когда в распоряжении имеются только экспериментально измеренные амплитудные ДН излучателей.

В первом случае (без учёта фазовых ДН излучателей) амплитудную ДН турникетной антенны вычислим по формуле

^(

Амплитудную ДН турникетной антенны во втором случае (с учётом фазовых ДН излучателей) вычислим по формуле

^+(ф) = |А(ф)+А(ф)| - (4)

Полученные результаты приведены на рис. 8—11, на которых сплошной линией показаны амплитудные ДН ^""(ф), вычисленные без учёта фазовых

ДН по формуле (3), а пунктирной - амплитудные ДН /г+(ф), вычисленные с учётом фазовых ДН щелевого излучателя по формуле (4).

Как показали результаты численных исследований, при ЫХ<1 амплитудные ДН |я⁺(ф)| и |/” (ф)| практически совпадают друг с другом (рис. 8). Амплитудная ДН А⁺(ф) поворачивается против хода часовой стрелки (рис. 9, 10). В промежутке 2 <  L / X < 3 расхождения диаграмм направленности становятся значительными.

При значении 3 <  L / X < 4 амплитудные ДН турникетной антенны, вычисленные с учётом и без учёта фазовых ДН излучателей, по форме практически совпадают. Отличие заключается в том, что амплитудная ДН, вычисленная с учётом фазовых ДН, повёрнута относительно амплитудной ДН, вычисленной без учёта фазовых ДН. На рис. 12 и 13 представлены амплитудные и фазовые ДН турникетной антенны при разности фаз напряжений ±90°. Как видно из графика на рис. 13, фазовая ДН турникетной антенны с излучателями в виде щелей на ленте ограниченных размеров отличается от линейной зависимости.

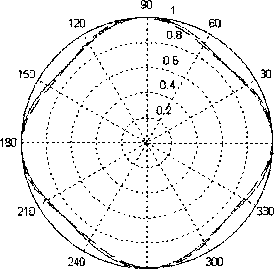
Рис. 8. Амплитудная ДН турникетной антенны, £/Х = 1:

---амплитудная ДН /""(ф);

— — амплитудная ДН К+(ф)

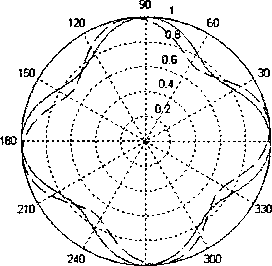
Рис. 9. Амплитудная ДН турникетной антенны, L/Х = 1,5: ---амплитудная ДН /^7-(ф);

— — амплитудная ДН ^(ф)

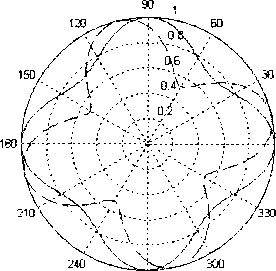
Рис. 10. Амплитудная ДН турникетной антенны, £)Х = 2

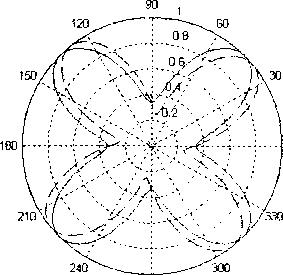
Рис. 11. Амплитудная ДН турникетной антенны, L^X = 3

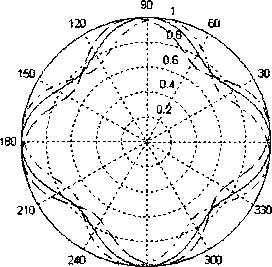
Рис. 12. Амплитудная ДН турникетной антенны: ----- ДН без учёта фазовых ДН излучателей; ---амплитудная ДН, сдвиг по фазе между напряжениями излучателей +90°;

— — диаграмма с разностью фаз между напряжениями излучателей -90°

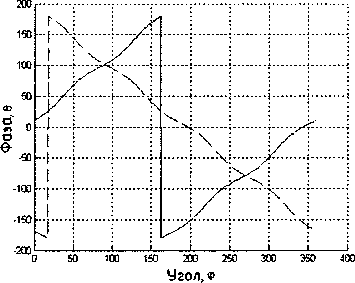
Рис. 13. Фазовая ДН турникетной антенны:

--- ДН при разности фаз между напряжениями излучателей +90°;

— ДН при разности фаз между напряжениями излучателей -90°

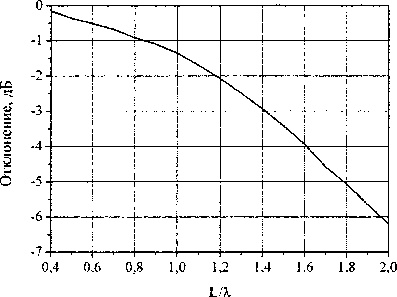
Рис. 14. Зависимость отклонения амплитуды диаграммы направленности от ширины ленты

На рис. 14 приведен график отклонения амплитудной ДН от круга в зависимости от ширины лент, из которых построена турникетная антенна.

Найденная зависимость разворота максимумов ДН от исходного, совпадающего с положением ленты в пространстве, подтверждается данными экспериментов, полученными на макете турникетной антенны, в которой ленты щелевых излучателей были изготовлены из тонкой жести.

Анализ численных экспериментов показал, что отклонения ДН турникетной антенны от круговой ДН не превышают величину ±1,5дБ при отношении периметра ленты к длине волны менее величины 1,4.

Выводы

• 1.    При расчёте ДН щелевой турникетной антенны практически важно учитывать наряду с амплитудными ДН фазовые ДН щелевых излучателей, образующих турникетную антенну.

• 2.    Отклонения ДН турникетной антенны от круговой ДН не превышают величину ±1,5 дБ при отношении периметра ленты к длине волны менее величины 1,4.

• 3.    С ростом отношения ширины ленты к длине волны наблюдается увеличение угла разворота максимумов амплитудных ДН относительно исходного положения максимумов, наблюдаемого при стремлении упомянутого отношения к нулю. Направление разворота ДН определяется опережением (отставанием) по фазе напряжения источников возбуждения щелей.

• 4.    Фазовая ДН турникетной антенны с излучателями в виде щелей на ленте ограниченных размеров отличается от линейной зависимости, характерной для излучателей с ДН в виде косинусоидальной и синусоидальной зависимостью напряжённостей полей от азимутального угла.