Влияние формы и термической массивности тел на эффективность аккумуляционных процессов

Задача определения эффективности аккумуляционных процессов решается с различной степенью точности при расчете требуемой мощности подводимой к агрегатам энергии, при эксплуатации регенеративных теплообменников, при разработке ограждения тепловых агрегатов и в ряде других ситуаций научно-производственного плана. От методики решения этих задач зависит актуальный ресурсо- и энергосберегающий результат эксплуатации металлургических агрегатов.

Постановка задачи и выбор метода решения

В работе [1] отмечены три способа определения расхода теплоты в процессе нагрева тел различной формы и теплофизических свойств. В общем случае при применении закона Фурье расход теплоты определяется интегрированием температурной функции tп по поверхности элемента и по времени процесса нагрева τ. При известной температуре по объему элемента достаточно интегрирования по объему; при известной интенсивности подвода теплоты α (Вт/м2·К) возможен учет температуры окружающей среды. Для одномерных задач температурное поле является функцией только одной координаты η и времени τ, тогда средняя по объему элемента температура tосбр равна n n tосб (т) = -Т I nY-1 t(n,т)dn.                  (1)

n ^Y n= 0

Температурная функция под знаком интеграла определяется дифференциальным уравнением теплопроводности Фурье dt(n,t) л д21(n,t) + y- 1 51(n,t) дт pc dn2 n dn

В приведенных зависимостях фактор формы γ = 1 для пластины, γ = 2 для цилиндра и γ = 3 для шара; λ, ρ, с – теплопроводность, плотность и теплоемкость материала элемента в согласованной системе единиц. Для получения конкретных температурных зависимостей необходимо к уравнению (2) присоединить условия однозначности – геометрические, теплофизические, начальные и граничные, что позволит решить задачу методом разделения переменных. Решение в безразмерных числах подобия имеет вид:

^

®^_ E D i C i exp ( ^-^ 2 Fo ) . (3) i = 1

Здесь Θ = (t0 – tη,τ)/(t0 – tнач) – безразмерная температура (температурный фактор) при нагреве элемента от начальной температуры tнач до температуры tη,τ при температуре окружающей среды t0; μi – корни характеристических уравнений, то есть собственные числа краевой задачи; Fo = λτ/ρc – число Фурье – безразмерное время процесса нагрева. Параметр Di отражает влияние на динамику нагрева формы элемента и числа Bi = αη/λ, а также связанных с Bi посредством характеристических уравнений собственных чисел μi. Параметр Ci отражает влияние формы элемента, числа Bi и без- размерной координаты рассматриваемой точки Н = η/η0; расчетные формулы для определения Di и Ci сведены в таблицу. В зависимостях таблицы, кроме известных тригонометрических функций, также применены табличные функции Бесселя первого рода нулевого порядка J0 и первого порядка J1 аргументов μi или μiR.

Результаты решения задачи

Сходимость ряда (3), а, следовательно, и число слагаемых при заданной точности расчета определяется формой элемента, заданными условиями однозначности и числом Fo. Обычно на практике принимается, что при Fo ≥ Foр можно ограничиться только первым слагаемым ряда (3). Для этих условий:

0 1 = A i exp ( -^ 2 Fo ) ;                        (4)

® cpi = ^ ср exp ( -^ 2 Fo ) ,                      ⁽⁵⁾

где A 1 = D 1 ·C 1 ; A 1 ^cp = D 1 ·C 1 ^cp.

Если в зависимости (3) при i = 1 выделить начальный θнач = t0 – tнач и текущий θ1 = t0 – tη,τ температурные напоры, то при учете только первого слагаемого суммы можно определить

6 1 = А 1 * ⁰ нач ^ех Р ( ^-m 2^Fo )                      ⁽⁶⁾

и логарифмированием выделить постоянную часть и часть, зависящую от времени,

In 0 1 = - m т + In Л 1 0 _нач = - m т + const,       (7)

то, продифференцировав (7) по времени, можно определить темп нагрева m d In 01 дт

- m =

1 д0 1

0 1 дт

Темп нагрева, таким образом, является относительной скоростью снижения температурного напора от начального значения θнач к текущему значению θ1, определяемому по зависимости (6). Причем температурный напор как разность температур между греющей средой и какой-либо обла- стью нагреваемого элемента можно конкретизировать либо относительно поверхности элемента, либо относительно его оси. Следует отметить, что индекс «1» в зависимостях (4)–(8) соответствует первому слагаемому ряда (3), поэтому эти зависимости можно применить к любой области элемента. Область существования этих решений называют областью регулярного режима и обычно наступление этого режима определяют по значению числа Fo ≥ Foр .

Как отмечалось в работе [1], возможно создание таких условий однозначности, при которых температурное поле нагреваемого элемента с самого начала процесса будет подчиняться закономерностям регулярного режима. При этом не конкретизировалось, какие условия необходимо для этого создать, и вопрос ограничивался только рассмотрением начальной температуры. Но, как будет показано ниже, согласование начальной температуры необходимо производить с учетом формы элемента, его теплофизических свойств и условий нагрева.

При распространении закономерностей регулярного режима на начало процесса нагрева при τ → 0 согласно (7) lnθ 1 = ln A 1 θ нач = 0, то есть А 1 θ нач = 1 и θ нач = 1/ А 1 . Это позволяет определить условия начала регулярного режима для любого сечения элемента с координатой η₀ ≥ η ≥ 0; легко заметить, что координата η входит только в выражение для С_i , и при подстановке η = 0 для пластины и цилиндра просто получается cos0 = 1 и J 0 (0) = 1. Для применения этого же приема в случае шарового элемента необходимо разложить в ряд множитель sin(μ _ix )/ x = 1 – x ²/3! + x ⁴/5! – x ⁶/7! , который при η → 0 быстро сходится к единице; эти данные приведены в таблице.

В работе [2] утверждается, что число значимых для точности расчетов членов ряда в (3) зависит от значения Fo, что не вполне корректно, так как необходимо учитывать и значение числа Bi. Сам метод решения дифференциального уравнения теплопроводности разделением переменных предопределяет введение константы разделения, которая связывает пространственные температурные поля с их изменением во времени. Зависимости, выведенные выше для начальных температур-

Расчетные формулы для определения безразмерных параметров

Пластина, η≡ х, μi = Bi·ctgμi Цилиндр, η≡ r, μi = Bi·J0(μi)/J1(μi) Шар, η≡ r, μi =(1– Bi)·tgμi Величина Di 2sinμi/(μi + sinμicosμi) 2J1(μi)/μi[J02(μi) + J12(μi)] 2(sinμi – μicosμi)/(μi – sinμicosμi) Величина Сi cos(μiX), где Х = х/х0 J0(μiR), где R = r/r0 sin(μiR)/μiR Величина Ссрi sin(μi)/μi 2J1(μi)/μi 3Bi/μi θ пов при η = 1 (μ1 + sinμ1cosμ1)/2sinμ1cosμ1 μ1[J02(μ1)+ J12(μ1)]/[2J1(μ1)·J0(μ1)] μ1(μ1 – sinμ1cosμ1)/2sinμ1(sinμ1 – μ1cosμ1) θ ось при η=0 (μ1 + sinμ1cosμ1)/2sinμ1 μ1[J02(μ1) + J12(μ1)]/2J1(μ1) (μ1 – sinμ1cosμ1)/2(sinμ1 – μ1cosμ1) Di и μi при Bi≥100 μi =(i –0,5)π; Di =4(–1)i+1/[π(2i – 1)] μi =BiJ0(μi)/J1(μi); Di =2/[μiJ1(μi)] μi =iπ; i = 1, 2, 3, … Di =2(–1)i+1 Biр при m Ho·tg(Ho) HoJ1(Ho)/J0(Ho) 1 – Ho·ctg(Ho) ных напоров, согласованных с параметрами регулярного режима, включают в качестве основного аргумента собственные числа краевой задачи μ, которые зависят от Bi.

Если применить предельный переход для Bi → 0, μ → 0, то можно определить, что D 1 → 1 и C 1 → 1, а все слагаемые ряда (3) с i >  1 стремятся к нулю; характеристические уравнения для Bi → 0 дают μ²₁ = γBi, где γ = 1, 2, 3. Тогда решение уравнения (3) упрощается

0 = exp ( —у BiFo ) , (9) где BiFo = ατ/ρη₀ c = τ/τ₁. Выражение α/ρη₀ с – мера тепловой инерции термически тонкого тела, а τ 1 = ρη 0 с /α – постоянная времени термически тонкого элемента с плотностью ρ, кг/м³, массовой теплоемкостью с , Дж/кг·К, и полутолщиной η₀, м. Постоянная времени (термин из теории колебаний) переходного процесса изменения температурного поля элемента численно равна отрезку времени, за который начальный температурный напор снизится в е = 2,72 раза и составит 0,368 θ нач .

Для другой области Bi ≥ 100, то есть области термически массивных элементов, аналогичных простых зависимостей найти не удается. Определенные для этой области собственные числа краевой задачи μ i и коэффициенты начальных условий D i приведены в таблице. Фактически при Bi ≥ 100 процесс переноса теплоты переходит в область граничных условий 1 рода.

В работе [2] предложено определять связь между темпом нагрева в регулярном режиме m и коэффициентом температуропроводности а не по коэффициенту формы, а по соотношениям, связывающим Bi и Fo через число гомохронности Но = ( m η²/ a )^0,5 = ( m τ/Fo)^0,5. Число Но является не параметром, а аргументом рассматриваемой задачи и характеризует сопоставимость различных отрезков времени по температурным полям, полученным в результате нагрева тел различной формы. Это число определяет правила выбора сходственных моментов времени при адаптации температурных полей в регулярном режиме нагрева с темпом m.

В применении к рассматриваемой задаче этот метод не дает возможности описать температурные поля и не определяет пределы наступления регулярного режима по основным характеристикам процесса, но в то же время представляет попытку связать параметры регулярного режима с числами Bi и Fo или Но. Определив связь Bi и Fo для конкретной задачи, можно описать общую зависимость θ от этих чисел подобия, но в работе [2] этого нет, как нет и определения расхождений при крайних значениях Bi и Fo.

В работе [3] предлагается для тел с числом Bi ≤ 1 расчет температурного поля вести по формулам для термически тонких тел с введением коэффициентов формы и массивности, что являет- ся достаточно оправданным предложением при расчете нагрева металлических тел, но при нагреве керамических тел число Био может превышать значение 6,0 [4].

Обработав численные значения для функции Но = f (Bi), можно получить аппроксимационную зависимость

Но = 0,9Bi °-³8 exp ( — 0,0455Bi ) .            (10)

Зависимость (10) свидетельствует о том, что связь между Но, а значит и Fo, сложная, экспоненциально-степенная.

В этом отношении более точные данные дают зависимости для различных областей чисел подобия [1], где применена замена переменных и = Bi(Fo)^0,5 и тогда для малых значений и предложена формула для определения относительной поверхности пластины

0 = e erfc ( и ) , (11)

где erfc(u) – табличная функция ошибок, связанная с интегралом вероятности. Для больших значений и рекомендуется формула в виде ряда

0 =    1 ¹

V п к и

—

-2 + — , 2 и ³     )

который быстро сходится при увеличении и > 1,0. Если поставить условием применимости формулы (10) сходимость ряда, то можно определить термин «большие значения и», то есть применимость формулы (11) обеспечивается при значениях и > 1,0. Простой численный анализ показывает, что при реальных минимальных значениях числа Bi > 0,1 предел применимости формулы (11) – это Fo ≥ 100, что редко достигается в процессах металлургической теплотехники. Если принять Bi ≤ 2,0, то Fo ≥ 0,25, что также выходит за пределы заданных параметров.

С учетом этого анализа предлагается расчет температурного поля при нагреве элементов огнеупорной кладки или элементов высокотемпературных регенераторов производить по формулам (3)–(6) для интервала конкретных значений чисел Bi и Fo .

Задачу определения границ регулярного режима в зависимости от Fo и Bi можно рассмотреть в другом аспекте, численно решив задачу определения температурного поля тел при заданной точности расчетов. Если поставить условие θ 1 ≥ 10³·Σθ i , где i = 2, 3, …, n , то определенные по результатам расчетов числа Fo_p будут соответствовать началу регулярного режима, а значит и возможности отбрасывания всех членов ряда, кроме первого, с точностью 0,1 %. Это условие в развернутом виде для пластины выглядит так:

A i cos ( p. 1 X ) exp ( —pA O p ) >

> 1°³ ^ A cos ( p i ^X ) exp ( ^—p ²FO p ) . ⁽¹³⁾

Как показали результаты расчетов, при малых значениях Bip < 0,2 при определении среднемассо- вой температуры пластины Fop возрастает до 0,273 при увеличении Bip до ~ 4,0, а затем плавно снижается до Fop = 0,210 при Bip = 50. Описать такую зависимость степенным многочленом с показателем степени до 8 достоверно не удается, лучше применить аппроксимационную зависимость вида

Fo p = 0,309Bi ⁰’⁸⁴⁹⁵ ■ exp ( - 0,3621Bi _p ) . (14)

При определении границ регулярного режима по температуре поверхности, оси или средней по сечению пластины, а также по аналогичным температурам бесконечного цилиндра или шара, необходимы другие аппроксимации.

На рисунке приведена номограмма для определения количества аккумулированной теплоты на основе регулярного режима для пластины, которая отличается от известных номограмм равномерной шкалой для Bi p и Q отн , а также интервалами изменения этих величин. Эту номограмму можно применить и для бесконечного цилиндра или шара, как это показано ниже. Примененные преобразования позволяют определить по результатам численного анализа аппроксимационные уравнения для коэффициентов перехода от плоской поверхности к цилиндрической и шаровой: k _пл-ц и k _пл-ш.

Qomn

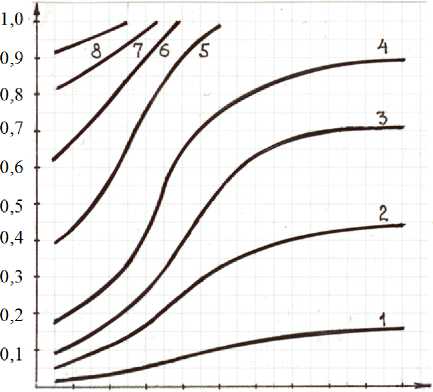
0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 Bi

Зависимость Q _отн от числа Bi при заданном числе Fo : 1 – Fo = 0,1; 2 – Fo = 0,5; 3 – Fo = 1,0; 4 – Fo = 2,0;

5 – Fo = 5,0; 6 – Fo = 10,0; 7 – Fo = 20,0; 8 – Fo = 50,0

Эти коэффициенты определяются по зависимостям kпл-ц = a - bFo; kпл-ш = al + b1/Fo,         (15)

где параметры в уравнениях (15) имеют числовые значения: а = 1,750; 1,519; 1,175 и b = 0,050; 0,104; 0,035 для чисел Bi = 0,10; 1,00; 10,0 соответственно. Далее для перехода от пластины к шару параметры имеют следующие числовые значения а1 = 1,730; 0,835; 0,966 и b1 = 1,47; 0,92; 0,17 для тех же значений чисел Bi.

Выводы

Разработана методика определения количества теплоты, аккумулированной элементом любой формы, и ее практического применения. Производится расчет определяющих чисел подобия Bi и Fo для реальных значений геометрических и теплофизических свойств элементов; по полученным числам подобия с помощью номограммы для плоских элементов определяется относительное количество аккумулированной теплоты Q _отн.

При переходе к элементам другой формы определяются коэффициенты перехода по формулам (12). Полученное значение Q отн , характерное для плоского элемента, умножается на соответствующий коэффициент перехода. Так как полученное значение Q отн = Q акк / Q полн составляет долю от полного количества теплоты, которое было бы аккумулировано при нагреве элемента до температуры греющего теплоносителя, то есть от t _нач до t ₀, то для получения Q _акк необходимо рассчитанное значение Q отн умножить на Q полн = m п C m ( t 0 – t нач ), где m _п – полная масса элемента, кг, С_m – массовая теплоемкость материала элемента, кДж/кг·К. Это также позволяет при известном энергетическом КПД процесса нагрева η эн определить требуемый для нагрева подвод энергии Q тр = Q акк /η эн , кДж, а при известном времени процесса нагрева τ = η²Fo/ a , с, и мощность подводимой энергии, P э = Q тр /τ, кВт.