Влияние формы теплоизолированных объемов на теплопритоки из внешней среды

При проектировании бытовых машин и приборов [1], зданий, сооружений, объектов коммунального назначения [2]; при проектировании сложных технических и других систем жизнедеятельности человека часто ставятся задачи по повышению энергетической эффективности этих объектов [3].

Одним из направлений достижения требований энергетической эффективности эксплуатируемых приборов, зданий и сооружений является совершенствование их теплоизоляции. Для проектирования теплоизоляции различных объектов используются известные методики по расчету теплопритоков через плоские и не плоские ограждения, через однослойные и многослойные стены и другие поверхности.

С целью увеличения сопротивления теплопередаче от внешней среды теплоизолиро ванному объекту для ограждений используются материалы с относительно низкой теплопроводностью и применяются технологии с использованием вакуумирования и инертных газов, обеспечивающие относительно низкую теплопроводность таких теплоизоляций (например, стеклопакеты заполненные аргоном, бытовые холодильники с вакуумированными стенками холодильного шкафа [4] и др.). Проблема снижения теплопритоков в теплоизолированный объект напрямую связана с энергосбережением. Увеличение теплоизолирующих свойств ограждений обеспечивает снижение энергозатрат, необходимых для поддержания рациональных температур в теплоизолированном объеме.

• ¹ Петросов Сергей Петрович - доктор технических наук, профессор, заведующий кафедрой "Технические системы жилищно-коммунального хозяйства и сферы услуг", моб.: +7 928 2133604;

• ² Лемешко Михаил Александрович — кандидат технических наук, профессор кафедры ’’Технические системы жилищно-коммунального хозяйства и сферы услуг", моб.: 8-988-252-85-53, е-mail: lem-mikhail@ya.ru ;

• ⁴ Цоколова Веста Сергеевна - соискатель кафедры "Технические системы жилищно-коммунального хозяйства и сферы услуг”, моб.: +7 938113 72 97.

  
  

  Для минимизации затрат на поддержание рациональных температур в зданиях и сооружениях, в других объектах, важно определить влияние формы этих объектов на тепло-притоки через их ограждения. Важно выяснить: какая форма более рациональна - шарили куб, параллепипед или цилиндр? Важно выяснить существует ли оптимальное соотношение геометрических параметров объектов различной формы, при которых теплопритоки минимальны.

  Для ответа на эти вопросы выполним анализ различных геометрических форм теплоизолированных объектов из условия:

  
  

  Таким образом, теплоэнергетический показатель формы объекта в форме шара зависит от его радиуса и уменьшается с увеличением радиуса по гиперболической зависимости.

  Для сравнения различных форм объектов, будем рассматривать единичный объем, условно равный «1». Например, объекты объемом — 1м . :

  
  

  0,62.

  
  
  
  

  — -> min, ^,

  
  
  
  

  где : S ₃- общая площадь поверхности теплоизолированного объема; V - теплоизолированный объем.

  Это выражение интерпретирует условие минимальной площади поверхности теплоизолированного объема на единицу объема.

  Следует при этом учитывать то, что теплопритоки, например через плоскую стену, определяются по формуле :

  
  

  Теплоэнергетический показатель формы шара единичного объема равен (4):

  Efmin ~ 4,83.

  • 2.    Куб. Куб представляет собой частный случай прямоугольного параллепипе-да, для которого «теплоэнергетический показатель формы» равен:

  S     7   77

  ■ f               h   г ,(6)

  • 1    Го    а   bс

  где a, b, c - длины сторон параллепипеда.

  Для куба:

  
  

  „ _ s₀ _ 6 bf - — -" .

  ⁷ Г_о а

  
  
  
  

  Q = /XT-F-^ ,

  
  
  
  

  где : Q - количество теплоты, Вт; А T - разность температур перед и за ограждением; F- площадь ограждения, м 2; X - коэффициент теплопроводности материала ограждения, Вт/ мтрад; 5 -толщина ограждения, м.

  Таким образом, минимизация площади ограждения (для определенного теплоизолированного объема), обеспечит минимизацию теп-

  
  

  Для единичного объема куба: Ef_min = 6.

  Как видно при сравнении, форма шара характеризуется более низким «теплоэнергетическим показателем формы», что важно при решении задач минимизации теплопритоков через стенки ограждения.

  3. Форма объема - прямоугольный паралле-

  
  

  3.1.

  
  

  лепипед .

  Основание квадрат. В этом случае a = b , тогда:

  
  

  лопритоков через ограждение и, следовательно, минимизацию затрат тепла для поддержания рациональных температур в теплоизолированном объеме.

  Выполним анализ характерных форм теплоизолированных объектов, используя выражение (1). Для сравнения различных форм теплоизолированных объемов по соотношению (1), введем понятие «теплоэнергетический показатель формы» теплоизолированного объема, Ef .

  Ef ⁼ ~ , [ m² /m³], или[m^-1].        (3)

  Рассмотрим типичные формы теплоизолированных объектов .

  • 1.    Шар (sphere).Объем шара равен:

  Т/ — — тгРЗ г splr 2 ~    .

  Площадь поверхности шара:

  ^sph, ~~ 4"V I {^ .

  Теплоэнергетический показатель формы шара равен:

  • ^Ef = 3/R.                        (4)

  
  

  р _ 4

  bf — — —-- г

  ⁷ Го а

  Из условия Kq = а

  £ • _    _

  f — — — ⁷ Г_о

  
  

  2 ' —

  с

  2 .

  
  
  
  
  
  

  Го

  С:         , тогда:

  2a² Го .

  
  
  
  

  Функция (9) содержит сумму гиперболы Е^ = -, и параболы E₂f = 2 а²; следовательно, должно существовать минимальное значение показателя Ef, для каких-ний " a " и "У_о".

  Для единичного объема значение показателя Ef

  
  

  E_f =- + 2а². .

  ¹ а

  
  
  
  

  Находим значения "а", при котором показателя Е^имсст минимальное значение. Вычисляем производную от функции и приравниваем её к нулю : = 4 a -4а² = 0 , 4 a =4а², a =1,

  С э =1.

  а²

  Как видно, для квадратного сечения основания параллелепипеда, теплоэнергетический показатель формы теплоизолированного объема Ef имеет минимальное значение при

  
  

  С.П. Петросов, М.А. Лемешко, В. С. Цоколова

  
  

  а=в=с=\, т.е. при кубической форме единичного объема.

  Из выражения (10) следует, что мини

  
  

  E_f = 8 b -3/й² = 0, Откудай_опт = j| =0,721, где b □пт - значение параметра b при наименьшем

  
  

  мальное значение показателя равно:

  Efmin ~ Т 2а = 4+2=6.          (11)

  Графическая интерпретация формирования показателя ^приведена на рис. 1.

  3.2. Основание прямоугольного параллеле-

  
  

  значснииЕ^.

  Таким образом, для единичного объема

  
  

  ^ ^min

  
  

  получим:

  
  

  пипеда - прямоугольник.

  Используем выражение (6) и рассмотрим некоторые варианты соотношения сторон основания: a =2 b , a =4 b , a =8 b .

  Для каждого варианта определим значение показателя Е^ для единичного объема.

  1) a =2 b .

  Используя выражение (6) получим:

  
  

  з          ~

  Efmin 7   1" 4Ь_Опт ~6,24.

  ^ОПТ

  
  
  
  

  Значение других параметров при минимальном значении показателя: a = 2 b 1,442,с =

  
  

  Гр 2Ь²

  
  

  « 0,962 . 2-0,721²

  
  

  Для единичного объема наименьшее значение показатель формы имеет при еле-

  
  

  дующем соотношении стон прямоугольного

  
  

  г? ___       ___ 1

  ^Ef-V₀-b ⁺ c

  
  
  
  
  

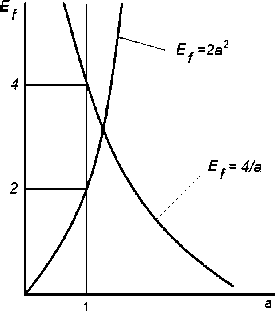
  Рисунок 1 -Формирование показателя £^ для кубической формы

  
  

  параллелепипеда:

  а/b/c =1,44 / 0,721 / 0,962(17)

  2) a =4 b

  Используя выражение (6) получим:

  S 7 57

  /1 о\

  f — - — —- 1--.(18)

  J Ко b с

  
  

  Для постоянного объема У_о=4b 2 c, откуда

  с = -^                       (19)

  4Ь² ,                            (19)

  
  

  Для постоянного объема У_о=2 b 2 c ,откуда

  
  

  с = -^-

  .

  2Ь²

  Подставим значение "с' (12), получим зависимость:

  _3  4Ь^

  — .

  * ь v₀

  
  

  " в выражение

  
  
  
  

  Подставим значение "с" в выражение (18), получим зависимость

  _          пт

  f ь к0 .(20)

  Для единичного объема 7 5

  -Lon

  f               .(21)

  J ь

  Находим условия минимального значения показателя, берем производную зависимости (21):£^-= 16 b -2,5/й²,16 b -2,5/й² = 0, откуда: з /2 5

  ^опт =              ,

  . ^опт

  
  

  Из полученной зависимости следует, что при любом значении параметра " b " увеличение объема снижает теплоэнергетический показатель формы .

  Для единичного объема зависимость пока

  
  

  Другие размеры параллепипеда: a =4^опт ~2,156; с = -§- « 0,86.Размеры и форма параллепипеда характеризуются сле

  
  

  зателя Е^ от параметра " b "имеет вид:

  Е# = — + 4й².               (15)

  J ь

  Как видно, выражения (10) и (15) идентичны, т.е. для этого вида зависимостей суще

  
  

  ствует определенное минимальное значение «теплоэнергетического показателя формы» теплоизолированного объема.

  Определим минимально возможное значение показателя Е^ для единичного объема. Для этого вычисляем производную от функции и приравниваем её к нулю.

  
  

  дующими соотношениями:

  а b/c =2,156/0,539/0,86                (23)

  3) a =8 b .

  Аналогично предыдущим расчетам, находим значение и условия минимального значения «теплоэнергетического показателя формы»:

  „  ,    2^25   -,,₂ г 447g , 2 729 »

  8,177,                                (24)

  а/b/c =3,304/0,413/0,733.             (25)

  Сравнивая соотношения (17), (23), (25) можно сделать вывод, что для единичного объ-

  
  
4. Рассмотрим форму теплоизолированного объема в виде цилиндра (cylinder).Объем цилиндра: V_cyl = tt/?²/i; площадь поверхности цилиндра: S_cyl = 2nRh.C учетом площади оснований цилиндра значение теплоэнергетического показателя формы равно:

ема, с увеличением величины одной из сторон, форма объема приобретает более «вытянутый» вид, все больше отличаясь от формы куба.

При этом минимальное значение «теплоэнергетического показателя формы» увеличивается, как видно при сравнении показателей (11), (16), (22), (24). Так, этот показатель от значения "6" (для куба) возрастает до значения "8,177" (для прямоугольного параллепипеда, для условия: а=8b ), что составляет увеличение показателя на 36,28%. По-видимому, величина теплопритоков в теплоизолированный объем для этого случая будет увеличена примерно на эту же величину.

fmin ^— ^ (^ + _h), (26)

В отличие от формы в виде параллепи педа, для цилиндра нет единственного оптимального значения с минимальным значением теплоэнергетического показателя.

Используя, приведенную выше методику анализа, получим для единичного объема: R и0,553; h =1.

~                   ОПА

I liLLll г/         '                                            \    /

Сделаем обобщение выполненных исследований отношения площади поверхности к объему для теплоизолированного единичного объема. Данные сравнения приведены в таблице 1.

Таблица 1 - Сравнение форм теплоизолированных объектов единичного объема по теплоэнергетическому показателю формы (отношение поверхности объекта к его объему).

Полученные закономерности, характеризуют влияние формы теплоизолированных объемов на теплопритоки из внешней среды.

Рассмотрен вариант этого влияния для единичного объема.

Как видно при сравнении показателей характерных форм теплоизолированных объектов, наиболее рациональными являются объекты шаровидной и цилиндрической формы. Однако объемы реальных теплоизолированных объектов могут быть разными. Из рассмотренных зависимостей (9), (14), (20), и др., очевидно, что увеличение объема теплоизолированного объекта приводит к снижению показателя объема при любых формах и размерах объекта.

Выводы:

• 1.    Форма и размеры изолированного объема существенно влияют на показатель характеризующий отношение площади поверхности к объему теплоизолированного объекта.

• 2.    Наименьшим значением отношения площади поверхности объекта к его объему имеет объект в форме шара.

• 3.    Для единичного объема в форме прямоугольного параллепипеда, минимальное отношение площади к объему имеет куб.

• 4.    Для объекта в форме прямоугольного параллепипеда, для заданного значения длины одного из ребер существует единственное значение длин других ребер, при котором существует минимальное отношение площади поверхности к объему.

• 5.    С относительным увеличением одного из ребер прямоугольного параллепипеда, значение отношения площади к единичному объему увеличивается.