Влияние функции модификации исходного прямолинейного профиля на форму производящей поверхности зуборезного инструмента

Пространственные винтовые зубчатые передачи, в частности червячные передачи с цилиндрическим червяком, широко применяются в большинстве современных машин и машиностроительных изделиях [1–3]. Цилиндрические червячные передачи широко используются в конструкциях различного металлообрабатывающего оборудования (нажимные механизмы прокатных станов, прессы и т. д.), в подъемно-транспортных машинах. Они находят широкое применение в приводах и кинематических цепях различного станочного оборудования [4, 5], т. е. там, где требуется высокая кинематическая точность (делительные устройства станков, механизмы наладки и т. д.)

В цилиндрической червячной передаче - цилиндрический червяк или его винтовая поверхность может быть получена различными технологическими способами, но как бы ни происходило

формообразование рабочих поверхностей элементов червяка, червячное колесо должно быть формообразовано зуборезным инструментом, производящая поверхность которого совпадает с боковой поверхностью витка сопрягаемого червяка [6, 7]. Вследствие этого рабочая поверхность зуба цилиндрического червячного колеса даже при неортогональном расположении осей вращения червячного колеса и сопрягаемого червяка будет являться огибающей однопараметрического семейства поверхностей, что и дает линейный контакт между рабочими поверхностями червяка и червячного колеса. Наличие линейного контакта позволяет передавать большую нагрузку от ведущего червяка на ведомое червячное колесо.

Для качественного изготовления червячного колеса необходимо выполнить проектирование и изготовление точного зуборезного инструмента -червячной фрезы [8, 9], формообразующая (рабо-

Инженерная геометрия и компьютерная графика чая) поверхность которой должна быть эквивалентна рабочей поверхности цилиндрического червяка [10].

Одна из важнейших задач, которая встает при проектировании нового червячного зубчатого зацепления – это проблема заклинивания между контактирующими поверхностями цилиндрического червяка и цилиндрического червячного колеса. Исключение этой проблемы может быть достигнуто путем отвода профилей контактирующих поверхностей вдоль линии контакта внутрь контактируемых элементов червячного зацепления. А если учитывать, что на технические характеристики работы контактирующих поверхностей проектируемой червячной передачи влияют любые нарушения ее геометрических параметров, то главной задачей при изготовлении элементов червячного зацепления является точное определение наладочных параметров применяемого зубообрабатывающего оборудования, которое будет использоваться для формообразования червяка и червячного колеса.

В настоящее время происходит устаревание парка зубообрабатывающего оборудования, применяемого для изготовления элементов червячных передач, т. е. его физический износ, который влечет за собой неизбежное снижения точности кинематических цепей и как следствие снижение точности изготавливаемой продукции. Поэтому для сохранения и улучшения качества выпускаемых червячных передач на достаточно высоком уровне необходимо еще при расчете геометрических параметров червячного зацепления использовать преднамеренную модификацию контактирующих поверхностей, которая позволит уменьшить чувствительность элементов червячной передачи к погрешностям изготовления и их монтажа.

Описание метода, применяемого для преднамеренной модификации сопряженных поверхностей

Возможность заклинивания червячной передачи приводит к необходимости использовать механизм отвода кромок, контактирующих поверхностей, червяка и червячного колеса от их точного профиля, который получается при использовании зуборезного инструмента с исходным прямолинейным профилем. Этот механизм называется отводом профиля, или преднамеренной модификацией рабочей поверхности, которая чаще всего выполняется внутрь контактирующего тела. На рис. 1 показаны рабочие поверхности зуборезного инструмента.

Теоретическая рабочая поверхность – это поверхность, которая получается при использовании для формообразования производящей поверхности зуборезного инструмента с исходным (прямолинейным) профилем, а технологическая рабочая поверхность (модифицированная) получается при использовании для формообразования модифицированного профиля производящей поверхности зуборезного инструмента.

Точка P на рис. 1 называется полюсом зацепления. Это точка, в которой теоретическая и технологические поверхности имеют общую касательную плоскость и в которой должно выполняться равенство:

i = iтеор = iтехн , где i – передаточное число червячной передачи; i – теоретическое передаточное число (точной) боковой поверхности; i    – технологическое передаточное число (реальной) боковой поверхности.

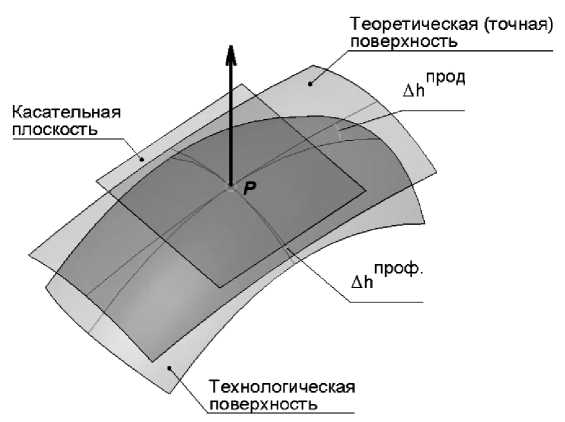
Рис. 1. Боковая производящая поверхность: A h ^прод и A h проф - величины продольного и профильного отклонения поверхностей

Рязанов С.А., Решетников М.К.

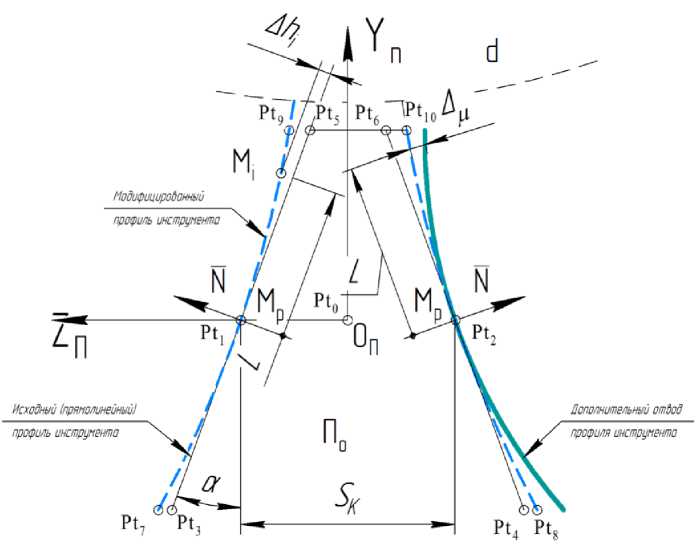
Рис. 2. Исходный осевой профиль обобщенной производящей поверхности

Для формообразования модифицированной производящей поверхности зуборезного инструмента необходимо выполнить преднамеренный отвод исходного (прямолинейного) профиля его рабочей поверхности [11], т. е. получить его модифицированный профиль производящей поверхности П о (Рис. 2).

Модифицированный осевой профиль П o можно задать отводом Ац от исходного прямолинейного профиля производящей поверхности в направлении нормали N в средней расчетной точке профиля M_P . Внесение преднамеренной профильной модификации рабочей поверхности зуборезного инструмента возможно как в табличной форме, так и аналитически в виде функции Ац i = f ( L ) .

Рассмотрим формирование модифицированного осевого сечения рабочей поверхности зуборезного инструмента при помощи квадратичной функции [12-14]:

Ац = ( ц- L ² ) /2, (1) где Ац - величина отвода от линейного осевого сечения в текущей точке линейного профиля; ц - коэффициент, который позволяет влиять на кривизну модифицированного сечения производящей поверхности зуборезного инструмента; L - величина, которая задает шаг вдоль исходного сечения теоретической производящей поверхности зуборезного инструмента.

Для выполнения расчета координат точек, задающих модифицированный профиль зуборезного инструмента, необходимо определить длины левого и правого исходных профилей производящей поверхности (рис. 3).

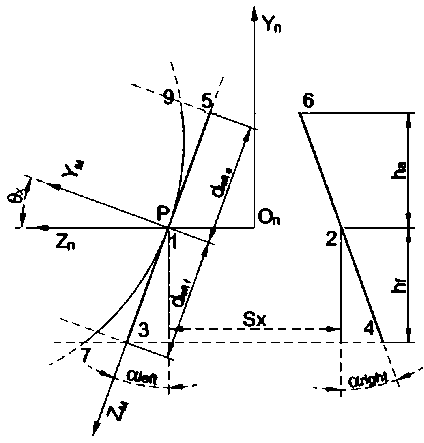
Рис. 3. Аналитическая модель модифицированного осевого сечения зуборезного инструмента

На рис. 3 точки 3 и 4 задают пересечение исходного теоретического профиля производящей поверхности зуборезного инструмента с воображаемой линией, которая задает величину расстояния hj до впадины рабочей поверхности.

Инженерная геометрия и компьютерная графика

Величина h показывает расстояние до делительной окружности. Точки 5 и 6 задают высоту вершин рабочей поверхности на расстоянии h от делительной окружности. Точки 7 и 9 задают пересечение модифицированного профиля производящей поверхности с воображаемой линией впадины и высотой рабочей поверхности соответственно.

Расстояние между точками 1 и 5, 1 и 3, 3 и 5 (рис. 3) в системе координат Y O Z  модифицирован ного профиля производящей поверхности определяется по формулам:

distl 5 = Vh2 " (t g2(aleft > + 1) = —ha—; ,

_                                 co ^s( a left )

hf dist1 3 = Jh 2 • (t g2(a left) + 1) =---------- .(3)

_ ^V                           Co ^s( a left )

Следовательно, полное расстояние (4) между точкой 3 (выражение (2)) и точкой 5 (выражение (3)) рассчитывается по формуле:

dist3 5 = 4 h2 ■ (tg2(aleft) +1) + Jh2 ■ (tg2(aleft) +1) = h     + —ha— .(4)

_ ^V                          V                          _co ^{s( a} left )   _co ^s( _a left )

Аналогично вычисляются расстояния между точками 2 и 4 (выражение (5), 2 и 6 (выражение (6)):

dist2 4 = 4h2 •(t g2(aright) + 1) = —hf,(5)

_    ^{V                         cos( a} right )

dist2 6 = Vha •(t g2 (aright)+1) = —7^.

_    ^{V                         cos( a} right )

Следовательно, полное расстояние между точками 4 и 6 рассчитывается по формуле:

dist4 6 = 4h2 •(t g2(aright)+1) + 4ha •(t g2(aright)+1) = —,—;+—h,

_ V                         V                         cos(aright) cos(aright)

где h и h – высота головки и ножки исходного профиля производящей поверхности зуборезного инст- румента соответственно.

Для вычисления координат крайних точек модифицированного осевого сечения производящей поверхности зуборезного инструмента необходимо получить уравнения прямых, которые проходят через точки 3-7 и 5-9 для левого и точки 4-8 и 6-10 правого модифицированных профилей производящей поверхности в системе координат для левого и правого профиля соответственно (рис. 3).

Эти уравнения будут выглядеть следующим образом:

м     cos(aleft) zM_ hf yleft37    sin(aleft) Z sin(aleft) ,

M        cos( a left )    м y left59 =                Z + 59       sm( a left )	ha sin( a left ) ,	(8)
e      cos( a nght )   e	h f	(9)
> right 48     si n( a right ) "	sin( a right ) ,
м            cos( a right )    м right 6_10       sin( a right )	h +------ a ----- . sin( a right )	(10)

Совместно решая каждое из уравнений (7)–(10) и уравнение (1), которое задает функцию преднамеренной модификации исходного прямолинейного сечения рабочей поверхности зуборезного инструмента, можно определить координаты крайних точек 7–10 модифицированного профиля производящей поверхности в системе координат модифицированного профиля Y_M O_M Z_M :

1   ^- cos ^{( a} left ) ⁺ ^cos ^{2 ( a} left ) ^{- 4} • sin ^{( a} left ) •Ц^ h f

• 2                    sin(aleft) •Ц

1   ^{- cos( a} left ) ⁺ 4 c ^OS 2 ^{( a} left ) ^{+ 4} • sin ^{( a} left ) 'Ц^ h a

• 2                      sin(aleft ) •Ц

Рязанов С.А., Решетников М.К.

1 ^{cos( a} right ) - 4 c ^os 2 ^{( a} right ) - ⁴ ■ ^{sin( a} right ) ■ ^ ■ hf .

2                      sin ⁽ a _right ) ■ц                      ;

_ 1 ^{cos( a} right ) ^- 4 ^cos 2 ^{( a} right ) + ⁴ ■ sin ^{( a} right ) ‘ Ц ‘ h a

2                   sin a right ) ■ц

Уравнения (11)–(14) позволяют определить координаты крайних точек 7, 9, 8 и 10 для модифицированного профиля производящей поверхности, заданного уравнением в квадратичной форме (1).

Аналогично выполним внесение преднамеренного отвода рабочей поверхности зуборезного инстру-

мента при помощи уравнения окружности, которое зададим в виде выражения:

(x - a )2 + (y - b )2 = r2,

где x и y – координаты точки, которая принадлежит модифицированному производящему профилю зуборезного инструмента; a и b – координаты центра окружности; r – радиус окружности.

Для вычисления координат точек модифицированного профиля производящей поверхности зуборезного инструмента запишем уравнение окружности (15) в виде функции y ( x ) :

y (x) = b - V - a 2 + 2 ax + r 2 - x2

Решая совместно каждое из уравнений (7)–(10) и уравнение (16), определим выражения, которые задают координаты крайних точек 7–10 модифицированного профиля производящей поверхности в подвиж-

ной системе координат:

V - b ² + r ² ■ sin( a left ) - a ■ sin( a left ) - h f ^{cos( a} left )

_ У-b2 + r 2 ■ sin(aleft) + a ■ sin(aleft) - ha . cos(aleft)                    ’

4 ^{- b 2 + r 2} ■ si ^{n( a} right ) ^- a ■ si ^{n( a} right ) ^- h f ^;

^{cos( a} right )

V-b2 + r2 ■ sin(aright)+ a ■ sin(aright)- ha cos(aright)

Матричное выражение для перехода от системы координат левого профиля производящей поверхности Y M O M Z M в систему координат S_on ( O_nx_ny_nz_n ) записывается в виде:

^Mм _ left

1	0	0	0
0	cos( 9 x )	- sin( 6 x )	0
0	sin( 6 x )	cos( 6 x )	A z
0	0	0	1

где 0_Х - угол поворота неподвижной системы координат, в которой выполняется расчет координат точек принадлежащих левому модифицированному профилю производящей поверхности; A z - смещение системы координат модифицированного профиля, A z = s /2 .

Координаты точек, принадлежащих сечению производящей поверхности зуборезного инструмента, зададим в виде матричного выражения:

R M^Son ) = x M   У м   Zm  1 T ,                                   (22)

где x_м , y_м , z_м – координаты точки сечения в системе координат модифицированного профиля Y_M O_M Z_M по каждой из осей;

Для получения уравнений в координатной форме выполним умножение матриц (21) и (22):

( Sи )

^rmX = x m ;

• R Mr ) = У т ■ c ^os( 6 x ) ^- z m ■ ^sin( 6 x );

RMSY) = Ут ■ sin(6x ) + zm ■ cos(6x ) + A z.

Инженерная геометрия и компьютерная графика

Подставляя в систему уравнений (23) уравнение (1), получаем систему уравнений для модифицированной левой производящей поверхности зуборезного инструмента при помощи уравнения параболы:

( Sи ) ^RмX

= 0;

R MX ⁾ = 0;

• R MY ) = cos( 9 х ) ■ ( a + V" b ² + r ² ) + z - sin( 9 , );      (29)

R MY ) = ^{sin( 9} х ) ■ ( a ⁺ 4 ^{- b 2} + ^{r 2} ) - Z ^{- cos( 9} х ) ^{- A} Z.

• RMSY) = и- z2 ■ cos(9 х)-z sin(9 х);

RMSY) = и ■ z2 ■ sin(6 х)+zcos(9 х)+A z.

Подставив в систему уравнений (23) уравнение (16), получаем систему уравнений для модифицированной левой производящей поверхности зуборезного инструмента при помощи уравнения окружности:

R MX ) = 0;

• R Y ) = cos ⁽ 9 х ) ■ ( a + V^- b ² + r ² ) ^- z ^{- sin( 9} х );      (25)

R mY ) = sin( 9 _х ) ■ ( a + V— b ² + r ² ) + z cos( 9 _х ) + A z.

Аналогично, можно получить матрицу для перехода от системы координат правого модифицированного профиля производящей поверхности в систему координат 8 оП ( O_nx_ny_nz_n ) :

M м _right

0	0	0
cos( 9 х )	sin( 9 х )	0
sin( 9 х )	- cos( 9 х )	-A z
0	0	1

Умножая матрицы (26) и (22), получаем матрицу преобразования координат для правого модифицированного профиля заданной квадратичной формой:

R Mx ) = ^хт ;

• R S ) = У т ■ cos( 9 х ) + z m ■ sin( 9 _х );          (27)

RMy ) = Ут ■ sin(9х ) - zт ■ cos(9х ) -A z.

Основные результаты и их анализ

В табл. 1 показаны рассчитанные координаты точек осевого сечения модифицированной производящей поверхности зуборезного инструмента при помощи функции, описывающей параболу, (1), а в табл. 2, с помощью функции, описывающей окружность, (16).

Выполняя расчеты координат точек профиля при помощи системы уравнений (29), получаем осевое сечение модифицированной производящей поверхности (рис. 5) при помощи уравнения окружности.

Внесение профильной модификации рабочей поверхности зуборезного инструмента позволяет получить виртуальный эквивалент поверхности модифицированного зуборезного инструмента. Анализ кривизны рабочих поверхностей при помощи разных функций ее модификации (рис. 5), позволяющих выполнить модификацию исходного прямолинейного сечения производящей поверхности, показывает, что для симметричного относительно полюса зацепления отвода профиля от его прямолинейного сечения производящей поверхности можно использовать квадратичную зависимость, представленную выражением (1). Расчет координат точек отвода профиля от прямолинейного при помощи выражения (15) можно использовать в случаях, если требуется разный по величине отвод на ножке и головке производящей поверхности.

Подставив в формулу (27) уравнение, модифицирующее профиль (1), получаем параметрическую форму модифицированной правой произво-

дящей поверхности:

_R ( Sи ) мX

= ^хт ;

• rMsf ) = и ■ z2 ■ cos(9 х)+z- sin(9 х);

RMy ) = и ■ z2 ■ sin(9х ) - z cos(9х ) - A z.

Выполнив расчеты координат точек модифицированного профиля зуборезного инструмента [15-17] по формулам (24) и (28), получаем осевое сечение модифицированной производящей поверхности (рис. 4) для левого и правого профилей производящей поверхности соответственно.

Подставив в формулу (27) уравнение (16), получаем параметрическую форму модифицированной правой производящей поверхности зуборезного инструмента:

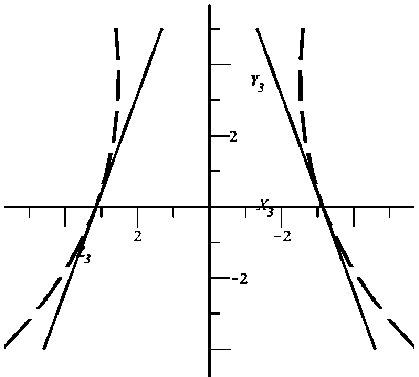
Рис. 4. Модифицированный осевой профиль обобщенной производящей поверхности

Таблица 1

Координаты точек модифицированного осевого сечения производящей поверхности, полученной при помощи квадратичной функции

№ п/п	Z M , мм	YМ , мм	Y , мм	Z , мм
1	–4,886370042	1,193830610	4,999999988	2,592189489
2	–3,909096034	0,764051590	3,934669732	2,522576711
3	–2,931822025	0,429779019	2,902004605	2,542710639
4	–1,954548017	0,191012898	1,902004608	2,652591272
5	–0,9772740080	0,047753224	9346697386	2,852218611
6	0,0000000000	0,000000000	0,000000000	3,141592654
7	0,9300501734	0,043249666	–,8591690281	3,500329939
8	1,860100347	0,172998665	–1,688753542	3,940350009
9	2,790150520	0,389246996	–2,488753542	4,461652863
10	3,720200694	0,691994660	–3,259169029	5,064238503
11	4,650250867	1,081241656	–4,000000000	5,748106926

Таблица 2

Координаты точек модифицированного осевого сечения производящей поверхности, полученной при помощи функции, описывающей окружность

№ п/п	Z M , мм	Y М , мм	Y П , мм	Z П , мм
1	–4,886370042	0,427725530	–4,445395125	–5,214760158
2	–3,909096034	0,272987630	–3,579981430	–4,735106700
3	–2,931822025	0,153227720	–2,702604556	–4,288321800
4	–1,954548017	0,067997900	–1,813417698	–3,873984571
5	–0,9772740080	0,016984050	–0,912528287	–3,491799836
6	0,0000000000	0,000000000	0,000000000	–3,141592654
7	0,9300501734	0,015381860	0,879222191	–2,837950981
8	1,860100347	0,061578050	1,768983503	–2,563265307
9	2,790150520	0,138741140	2,669336120	–2,317679000
10	3,720200694	0,247128280	3,580367991	–2,101433702
11	4,650250867	0.387105490	4.502204301	–1.914873360

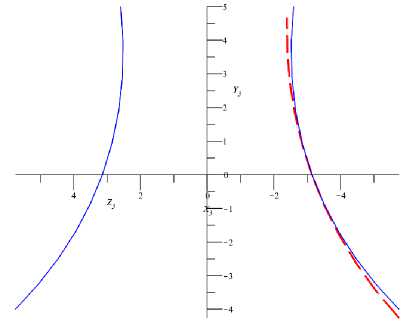
Рис. 5. Влияние алгоритма модификации на отвод производящего контура рабочей поверхности зуборезного инструмента

Заключение

Создание эффективных методов описания геометрических элементов машиностроительных изделий с привлечением современных средств компьютерного геометрического моделирования позволяет значительно сократить сроки и повысить точность их изготовления.

Внесение преднамеренного профильного отвода производящей поверхности от исходного прямолинейного профиля влечет за собой модификацию сопряженной рабочей поверхности полученного изделия, что в итоге приведет к улучшению рабочих характеристик в зоне контакта червячной передачи. Применение цифрового про-

Инженерная геометрия и компьютерная графика тотипа модифицированной производящей поверхности позволяет выполнять получение виртуального изделия, используемого в зубчатой передаче.