Влияние гармонических составляющих сигнала на форму петли гистерезиса

Известно, что гистерезис обусловлен запаздыванием отклика системы любой природы на внешнее воздействие. Это явление хорошо известно в физике, технике, экономике, социологии, биологии и других отраслях науки. Любая система на внешнее воздействие реагирует не мгновенно, но петли гистерезиса представляют интерес, прежде всего, для систем с нелинейным откликом. В физике гистерезисные зависимости чаще всего применяются для изучения свойств нелинейных материалов: ферромагнетиков и диэлектриков. Нас интересует физическое применение петли гистерезиса.

В настоящее время имеется достаточно много математических моделей гистерезисных зависимостей [1-3]. Имеющиеся модели гистерезиса построены на решении нелинейных дифференциальных уравнений, либо на введении нелинейных гистерезисных членов в линейные уравнения. Подобным образом построены модели Прайсаха, Джилеса-Атертона, Хаузера и другие. Использование нелинейных уравнений приводит к значительному усложнению модели из-за того, что трудно получить универсальное решение и интерпретировать результаты. В случае линейного уравнения сложно найти достаточно простую добавку, которая не приводила бы к значительным математическим трудностям и позволяла бы воспроизвести параметры петли. Если гистерезисный член прост, как, например, функция Прайсаха и подобные ей [3], то здесь требуется задание параметров петли, т.е. такой подход позволяет получить только полуэмпиричес-кие модели.

Реальные системы с запаздыванием могут описываться петлями гистерезиса самой разно-

Лукичёв Александр Александрович, кандидат физикоматематических наук, старший научный сотрудник лаборатории керамического материаловедения.

образной формы. Исчерпывающей классификации петель гистерезиса в настоящее время нет. В работе [4], например, приведено 6 различных типов петель, которые далеко не отражают разнообразие гистерезиса для реальных материалов.

В работе [5] предложен метод построения петли гистерезиса, как параметрической зависимости функции отклика системы от функции внешнего воздействия Y(t)=f(X(t)). При этом считается, что система близка к линейной и с достаточной точностью описывается линейным уравнением, решение которого известно. Нелинейные явления учитываются введением в линейное решение дополнительной нелинейной функции. Если известен вид нелинейной функции, этот метод позволяет легко воспроизвести классическую петлю гистерезиса, описывающую насыщение магнитной или диэлектрической проницаемости. В [5] авторы рассмотрели единственный вид нелинейности – ограничение амплитуды в результате насыщения физического параметра материала под действием внешнего поля, или нелинейность типа “насыщение”. В настоящей работе рассматривается влияние произвольных нелинейных искажений на форму петли. Рассматриваем колебания близкие к гармоническим, для учёта нелинейности вводится сумма гармонических составляющих порядка выше первого. Природу нелинейности здесь не рассматриваем.

Любую систему с гистерезисом можно представить в виде очевидной блок-схемы, показанной на рис. 1. Имеется входное воздействие X(t) , на которое система, с передаточной функцией W( a , X ( t )) , даёт отклик Y ( t ) = W • X(t ) . Передаточная функция определяется свойствами системы и зависит от амплитуды и частоты входного сигнала, а так же от свойств самой системы. Петля гистерезиса представляет собой параметрическую зависимость Y(t)=f(X(t)).

Рис. 1. Блок-схема системы с гистерезисом

Будем рассматривать реакцию системы, близкой к линейной, на гармоническую входную функцию вида

X ( t ) = X ₀ • sin( to - t ) . (1)

Здесь X₀ – амплитуда входного воздействия, t – время. Отклик системы в общем случае будет состоять из основной гармоники на частоте входного сигнала и суммы гармонических составляющих с более высокими частотами, т.е. функция отклика может быть представлена в виде ряда Фурье:

Y(t) = Y + Eancos(n-to-1^Фап) + Ebn • sin(n-to- t+фьп) ,(2) nn где Y0 – постоянная составляющая, n (1, 2, 3…) – номер гармоники, an, bn –амплитудные коэффициенты, фап, фьп — отставание по фазе составляющих n-й гармоники. Для простоты будем считать фа1 = фЬ1 = фап = фЬп = ф •

Используя метод построения петли гистерезиса предложенный в [5] будем рассматривать влияние на форму петли каждой гармонической составляющей по отдельности. Рассмотрим влияние второй гармоники. Функцию отклика, учитывающую вторую гармонику представим в виде: Y ( t ) = Y i • sin( to - 1 + ф ) + к_а cos(2 to - t + ф ) + к ь • sin(2 to - t + ф ) , (3) здесь Y₁ –амплитуда первой гармоники, k_a, k_b – амплитудные коэффициенты. Далее принимаем Y 1 = 1.

На рис. 2 показаны петли гистерезиса для различных сочетаний амплитудных коэффициентов k_a, k_b и при различных фазах. В работе [5] рассматривался гистерезис для линейного осциллятора и в качестве характеристических точек были выбраны резонансная частота и частоты выше и ниже резонансной. Выбранным значениям частоты соответствуют фазы: ниже точки резонанса фф <  я /2 , на резонансной частоте ф 2 = я /2 и частоте, выше резонансной, ф 3 >  я /2 [6]. Ниже мы будем использовать эти значения фазы для определения характеристических точек. Сигнал отклика запаздывает по отношению к входному воздействию, поэтому фаза отклика всегда отрицательна. Здесь и далее для удобства мы указываем абсолютное значение фазы.

Петли гистерезиса для сигнала отклика с косинусоидальной второй гармоникой ( k_a=± 0,1; k_b =0) показаны на рис. 2а и 2б. Значение коэффициента k_a=± 0,1 выбираем произвольно, поскольку нас интересует только форма петли. Как

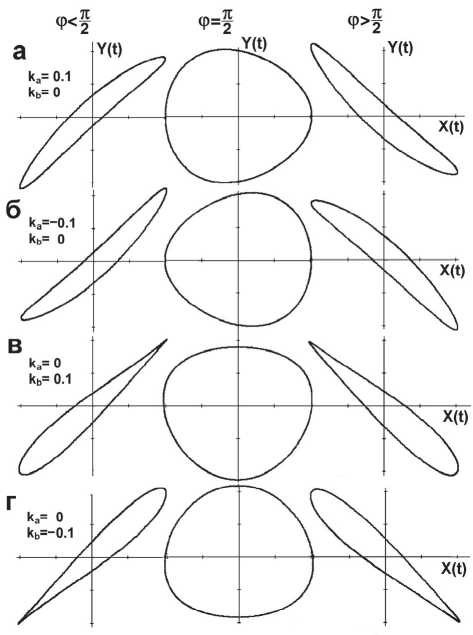
Рис. 2. Влияние второй косинусоидальной и синусоидальной гармоник на форму петли гистерезиса при различных фазах функции отклика видно из рисунков, косинусоидальная вторая гармоника приводит к боковым петлям типа “месяц”. В точке резонанса ( ф = я /2 ) петля превращается в эллипс, несимметричный относительно 0Y, или в треугольник с существенно скруглёнными углами. Синусоидальная вторая гармоника (к==0; kb=±0,1) для точек ф1 < я/2 , ф3 > я/2 приводит к петле типа “капля”, острый конец которой может быть направлен как вниз, так и вверх (рис. 2в, 2г), в зависимости от знака коэффициента kb. В точке ф = я /2 петля превращается в несимметричный эллипс, повёрнутый на угол р относительно эллиса для косинусоидальной гармоники. Для всех графиков на рис. 2 правую петлю можно получить из левой поворотом на угол я /2 •

Рассмотрим влияние третьей гармоники. Функцию отклика, учитывающую третью гармонику представим виде:

Y ( t ) = I ) - sin( to - 1 + ф ) + к_а cos(3 to - 1 + ф ) + к_ь • sin(3 to - 1 + ф ) • (4)

На рис. 3 показаны петли гистерезиса для различных сочетаний амплитудных коэффициентов в характеристических точках. Петли гистерезиса для сигнала отклика с косинусоидальной второй гармоникой ( k_a=± 0,1 ; k_b= 0) показаны на рис. 3а, 3б. Как видно из рисунков, для косинусоидальной гармоники на частотах ниже и выше резонансной получаются петли типа “веретено” и “гантель”. При ф = я /2 петля превра-

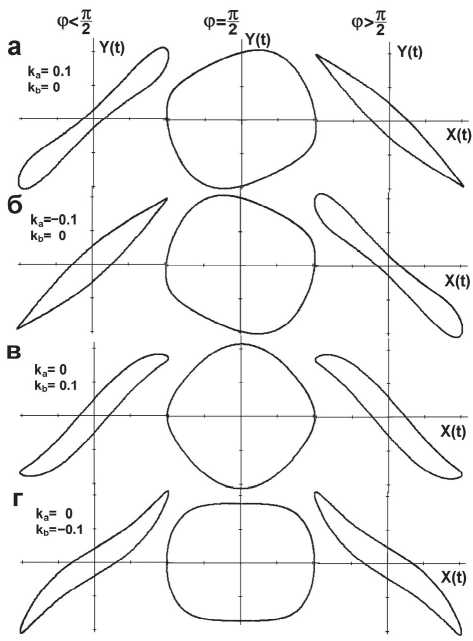
Рис. 3. Влияние третьей косинусоидальной и синусоидальной гармоник на форму петли гистерезиса при различных фазах функции отклика щается в фигуру, которую можно назвать как скруглённый прямоугольник. Петля несимметрична относительно осей координат.

Синусоидальная третья гармоника ( k_a =0; k_b =±0,1) приводит к боковым петлям, близким по форме к классической петле с нелинейностью типа “насыщение”. В точке ф = к /2 для положительной гармоники петля превращается в скруглённый ромб, для отрицательной гармоники в скруглённый прямоугольник.

Аналогично, используя соотношение

Y ( t ) = Y • sin( № 1 + ф ) + k a cos(4 ® - 1 + ф ) + k b • sin(4 ® • t + ф ) ,(5) находим петли для четвёртой гармоники. Как видно из рис. 4, четвёртая гармоника приводит к существенному искажению петель. Боковые петли для косинусоидальной гармоники представляют собой сильно искажённые петли типа “насыщение” (“туфля”), для синусоидальной – комбинация из петель второго и третьего порядка. Центральная петля имеет вид скруглённого пятиугольника.

Учёт гармоник более высокого порядка представляется нецелесообразным, поскольку на практике амплитуда этих гармоник, как правило, невелика.

Анализ графиков на рис. 2-4 позволяет сделать следующие выводы. Количество углов у центральной петли на единицу превышает номер

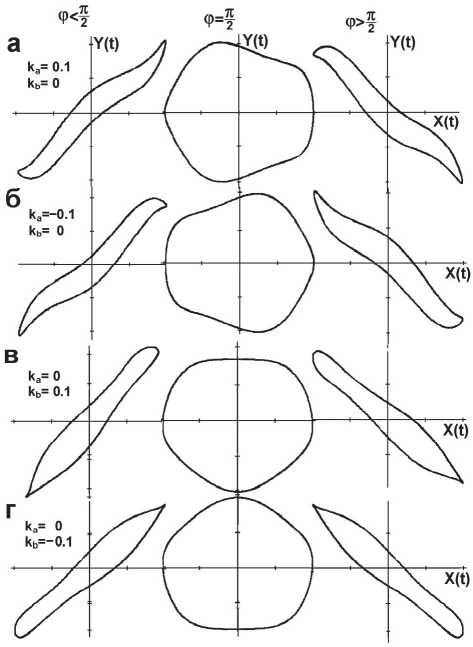
Рис. 4. Влияние четвертой косинусоидальной и синусоидальной гармоник на форму петли гистерезиса при различных фазах функции отклика гармоники. Для гармоник порядка выше 2 у боковых петель количество точек перегиба на единицу меньше номера гармоники (рис. 3, рис. 4). Боковые остроконечные петли с острыми концами наблюдаются для чётных синусоидальных гармоник и нечётных косинусоидальных. Центральные петли, несимметричные относительно обеих координатных осей, наблюдаются для нечётных гармоник, кроме первой.

Для заторможенных колебаний фаза изменяется в пределах 0 <  ф <  к /2 [6]. В этом случае, изменение формы сводится к уширению малофазной (левой) петли с одновременным снижением амплитуды отклика [6]. К сожалению, в этом случае затруднено определение вида искажений, поскольку невозможно построить центральную петлю.

Для подтверждения полученных выше теоретических результатов были сняты петли гистерезиса для произвольного стального стрежня в линейном (ненасыщенном) режиме в диапазоне частот 20 Гц – 500 кГц. Частотная зависимость магнитной проницаемости стали имеет довольно сложный вид с большим количеством резонансных пиков. На низких частотах для большинства пиков наблюдается линейный гистерезис с петлями, близкими к правильному эллипсу. На частотах выше 100 кГц получен пик. у которого заметно влияние нелинейных искажений.

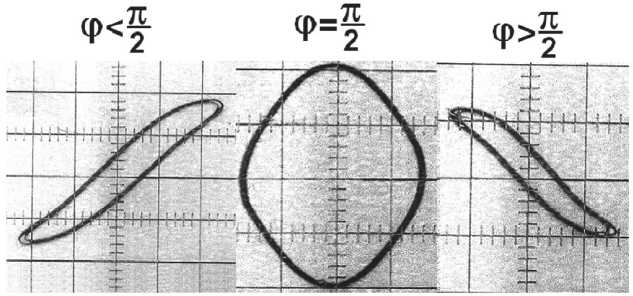
Рис. 5. Петли гистерезиса для намагниченности стали в характеристических точках

На рис. 5 показаны петли гистерезиса для пика с резонансной частотой 130 кГц. Форма петли соответствует показанной на рис. 3в, т.е. третьей положительной синусоидальной гармонике. Для боковых петель заметна незначительная клино-видность вниз. Это означает, что также присутствует первая положительная синусоидальная гармоника (рис. 2в), но её амплитуда невелика.

Форма петли существенно зависит от амплитуды тока намагничивания, при низких токах петля превращается в правильный эллипс.

В настоящей работе автор не ставил целью найти всё многообразие петель гистерезиса, здесь в большей степени показан метод анализа петель гистерезиса,

ЗАКЛЮЧЕНИЕ

Выше было рассмотрено влияние гармоник совпадающих по фазе с основной. Но фаза гармоники может быть любой. Очевидно, что форма петли зависит от фазы. Постепенное увеличение фазового сдвига для косинусоидальной положительной функции приводит к постепенной трансформации формы петли от показанной на рис. 3а к 3г, далее к 3б и 3в. Здесь получены петли только синусоидальной входной функции, очевидно, что для косинусоидальной функции будет получен тот же набор петель. Если одновременно имеются косинуоидальная и синусоидальная гармони- ки, то форма петель будет либо близка к показанным на рис. 2-4, либо будет иметь вид комбинации из каких либо двух петель, показанных на рисунках. Комбинация левых петель, показанных на рис. 3а и 3в даёт классическую петлю гистерезиса, свойственную материалам с нелинейностью типа “насыщение”. Для того, чтобы определить тип нелинейности необходимо измерение гистерезиса в особой точке ф = я /2 .