Влияние геометрических и физических параметров на резонансные частоты ультразвуковых колебаний системы упругих и пьезоэлектрических элементов

Введение. Ультразвуковые скальпели позволяют проводить рассечение и коагуляцию тканей с целью остановки кровотечения [1–4]. Конструктивно такие приборы состоят из цепочки упругих и пьезокерамических (или магнитострикционных) элементов, собранных в единую систему, создающую максимальные продольные колебания режущему элементу на частотах от 20 до 50 КГц. Наиболее эффективным будет режим, при котором режущий элемент совершает продольные колебания на резонансной частоте. Под воздействием кавитации клеточной структуры прилегающих к лезвию слоев ткани сухое трение переходит в полусухое или даже жидкостное. Это приводит к существенному уменьшению как нормального, так и тангенциального усилия резания, но максимальная амплитуда колебаний и частота резонанса изменяются. Поэтому указанная в инструкциях к ультразвуковым скальпелям основная частота колебаний без учета нагрузки на режущий элемент вряд ли будет резонансной. С другой стороны, в цепочке упругих элементов содержится концентратор колебаний, позволяющий увеличить амплитуду продольных колебаний рассекающего элемента, форма и размеры которого влияют на амплитудно-частотные характеристики скальпеля. Еще одним важным элементом является пьезокерамический преобразователь, который может быть многосекционным, а может иметь и неоднородную предварительную поляризацию [5–7].

Для моделирования работы ультразвукового режущего прибора была рассмотрена конечноэлементная модель составной системы пьезокерамических и упругих элементов, один из которых имеет превалирующий над остальными продольный размер, с целью изучения влияния параметров физического и геометрического характера на его продольные колебания. Такая система близка к конструкции медицинского ультразвукового скальпеля и может быть использована при моделировании его работы.

Среди факторов, которые влияют на собственные частоты исследуемых колебаний, можно выделить три основные группы: геометрические параметры, материальные свойства, неоднородная поляризация пьезоэлемента. Кроме этого, при расчете рабочих характеристик учитывалась среда, с которой контактирует рассекающий элемент. С этой целью была использована модель вязкой акустической жидкости. Для анализа поведения скальпеля в различных типах тканей параметрами этой жидкости (например, вязкостью и плотностью) можно варьировать. Различные подходы к моделированию свойств живых тканей, в том числе и акустических жидкостей, представлены в [8, 9].

В данной работе построена параметризованная геометрия модели, проведена серия численных экспериментов и определены изменения собственных частот в зависимости от размеров отдельных элементов системы. Кроме того, были проанализированы амплитудно-частотные характеристики системы на частотах, близких к резонансу в зависимости от физических свойств акустической среды жидкости.

Материалы и методы. Для исследования была взята система, состоящая из цепочки упругих и пьезокерамических элементов, показанных на рис. 1.

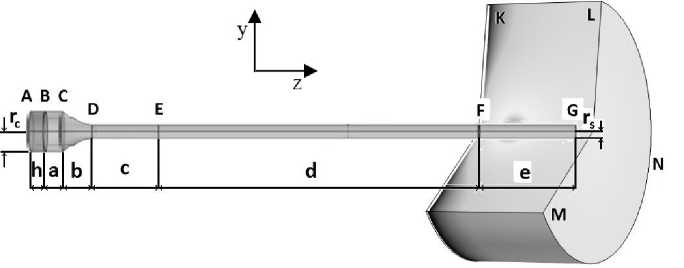
Рис. 1. Параметризованная геометрия модели скальпеля в осесимметричной и в трехмерной постановке в пакете COMSOL

Fig. 1. Parametrized scalpel model geometry in axisymmetric and three-dimensional setting in COMSOL package

Здесь участки AB, BD, DG — пьезокерамический элемент, концентратор колебаний и стержневой элемент соответственно. Все элементы имеют осесимметричное строение. Пьезоэлемент представляет собой цилиндрический пьезокерамический преобразователь с толщиной h и предварительной поляризацией, направленной по толщине. Электроды нанесены на лицевые поверхности пьезокерамического цилиндра, и на них подается разность потенциалов, из- меняющаяся по гармоническому закону во времени. Материал концентратора колебаний и стержневого элемента — нержавеющая сталь. Контактное взаимодействие между преобразователем и концентратором колебаний и между концентратором и стержнем считается безотрывным. Сечение А преобразователя закреплено; на боковой поверхности имеет место гладкий жесткий контакт.

Последнее условие выполнено и для концентратора напряжений на участке BC длиной a. Остальная боковая поверхность длиной b свободна от механических напряжений. Для стержня принималось условие гладкого жесткого контакта на участке DE длиной c. На участке EF длиной d принимались нулевые напряжения. На участке FG длиной e и на его концевом сечении G имеет место сопряжение с акустической средой KLNM. При этом считалось, что на лицевой поверхности, проходящей через точку K, звуковое давление равно нулю, на боковой поверхности KL имеет место условие импедансного типа, а лицевая поверхность LNM — непроницаемая плоскость.

Каждая из отмеченных выше сред описывается линейными моделями, которые для упрощения представим в векторном виде.

Пьезокерамическая среда:

• V- о = рю u ;

• V- D = 0;

о = C : £ - e ^T - E ;       £ = 1/2( V u + V u ^T );

D = e : £ + э - E ;          E = —Vф ;

в которой о,£, D, E, u, ф,С, e, э, р,ю — тензор напряжений, тензор деформаций, вектор электрического смещения, век- тор электрического поля, вектор перемещения, электрический потенциал, тензор упругих постоянных, тензор пьезоэлектрических констант, тензор диэлектрических проницаемостей, плотность материала керамики и круговая частота соответственно.

Упругая среда:

V- о = р к ю u ;

о = X к tr £ I + 2 ц к £ ;

£ = 1/2( V u + V u ^T );

в которой σ,ε,u, I, λk,μk,ρk — тензор напряжений, тензор деформаций, вектор перемещения, единичный тензор, ко- эффициенты Ламе и плотность материала концентратора колебаний и стержня соответственно (k = 1,2). Затухание в этих материалах моделируется с помощью комплексных коэффициентов Ламе, и тангенс угла потерь равен 0,0001.

Акустическая среда:

V-|—- V p

V р с

—

k e ² q p

ρ _с

( а ²

Л.    7 2 I ю I

= 0; k eq = I I ; c c = c

V c c )

1 + i ю

4μ a

3  ^{+ ц} b

ρ c ²

0.5

ρ c 2

;  р с = -2-;

c_c ²

V

У

в которой p,ρ, c ,μ a ,μ b — акустическое давление, плотность жидкости, скорость звука в ней, динамическая вязкость и второй коэффициент вязкости среды соответственно.

Граничные условия и условия сопряжения были подробно описаны выше, они очевидны, поэтому математические формулы для них выписываться не будут. Добавим только, что, если будут рассматриваться неоднородно поляризованные керамические таблетки, то упругие, пьезоэлектрические и диэлектрические характеристики таких сред будут представлять функции координат области, занятой керамикой.

Для описания геометрии всех элементов системы были разработаны три конечноэлементные модели. Две осесимметричные модели были построены в пакетах ACELAN и COMSOL. Третья модель построена в пакете COMSOL для случая 3D.

В основе каждой модели лежит параметризованная геометрия, представленная на рис. 1, где также указаны независимые параметры, отвечающие за геометрию модели. В левой части системы расположен пьезокерамический цилиндр, выделенный более темным цветом. Следующий элемент — стальной концентратор колебаний, состоящий из двух геометрических компонентов: цилиндра и конусообразного переходника. В реальных конструкциях хирургических инструментов толщины преобразователя и радиусы концевых сечений концентратора связаны с длинами распространяющихся волн. В предлагаемом варианте мы отказались от дополнительных ограничений на геометрические параметры, чтобы иметь возможность получить более общие результаты. При этом в модель заложена возможность изменять функциональным образом диаметр конусообразной части. С этой целью образующая конуса в глобальных координатах в плоскости YZ описывается квадратичным уравнением:

Механика

y ( z ) = kz ² + k 1 z + к ₂ ;

rs — rc + к ( z 0 — z 2 )

^k 1                                     ;

z 2 ^— z 0

к2 = rc — к1 z 2;     z 0 = hc + a;     z1 = z 0 + b, которое позволяет проводить численные эксперименты для вогнутых и выпуклых профилей направляющей, изменяя лишь один параметр k, как это показано на рис. 2.

Рис. 2. Различные формы переходника между пьезоэлементом и стержнем (форма определяется параметром k )

Fig. 2. Various forms of the adapter between the piezoelectric cell and the rod (the shape is determined by the parameter k)

Следующий в цепочке упругих элементов — стержень, имитирующий тело рассекателя. Стержень разделен на три условные части, на каждой из которых задаются свои граничные условия, как говорилось выше. Акустическая часть также представлена на рис. 1 затемненным цветом и располагается справа. Для удобства в этой среде был сделан разрез, позволяющий оценить ее влияние на продольные колебания стержневой конструкции. Полный список независимых геометрических параметров приводится в табл. 1.

Таблица 1

Изменяемые параметры модели Model changing parameters

Table 1

Обозначение Начальное значение Описание rc 7,5 мм Радиус керамического диска h 5 мм Толщина керамического диска a 5 мм Толщина слоя металла b 10 мм Толщина переходника rs 2,5 мм Радиус стержня k –80 Безразмерный параметр кривизны образующей конуса переходника c 0,02 Длина начального сегмента стержня d 0,2 Длина среднего сегмента стержня e 0,03 Длина сегмента стержня, погруженного в жидкость μ Pa∙s Вязкость жидкости ρ 1500 кг/м3 Плотность жидкости cs 1900 м/с Скорость звука в жидкости

Физические параметры жидкости, симулирующей поведение среды, с которой происходит контактное взаимодействие, находятся в нижней части этой таблицы. Это скорость распространения звука, плотность и динамическая вязкость (второй коэффициент вязкости принимался равным нулю). Более подробно математические модели электро-упругих и упругих тел (1)–(2), нагруженных на акустическую среду (3), используемые в пакете ACELAN, представлены в [10].

Результаты исследования. Для осесимметричной и трехмерной моделей была проведена оценка качества конечноэлементных сеток. Задача на собственные значения решалась на сетках с различными размерами. Измельчение сетки продолжалось до тех пор, пока дальнейшее уменьшение размеров не начинало влиять на результат по заданной погрешности. В нашем случае результатом исследования была выбрана первая собственная частота резонанса продольных колебаний f 1 . Продольные колебания отбирались посредством перебора собственных форм колебаний. В табл. 2 приведены результаты расчетов, по итогам которых определены оптимальные размеры сеток, позволяющие получить достоверные результаты с минимальным числом элементов.

Таблица 2

Table 2

Результаты подбора сеток

Grid selection results

	2D		3D
Размер элемента [min; max] (м)	f 1 (Гц)	Степеней свободы	f 1 (Гц)	Степеней свободы
[6,8 ∙10–4; 0,034]	4900,8	827	5050	3300
[1,02∙10–4; 0,0228]	4900,3	1059	5011,4	6316
[1,02∙10–4; 0,018]	4900,1	1095	4934,7	22960
[4,25∙10–5; 0,0126]	4900,1	1559	4932,1	178816

Представленные результаты позволяют сделать вывод, что для достижения заданной точности осесимметричная модель позволяет использовать значительно меньшее число степеней свободы. Так, с погрешностью 5 = 0 , 6% в осесимметричной модели можно взять в 115 раз меньше конечных элементов, что важно при решении задач оптимизации по параметрам. Однако в дальнейшем возникнет необходимость использовать трехмерную модель, когда будет учитываться неосесимметричный вид наконечника стержня и неосесимметричная форма внешних воздействий.

Первый этап численного эксперимента заключался в валидации моделей путем сравнения различных реализаций при решении задачи на собственные значения. Была отработана методика определения первых трех рабочих частот устройства, которые соответствуют продольным колебаниям стержня (в табл. 2 указано значение только первой из них).

Следующий шаг численных экспериментов заключался в сравнении результатов расчета собственных частот продольных колебаний, полученных разными моделями и разными конечноэлементными комплексами.

В частности, в пакете ACELAN была построена осесимметричная модель этой системы. В табл. 3 представлены результаты вычисления первых двух собственных частот.

Таблица 3

Table 3 Результаты решения задачи на собственные значения на оптимальных сетках в различных пакетах

Results of solving eigenvalue problem on optimal grids in various packages

Модель	f 1 (Гц)	f 2 (Гц)
ACELAN	4907	14711
COMSOL (2D)	4900,1	14691
COMSOL (3D)	4932,1	14782

Сравнение результатов показывает, что осесимметричные модели согласуются с очень высокой точностью. Разница между трехмерной моделью и осесимметричной может быть вызвана сложностью построения объемной сетки на наиболее тонких участках геометрии.

Возможности постпроцессора пакета COMSOL позволяют построить трехмерное изображение по итогам решения осесимметричной задачи. Здесь и далее в работе приводятся результаты постпроцессорной обработки решений осесимметричной задачи.

Механика

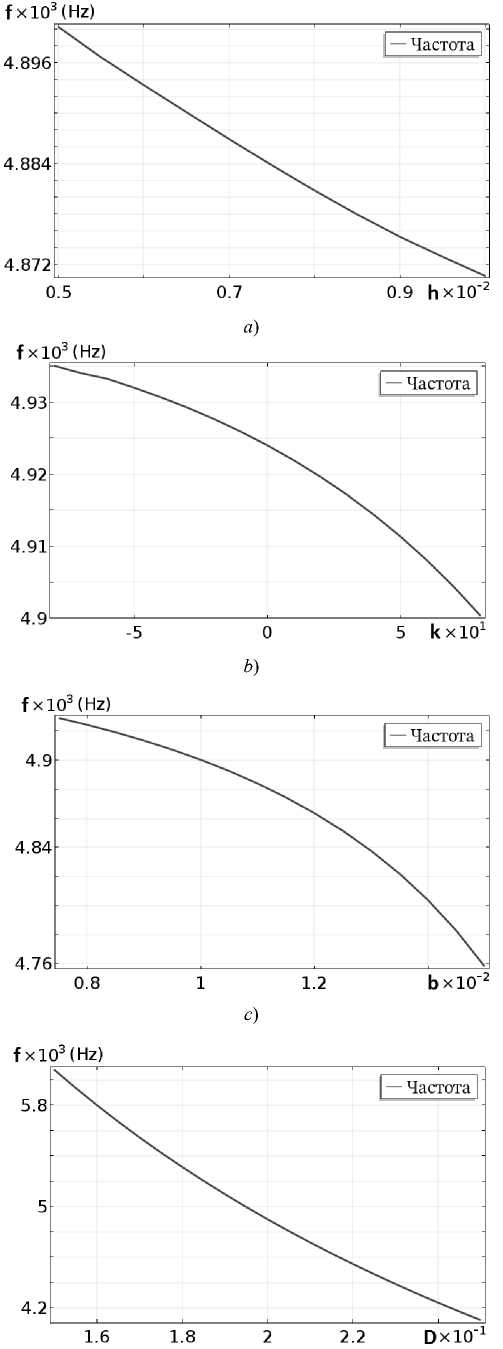
Была проведена оценка влияния геометрических параметров на собственные частоты (СЧ). На рис. 3 представлены зависимости СЧ от различных геометрических параметров.

d )

Рис. 3. Влияние на собственную частоту геометрических параметров: толщины h пьезопреобразователя (a); параметра кривизны k направляющей концентратора колебаний (b); толщины b концентратора колебаний (c); длины D стержня (d)

Fig. 3. Effect on eigenfrequency of geometric parameters: thickness h of piezoelectric transformer (a); curvature parameter k of oscillation concentrator guide (b); thickness b of oscillation concentrator (c); rod length D (d)

Из рисунков видно, что с увеличением толщины преобразователя, равно как и с увеличением длины стержневой части, первая собственная частота уменьшается. Это уменьшение будет значительным, когда приходится увеличивать длину стержневой части, но практически отсутствует при малом изменении толщины преобразователя. Характерно, что на собственную частоту также практически не влияет кривизна концентратора напряжений и его длина.

Другой важной характеристикой является амплитудно-частотная характеристика (АЧХ) продольных колебаний вблизи резонансных частот. Так, на рис. 4 приведены результаты расчета АЧХ продольных колебаний вблизи резонансной частоты при определенных значениях независимых физических и геометрических параметров.

|Uz|×10-4

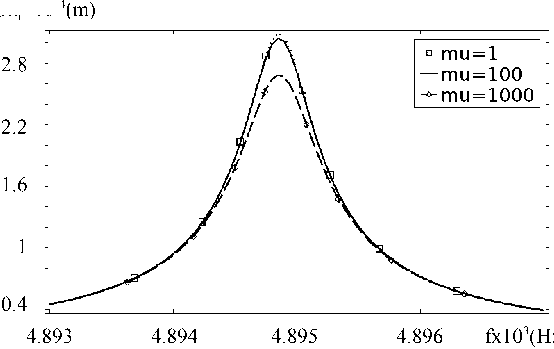
Рис. 4. АЧХ вынужденных колебаний скальпеля при различных значениях вязкости

Fig. 4. FRF of forced scalpel oscillations at various values of viscosity

Расчеты проводились с учетом акустической жидкости, в которую вставлен конец стержневой части. Воздействие акустической жидкости приводит к демпфированию, при котором частота резонанса меняется в зависимости от свойств среды. На рис. 4 изображены АЧХ продольных колебаний для различных значений динамической вязкости. Второй коэффициент вязкости принимался равным нулю.

Интересно отметить, что при изменениях вязкости акустической среды в большом диапазоне АЧХ изменяется незначительно. Отсюда можно сделать вывод, что основным фактором, влияющим на амплитуду колебаний в окрестности первого резонанса продольных колебаний, является затухание в упругой среде. Таким образом, увеличение вязкости акустической среды более чем на порядок не приводит к значительному снижению амплитуды колебаний стержневого звена. Интересно также отметить, что вязкость оказывает влияние на амплитуду колебаний, но не на частоту. Это может быть связано с небольшой площадью сечения скальпеля.

Обсуждение и заключения.   В настоящей работе были исследованы резонансные частоты продольных колебаний системы, состоящей из цепочки разных по физическим параметрам элементов: пьезокерамического, двух упругих и акустического. С этой целью были построены осесимметричные и трехмерные конечноэлементные модели. Для сравнения были выбраны два конечноэлементных пакета COMSOL и ACELAN. Обнаружено хорошее совпадение результатов по собственным частотам для осесимметричной задачи. Построенная трехмерная модель послужит в дальнейшем при моделировании несимметричных задач. Проведены оценки влияния геометрических параметров на значение первой собственной частоты. В частности, рассмотрены варианты, в которых варьировались следующие параметры: толщина пьезопреобразователя; кривизна и толщина концентратора колебаний; длина стержневого звена. Другим важным параметром исследования явилась АЧХ продольных колебаний вблизи первой резонансной частоты. Отмечено, что малое изменение динамической вязкости акустической среды мало влияет на эту характеристику. А заметное увеличение этой вязкости приводит лишь к снижению амплитуды колебаний, но практически не изменяет частоту резонанса. Полученные результаты могут представлять интерес при конструировании ультразвуковых режущих медицинских приборов.