Влияние геометрических параметров обделки на напряженно-деформированное состояние заглубленного тоннеля

Постановка и аналитическое решение задачи

В тех случаях, когда обделка кругового тоннеля глубокого заложения является тонкостенной конструкцией, в качестве расчетной модели можно принять расположенную в упругом пространстве тонкостенную оболочку с радиусом кривизны срединного слоя R (рис.1). В силу малости толщины h 0 оболочки будем полагать, что окружающий массив контактирует с оболочкой вдоль ее срединной поверхности. Контакт между оболочкой и окружающим ее массивом будем полагать либо жестким, либо скользящим.

Пусть на внутреннюю поверхность оболочки действует нагрузка P, движущаяся с постоянной дозвуковой скоростью c в направлении оси z. Так как рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому для решения задачи можно ввести подвижную цилиндрическую систему координат (r, Ө, ŋ = z –ct), связанную с нагрузкой.

Для описания движения оболочки воспользуемся классическими уравнениями теории тонких оболочек, которые в подвижной системе координат имеют вид [ 1 ] :

• 1    _ ( 1 ^{- v} 0 ) Р 0 c 2 1 ^{д 2} u 0 п + ^{1 - v} о ^{д 2} u 0 п + ^{1 + v} о ^{д 2} u 0 е + ^v о ^д u о r _ 1 ^{- v} о ( _р )

_         2 ц ₀      ] дп ²     2 R ² де ²      2 R дпде R дп 2 Ц ₀ h ₀ ^(п    q ^п )

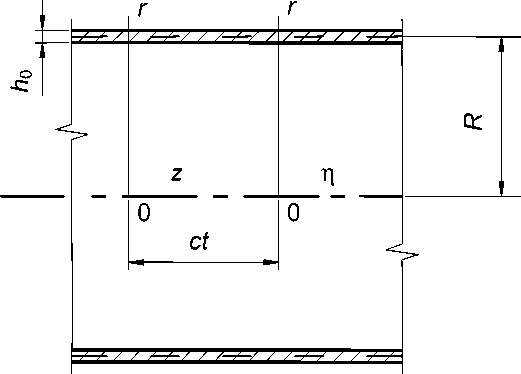
Рис. 1. Тонкостенная оболочка в упругом пространстве

^{1 + v} о ^д u 0 п ₊ ^{( 1 - v} о ) ( 1 _ ^р о c ^{2 1 д 2} u о е ₊ ^{1 д 2 u} о е + ^{1 д u} о r _ ^{1 - v} о ( р

2 R дпде 2 V Ц ₀ J дп ² R ² де ² R ² де 2 Ц ₀ h ₀ ^е

^- q е ) ,

^{( P}r ^- Q r ) ,

^V о ^д u 0 п , 1 ^д u 0 е , ^h о V7 2V7 2..     1 ⁽1 ^{- v} о ^{) р} о c ^д u о r , u о r _    ^{1 - v} о

+              +      * * u ++       =

R дп R ² де 12         ^{0 r} 2 ц ₀ дп ² R ²      2 ц ₀ h ₀

где u0ŋ, u0Ө, u0r – перемещения точек срединной поверхности оболочки; Pŋ(Ө, ŋ), PӨ(Ө, ŋ), Pr(Ө, ŋ) – составляющие интенсивности подвижной нагрузки P(Ө, ŋ);                                             – состав- q п _ ° rп |r_ R ’ q е _ ° rе lr_ R , q r _ ° rr lr_ R ляющие реакции окружающей оболочку среды; crj — компоненты тензора напряжений в среде (j = r, е, п); v0, Цо, р0; - соответственно коэффициент Пуассона, модуль сдвига и плотность материала оболочки; V2 - оператор Лапласа.

Для описания движения массива используем динамические уравнения теории упругости в подвижной системе координат

м ¹2

V p

M r 1

⁵ 7

grad

,.               1         2 д u .

div u + --- -V u = ----

M 5 дп ²

Здесь u – ве ктор смещения упругой среды; M p = c/c p , M s = c/c s – числа Маха; c _{p =} ( λ + 2 µ)/ρ , c_s = Vµ/ρ – скорости распространения волн расширения – сжатия и сдвига в среде; λ = 2 µν /(1-2 ν );

ν , µ , ρ – соответственно коэффициент Пуассона, модуль сдвига и плотность среды.

В случае жесткого сцепления оболочки с окружающей средой ujIr=R = u0j, j = η, θ, r.                                                                                         (3)

При скользящем контакте и двухсторонней связи оболочки со средой

σ rj I = 0, j= η,θ, rj r = R ur I r=R      u0r

Здесь ur, u_Ө, u_ŋ – компоненты вектора u . Заметим, что при скользящем контакте в уравнениях (1) q_η = q Ө = 0.

Задача сводится к совместному интегрированию уравнений движения оболочки (1) и массива (2) при выполнении граничных условий (3) или (4).

Выражая u через потенциалы Ламе u = grad ϕ 1 + rot (ϕ 2 e η ) + rot rot (ϕ 3 e η ) ,                                (5)

преобразуем уравнение (2) к виду

∇ ² ϕ j = M ² j ^{∂ ϕ j} , j = 1, 2,3 ,                                     (6)

∂η ²

где M 1 = M p , M 2 = M 3 = M s .

Рассмотрим вначале подвижную нагрузку с произвольной зависимостью от угловой координаты и изменяющуюся вдоль η синусоидально

∞

P (θ,η )= p (θ)eiξη , p (θ)= ∑ Pne n = -∞

P j ( θ , η ) = p j ( θ ) e ^{i ξη} , p j ( θ ) = ∑ P nj e ^{in θ} , j = r , θ , η . n = -∞

Потенциалы φ j также будем искать в виде периодических функций по ŋ φ j (r, Ө, η) = Ф j (r, Ө)e^{i ξη} .

Из (6) и (8) следует, что

∆ 2 Φ j - m ² j ξ ² Φ j = 0 , j = 1 , 2 , 3 .                                                                                        (9)

Здесь m² j = 1 - M² j , m 1 ≡ m p , m 2 = m 3 ≡ m s , ∆ 2 – двумерный оператор Лапласа.

Выразив компоненты напряженно-деформированного состояния среды через потенциалы Ламе, можно получить выражения для перемещений u l* и напряжений σ *lm (l, m = r , θ , η ) от синусои- дальной нагрузки как функции от Фj.

Так как скорость нагрузки меньше скорости распространения волн сдвига в среде, то М s < 1 (m s 0) и решения (9) можно представить в виде

∞

Φ j = ∑ anj K n (kjr)einθ , n = -∞ где Kn(kjr) – функции Макдональда, k j = I m jξ I ; anj – неизвестные коэффициенты, подлежащие определению.

**

Подставляя (10) в выражения для u l и σ lm , получим новые выражения, где неизвестными будут только коэффициенты a _nj . Для определения последних в зависимости от условия сопряжения оболоч- ** ки со средой воспользуемся граничными условиями (3) или (4), переписанными для u l и σ lm .

Для перемещений точек срединной поверхности оболочки при действии синусоидальной нагрузки, имеем ∞

u 0 ^* j ( θ , η ) = U 0 j ( θ ) e^{i ξ η} , U 0 j ( θ ) = ∑ u 0 nj e^{in θ} , j = r , θ , η . n = -∞

Подставляя (7) и (11) в уравнения (1), для n -го члена разложения получим ε 12 u 0 n η ⁺ ν 02 n ξ 0 u 0 n θ ^- 2 i ν 0 ξ 0 u 0 nr ⁼ G 0 ( P n η ^- q n η ) , ν 02 n ξ 0 u 0 n η ⁺ ε 2 u 0 n θ ^- 2 inu 0 nr ⁼ G 0 ( P n θ ^- q n θ ) , 2 i ν ₀ ξ ₀ u _{0 n η} + 2 inu _{0 n θ} + ε ₃ ² u _{0 nr} = G ₀ ( P _nr - q _nr ) , 2      2     2      2      2     2      2     2     2      2          22

^где ε ₁ = α ₀ - ε ₀ , ε ₂ = β ₀ - ε ₀ ,    ε ₃ = γ ₀ - ε ₀ ,    ε ₀ = ν ₀₁ ξ ₀ M _s0 ,    ξ ₀ = ξ R ,

α 0² = 2 ξ 0² + ν 01 n ² , ξ 0 = ξ R ,

ν ₀₁ = 1 -ν ₀ , ν ₀₂ = 1 +ν ₀ , M_{s 0}

β 02 = ν 01 ξ 02 + 2 n 2 , γ 02 = χ 2 (ξ 02 + n 2 )2

=c, c =     0    2      001

= cs0 =      , χ =      , G0 = - cs0 ρ0         6R2 µ0h0

при r = R: qnη =(σ*rη)n , qnθ = (σ*rθ)n , qnr = (σ*rr)n – в случае жесткого контакта; qnη =0 , qnθ = 0 , qnr = (σrr )n – в случае скользящего контакта.

Разрешая (12) относительно u0nη , u0nθ , u0nr , находим u 0 nη = G 0 ∑= δη (Pnj - q nj ),

u 0 n θ = G 0 ∑ δδ θ j (P nj - q nj ), j=1 δ n u 0 nr = G 0 ∑= δδ rj (Pnj - q nj ).

Здесь δ n = ( ε 1 ε 2 ε 3 )² - ( ε 1 ξ 1 )² - ( ε 2 ξ 2 )² + 2 ξ 1 ξ 2 ξ 3 , δ η 1 = ( ε 2 ε 3 ) ² - ξ 1² , δ η 2 = ξ 1 ξ 2 - ξ 3 ε 3² , δ η 3 = i ( ε ²2 ξ 2 - ξ 1 ξ 3 ), δ_{θ 1} = δ_{η 2}, δ_{θ 2} = ( ε ₁ ε ₃)² - ξ ²₂, δ_{θ 3} = i ( ε ₁ ² ξ ₁ - ξ ₂ ξ ₃), δ r 1 = -δ η 3 , δ r 2 = -δ θ 3 , δ r 3 = ( ε 1 ε 2 )² - ξ 3 ², ξ 1 = 2 n , ξ 2 = 2 ν 0 ξ 0 , ξ 3 = ν 02 ξ 0 n ;

для P nj и q nj индекс j = 1 соответствует индексу ŋ, j = 2 –Ө, j = 3 – r .

Подставляя (13), в зависимости от типа контакта, в (3) или (4) и приравнивая коэффициенты рядов Фурье-Бесселя при einӨ, получим бесконечную систему линейных алгебраических уравнений блочно-диагонального вида для определения коэффициентов anj, решение которой находим извест-

∆ _n ( ξ , c )

ным методом, если соответствующий для каждого n определитель системы отличен от нуля.

Зная решение задачи для синусоидальной нагрузки, реакцию упругого пространства на движущуюся апериодическую нагрузку характерного для транспортируемых объектов типа P(Өŋ) = p(Ө)p(ŋ) формально получаем при помощи суперпозиции, используя представление нагрузки и компонент НДС среды в виде интегралов Фурье: ∞    ∞∞

P ( θ , η ) =         P ^* ( θ , ξ ) e^{i ξη} d ξ = p ( θ ) p ( η ) = p ( θ )         p ^* ( ξ ) e^{i ξη} d ξ , p ^* ( ξ ) =     p ( η ) e ^{-i ξη} d ξ ;

2 π                                     2 π

-∞                                        -∞                       -∞

∆ _n ( ξ , c ) ≠ 0

Поэтому, если 0 <  c <  c _(0)* , то

^A n ⁽± ^ ( n ) l , c ( n ) ) = 0, 5A n ⁽± ^ ( n ) 1 , c ( n ) )/d^ 0, I = 1,2 .

В этих случаях решение существует, если ранг расширенной матрицы равен рангу матрицы системы уравнений для данной n -моды. Как показано в [ 2 ] , при движении с такими сверхкритическими скоростями нагрузка генерирует позади себя свободные цилиндрические незатухающие вдоль оси оболочки гармонические волны частоты W ( n ) l = c ^ ( n ) l и длины X ( _n ) l = 2 n / ^ ( _n ) l , движущиеся вдоль поверхности оболочки вслед за действующей нагрузкой с той же скоростью. Амплитуда этих волн не зависит от z и экспоненциально затухает при r ^ ^ .

При c=c (n)* точки ξ (n)1 и ξ (n)2 сливаются в одну ξ (n)* . Стационарного решения задачи в этом случае не существует. Для таких скоростей в оболочке возникают резонансные явления, для изучения которых следует переходить к нестационарной постановке задачи. Значение параметра задачи c = c (n)* можно характеризовать как точку бифуркации решения, при переходе через которую возникает неустойчивость движения. Этот факт может оказаться существенным для практики строительства подземных транспортных сооружений.

Анализ результатов расчета

В качестве примера рассмотрим тоннель глубокого заложения в породах различной жесткости:

• -    в известняке (ν = 0,25, µ = 2,8·10³ МПа, p = 2,65·10³ кг/м³; c _s = 1028м/с);

• -    в алевролите (ν = 0,28, µ = 4,69·10³ МПа, p = 2,7·10³ кг/м³; c _s = 1318м/с);

• -    в песчанике (ν = 0,28, µ = 7,8·10³ МПа, p = 2,5·10³ кг/м³; c _s = 1766м/с).

Исследуем влияние толщины h 0 стальной (ν= 0,3, µ 0 = 8,08·10³ МПа, p = 7,8·10³ кг/м³) тонкостенной обделки тоннеля и радиуса тоннеля R на его напряженно-деформированное состояние.

В таблицах 1–6 для различных значений h ₀ и R представлены результаты расчетов напряженно-деформированного состояния контура поперечного сечения ŋ = 0 тоннеля в проходке при воздействии движущейся с докритической скоростью c = 200 м/с нормальной осесимметричной нагрузки интенсивностью P⁰, равномерно распределенной по внутренней поверхности тоннеля в интервале |η| ≤ 0,2 м.

Таблица 1

Радиальные перемещения u _r = u r р / P контура поперечного сечения тоннеля при h 0 = 0,01м

Породный массив	Тип контакта	R , м
	оболочки с мас-	1,0	1,5	2,0	3,0	4,0	6,0	8,0
	сивом	u r , м
известняк	жесткий	0,169	0,212	0,242	0,283	0,317	0,361	0,382
	скользящий	0,175	0,220	0,252	0,295	0,331	0,376	0,399
алевролит	жесткий	0,177	0,217	0,245	0,283	0,315	0,356	0,376
	скользящий	0,182	0,223	0,252	0,291	0,324	0,366	0,386
песчаник	жесткий	0,185	0,223	0,250	0,286	0,318	0,358	0,376
	скользящий	0,189	0,228	0,255	0,292	0,324	0,365	0,385

Таблица 2

Радиальные перемещения u r = u r ц / P контура поперечного сечения тоннеля при h ₀ = 0,02м

Породный массив	Тип контакта оболочки с массивом	R , м
		1,0	1,5	2,0	3,0	4,0	6,0	8,0
		u r , м
известняк	жесткий	0,146	0,192	0,225	0,270	0,304	0,350	0,373
	скользящий	0,152	0,201	0,236	0,284	0,321	0,369	0,393
алевролит	жесткий	0,161	0,203	0,233	0,274	0,306	0,348	0,370
	скользящий	0,166	0,210	0,241	0,284	0,318	0,361	0,383
песчаник	жесткий	0,173	0,213	0,241	0,280	0,311	0,352	0,373
	скользящий	0,178	0,219	0,248	0,288	0,321	0,362	0,383

Осевые нормальные напряжения о _пт| = о_пп / P на контуре поперечного сечения тоннеля при h 0 = 0,01м

Породный массив	Тип контакта оболочки с массивом	R , м
		1,0	1,5	2,0	3,0	4,0	6,0	8,0
		о пп
известняк	жесткий	-0,413	-0,459	-0,491	-0,490	-0,565	-0,608	-0,568
	скользящий	-0,677	-0,779	-0,854	-0,832	-1,026	-1,132	-1,029
алевролит	жесткий	-0,502	-0,550	-0,588	-0,580	-0,670	-0,721	-0,672
	скользящий	-0,713	-0,796	-0,868	-0,830	-1,021	-1,122	-1,019
песчаник	жесткий	-0,561	-0,607	-0,649	-0,638	-0,735	-0,791	-0,736
	скользящий	-0,732	-0,800	-0,872	-0,825	-1,014	-1,114	-1,011

Таблица 4

Осевые нормальные напряжения о _пп = о_пп / P на контуре поперечного сечения тоннеля при h ₀ = 0,02 м

Породный массив	Тип контакта оболочки с массивом	R , м
		1,0	1,5	2,0	3,0	4,0	6,0	8,0
		о пп
известняк	жесткий	-0,337	-0,387	-0,415	-0,432	-0,487	-0,522	-0,488
	скользящий	-0,623	-0,752	-0,826	-0,871	-1,019	-1,116	-1,021
алевролит	жесткий	-0,422	-0,474	-0,503	-0,515	-0,585	-0,629	-0,586
	скользящий	-0,670	-0,777	-0,840	-0,858	-1,017	-1,113	-1,014
песчаник	жесткий	-0,479	-0,528	-0,559	-0,564	-0,644	-0,691	-0,644
	скользящий	-0,698	-0,789	-0,847	-0,844	-1,013	-1,108	-1,008

Таблица 5

Породный массив	Тип контакта оболочки с массивом	R , м
		1,0	1,5	2,0	3,0	4,0	6,0	8,0
		о ее
известняк	жесткий	0,096	0,003	-0,066	-0,117	-0,215	-0,293	-0,285
	скользящий	0,048	-0,061	-0,142	-0,191	-0,321	-0,417	-0,395
алевролит	жесткий	0,052	-0,053	-0,131	-0,180	-0,292	-0,377	-0,362
	скользящий	0,007	-0,110	-0,199	-0,242	-0,383	-0,484	-0,455
песчаник	жесткий	0,046	-0,063	-0,145	-0,193	-0,309	-0,396	-0,379
	скользящий	0,009	-0,108	-0,200	-0,240	-0,382	-0,482	-0,454

Таблица 6

Породный массив	Тип контакта оболочки с массивом	R , м
		1,0	1,5	2,0	3,0	4,0	6,0	8,0
		о ее
известняк	жесткий	0,079	-0,002	-0,059	-0,122	-0,201	-0,272	-0,266
	скользящий	0,026	-0,075	-0,145	-0,218	-0,323	-0,411	-0,392
алевролит	жесткий	0,049	-0,048	-0,114	-0,176	-0,272	-0,351	-0,339
	скользящий	-0,005	-0,119	-0,195	-0,263	-0,385	-0,480	-0,454
песчаник	жесткий	0,051	-0,053	-0,124	-0,183	-0,286	-0,369	-0,355
	скользящий	0,004	-0,114	-0,194	-0,254	-0,383	-0,480	-0,453

Тангенциальные нормальные напряжения о ев = оее/P на контуре поперечного сечения тоннеля при h0 = 0,01 м

Тангенциальные нормальные напряжения о ее = оее/P на контуре поперечного сечения тоннеля при h0 = 0,02 м

Из анализа данных табл. 1, 2 следует, что при любой толщине обделки h0 увеличение радиуса R ведет к возрастанию радиальных перемещений контура поперечного сечения тоннеля ur (прогибов тоннеля) во всех рассматриваемых породах независимо от ее контактных условий с массивом. С уменьшением h0 эта тенденция усиливается. При жестком контакте обделки с любым породным массивом ur меньше, чем при скользящем. С увеличением жесткости массива прогибы тоннеля умень- шаются. Это хорошо видно из построенных на рис. 2 по данным табл. 1 кривых изменений радиальных перемещений контура поперечного сечения тоннеля ur. = urµa/P0, м, (здесь µa – модуль сдвига алевролита) в зависимости от изменения его радиуса R, м. Кривые 1, 2, 3 построены соответственно для тоннелей проходящих в известняке, алевролите и песчанике при h0 = 0,01 м и жестком сцеплении обделки с массивом.

Анализируя напряженное состояние рассматриваемого контура сечения тоннеля, заключаем, что характерные особенности изменений нормальных напряжений |G_nn| и |о _е е | с увеличением R аналогичны особенностям изменения u r . Следует отметить следующие исключения: напряжения |о_пп| (главным образом при h 0 = 0,01м) в интервале 2 м <  R < 4 м и напряжения |G_nn| , |О вв | в интервале 6 м <  R < 8 м с увеличением R уменьшаются; в интервале 1 м <  R <  1,5 м о ₆₆ убывают, преимущественно меняя знак; увеличение толщины обделки h 0 при ее скользящем контакте с массивом приводит к возрастанию |о_пп| в интервале 2 м < R < 4 м и |О ее | практически для любого значения R ; при скользящем контакте и R >  3 м напряжения |о_пп| уменьшаются с увеличением жесткости массива, в некоторых случаях это происходит и с напряжениями |О ее | -

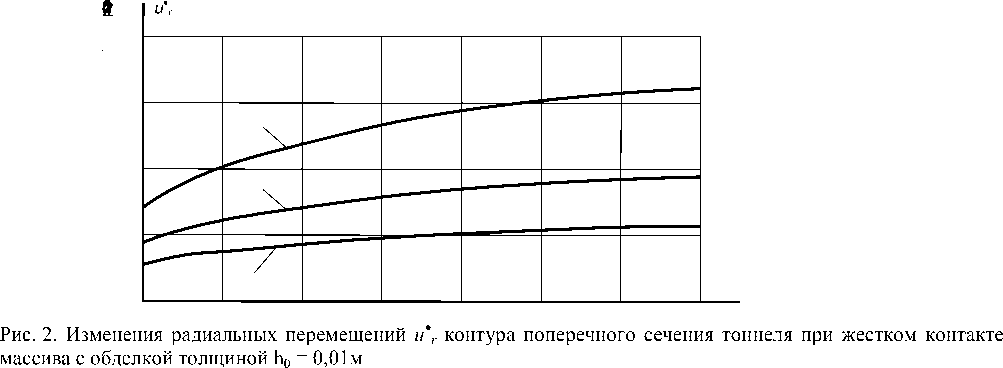
Рис. 3. Изменение перемещений u _r , м в массиве алевролита по поверхности выработки радиусом R = 2 м

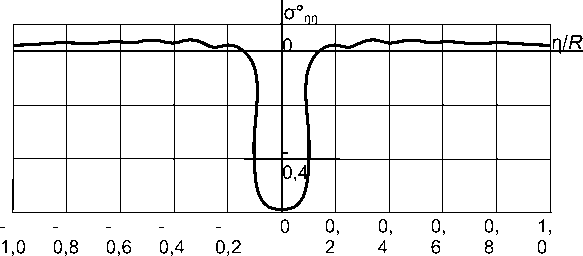
Рис. 4. Изменение напряжений g _пп в массиве алевролита по поверхности выработки радиусом R = 2 м

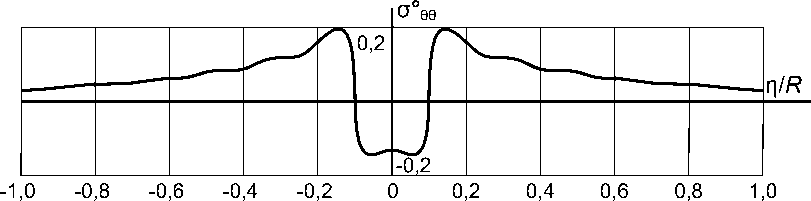
Рис. 5. Изменение напряжений о ев в массиве алевролита по поверхности выработки радиусом R = 2 м

На рис. 3-5 показаны кривые изменений компонент напряженно-деформированного состояния массива алевролита вдоль поверхности тоннеля ( r / R = 1,0) радиусом R = 2 м, жестко сопряженного с обделкой толщиной h 0 = 0,01 м. Из рисунков следует, что динамическое воздействие нагрузки на поверхность выработки практически ощутимо лишь в окрестности участка нагружения тоннеля. С удалением от места нагружения (с возрастанием | П 1 ) перемещения u r и напряжения |о_пп| , |о _ее | быстро затухают.