Влияние изменения числа двухсторонних и односторонних связей на критическую нагрузку

Пусть все связи консервативной упругой системы с n степенями свободы являются двухсторонними, а нагрузка P – однопараметрической. Собственные значения X 1 <^ 2 < k n и собственные векторы е i = [ u i 1 u i ₂ к u in ], i = 1,2, „. , n , известны. Чтобы данная конструкция могла воспринять воздействие P k , к >  2, отвечающее характеристическому числу X _k , к ней надо добавить к - 1 двухсторонних связей. Но если дополнительно накладываемые связи являются односторонними, то их потребуется на единицу больше, то есть k . Этот результат был получен в работе [5] при помощи аппарата многомерной геометрии и линейной алгебры [2], [4]. О физической реализации дополнительно накладываемых связей речь не шла, конкретные примеры не рассматривались . Однако техника расстановки добавляемых связей и техника их математического описания также не лишены интереса, тем более что при обращении к физической стороне дела обнаруживаются обстоятельства, которые полезно иметь в виду при решении задачи устойчивости систем с односторонними связями. Последующий материал излагается с использованием примеров.

На рис. 1 изображена конструкция, для которой n = 4. Через r обозначена жесткость пружины, равная реактивному моменту, который возникает при относительном повороте соединяемых элементов на единицу. На этом же рисунке приведены все 4 формы потери устойчивости, характеризуемые векторами:

е1 = [1 1,618034 1,618034 1], е2 = [1 0,618034 -0,618034 -1], е3 = [1 -0,618034 -0,618034 1], е4 = [1 -1,618034 1,618034 -1].

Ставится задача о постановке дополнительных связей, обеспечивающей возрастание критической силы до величины P 3 = X 3 r / 1 . Это означает, что добавляемые связи должны препятствовать любым перемещениям в плоскости, натянутой на собственные векторы e₁ и e₂ , обеспечивая при этом возможность перемещений, диктуемых вектором e₃ , то есть перемещений, связанных равенствами

0,618 ^ 1 + u 2 = 0, 0,618 u ₁ + u 3 = 0, u 1 - u 4 = 0.

Отсюда следует:

0,618 u 1 + u 2 = 0, 0,618 u 4 + u 3 = 0.

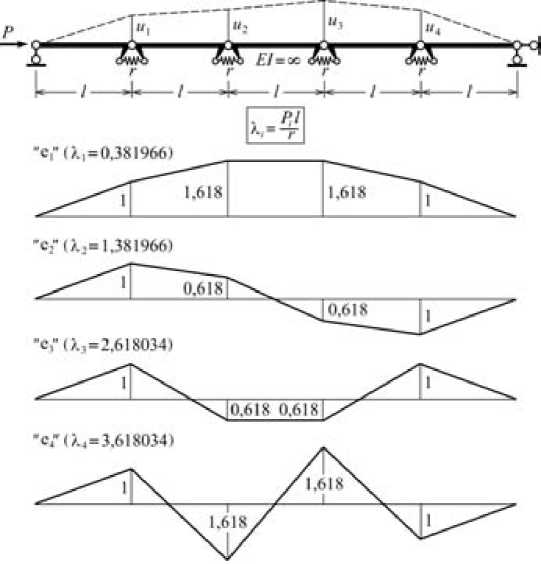
Рис. 1. Рассматриваемая конструкция и ее собственные векторы

P – сила, l – длина стержня, EI – изгибная жесткость, r – жесткость пружины, u i – перемещение узла, λ i – собственное значение, e i – собственный вектор

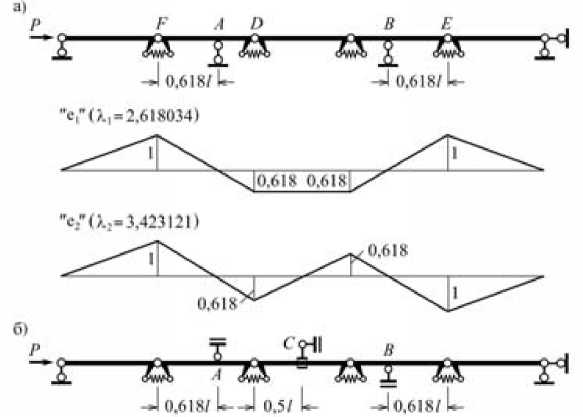
Рис. 2. Расстановка двухсторонних и односторонних дополнительных связей P – сила, l – длина стержня, λ i – собственное значение, e i – собственный вектор

Связи (2) реализуются способом, указанным на рис. 2а. На этом же рисунке приведены обе формы потери устойчивости конструкции с дополнительными связями.

Пусть теперь добавляемые связи являются односторонними. В этом случае ограничения на компоненты вектора e ₃ содержат неравенства:

0,618 м 1 + u 2 <  0, 0,618 u 1 + u 3 <  0,               (1a)

—U^ + U 4 = 0.

Расстановка связей, обеспечивающая соблюдение условий (1а), приведена на рис. 2б. Опоры A и B препятствуют перемещениям примыкающих к ним точек оси конструкции вверх и вниз соответственно, связь C не позволяет центральному звену системы поворачиваться против часовой стрелки. Допустима также и такая расстановка односторонних связей, при которой их ориентация меняется на обратную.

Векторы e₁ и e₂ остаются такими же, что и при постановке дополнительных двухсторонних связей (см. рис. 2а). Однако имеется одна особенность. Если при добавляемых двухсторонних связях собственные векторы имеют себе симметричные, то есть наряду с e₁ и e₂ существуют векторы -e₁ и -e₂ , то при подключении односторонних связей (см. рис. 2б) вектор -e₂ собственным вектором не является, ибо центральный диск конструкции по часовой стрелке поворачиваться не может.

В рассматриваемом примере запись и анализ ограничений типа (1) и (1 а ), которые накладываются на перемещения u_i , труда не составили. При решении задач большой размерности необходимо использовать специальные подходы к формированию ограничений на перемещения конструкции [1] и специальные методы решения систем неравенств и равенств, описывающих односторонние и двухсторонние связи [4]. В настоящей работе эти вопросы не обсуждаются.

Конструкция, изображенная на рис. 2б, при расчете на устойчивость рассматривается как система с двумя степенями свободы, которая имеет в своем составе двухсторонние и односторонние связи. Именно наличием односторонних связей она принципиально отличается от системы, представленной на рис. 1. Это отличие становится особенно наглядным при расстановке дополнительных связей, хотя трудности приходится преодолевать уже на стадии решения задачи на собственные значения. Если добавить к указанной выше конструкции двухстороннюю связь D (рис. 3), то задача на собственные значения получит решение

1 1 = 1,279241;

e 1 = [ — 1 0 2,441518 2,720759].

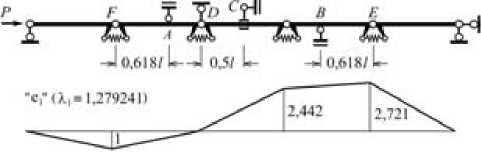
Рис. 3. Уменьшение критической нагрузки при добавлении связей

P – сила, l – длина стержня, λ _i – собственное значение, e i – собственный вектор

Точно такими же будут характеристическое число и собственный вектор, если добавленная связь D будет односторонней, препятствующей отклонению шарнира D вниз. Видно, что критическая нагрузка уменьшилась почти вдвое по сравнению с той, которую воспринимала конструкция до постановки связи D .

Если помимо связи D добавить еще связь E : двухстороннюю или одностороннюю соответствующей ориентации, то конструкция по-прежнему будет обладать подвижностью, но теперь решение задачи устойчивости изменится:

1 1 = 2,5; e 1 = [ — 1 0 0 0].

И снова характеристическое число получилось меньше значения 1 = 2,616 , отвечающего конструкции, изображенной на рис. 2а. Наконец, если две дополнительные связи разместить в точках D и F , то система сохранит две степени свободы, и задача на собственные значения будет иметь два решения:

1 1 = 1,451416 < 2,618: e 1 = [0 0 1 1,215250];

1 ₂ = 3,215260: e₂ = [0 0 1 — 0,548584].

Таким образом, добавление связей к конструкции с односторонними связями может привести как к увеличению, так и к уменьшению критической нагрузки, а также как к уменьшению, так и к увеличению степеней свободы системы. Аналогично, при устранении связей критическая нагрузка системы и число ее степеней свободы могут как уменьшаться, так и увеличиваться. Объяснить это можно следующим образом. При наложении (устранении) связей жесткость конструкции рассматриваемого типа увеличивается (уменьшается) либо остается прежней. С другой стороны, такие действия могут привести к блокировке (разблокировке) некоторых односторонних связей, что влечет за собой снижение (возрастание) жесткости системы. Каким в результате окажется баланс, зависит исключительно от конкретных условий задачи.

Эффект дестабилизирующего влияния добавляемых связей на устойчивость конструкции известен. Но если все связи конструкции двухсторонние, то такой эффект обнаруживается столь редко, что может быть продемонстрирован лишь на специально подобранных примерах. В этих примерах рассматриваются конструкции, ряд стержней которых имеют растягивающие усилия, существенно влияющие на сопротивляемость конструкции потере устойчивости. Связи к этой конструкции добавляются так, чтобы растягивающие усилия нейтрализовать. При специальном подборе схемы конструкции, ее параметров и мест расстановки связей иногда удается уменьшить критическую нагрузку. Ведь не случайно в монографии, содержащей раздел, который посвящен задачам устойчивости конструкций с двухсторонними связями, имеется следующая фраза: «Бытующий среди инженеров упрощенный взгляд о безусловном стабилизирующем влиянии связей может привести к грубым ошибкам» [3]. Ясно, что если бы обсуждаемая дестабилизация относилась к рядовым явлениям, то никакого «упрощенного взгляда» не было бы. Однако для систем с односторонними связями дело обстоит иначе, так как иной является причина дестабилизации.

• 2.    Рашевский П . К . Риманова геометрия и тензорный анализ. М.: Наука, 1985. 664 с.

• 3.    Сливкер В . И . Строительная механика. Вариационные основы. М.: Изд-во Ассоциации строительных вузов,

2005. 708 с. 4. Черников С . Н . Линейные неравенства. М.: Наука, 1968. 488 с. 5. Шулькин Ю . Б . Влияние односторонних связей на величину критической нагрузки // Исследования по механике строительных конструкций и материалов: Межвузовский тематический сборник трудов. Л.: ЛИСИ, 1985. С. 56–63.