Влияние изменения коэффициента термического расширения на термомеханическую деформацию цилиндров с ауксетичностью в плоскости на основе повторно-входящих ячеек

ВЕСТНИК ПНИПУ. МЕХАНИКА № 6, 2024PNRPU MECHANICS BULLETIN

Механические метаматериалы – это искусственно созданные структуры с необычными свойствами, которые зависят не только от состава материала, но и от микроархитектуры и пространственной организации элементарных ячеек. Сегодня область механических метаматериалов очень широка и включает материалы с отрицательным [1] и нулевым коэффициентом Пуассона [2], отрицательной жесткостью [3], отрицательной сжимаемостью [4] и другими свойствами [5]. Значительный прогресс в 3D-печати как на микро-, так и на макроуровне сыграл ключевую роль в развитии этой области. Возможность создавать сложные конструкции метаматериалов является одним из самых перспективных преимуществ аддитивного производства.

Метаматериалы с отрицательным коэффициентом Пуассона, также известные как ауксетичные материалы, являются наиболее изученным типом механических метаматериалов [2; 6–9]. Они расширяются в поперечном направлении при продольном растяжении и сжимаются при сжатии. Этот механизм деформации эффективно обеспечивает высокую ударную прочность [10– 13], поглощение энергии [6; 14], и сопротивление сдвигу [15]. Благодаря этим преимуществам ауксетичные метаматериалы имеют большой потенциал в различных областях, особенно в авиации [16], спортивных приложениях [17], электронике [18], автомобильной промыш- ленности [19], биомедицинской инженерии [20] и других. Создание ауксетичных структур с различными формами и управляемым механическим поведением может быть основано на широком спектре конструкций ауксетичных ячеек, включая повторно-входящие [6; 14], хиральные [21–23], двойная стрелка [24] и другие типы ячеек.

Существуют различные варианты цилиндрических ауксетичных структур. Например, осесимметричные ауксетики могут быть образованы вращением изогнутой ауксетичной элементарной ячейки [25–30]. В настоящее время в опубликованных работах осесимметричные ауксетики в основном испытывались под осевым сжатием [31] или ударной нагрузкой [32]. Также были проведены испытания свойств ауксетиков, заключенных в цилиндр путем перемещения ячеек в окружном и осевом направлениях при осевой нагрузке [33–35]. Для улучшения механических свойств цилиндры из ауксе-тичных материалов заполнялись различными наполнителями [36]. Другим направлением исследований стали цилиндрические сэндвич-панели с ауксетичными сердечниками [37–40]. Существует также отдельный широкий класс ауксетиков среди материалов с кубической анизотропией [9].

Однако механическое поведение цилиндрических ауксетиков, у которых ауксетичная плоскость перпендикулярна оси цилиндра, практически не изучено. В данной работе исследуются новые конструкции аук- сетичных цилиндров, основанные на повторно-входящей ячейке в плоскости цилиндра. С помощью заданного алгоритма соединения вершин ауксетичной ячейки формируется структура, называемая ауксетичным кольцом, которое затем перемещается вдоль оси Z на несколько слоев с необходимым расстоянием между ними для получения пористого ауксетичного цилиндра. Также, обеспечивается геометрический градиент ауксетич-ного цилиндра от внутреннего радиуса до внешнего радиуса.

Целью работы является изучение механического отклика ауксетичного цилиндра с элементарной ячейкой в плоскости при приложении механической нагрузки и воздействии температуры, а также оценка деформации в плоскости ауксетичности в зависимости от коэффициента термического расширения материала решетки. Цилиндр, состоящий из двух плоских окружных ауксетичных слоев, соединенных вертикальными распорками, моделировался численно с использованием метода конечных элементов. Проведено сравнение с полым цилиндром, обладающим эффективными ауксе-тичными свойствами, рассчитанными на основе анализа регулярной повторно-входящей решетчатой структуры.

Геометрические и механические модели

Геометрия ауксетичного цилиндра основана на повторно-входящей ячейке, расположенной в плоскости цилиндра, со следующей комбинацией параметров: a / b = 1, 0 = 14° (рис. 1). Трехмерная модель элементарной ячейки была разработана в Wolfram Mathematica путем определения координат решетки и порядка их соединения на основе запрограммированного алгоритма. Структурные элементы повторно-входящих ячеек были сформированы цилиндрами (распорками) и сферами (соединительными элементами).

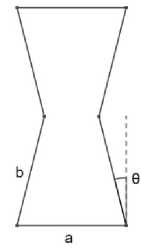
Рис. 1. Ауксетичная элементарная ячейка с осевой ориентацией

Fig. 1. Auxetic unit-cell with axial orientation

Размер отдельной ячейки, а также структурных элементов, можно контролировать путем установки соответствующего масштабирующего коэффициента. В качестве примера рассматривался цилиндр, состоящий из 9 ячеек на внутренней окружности, 4 рядов ячеек в радиальном направлении и 5 окружностей вдоль оси Z (рис. 2).

Также был исследован эффективный твердотельный цилиндр с ауксетичными свойствами, сохраняя геометрические параметры в соответствии с ауксетичным цилиндром. Эти свойства были определены путем анализа механического отклика решетчатой структуры на основе повторно-входящей элементарной ячейки с осевой ориентацией. Размер решетки составлял 30,9 мм × 30,9 мм × 3,9 мм, количество ячеек вдоль оси Y , количество столбцов вдоль оси X и количество рядов вдоль оси Z было: 7 × 5 × 1 (рис. 3) [41].

Z

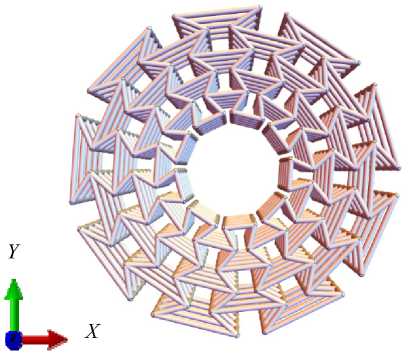
Рис. 2. Многослойный ауксетичный цилиндр

Fig. 2. Multilayer auxetic cylinder

Z

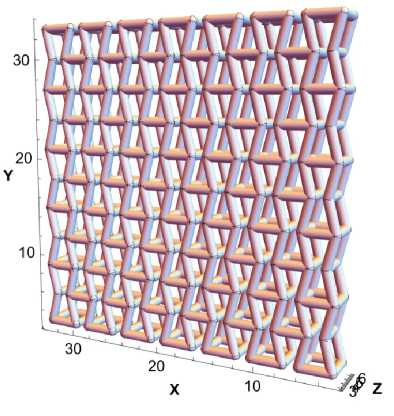
Рис. 3. Пористая повторно-входящая ауксетичная решетка

Fig. 3. Porous re-entrant auxetic lattice

В рамках этого исследования было применено два метода дискретизации с помощью метода конечных элементов. Конечно-элементная модель ауксетичной решетки была создана с использованием инструментов генерации сеток OpenCASCADE, интегрированных в Wolfram Mathematica. Этот метод позволяет создавать 2D-триангуляции для структур типа Boolean, которые впоследствии могут служить основой для тетраэдрической объемной сетки. Однако для дискретизации ауксе-тичного цилиндра этот подход слишком вычислительно затратен как с точки зрения генерации сетки, так и количества конечных элементов. Для решения этих проблем была разработана процедура разбиения сеткой в два этапа. На первом этапе обе фазы разбиваются сеткой с использованием регулярной сетки на основе вок-селей, стандартной техники для анализа конечных элементов структур со сложной геометрией. Значительным недостатком воксельных сеток является наличие острых краев вдоль границ из-за кубической формы вокселей. Чтобы получить более плавную тетраэдрическую сетку, на втором этапе к обеим фазам воксельной сетки применялся алгоритм Dual Marching Cubes, также реализованный в Wolfram Mathematica. Этот итерационный алгоритм предназначен для создания плавных разделяющих поверхностей для двоичных дискретных объемов, часто генерируемых алгоритмами сегментации [42; 43]. Затем конечно-элементные модели были перенесены в SIMULIA Abaqus Standard для численного анализа.

Для анализа деформационного поведения ауксетич-ных структур были сделаны следующие предположения:

• 1.    Изотропный материал: Материал обладает однородными свойствами во всех направлениях.

• 2.    Сплошная структура: Материал решетчатой структуры рассматривается как сплошной, без каких-либо зазоров или пустот.

С учетом этих предположений задача определения деформационного поведения ауксетичных структур может быть сформулирована следующим образом:

V-ст = 0,(1)

£ = 2 (Vu + uV), где σ – тензор напряжений, ε – тензор деформаций. Тепловая упругость моделируется с помощью дополнительного тензора деформации еT :

е = еe + еT,(3)

3v1 +v

£e = Se : ст = —al +----ст,(4)

EE еT = аДTI,(5)

где a = -tr ( ст ) (ур. 4) среднее нормальное напряжение тензора напряжений; а - коэффициент термического расширения (КТР), измеряемый в [1/°C], который показывает, насколько материал расширится или сократится на каждый градус изменения температуры; Ι – единичный тензор второго порядка; Д T = T - T 0 , где T - температура тела в [°C] и T 0 – температура, при которой материал считается находящимся в своем «ненапряженном» состоянии, то есть без термического расширения или сжатия.

Для численного моделирования ауксетичных структур использовалась искусственная модель материала, в которой изменялись коэффициенты термического расширения. Эти характеристики материала представлены в таблице.

Характеристики материала

Material properties

Плотность, т/мм3	1,25 ⋅ 10-9
Модуль Юнга, МПа	2620
Коэффициент Пуассона	0,36
Коэффициент термического расширения [1/°C], 10-5	1,70
	0,34
	0,68
	1,70
	3,40
	6,80

Результаты и дискуссия

Чтобы отдельно изучить термическую составляющую деформации ауксетиков под воздействием нагрева, был рассмотрен частный случай теплового расширения ауксетичной решетки. Граничные условия были заданы следующим образом: перемещение вдоль оси Y было ограничено для верхней и нижней поверхностей. Температурное нагружение 200 °C было приложено ко всей структуре (рис. 4).

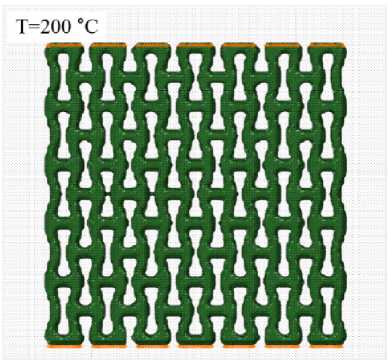
Рис. 4. Граничные условия для нагрева ауксетичной решетки: перемещение верхней и нижней поверхностей вдоль оси Y ограничено

Fig. 4. Boundary conditions for heating of the auxetic lattice: movement of top and bottom faces along the Y-axis was restricted

Линейная зависимость поперечной деформации, измеренной вдоль оси X , от коэффициента термического расширения показана на рис. 5. Для получения поперечной деформации измеряется первоначальная ширина решетки вдоль отмеченной линии AB и ее изменение после приложения нагружения.

График показывает, что при изменении КТР в пределах определенного диапазона значений поперечная деформация увеличивается пропорционально. Рост значения КТР способствует поперечному расширению решетчатой структуры при нагреве, увеличивая ее ауксе-тичность, т.е. степень расширения при механическом нагружении. Это можно использовать как дополнительный механизм управления эффективным механическим откликом, как показано далее.

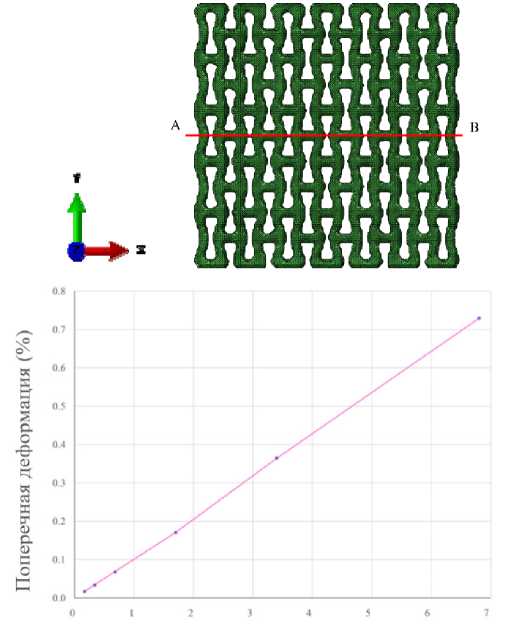
KTP X1Q-5(1/°C)

Рис. 5. Зависимость поперечной деформации (линия AB) от КТР при приложенной температуре 200 ℃

Fig. 5. Dependence of transverse strain (line AB) on the coefficient of thermal expansion under the applied temperature of 200 ℃

Рассматривался случай комбинированной нагрузки, включающий в себя нагрев и растягивающее перемещение: структура нагревалась до 200 °C, а к верхней поверхности прикладывалась растягивающая нагрузка 0,5 мм, при этом нижняя поверхность была закреплена вдоль оси Y (рис. 6).

Зависимость структурного коэффициента Пуассона (измеренного вдоль линии AB – по середине решетки) от КТР показана на рис. 7. Коэффициент Пуассона уменьшается с увеличением коэффициента термического расширения при условии, что растягивающее перемещение и температура остаются неизменными. Дополнительно для иллюстрации концепции представлен график, показывающий приложение только растягивающего перемещения.

При сравнении графиков для растягивающего перемещения и комбинированной термомеханической нагрузки очевидно, что нагрев значительно влияет на структурный коэффициент Пуассона. Приложение дополнительной температурной нагрузки может привести к снижению структурного коэффициента Пуассона в диапазоне от 6,3 до 100 %. Кроме того, анализируя гра- фик, полученный для случая нагрузки и нагрева ауксе-тичной решетки, было обнаружено, что увеличение коэффициента теплового расширения (КТР) в 10 раз по отношению к выбранному начальному значению 1,7 ⋅ 10-6 1/°C привело к значению КТР 1,7 ⋅ 10-5 1/°C и уменьшению коэффициента Пуассона на 18,5 %. Когда значение КТР было увеличено в 40 раз (КТР = = 6,8 ⋅ 10-5 1/°C), полученное снижение коэффициента Пуассона составило 86,6 %.

Т=200 "С

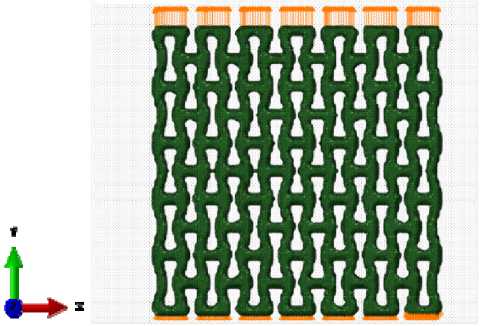
Рис. 6. Граничные условия для одновременного нагрева (200 °C) и растяжения (0,5 мм) ауксетичной решетки с закрепленной нижней поверхностью вдоль оси Y

Fig. 6. Boundary conditions for simultaneous heating (200 °C) and tension of the auxetic lattice (0.5 mm) with constrained bottom face along the Y axis

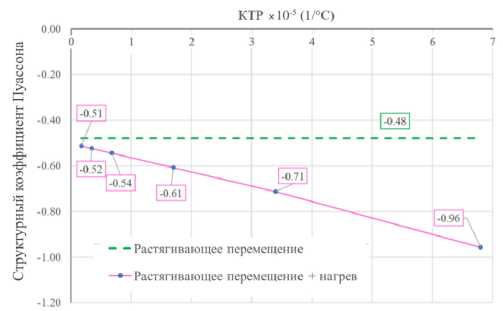
Рис. 7. Зависимость коэффициента Пуассона (линия AB) от КТР при растягивающем перемещении; приложенная температурная нагрузка и растягивающее перемещение

• Fig. 7.    Dependence of Poisson's ratio (line AB) on the coefficient of thermal expansion under tensile displacement; applied temperature load and tensile displacement

Были проанализированы поля распределения перемещений u1 вдоль оси X для температурной нагрузки (рис. 8, а) и для комбинированной нагрузки (рис. 8, b). Полученные результаты демонстрируют положительный комбинированный эффект увеличения КТР матери- ала и ауксетичной структуры на увеличение абсолютной величины отрицательного коэффициента Пуассона решетчатой структуры.

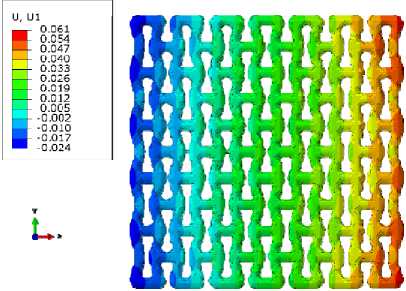
а

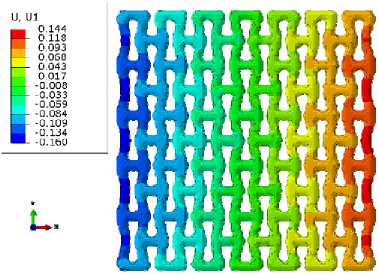
b

Рис. 8. Поля распределения перемещения вдоль оси X при приложении ( а ) температуры и ( b ) температуры и растягивающего перемещения

• Fig. 8.    Fields of displacement distribution along the X -axis applying ( a ) temperature and ( b ) temperature and tensile displacement

Также было изучено влияние изменения КТР материала на структурную деформацию ауксетичных цилиндров. Геометрия и свойства материалов структур соответствовали моделям, представленным в предыдущем разделе. Геометрические размеры цилиндров были следующими: внешний радиус 14,2 мм, внутренний радиус 4,6 мм и высота 10,4 мм. Комбинированный термомеханический отклик ауксетичных цилиндров представлял интерес в связи с потенциальной возможностью управления их деформированным состоянием. Были рассмотрены два случая нагрузки: внутреннее равномерное распределенное давление с фиксированной внешней поверхностью и внешнее распределенное давление с фиксированной внутренней поверхностью. Значение распределенного давления было эквивалентно силе 100 Н. В обоих случаях механическая нагрузка дополнялась тепловым равномерным нагревом до температуры 200 °C, как в ранее рассмотренных случаях (рис. 9).

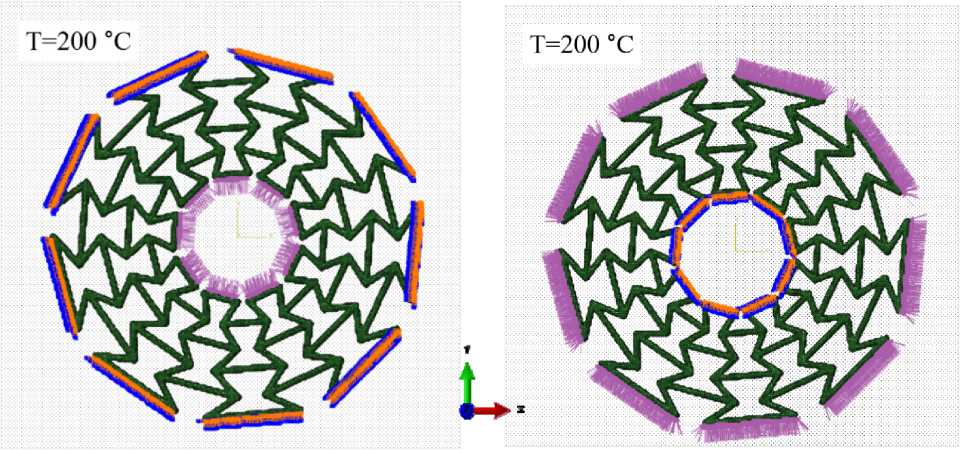
b

а

Рис. 9. Комбинированное нагружение ауксетичного цилиндра: ( а ) внутренне давление и равномерный нагрев, ( b ) внешнее давление и равномерный нагрев

Fig. 9. Combined loading of an auxetic cylinder: ( a ) internal pressure and uniform heating, ( b ) external pressure and uniform heating

Проводилось несколько измерений толщины цилиндра (разность между внешним и внутренним радиусами цилиндра): два измерения вдоль оси X в положительном и отрицательном направлениях, а также вдоль оси Y относительно центра (оси) цилиндра. Из четырех измеренных вариантов использовалось среднее значение для получения радиальной деформации цилиндра, то есть изменения толщины цилиндра относительно первоначального значения (рис. 10).

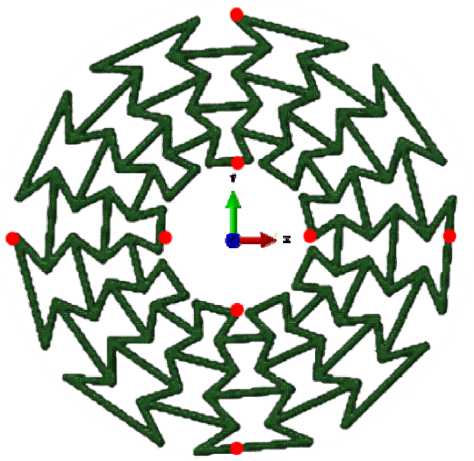
Рис. 10. Толщина цилиндра находится между красными точками

• Fig. 10.    Cylinder thickness is located between red dots

Получены графики, иллюстрирующие зависимость радиальной деформации (в процентах) от коэффициента термического расширения. На них показано, расшири- лась ли структура (значение по оси Y больше 0) или сжалась (значение по оси Y меньше 0) при изменении КТР. Оба графика имеют схожую тенденцию: влияние термического расширения начинает преобладать, при- водя к расширению цилиндра, несмотря на приложен-

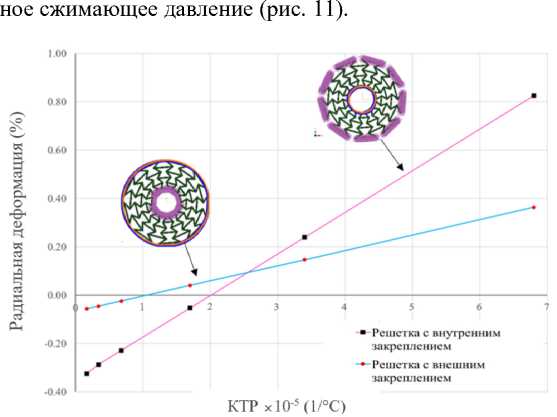
Рис. 11. Зависимость радиальной деформации цилиндра от КТР при двух вариантах приложенной механической нагрузки и температуре 200 °C

• Fig. 11.    Dependence of the radial strain of the cylinder on the CTE under two cases of the applied mechanical load and temperature of 200 °C

Полученные зависимости не похожи в случаях внутреннего и внешнего приложенного давления. Из-за градиента размера ячеек (увеличение размера ячеек от внутреннего диаметра к внешнему диаметру) ауксетич-ный цилиндр деформируется значительнее при приложении внешнего давления. Начальная точка графика ниже (значение деформации в 5 раз меньше), чем для случая приложения внутреннего давления. По мере увеличения КТР его влияние на деформационное поведение в условиях сложного нагружения также увеличивается. Под действием температуры ауксетик с фиксированной внутренней поверхностью деформируется значительнее (приблизительно на 130 % разница в деформации), по сравнению со случаем с фиксированной внешней поверхностью.

Для обоих рассмотренных случаев нагружения радиальная деформация при более низких значениях КТР (менее 1,1·10-5 1/°C для фиксированной внешней поверхности и менее 2,0·10-5 1/°C для фиксированной внутренней поверхности) была меньше нуля, что означает, что приложенное давление оказывало влияние сильнее, чем термическое расширение при нагревании, заставляя ауксетичный цилиндр сжиматься. Точка перехода, когда термические и механические деформации находились в равновесии, наблюдалась при значении КТР 1,1·10-5 1/°C и 2,0·10-5 1/°C соответственно, для ауксетичного цилиндра с фиксированными внешней и внутренней поверхностями. При коэффициенте термического расширения (КТР) 2,6·10-5 1/°C графики пересекаются, указывая, что оба сценария демонстрируют одинаковое значение деформации, приблизительно 0,1 %.

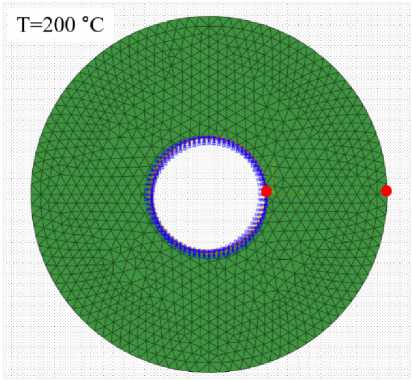
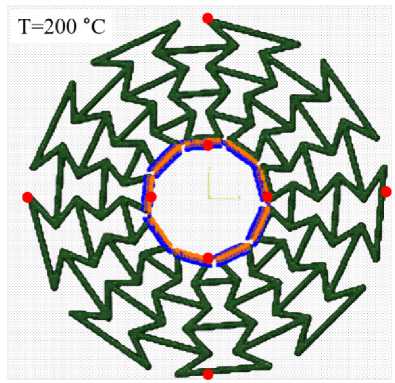
Кроме того, был проанализирован характер поведения ауксетичного цилиндра и сплошного цилиндра с эффективными ауксетичными свойствами при равномерном нагревании, приложенном ко всему объему аук-сетичной решетки и эффективного цилиндра. Перемещения внутренней поверхности были ограничены (рис. 12). Изучено влияние изменения КТР материала на радиальную деформацию цилиндров.

В численном моделировании цилиндров с эффективными свойствами упругие константы материала задавались как ортотропная модель материала (уравнения 6 и 7). Ортотропия эффективных свойств заключается в том, что эффективный сплошной цилиндр имеет различные свойства в трех перпендикулярных направлениях, так как свойства ауксетичной решетки также различны. Необходимые девять независимых параметров упругой жесткости D были получены из результатов численных расчетов растяжения и сдвига решетчатой ауксетичной структуры (рис. 3) в разных направлениях декартовой системы координат. Проведены расчеты на растяжение для получения модулей Юнга (E1, E2, E3) вдоль трех перпендикулярных осей (1 – ось X, 2 – ось Y, 3 – ось Z). Также были определены структурные коэффициенты Пуассона ν12 , ν21 , ν23 , ν32 , ν13 , ν31 , где первый индекс – направление поперечной деформации, второй индекс – направление, вдоль которого прикладывается продольное нагружение. Например, коэффициент Пуассона решетчатой структуры ν12 был рассчитан по формуле (9), где ε11 – поперечная деформация, ε22 – продольная деформация. По результатам расчетов на сдвиг получены модули сдвига G23, G31, G12, индексы обозначают плоскость, в которой происходит сдвиг. Полученный тензор представлен в уравнении (10). Матрица ортотропных свойств был назначена конечным элементам сплошного цилиндра с учетом вращения локальной системы координат.

а

b

Рис. 12. Температурное нагружение (200 ℃) с закрепленной внутренней поверхностью: ( а ) эффективный и ( b ) решетчатый ауксетичный цилиндры

Fig. 12. Temperature loading (200 ℃) with fixed inner surface: ( a ) effective and ( b ) lattice auxetic cylinders

^ 1 ’		Д 111   D 1122   D 1133     0      0      0	Г6 1 1
σ 2		D 2211   D 2222   D 2233     0      0      0	^ 2
σ 3	=	D 3311   D 3322   D 3333    0      0      0	6 3	,(6)
σ 4		0     0      0     D 2323    0     0	6 4
σ 5		0      0      0      0     D 1313    0	6 5
° 6 _		_ 0      0      0      0      0     D 1212 _	_6 6 _

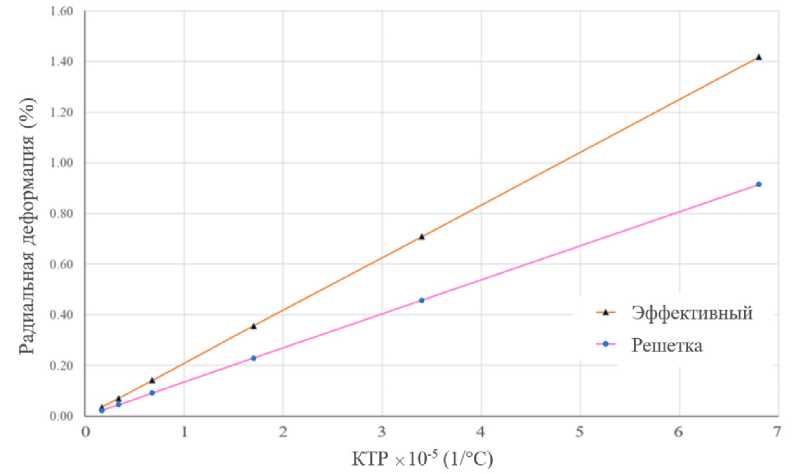
Рис. 13. Зависимость радиальной деформации цилиндра от значения КТР при нагревании до 200 ℃ при фиксированной внутренней поверхности для эффективного и решетчатого ауксетичного цилиндра

Fig. 13. Dependence of the radial strain on initial value of CTE under heating of 200 ℃ with fixed inner surface for effective and auxetic lattice cylinder

" 1-V23V32    V21 +V23V31 V31 +V21V32    0     0     0 ’ E2 E3Л      E2 E3Л      E2 E3Л V21 +V23V31    1-V13V31    V32 +V12V31    0     0     0 E2 E3Л      E1 E3Л      E1 E3Л , (7) D = V31 +V21V32   V32 -V12V31    1-V12V21     0    0    0 E2 E3Л      E1 E3Л      E1 E2 Л 0            0            0       G23   0    0 0            0            0        0   G31   0 0            0            0        0    0   g12 где

Л =	( 1 -V 12 V 21 - V 23 V 32 - V i 3 V 3 i - 2 v 2i V 32 V i3 ) / ( E i E 2 E 3	. (8)
	V 12 = -e ii / e 22 ’	(9)
	" 614.55 - 6.01   37.74     0       0       0 ’
	- 5.02 106.88   2.01      0      0      0
	37.28   7.09 623.96    0      0      0
D =		.(10)
	0       0       0    113.39    0      0
	0       0       0       0    13.82    0
	_ 0        0        0        0       0    110.07 _

Зависимость радиальной деформации цилиндров от КТР для эффективного и ауксетичного цилиндров представлена на рис. 13.

График, описывающий механическое поведение цилиндра с эффективными ауксетичными свойствами, не соответствует графику решетчатого цилиндра. Это указывает на то, что предлагаемая ортотропная модель материала не отражает структурные деформации решетчатого ауксетичного цилиндра, и для понимания основного деформационного поведения требуется явное моде- лирование решетки. Однако для обеих моделей сохраняется одинаковая тенденция линейного расширения цилиндра с увеличением КТР материала.

Заключение

Проведен ряд численных исследований для изучения комбинированного термомеханического поведения новых ауксетичных структур. Изучалось влияние коэффициента термического расширения на механические характеристики ауксетичных решеток. Их поведение при температурной нагрузке, а также при комбинированной нагрузке (температура и приложенное давление) исследовалось с изменением коэффициента термического расширения и граничных условий. Проведены численные расчеты для определения механических констант для задания ортотропной модели эффективного ауксетичного цилиндра, механический отклик которого также сравнивался с откликом решетчатого ауксетичного цилиндра.

Было показано, что изменения свойств материала, приводящие к изменению КТР, могут значительно влиять на эффективный структурный отклик цилиндров с ауксетичностью в плоскости, что приводит к переходу от сжатия к расширению при сохранении геометрических свойств решетки.

Эти результаты дают ценную информацию о термомеханическом поведении ауксетичных структур и предполагают их потенциал в качестве перспективных материалов для инженерных применений, требующих контролируемого термомеханического отклика, особенно в конструкциях, подверженных механическим и термическим деформациям.