Влияние изменения кривизны преломляющих поверхностей глаза на качество изображения на сетчатке в модели Лиоу-Бреннана

Известно, что около 80 % информации человек получает с помощью глаз. Глаз имеет сложное строение. Сетчатка содержит фоточувствительные клетки: палочки и колбочки. Они имеют вытянутую форму и в длину составляют около 50 мкм, а радиус примерно равен 2 мкм. Колбочки в основном обеспечивают цветное зрение при хорошем освещении, а палочки более чувствительны и играют важную роль для ориентирования в темноте. Для цветного и сумеречного зрения различные факторы, ухудшающие изображение, на удивление удачно сбалансированы и практически полностью нивелируются у здорового глаза. Размеры чувствительных клеток и расстояние между ними позволяют избавиться от хроматических аберраций, а диафрагмирование радужной оболочкой почти полностью убирает непараксиальные лучи. Однако нарушения геометрии, прозрачности и показателя преломления приводят к значительному ухудшению изображения.

Качество жизни катастрофически снижается с падением уровня зрения. Наука набрала огромный опыт в борьбе с глазными болезнями, который показал, что основной проблемой являются возрастные изменения в оптической системе глаза, которые можно оценить через волновые аберрации. Заметим, что эти искажения индивидуальны не только для отдельных людей, но и для каждого глаза даже в различное время суток.

Волновые аберрации глаза могут быть измерены с помощью различных субъективных и объективных методов. Субъективные методы основаны на сборе визуальных ответов пациента, в то время как объективные методы не требуют сотрудничества пациента и основываются на записи изображений после двойного прохода через окуляр. Среди методов, разрабатываемых в течение многих лет, метод выравнивания [1], аберроскопия [2], метод ножа Фуко [3], восстановление фазы по изображению сетчатки [4].

Существующие клинические аберрометры обеспечивают достаточно точные измерения отклонения волнового фронта глаза [5–7]. При этом измеряются аберрации высокого порядка, позволяющие оценить индивидуальные отклонения волнового фронта, в том числе связанные с профессиональной деятельностью или возрастными изменениями, с целью оптимизации оптической (контактными или внутриглазными линзами) или хирургической коррекции человеческого глаза.

Наиболее широко используемым сегодня методом измерения аберраций глаза является датчик волнового фронта Хартмана–Шака (Hartmann–Shack) [8].

Заметим, однако, что общепринятым представлением волнового фронта является ряд полиномов Цер-нике, которые соответствуют различным аберрациям волнового фронта [9, 10]. Коэффициенты разложения волнового фронта по ортогональным полиномам Цернике позволяют определить среднеквадратическую ошибку отклонения от идеального фронта. Коэффициенты с высоким абсолютным значением автоматически указывают на те аберрации, которые наибольшим образом искажают волновой фронт в индивидуальной системе зрения и, таким образом, позволяют существенно ускорить и упростить анализ зрения пациента [11, 12].

Большие возможности по исправлению оптических характеристик глаза даёт лазерная коррекция зрения [13]. Данная операция заключается в лазерной абляции тканей роговицы с целью улучшения оптических характеристик. Наиболее щадящим является метод LASIK, при котором сохраняется оптически гладкий передний слой роговой оболочки. При этом значительно сокращается послеоперационный период и риск осложнений, как если бы абляция производилась вместе с передним слоем роговицы.

Важной задачей является расчёт индивидуального профиля абляции. Некоторые факторы, которые необходимо учитывать: толщина роговицы, минимизация высоты абляционного профиля [15], заболевания и помутнения роговицы (кератоконус), возможные изменения формы роговицы в силу изменения механических свойств. Корректирующий профиль рассчитывается по данным диагностического оборудования.

В качестве примера приведём следующие диагностические приборы.

• 1.    Окулайзер [16], строящий топографию передней глазной камеры (роговицы, водянистой влаги, радужки, передней поверхности хрусталика). При применении мидриатиков возможно получение топографии задней поверхности хрусталика. Для вычисления оптической силы роговицы используется модель Гульстранда.

• 2.    Тополайзер [17]. Измеряет топограмму передней поверхности роговицы.

• 3.    Двухпроходный аберрометр на основе датчика Шака–Хартмана.

При этом необходимо продолжать совершенствовать как способы проектирования и производства внешней оптики, так и методологию интраокулярной имплантации и хирургической коррекции различных глазных заболеваний и травм.

Для решения данных задач предложено несколько оптических моделей глаза [18–20], включающих в себя несколько десятков параметров преломляющих поверхностей и тканей глаза. Наиболее часто встречающейся в литературе является модель, разработанная Лиоу и Бреннаном в 1997 году [18]. Главным нововведением учёных является учёт градиентного показателя преломления хрусталика. Однако продолжает использоваться и простая модель Гульстранда [19], в которой все поверхности считаются сферическими, а показатели преломления сред – постоянными. В настоящее время оптики ведут исследования с целью улучшения существующих моделей глаза путём введения особых асферик на различные поверхности [20, 21], учёта современных биометрических измерений.

Одной из основных задач является выбор параметров модели глаза по данным офтальмологического исследования пациента [20]. Полученные диагностические данные позволяют оценить качество изображения, получаемого глазом, поставить диагноз и рекомендовать метод лечения.

Цель данной работы заключается в исследовании с помощью пакета Zemax влияния искажения различных преломляющих поверхностей на качество изображающей системы глаза, точнее только роговицы. В качестве модели глаза выбрана модель с градиентным хрусталиком Лиоу–Бреннана.

Описание модели

На рис. 1 показана условная схема глаза, поясняющая ход лучей при формировании изображения.

В данной работе использовалась одна из наиболее часто применяемых современных моделей – модель Лиоу–Бреннана [18]. Она учитывает смещение зрачка относительно оптической оси, кривизну поверхности сетчатки, медиально-направленное положение глаза. Хрусталик полагается дублетом двух градиентных линз с градиентным профилем показателя преломления. Для каждой из двух линз – частей хрусталика – выбираются свои параметры профиля показателя преломления и кривизн преломляющих поверхностей.

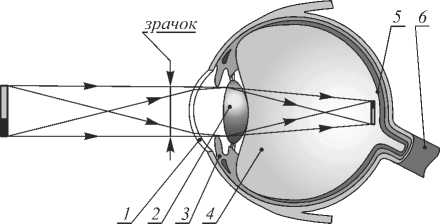
Рис. 1. Схема формирования изображения в глазу:

1 – роговица, 2 – хрусталик, 3 – радужная оболочка,

4 – стекловидное тело, 5 – сетчатка, 6 – зрительный нерв

Для моделирования использовался программный пакет Zemax. Частичное описание модели можно найти в [22]. Согласно модели Лиоу–Бреннана (рис. 2) глаз имеет 6 преломляющих поверхностей и сферическую поверхность сетчатки, на которой формируется

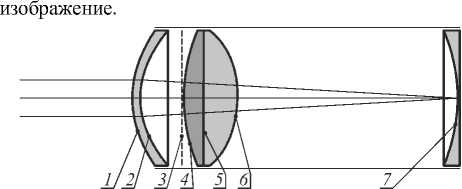
Рис. 2. Схема расположения преломляющих поверхностей глаза в рассматриваемой модели: 1 – передняя поверхность роговицы, 2 – задняя поверхность роговицы, 3 – радужная оболочка со зрачком, 4 – передняя поверхность хрусталика, 5 – граница раздела составных поверхностей хрусталика, 6 – задняя поверхность хрусталика, 7 – сетчатка

В табл. 1 приведено описание каждой поверхности, отмеченной на рис. 2. В рассматриваемой модели предлагается описывать профиль показателя преломления хрусталика с помощью следующего полинома.

n = n 0 + n r 2 r ² + n_z 1 z + n_z 2 z 2 ,                          (1)

где ( r , z ) – цилиндрические координаты, z – оптическая ось, n 0 , n r 2 , n z 1 , n z 2 – коэффициенты полинома.

Моделирование искривления поверхности роговицы

В данной работе исследовалось влияние внесения полинома Цернике в кривизну передней эллиптической поверхности роговицы. Для расчётов использовался программный пакет Zemax.

Полиномы Цернике выражаются следующей формулой. Чётный полином: Zn (p, ф) = Rn (p) cos (mф), нечётный полином: Z-m (p,ф) = Rn (p)sin(mф), где n - m

Rm (p)=s k=0

^{(- 1 )} k ⁽ n ^- к ^{) !}

,,( n + m ,Yf n - m , к ! - к ! - к

I 2 JI 2

p n - 2 к

Табл. 1. Параметры оптической схемы глаза в модели Лиоу–Бреннана

№ поверхности	Описание	Радиус кривизны (мм)	Параметр кривизны Q = - e 2, e — эксцентриситет	Расстояние до следующей поверхности (мм)	Показатель преломления	Коэффициент дисперсии n D - 1 nF - n^ FC	Радиус апертуры (мм)
1	Передняя поверхность роговицы	7,77	–0,18	0,55	1,376	50,23	5
2	Задняя поверхность роговицы/Передняя поверхность водянистой влаги	6,4	–0,6	3,16	1,336	50,23	5
3	Радужная оболочка со зрачком (находится в водянистой влаге)	^	0,0	0,0	1,336	50,23	1,25
4	Задняя поверхность водянистой влаги / Передняя поверхность хрусталика	12,4	0	1,59	Коэффициенты полинома n 0 = 1,368, n r 2 = –0,001978, n z 1 = 0,04957, n z 2 =–0,015427		5
5	Граница раздела составных частей хрусталика	^	0	2,43	Коэффициенты полинома n 0 = 1,407, n r 2 = –0,001978, nz 2 = –0,006605,		5
6	Задняя поверхность хрусталика / Передняя поверхность стекловидного тела	–8,1	0,96	16,23883	1,336	50,23	5
7	Задняя поверхность стекловидного тела / Сетчатка	–12	0				5

Аберрации волнового фронта могут быть представлены с помощью полиномов Цернике. Так:

дефокусировка: Z 2 ( р , ф ) = (2 р ² - 1), сферическая аберрация 3-го порядка:

Z40 (р, ф) = (6р4 - 6р2 + 1), дисторсия: Z 1 (р, ф) = р cosф , кома: Z3 (р, ф) = (3р3 - 2р)cosф, астигматизм Z2 (р, ф) = р2 cos2ф .

Форма передней поверхности роговицы моделировалась многочленом из полиномов Цернике:

z ( Г , ф ) =

cr

1 + 1 - - ( 1 + k ) c ² r²

N

+E AZ (р, ф),

i = 1

где c – кривизна поверхности (обратная величина радиуса), k - коническая постоянная ( k = - £ ², где £ – эксцентриситет, гиперболоид вращения будет при k < –1, параболоид – при k = –1, эллипс – для –1 <  k < 0, сфера для k = 0), N – количество полиномов Цернике, Z i ( р , ф ) - i -й полином Цернике (2), A_i – вес i -го полинома Цернике, r – радиальная координата, ф - угловая координата, р = r / R -нормированная координата луча, R – р адиус нормировки. Подробнее в руководстве пользователя Zemax [23].

N

Ряд в формуле (3) ∑ A i Z i ( р , ф ) - так называемый i = 1

ряд Аризонского университета [24]. Члены с наименьшими индексами соответствуют аберрациям волнового фронта низких порядков, которые мы и рассматриваем. Выбор индексов соответствует следующим выражениям

Z 1 = Z 0 ( р , ф ) , Z 2 = Z 1 ( р , ф ) , Z 3 = Z 1 ^{- 1} ( р , ф ) ,

Z 4 = Z 2 ( р , ф ) , Z 5 = Z 2 ( р , ф ) , Z 6 = Z - 2 ( р , ф ) ,

Z 7 = Z 3 ( р , ф ) , Z 8 = Z 3 ^{- 1} ( р , ф ) , Z 9 = Z 0 ( р , ф ) .

Итак, моделируем искривление передней поверхности роговицы (номер 1 на рис. 1) с помощью (3) и находим коэффициенты аберраций волнового фронта в изображении, также выраженные в полиномах Цер-нике. Заметим, что коэффициенты аберраций Зайделя не вычисляются в пакете Zemax. Но, например, в [25] можно найти соответствие полиномов Цернике различным типам аберраций Зайделя.

В табл. 2 представлены аберрации, которыми обладает глаз в рассматриваемой модели для различных изменений параметров преломляющих поверхностей и сред глаза. В первой строке приведены аберрации модели, взятой без изменений из статьи [22]. Нетрудно видеть, что данная модель обладает существенными аберрациями, диаграмма рассеяния точки представлена на рис. 3.

Табл. 2. Зависимость аберраций Зайделя оптической системы глаза от искривления передней поверхности роговицы

Изменение в модели глаза	Дефокусировка	Сферическая аберрация	Дисторсия	Кома	Астигматизм
Исходная модель из [22] без изменений	0,074349	0,019130	-0,074324	-0,035601	0,075212
Уменьшение толщины роговицы на 50 мкм	0,001940	0,018831	-0,072308	-0,034599	0,076402
К кривизне поверхности 1 (рис. 2) добавлен многочлен 0,0015(2 y 2–1)	0,075532	0,019136	-0,076079	-0,036485	0,000604
Комбинация изменений из двух предыдущих строк	0,003110	0,018832	-0,074055	-0,035457	0,002082
Радиус кривизны поверхности 1 (рис. 2) увеличился на 0,4 мм с 7,77 мм до 8,17 мм	-1,938216	0,012932	-0,077931	-0,037565	0,099983
Радиус кривизны передней поверхности роговицы равен 8,17, как в предыдущей строке, а радиус задней поверхности роговицы (строка 2 из табл. 1) увеличен с 6,4 до 6,8	-1,647906	0,012724	-0,066153	-0,031674	0,091476
Хрусталик сделан с постоянным показателем преломления n 5 = 1,368, n 6 = 1,407 (первые коэффициенты в полиноме 1)	-6,431658	0,076361	-0,278492	-0,139330	0,098098
Хрусталик выполнен из стекла BK7. Параметры поверхностей подобраны автоматически таким образом, чтобы минимизировать аберрации	0,614030	0,043502	-0,097557	-0,048239	0,069149

б)

^0,4861 ' = 0,5876

25 мкм *

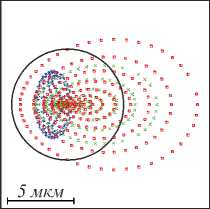
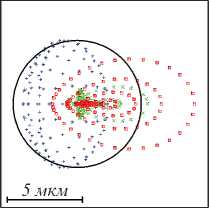
Рис. 3. Диаграмма рассеяния точки при изменении модели глаза, взятой из [22]. Для различных длин (показаны цветами) волн точки пересечения лучей с поверхностью изображения точки показаны разными цветами;

• (а)    неизменённой модели (первая строка табл. 2);

• (б)    модели с тонкой роговицей (вторая строка табл. 2);

• (в)    со стеклянным хрусталиком (последняя строка табл. 2). Чёрным показан кружок Эйри при λ = 587,6 нм

  Из рис. 3 в и табл. 2 (последняя строка) видно, что замена градиентного хрусталика однородным стеклянным телом приводит к увеличению дефокусировки на порядок. Дефокусировка исходного глаза составляет 0,07434936 (строка первая табл. 2). Уменьшение толщины роговицы всего на 50 мкм (вторая строка табл. 2) приводит к уменьшению дефокусировки на 74 %. Аналогично можно скомпенсировать астигматизм на 99 % путём внесения цилиндрического параболоида в переднюю поверхность роговицы (строка 3 табл. 2).

Ничто не мешает комбинировать компенсирующие полиномы с целью единовременного уменьшения астигматизма, а также дефокусировки. Этой цели удалось достигнуть, внеся в кривизну передней поверхности роговицы полинома 0,05* Z ₀⁰ ( ρ , ϕ ) - 0,0015* Z ₂² ( ρ , ϕ ) . Уменьшение дефокусировки при этом составило 58 %, а уменьшение астигматизма – 97 % (строка 4 табл. 2).

Необходимо отметить, что аберрации волнового фронта измеряются в миллиметрах. В офтальмологии определения величины аберраций используются как диоптрии, так и линейные единицы (миллиметры или микроны). В диоптриях обычно измеряется продольная аберрация ∆ с уточнением типа и ориентации аберрации. В миллиметрах или микронах задаётся вес полинома Цернике, определяющего аберрацию волнового фронта W (ρ, ϕ) = ∑Zi (ρ, ϕ) , (Zi (ρ, ϕ) – i-й по лином Цернике). Соответствие между продольной аберрацией и аберрацией волнового фронта можно установить с помощью следующего приближённого соотношения (из [25]):

_{∆ ≈} 1 ∂ W ( ρ , ϕ ) A ² ρ ∂ρ ,

где ( ρ , ϕ ) – зрачковые координаты, А – задняя апертура пучка. Формула (4) является весьма приближённой, так как учитывает только первый член разложения. Поэтому использование весов полиномов Цернике является предпочтительным для измерения аберраций, порядком выше первого.

Заключение

В работе проведено моделирование пакетом Zemax аберраций глаза в модели Лиоу–Бреннана и получены следующие результаты. Утоньшение или утолщение роговицы может приводить к уменьшению аберрации дефокусировки.

При введении параболической зависимости вдоль одной оси (введение астигматизма роговицы) можно уменьшать или увеличивать астигматизм глаза. Изменение кривизны поверхности роговицы может скомпенсировать комбинации аберраций, соответствующие введённым в кривизну полиномам. Причём остальные аберрации остаются неизменными. Изменение радиуса кривизны роговицы существенно влияет на качество изображения. Так, при увеличении радиуса на 400 мкм дефокусировка увеличивается в 200 раз. При замене биологического хрусталика на стеклянный резко возрастают почти все виды аберраций. Заметим, что описание аберраций глаза в полиномах Цернике позволит рассчитать дифракционный оптический элемент для компенсации аберраций глаза, согласно методике, изложенной в [12]. Авторы планируют посвятить этому следующую статью.

Работа выполнена при поддержке Министерства образования и науки РФ и гранта РФФИ 15-29-03823.