Влияние эффектов неравно весности на характеристики теплообмена возвращаемого аппарата "Орёл"

Работа посвящена расчётным исследованиям обтекания и определения конвективных тепловых потоков на поверхности возвращаемого аппарата (ВА) «Орёл» [1] на гиперзвуковых участках движения в атмосфере Земли при возвращении от Луны по траектории с двумя погружениями с учётом влияния реальных свойств газа, в т. ч. при наличии физико-химических процессов в ударном слое и на поверхности аппарата.

Чтобы выявить отличия характеристик теплообмена на поверхности ВА при равновесном и неравновесном течениях в ударном слое, проводится моделирование течения двумя методами решения уравнений Навье–Стокса, реализованными в двух программах.

В первой программе реализован конечно-объёмный метод решения уравнений Навье–Стокса, использующий схему AUSM [2] для численного моделирования равновесных течений около ВА сегментально-конической формы. Метод позволяет проводить расчёты течений совершенного газа и равновесного воздуха.

Во второй программе применён конечно-разностный метод решения уравнений Навье–Стокса, который использует центральные разности с добавлением искусственной диссипации и предназначен для численного моделирования течений совершенного газа, равновесного и неравновесного воздуха. Подробное описание метода содержится, например, в работах [3, 4].

модель неравновесно-диссоциирующего и частично ионизованного воздуха

В данном разделе изложены основные элементы физико-химической модели высокотемпературного неравновесно-диссоциирующего и частично ионизованного воздуха [5], используемые при проведении расчётов обтекания и теплообмена ВА при полёте в атмосфере.

При высоких температурах течение газа (воздуха) сопровождается целым рядом физико-химических процессов. В число этих процессов входят:

• •    неравновесная диссоциация и ионизация;

• •    различные процессы энергообмена между различными степенями свободы (поступательной, вращательной, колебательной, электронной);

• •    многокомпонентная диффузия, теплопроводность;

• •    различные гетерогенные процессы на твёрдых поверхностях, обтекаемых плазмой (аккомодация поступательной и колебательной энергий, рекомбинация атомов и ионов).

Учёт всех этих процессов в рамках решения уравнений Навье–Стокса хотя и возможен, но приводит к слишком громоздкой системе уравнений. Это не позволяет получать необходимые результаты оперативно, даже при наличии современной вычислительной техники. Поэтому в рассматриваемой модели на основе анализа вклада протекающих в высокотемпературном воздухе процессов были сделаны некоторые упрощения, которые в большинстве случаев не снижают точности получаемых результатов.

С целью упрощения описания физикохимической модели воздуха примем следующие предположения:

• 1)    вращательная и колебательная температуры молекул равны поступательной температуре T ;

• 2)    заселённости внутренних уровней энергии частиц (колебательных и электронных) отвечают больцманов-скому распределению с температурой, равной поступательной температуре;

• 3)    поступательная температура электронного газа полагается равной поступательной температуре тяжёлых частиц.

Первое условие может нарушаться только в сильно разреженном газе. Второе условие также не всегда выполняется в разреженном газе. Это необходимо принимать во внимание при расчётах интенсивности неравновесного излучения молекул. В некоторых случаях каждое из электронновозбужденных состояний молекул следует рассматривать как отдельный компонент. Однако это допущение не влияет на точность определения других параметров газа. Третье допущение может нарушаться только вблизи фронта сильных ударных волн или в высокочастотных электромагнитных полях.

В данной модели неравновесного воздуха учитываются 11 химических компонент (O2, N2, NO, O, N, e–, NO+, N2+, O2+, N+, O+), между которыми происходят следующие 10 реакций:

• O₂ + M₁ = O + O + M₁;

N2 + M2 = N + N + M2;

NO + M3 = N + O + M3;

O + N2 = N + NO;

O + NO = N + O2;

O + N = NO+ + e–;

N + N = N2+ + e–;

O + O = O2+ + e–;

N + e– = N+ + 2e–;

O + e– = O+ + 2e–, где М — любая из химических компонент.

Диффузионные потоки i -й химической компоненты определяются согласно закону Фика и, например, в направлении оси x имеют вид:

d = –ρD ∂ci i, x           i ∂x где ρ — плотность газовой смеси; ρi и ci = ρi /ρ — плотность и массовая концентрация i-й химической компоненты, соответственно.

Для определения коэффициентов диффузии Di используется приближение постоянных чисел Шмидта Sci = μ/ρDi, которые принимаются равными 0,75 для нейтральных частиц [5]. Для коэффициентов амбиполярной диффузии ионов используется выражение Di,ion = 2Di [6]. Чтобы сумма диффузионных потоков была равна нулю

∑ d_i = 0,

выполняется

корректировка, предложенная в работе [7]:

d^с = d – c ∑ d .

i , x         i , x         i          i , x

Концентрации химических компонент на поверхности находятся из уравнений массового баланса, которые для атомов и ионов имеют следующий вид:

d_{i , w} + k_{i , w} ρ _i = 0.

В методе применяется модель гетерогенного катализа, основанная на использовании постоянной величины вероятности рекомбинации атомов на поверхности аппарата — γ_А, которая связана с константой скорости каталитической рекомбинации k_w соотношением [5]

2γА ka = i,w    2 – γА

1 RT w

2π M ^;

i

K^ON г , w

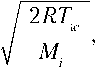
где R — универсальная газовая постоянная; T_w — температура поверхности; M_i — молекулярный вес i -й компоненты. В этом случае значения у А = 0 и у А = 1 соответствуют абсолютно некаталитической и каталитической поверхностям. В расчётах используется величина у А = 0,01, которая отвечает значениям k_w ≈ 4 м/с, что соответствует каталитичностям неразрушающихся высокотемпературных теплозащитных покрытий (ТЗП) при их интенсивном нагреве. Для ионов вероятность поверхностной рекомбинации полагается равной единице. Полный поток тепла q = ( q_x , q_y , q_z ) есть сумма тепловых потоков за счёт теплопроводности и диффузии химических компонент:

∂T q = – κ + hd , x          ∂x           i i,x hi = CpiT + е e ( T) + е vb ( T) + hi, где hi — энтальпия i-й химической компоненты; Cрi — теплоёмкость при постоянном давлении поступательных и вращательных степеней свободы i-й химической компоненты на единицу массы; е e, е vib — энергии электронного и колебательного (для молекул) возбуждения; hfi — энтальпия образования i-й химической компоненты на единицу массы.

Вязкость ц и теплопроводность к смеси находятся по формулам Уилки [8] и Мэйсона–Саксена [9]. На поверхности ставились условия прилипания потока и адиабатичности

• q . = ^е w ° T W >

где е w — коэффициент черноты; ° — постоянная Стефана–Больцмана. Данная модель неравновесного воздуха была протестирована в работах [10, 11].

Параметры расчётных задач

Возвращаемый аппарат космического корабля «Орёл» имеет сегментальноконическую осесимметричную форму. Численные исследования проводились на различных расчётных сетках, общий вид одной из них приведён на рис. 1. Показана структура в плоскости симметрии течения и на поверхности ВА, размер сетки 178×50×57.

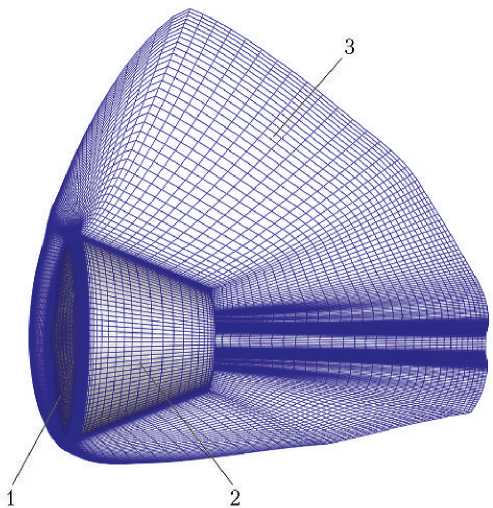
Рис. 1. Общий вид расчётной сетки: 1 — лобовой защитный экран; 2 — боковая поверхность возвращаемого аппарата; 3 — пространственная расчётная сетка

Для подробного анализа структуры течения выбраны две точки траектории — № 1 ( H ≈ 79 км; V _∞ ≈ 10 600 м/с; а = 23°) и № 2 ( H - 74 км; V ~ - 10 800 м/с; а - 26°) по причине заметного влияния эффектов неравновесности течения газа в ударном слое и значительных удельных тепловых потоков.

Расчёт проводился при радиационноравновесной температуре поверхности c коэффициентом черноты поверхности е = 0,85. Для течения неравновесного воздуха вероятность гетерогенной рекомбинации атомов О и N на поверхности у А = 0,01.

результаты расчётов

На рис. 2 приведены картины головных ударных волн, соответствующих установившемуся решению. Красным цветом отмечены результаты расчётов в рамках совершенного газа, зелёным — в рамках модели равновесного воздуха, коричневым — в рамках модели неравновесного воздуха. Больший отход головной ударной волны от поверхности ВА наблюдается для модели обтекания совершенным газом. Различие в отходах головной ударной волны от ВА при расчётах в рамках моделей равновесного и неравновесного воздуха не столь значительно, но всё же имеет место. Наименьший отход наблюдается по модели равновесного воздуха.

Расчёты подтверждают известный эффект [12] — разное положение критической точки на поверхности головного сферического сегмента ВА при расчётах в рамках разных моделей набегающего потока. Рис. 2 демонстрирует этот эффект. На сферическом сегменте ВА показаны положения критических точек, цвета соответствуют расчётным моделям, как для головной ударной волны. Видно, что наибольшие отличия от картины, полученной в рамках модели совершенного газа, даёт модель равновесно-диссоциирующего воздуха. Смещение критической точки при расчётах в рамках модели неравновесно-диссоциирующего воздуха выражено несколько слабее. Ясно, что при этом происходит и смещение зоны максимального давления, и, как следует из этого, изменение значений коэффициента момента тангажа.

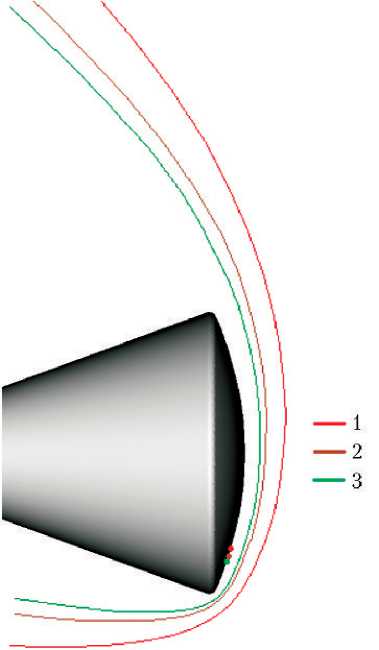
Рис. 2. Положения головного скачка уплотнения и критической точки для случаев обтекания ВА совершенным газом (1), неравновесным воздухом (2) или равновесным воздухом (3)

Структура течения в виде распределения линий тока, полученная по неравновесной и равновесной моделям в точке траектории №1, показана на рис. 3, 4. В неравновесной модели (рис. 3) в донной области течения образуется отрыв. В равновесной модели (рис. 4) течение безотрывное.

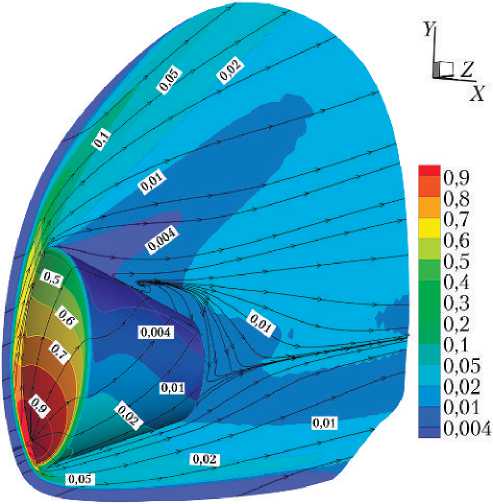
Рис. 3. Картина линий тока и изолиний давления

P = p/ ρ _∞V ² _∞ в плоскости симметрии и на поверхности ВА. Неравновесный воздух. Точка траектории № 1

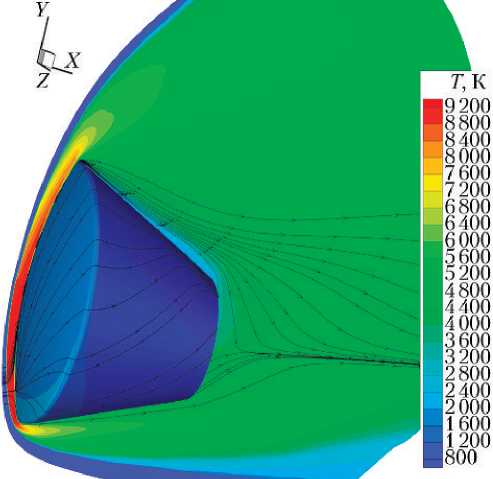
Рис. 4. Картина линий тока и изолиний температуры T(K) в плоскости симметрии и на поверхности ВА. Равновесный воздух. Точка траектории № 1

Характер распределения теплового потока на лобовой поверхности ВА для равновесного и неравновесного воздуха показан на рис. 5. Аналогичное сравнение для боковой и торцевой (донной) поверхностей приведено на рис. 6. На лобовой и боковой поверхностях значение теплового потока для равновесного воздуха всегда больше, чем для неравновесного, на донной поверхности ситуация может быть обратная. Превышение значений теплового потока для случая равновесного обтекания по сравнению с неравновесным обтеканием на большей части лобовой поверхности равно ~10–20%, увеличиваясь к кромке до 40%. На боковой поверхности различие в тепловых потоках составляет ~20–50%, также увеличиваясь к кромке.

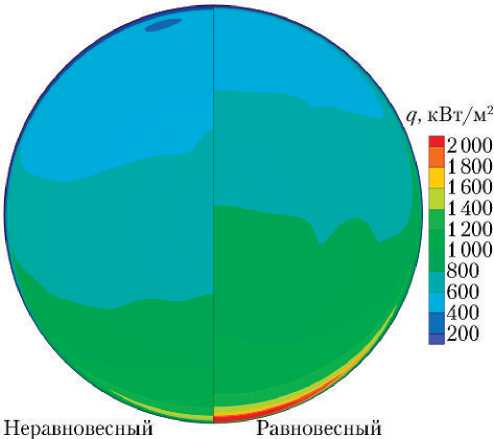
Рис. 5. Тепловой поток на лобовой поверхности ВА для неравновесного и равновесного воздуха. Точка траектории № 2

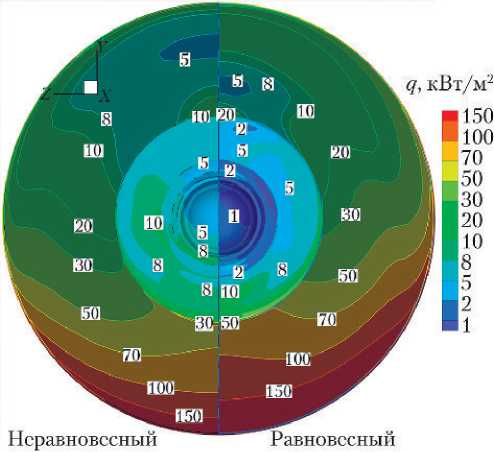
Рис. 6. Распределение тепловых потоков на донной поверхности ВА для неравновесного и равновесного воздуха. Точка траектории № 2

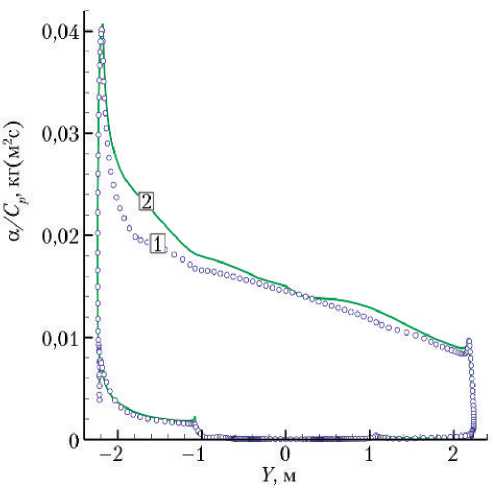
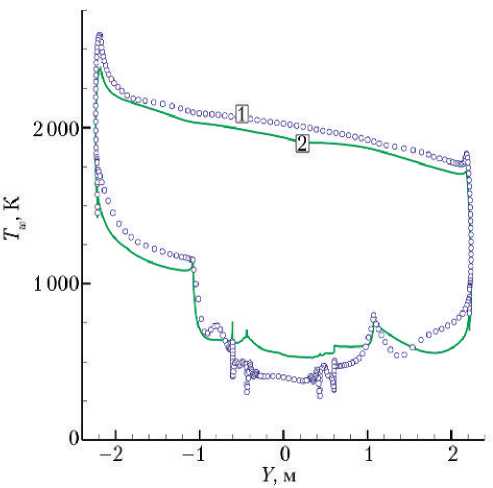
Сравнение (для случаев равновесного и неравновесного обтеканий) значений тепловых потоков q_w , коэффициента α/ C_p и равновесной радиационной температуры поверхности T_w в плоскости симметрии приведено на рис. 7, 8. Можно видеть, что на лобовом щите ВА наблюдаются значительные градиенты параметров теплообмена. Значения теплового потока вдоль лобовой поверхности меняются примерно четырёхкратно для равновесного воздуха и трёхкратно — для неравновесного (рис. 8). Абсолютный максимум теплового потока на лобовой поверхности наблюдается в окрестности кромки рядом с критической точкой: 2 200 кВт/м² для равновесного воздуха и 1 550 кВт/м² — для неравновесного.

Учёт неравновесности физикохимических процессов в ударном слое и конечной каталитичности поверхности приводит к уменьшению общего уровня тепловых потоков на лобовой и боковой поверхностях ВА (рис. 7), причём наиболее заметное относительное падение тепловых потоков происходит с наветренной стороны на кромке и сразу после неё на боковой поверхности.

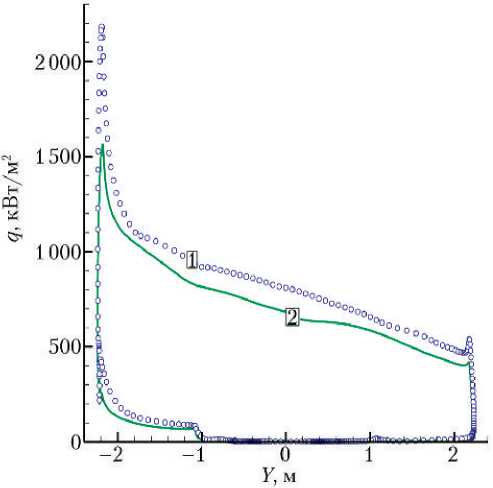
Рис. 7. Тепловой поток

ВА для равновесного (1)

Точка траектории № 2

Qw (кВт/м2) на поверхности и неравновесного (2) воздуха.

Для оценки влияния эффектов не-равновесности на конвективный теплообмен проведён анализ тепловых потоков по траектории спуска в трёх характерных точках поверхности ВА. Схема расположения анализируемых точек показана на рис. 9.

а)

б)

Рис. 8. Коэффициент α /C_p (кг/(м²с)) (а) и равновесная радиационная температура T_w (K) (б) на поверхности ВА для равновесного (1) и неравновесного (2) воздуха. Точка траектории № 2

На рис. 10 приведены зависимости теплового потока q1 для равновесного и неравновесного воздуха в центре лобового щита (точка P1 на рис. 9) от времени полёта. На большой части траектории значения q1 для равновесного и неравновесного воздуха довольно близки, что свидетельствует о том, что состояние газа в ударном слое здесь близко к равновесию. Прослеживается зависимость разницы qнв и qрв от абсолютного значения тепловых потоков, с увеличением температуры и плотности в ударном слое течение становится ближе к равновесию, и различие значений qнв и qрв уменьшается. Максимальное отличие наблюдается на большой высоте (первое погружение) и при умеренной скорости (второе погружение), когда течение становится существенно неравновесным и тепловой поток относительно небольшой.

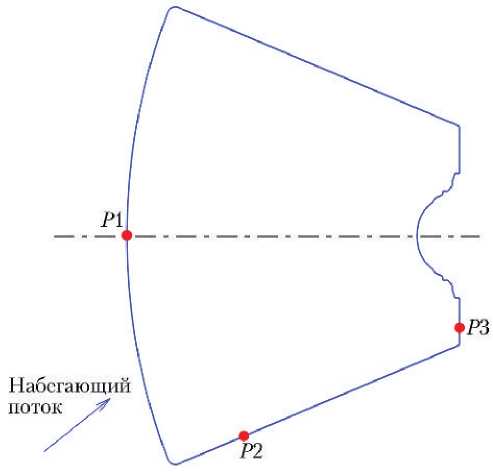
Рис. 9. Схема расположения анализируемых точек на поверхности

Различие значений q _нв и q _рв на боковой и в донной области ВА обусловливается расширением и охлаждением газового потока, химические реакции здесь замедляются (замораживаются), и состояние потока становится далёким от равновесия. Это хорошо видно из сравнения зависимостей конвективного теплового потока q и соответствующего интегрального по траектории теплопри-тока Q от времени полёта в точках P 2 и Р 3 для равновесного и неравновесного воздуха, приведённых на рис. 11. Интегральный теплоприток, рассчитанный по модели неравновесного воздуха, меньше, чем в модели равновесно-диссоциирующего воздуха: для точки P 2 почти в два раза, для точки P 3 — почти в три. Реализовать эффект снижения тепловых потоков на боковой и торцевой поверхностях возможно при применении ТЗП с низкой каталитической активностью при высоких температурах.

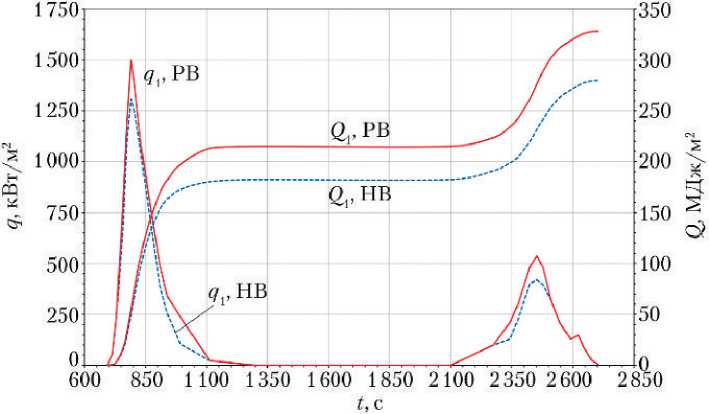
Рис. 10. Конвективный (ламинарно-турбулентный) тепловой поток q и интегральный теплоподвод Q в точке P1. РВ/НВ — равновесный/неравновесный воздух

а)

б)

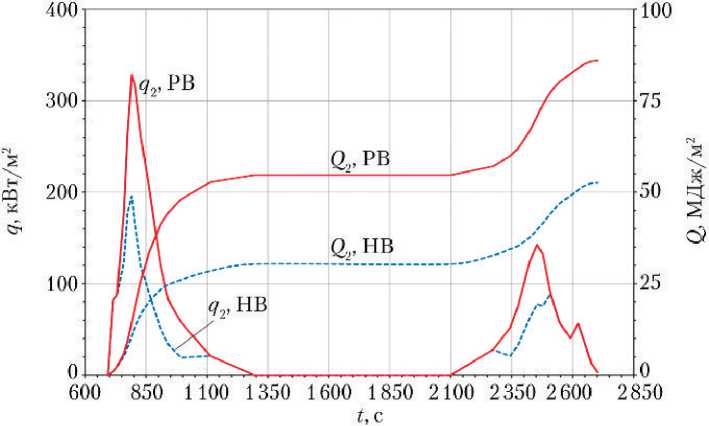
Рис. 11. Конвективный (ламинарно-турбулентный) тепловой поток q и интегральный теплоприток Q в точках Р2(а) и P3(б). РВ/НВ — равновесный/неравно-весный воздух

выводы

Проведённые расчётные исследования показывают, что на всей поверхности ВА, кроме донной части, тепловые потоки, полученные по модели неравновесного воздуха, всегда ниже тепловых потоков, полученных по модели равновесного воздуха.

Вдоль основной части траектории состояние газа в ударном слое на лобовом щите близко к равновесному — тепловые потоки, а также интегральный по траектории теплоприток, при равновесном и неравновесном обтеканиях отличаются на 10–20%. Наиболее заметное относительное падение тепловых потоков происходит с наветренной стороны на кромке и сразу после неё на боковой поверхности. Различие между равновесным и неравновесным случаями увеличивается на большой высоте (первое погружение) и при умеренной скорости (второе погружение), когда течение становится существенно неравновесным, и тепловой поток относительно небольшой.

На боковой поверхности и в донной части ВА на участках аэродинамического нагрева течение всегда неравновесное, что обусловлено расширением и охлаждением газового потока. В результате интегральный по траектории теплоприток для равновесного воздуха превышает значение для неравновесного воздуха в два и три раза на боковой и донной поверхностях, соответственно.

Для рассмотренной траектории использование теплозащитных покрытий с низкой каталитической активностью, работоспособного при высоких температурах, позволяет существенно снизить тепловые потоки на поверхность ВА.